2025-05-22：找到初始输入字符串Ⅱ。用go语言，Alice 在键盘上输入一个字符串，但由于输入时可能按键时间过长，导致某些字符被重复输入多次。

给定一个字符串 word，表示最终显示在屏幕上的内容，同时给定一个正整数 k，表示 Alice 最初打算输入的字符串长度至少为 k。

请你计算，满足这种情况的所有可能的原字符串方案数，并将结果对 1000000007 取模后返回。

1 <= word.length <= 5 * 100000。

word 只包含小写英文字母。

1 <= k <= 2000。

输入：word = “aabbccdd”, k = 7。

输出：5。

解释：

可能的字符串包括：“aabbccdd” ，“aabbccd” ，“aabbcdd” ，“aabccdd” 和 “abbccdd” 。

题目来自力扣3333。

解决步骤

1. 分组连续相同字符：

   • 首先将 word 分成连续的相同字符的组。例如，“aabbccdd” 分为 [“aa”, “bb”, “cc”, “dd”]。
   • 对于每组，至少保留一个字符，因此每组的选择是保留 1 到 count 个字符（count 是该组字符的原始数量）。

2. 计算初始方案数：

   • 对于每组，如果该组的字符数为 c，则可以选择保留 1 到 c 个字符，因此有 c 种选择。
   • 初始方案数是所有组的 c 的乘积。例如，“aa”, “bb”, “cc”, “dd” 的 c 分别为 2, 2, 2, 2，初始方案数为 2 * 2 * 2 * 2 = 16。
   • 但我们需要排除那些原字符串长度小于 k 的情况。

3. 动态规划计算不满足条件的方案数：

   • 我们需要计算原字符串长度小于 k 的方案数，然后用初始方案数减去这些不满足条件的方案数。
   • 设原字符串长度为 total_length，则 total_length 是各组保留字符数的和。
   • 我们需要计算 total_length < k 的方案数。
   • 动态规划：
     • 定义 f[j] 表示选择前 i 组时，总长度为 j 的方案数。
     • 初始时 f[0] = 1（不选任何字符的方案数为 1，但实际每组至少选 1 个字符，因此需要调整）。
     • 对于每组，其字符数为 c，可以选择保留 1 到 c 个字符，因此对动态规划的转移是：
       • 对于每个 j，f[j] 可以从 f[j - 1], f[j - 2], …, f[j - c] 转移而来。
     • 由于每组至少选 1 个字符，因此实际的总长度至少是组的数量（即 m，组数）。
     • 我们需要计算 m <= total_length < k 的方案数。
   • 具体实现中，可以优化空间复杂度为 O(k)。

4. 排除不满足条件的方案数：

   • 初始方案数为 ans。
   • 不满足条件的方案数为 sum(f[m..k-1])。
   • 最终结果为 ans - sum(f[m..k-1])。

时间复杂度

1. 分组连续相同字符：O(n)，其中 n 是 word 的长度。
2. 计算初始方案数：O(m)，其中 m 是组的数量。
3. 动态规划：
   • 外层循环遍历所有组：O(m)。
   • 内层循环更新动态规划数组：O(k)。
   • 总时间复杂度：O(m * k)。
   • 由于 m <= n 且 k <= 2000，因此动态规划部分的时间复杂度为 O(n * k)。
4. 总时间复杂度：O(n * k)。

空间复杂度

1. 分组存储：O(m)，但可以优化为 O(1)（无需显式存储所有组）。
2. 动态规划数组：O(k)。
3. 总空间复杂度：O(k)。

总结

• 总时间复杂度：O(n * k)。
• 总额外空间复杂度：O(k)。

Go完整代码如下：

`

package main

import (
	"fmt"
)

func possibleStringCount(word string, k int) int {
	if len(word) < k { // 无法满足要求
		return 0
	}

	const mod = 1_000_000_007
	cnts := []int{}
	ans := 1
	cnt := 0
	for i := range word {
		cnt++
		if i == len(word)-1 || word[i] != word[i+1] {
			// 如果 cnt = 1，这组字符串必选，无需参与计算
			if cnt > 1 {
				if k > 0 { // 保证空间复杂度为 O(k)
					cnts = append(cnts, cnt-1)
				}
				ans = ans * cnt % mod
			}
			k-- // 注意这里把 k 减小了
			cnt = 0
		}
	}

	if k <= 0 {
		return ans
	}

	f := make([]int, k)
	f[0] = 1
	for _, c := range cnts {
		// 原地计算 f 的前缀和
		for j := 1; j < k; j++ {
			f[j] = (f[j] + f[j-1]) % mod
		}
		// 计算子数组和
		for j := k - 1; j > c; j-- {
			f[j] -= f[j-c-1]
		}
	}

	for _, x := range f {
		ans -= x
	}
	return (ans%mod + mod) % mod // 保证结果非负
}

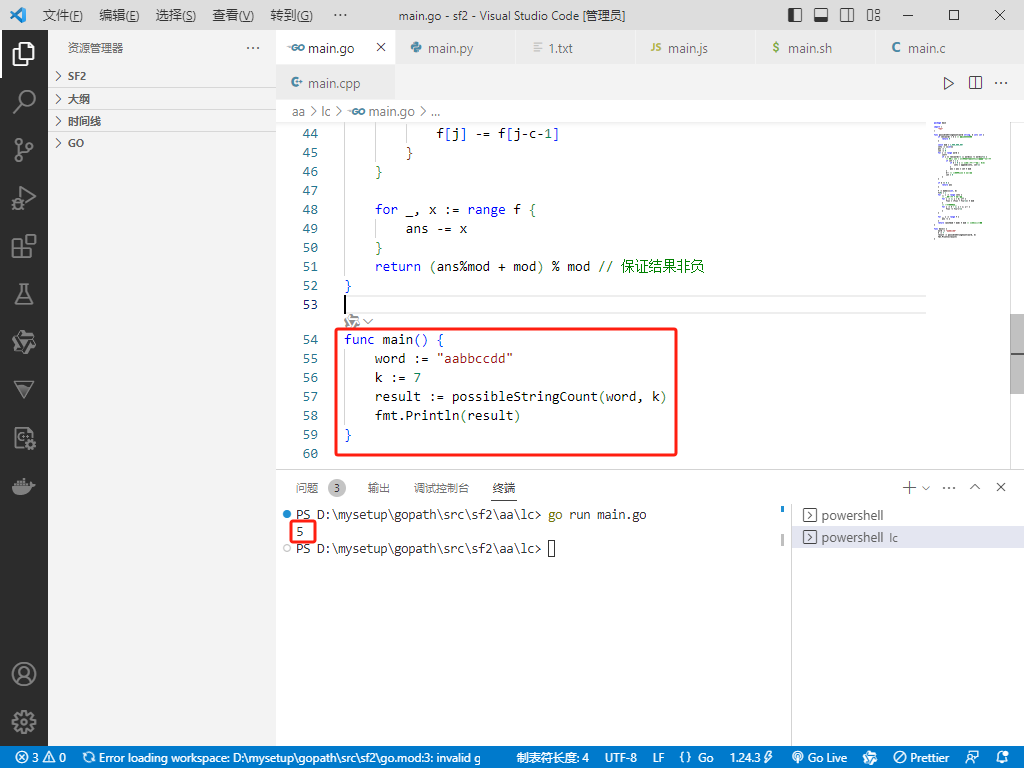
func main() {
	word := "aabbccdd"
	k := 7
	result := possibleStringCount(word, k)
	fmt.Println(result)
}

Rust完整代码如下：

`

fn possible_string_count(word: &str, k: usize) -> i32 {
    let mod_val = 1_000_000_007i64;
    let n = word.len();
    if n < k {
        return 0;
    }

    let bytes = word.as_bytes();
    let mut cnts = vec![];
    let mut ans = 1i64;
    let mut cnt = 0usize;
    let mut kk = k as i32;

    for i in 0..n {
        cnt += 1;
        if i == n - 1 || bytes[i] != bytes[i + 1] {
            if cnt > 1 {
                if kk > 0 {
                    cnts.push(cnt - 1);
                }
                ans = ans * (cnt as i64) % mod_val;
            }
            kk -= 1;
            cnt = 0;
        }
    }

    if kk <= 0 {
        return (ans % mod_val) as i32;
    }

    let k = kk as usize;
    let mut f = vec![0i64; k];
    f[0] = 1;

    for &c in &cnts {
        // 计算前缀和
        for j in 1..k {
            f[j] = (f[j] + f[j - 1]) % mod_val;
        }
        // 计算子数组和
        for j in (c + 1..k).rev() {
            f[j] = (f[j] - f[j - c - 1] + mod_val) % mod_val;
        }
    }

    for &x in &f {
        ans = (ans - x + mod_val) % mod_val;
    }

    ans as i32
}

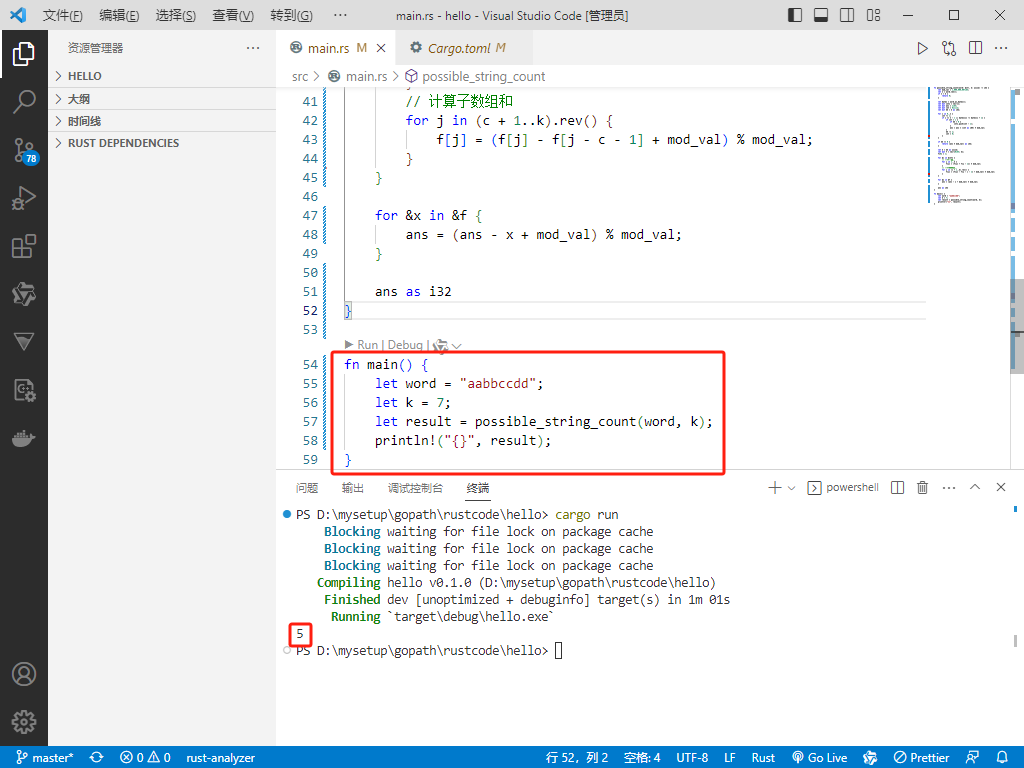
fn main() {
    let word = "aabbccdd";
    let k = 7;
    let result = possible_string_count(word, k);
    println!("{}", result);
}