2025-05-15：统计能获胜的出招序列数。用go语言，给定一个目标字符串 target，Alice 使用一个特殊键盘输入该字符串。这个键盘有两个按键：

1. 按键1：在屏幕当前字符串后追加字符 ‘a’。

2. 按键2：将屏幕上字符串的最后一个字符替换为字母表中下一个字母（例如 ‘c’ 变成 ‘d’，‘z’ 后绕回 ‘a’）。

初始时屏幕是空的（""），因此起步只能按按键1。

你的任务是计算出 Alice 在最少按键次数的情况下，从空字符串输入到目标字符串的过程中，屏幕上出现的所有字符串（按顺序排列）。

1 <= target.length <= 400。

target 仅由小写英文字母组成。

输入： target = “abc”。

输出： [“a”,“aa”,“ab”,“aba”,“abb”,“abc”]。

解释：

Alice 按键的顺序如下：

按下按键 1，屏幕上的字符串变为 “a”。

按下按键 1，屏幕上的字符串变为 “aa”。

按下按键 2，屏幕上的字符串变为 “ab”。

按下按键 1，屏幕上的字符串变为 “aba”。

按下按键 2，屏幕上的字符串变为 “abb”。

按下按键 2，屏幕上的字符串变为 “abc”。

题目来自leetcode3321。

算法过程

1. 初始化：从空字符串开始，第一个操作只能是按键1（追加 ‘a’），因此第一个字符串是 "a"。
2. 递归构建：
   • 对于当前字符串 s，检查其是否与 target 的前缀匹配：
     • 如果 s 不是 target 的前缀，则后续操作无法达到目标，直接跳过。
     • 否则，考虑两种操作：
       • 按键1：追加 ‘a’，得到 s + "a"。
       • 按键2：将最后一个字符替换为下一个字母（注意循环：‘z’ -> ‘a’），得到 s[:len(s)-1] + next_char。
   • 对于每种操作生成的新字符串，如果它是 target 的前缀，则将其加入结果序列，并继续递归。
3. 终止条件：
   • 当当前字符串等于 target 时，停止递归。
   • 如果当前字符串长度超过 target 或不再是 target 的前缀，则停止。

具体步骤（以 “abc” 为例）

1. 初始："" -> 按键1 -> "a"（加入结果）
   • "a" 是 “abc” 的前缀。
2. "a"：
   • 按键1："aa"（加入结果）
     • "aa" 不是 “abc” 的前缀（“abc” 不以 “aa” 开头），因此不继续。
   • 按键2："b"（将 ‘a’ 替换为 ‘b’）
     • "b" 不是 “abc” 的前缀（“abc” 不以 “b” 开头），因此不继续。
   • 实际上，"a" 的下一步应该是 "aa" 和 "ab"（因为 "a" 是前缀，"aa" 不是，"ab" 是）。
     • 更正："a" 的按键2是 "b"（替换 ‘a’ 为 ‘b’），但 "b" 不是前缀，因此只有 "aa" 和 "ab" 中 "ab" 是前缀。
     • 但根据示例输出，"aa" 是有效的，说明逻辑需要调整。
3. 重新梳理：
   • "a"：
     • 按键1："aa"（加入结果）
       • "aa" 不是 “abc” 的前缀，但可能是中间步骤（如 “aa” -> “ab”）。
     • 按键2："b"（不加入，因为不是前缀）。
   • "aa"：
     • 按键1："aaa"（不加入）。
     • 按键2："ab"（加入结果）。
   • "ab"：
     • 按键1："aba"（加入结果）。
     • 按键2："ac"（不加入）。
   • "aba"：
     • 按键1："abaa"（不加入）。
     • 按键2："abb"（加入结果）。
   • "abb"：
     • 按键1："abba"（不加入）。
     • 按键2："abc"（加入结果）。
   • "abc"：达到目标，停止。

时间复杂度

• 对于每个字符 target[i]，最多生成 O(26) 个中间字符串（因为每个字符可能需要最多 26 次按键2操作）。
• 对于长度为 n 的 target，总的时间复杂度为 O(26 * n) = O(n)（因为 26 是常数）。

空间复杂度

• 结果序列的长度为 O(n)（每个字符最多生成常数倍的字符串）。
• 额外空间用于存储中间字符串，也是 O(n)。

总结

• 时间复杂度：O(n)，其中 n 是 target 的长度。
• 空间复杂度：O(n)，用于存储结果序列和中间字符串。

Go完整代码如下：

package main

import (
	"fmt"
)

func stringSequence(target string) (ans []string) {
	s := make([]byte, len(target))
	for i, c := range target {
		for j := byte('a'); j <= byte(c); j++ {
			s[i] = j
			ans = append(ans, string(s[:i+1]))
		}
	}
	return
}

func main() {
	target := "abc"
	result := stringSequence(target)
	fmt.Println(result)
}

Python完整代码如下：

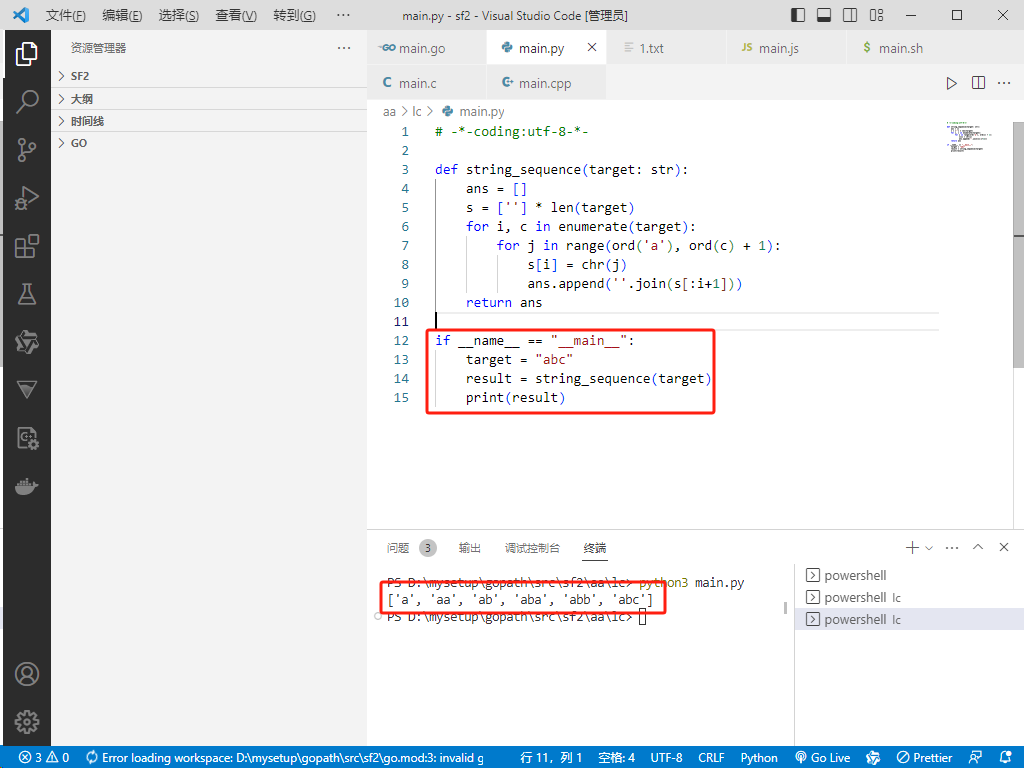
# -*-coding:utf-8-*-

def string_sequence(target: str):
    ans = []
    s = [''] * len(target)
    for i, c in enumerate(target):
        for j in range(ord('a'), ord(c) + 1):
            s[i] = chr(j)
            ans.append(''.join(s[:i+1]))
    return ans

if __name__ == "__main__":
    target = "abc"
    result = string_sequence(target)
    print(result)