2025-04-17:穿越网格图的安全路径。用go语言,给定一个大小为 m 行 n 列的二维二进制数组 grid,以及一个初始健
【摘要】 2025-04-17:穿越网格图的安全路径。用go语言,给定一个大小为 m 行 n 列的二维二进制数组 grid,以及一个初始健康值 health。你从左上角的位置 (0, 0) 出发,目标是抵达右下角的位置 (m - 1, n - 1)。在移动时,你可以选择上下左右四个方向的相邻格子,但前提是移动后你的健康值始终保持大于0。如果你进入的格子 grid[i][j] 为 1,则表示该格子存在危...
2025-04-17:穿越网格图的安全路径。用go语言,给定一个大小为 m 行 n 列的二维二进制数组 grid,以及一个初始健康值 health。
你从左上角的位置 (0, 0) 出发,目标是抵达右下角的位置 (m - 1, n - 1)。
在移动时,你可以选择上下左右四个方向的相邻格子,但前提是移动后你的健康值始终保持大于0。
如果你进入的格子 grid[i][j] 为 1,则表示该格子存在危险,会减少你当前的健康值 1 点。
请判断是否存在一条路径,使你能够从起点走到终点且在终点时健康值仍然是正数。
如果可以达到,返回 true,否则返回 false。
m == grid.length。
n == grid[i].length。
1 <= m, n <= 50。
2 <= m * n。
1 <= health <= m + n。
grid[i][j] 要么是 0 ,要么是 1 。
输入:grid = [[0,1,0,0,0],[0,1,0,1,0],[0,0,0,1,0]], health = 1 。
输出:true 。
解释:
沿着下图中灰色格子走,可以安全到达最终的格子。
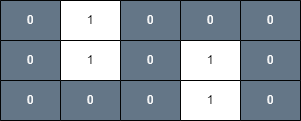
题目来自leetcode3286。
分步骤的过程描述
-
初始状态准备
- 获取网格的行数 m 和列数 n。
- 创建一个二维数组
dis,用于记录从起点 (0,0) 到每个位置所消耗的最少健康值(即走过的格子中“1”的数量)。 - 初始化所有
dis值为极大数(表示未访问或尚无更优路径)。 - 起点 (0,0) 的
dis初始化为grid[0][0](因为开始位置如果是“1”,健康值就先减1)。
-
方向定向
- 定义四个可能的移动方向:上、下、左、右。
-
队列初始化(0-1 BFS思想)
- 使用两个队列(一组双端队列结构)分别存储开销为0的节点和开销为1的节点,目的是实现一种类似0-1 BFS的算法,用来优先扩展无额外健康损耗的路径。
- 将起点放入对应开销的队列中。
-
主循环遍历
- 只要两个队列中任意一个非空,循环继续。
- 优先从开销为0的队列取出当前节点处理,如果没有,则从开销为1的队列中取一个节点。
- 取出节点后,检查当前位置累计的健康损耗值是否已经达到或超过给定的健康值
health,如果达到及以上,直接跳过(因为健康值已经不够,不能继续走这条路径)。 - 若当前位置是终点 (m-1, n-1),且累计的健康损耗未超过限制,表示找到了一条可行路径,直接返回
true。
-
邻居扩展
- 对当前位置的四个相邻格子进行遍历。
- 对于每个合法(在网格范围内)的邻居,计算从起点到该邻居的健康损耗:当前节点损耗 + 邻居格子的值(0或1)。
- 如果计算得到的损耗小于该邻居之前记录的最小损耗,则更新该邻居的健康损耗值,并放入对应的队列(开销0或1队列)中,以便后续按照优先级扩展。
-
循环终止条件
- 如果循环结束还没有返回
true,说明没有找到满足健康值条件的路径,返回false。
- 如果循环结束还没有返回
总体时间复杂度分析
- 搜索会遍历所有格子最多一次或多次,每个格子最多被更新的次数取决于路径更新次数。
- 使用 0-1 BFS 的思想,使得每条边边权只有 0 或 1,故整体执行效率接近于 BFS,时间复杂度为 O(m * n)。
- 每个节点最多被入队和出队若干次,但由于使用
dis数组来避免多余的更新,减少了重复搜索。
总体空间复杂度分析
- 需要一个
dis二维数组记录状态,大小为 m * n,空间是 O(m * n)。 - 队列(双端队列)存储节点,最坏情况下也存储所有节点,空间复杂度为 O(m * n)。
- 额外常数空间用于方向数组和少量变量,忽略不计。
综上,总的时间复杂度和空间复杂度均为 O(m * n)。
Go完整代码如下:
package main
import (
"fmt"
"math"
)
func findSafeWalk(grid [][]int, health int) bool {
type pair struct{ x, y int }
dirs := []pair{{0, -1}, {0, 1}, {-1, 0}, {1, 0}}
m, n := len(grid), len(grid[0])
dis := make([][]int, m)
for i := range dis {
dis[i] = make([]int, n)
for j := range dis[i] {
dis[i][j] = math.MaxInt
}
}
dis[0][0] = grid[0][0]
q := [2][]pair{{{}}} // 两个 slice 头对头来实现 deque
for {
var p pair
if len(q[0]) > 0 {
p, q[0] = q[0][len(q[0])-1], q[0][:len(q[0])-1]
} else {
p, q[1] = q[1][0], q[1][1:]
}
i, j := p.x, p.y
if dis[i][j] >= health {
return false
}
if i == m-1 && j == n-1 {
return true
}
for _, d := range dirs {
x, y := i+d.x, j+d.y
if 0 <= x && x < m && 0 <= y && y < n {
cost := grid[x][y]
if dis[i][j]+cost < dis[x][y] {
dis[x][y] = dis[i][j] + cost
q[cost] = append(q[cost], pair{x, y})
}
}
}
}
}
func main() {
grid := [][]int{{0,1,0,0,0},{0,1,0,1,0},{0,0,0,1,0}}
health := 1
results := findSafeWalk(grid, health)
fmt.Println(results)
}
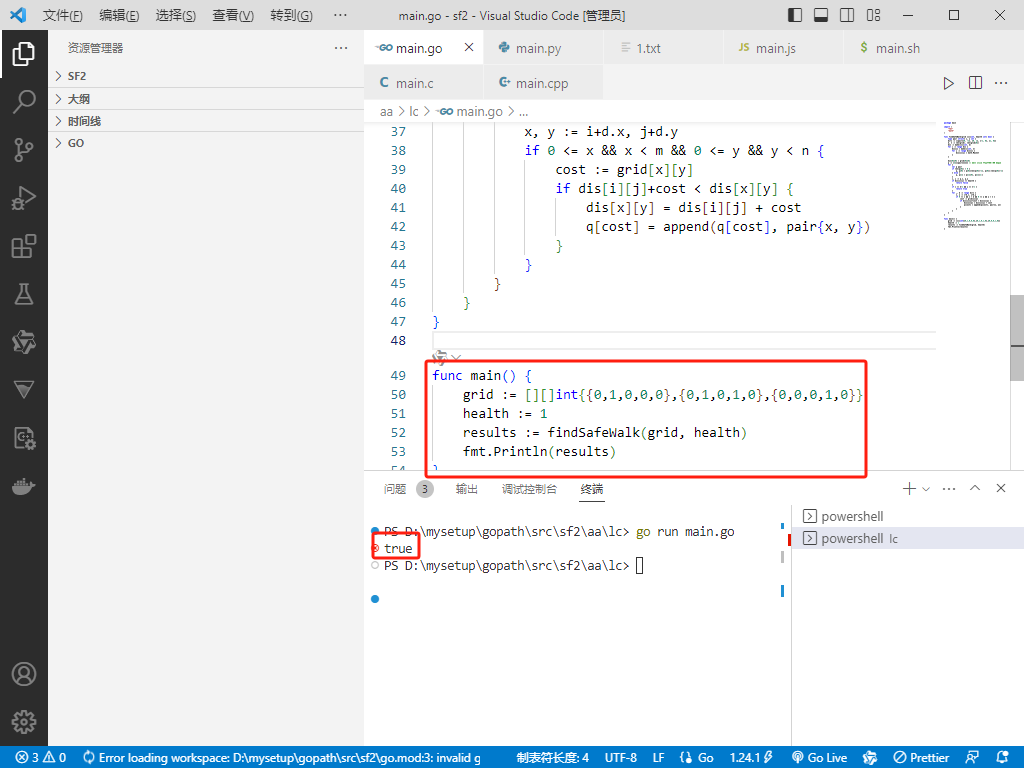
Python完整代码如下:
# -*-coding:utf-8-*-
from collections import deque
import sys
def find_safe_walk(grid, health):
dirs = [(0, -1), (0, 1), (-1, 0), (1, 0)]
m, n = len(grid), len(grid[0])
dis = [[sys.maxsize] * n for _ in range(m)]
dis[0][0] = grid[0][0]
# 使用两个双端队列模拟0-1 BFS的deque
q = [deque(), deque()]
q[dis[0][0]].append((0, 0))
while q[0] or q[1]:
if q[0]:
i, j = q[0].pop()
else:
i, j = q[1].popleft()
if dis[i][j] >= health:
return False
if i == m - 1 and j == n - 1:
return True
for dx, dy in dirs:
x, y = i + dx, j + dy
if 0 <= x < m and 0 <= y < n:
cost = grid[x][y]
if dis[i][j] + cost < dis[x][y]:
dis[x][y] = dis[i][j] + cost
q[cost].append((x, y))
return False
if __name__ == "__main__":
grid = [
[0,1,0,0,0],
[0,1,0,1,0],
[0,0,0,1,0],
]
health = 1
result = find_safe_walk(grid, health)
print(result)
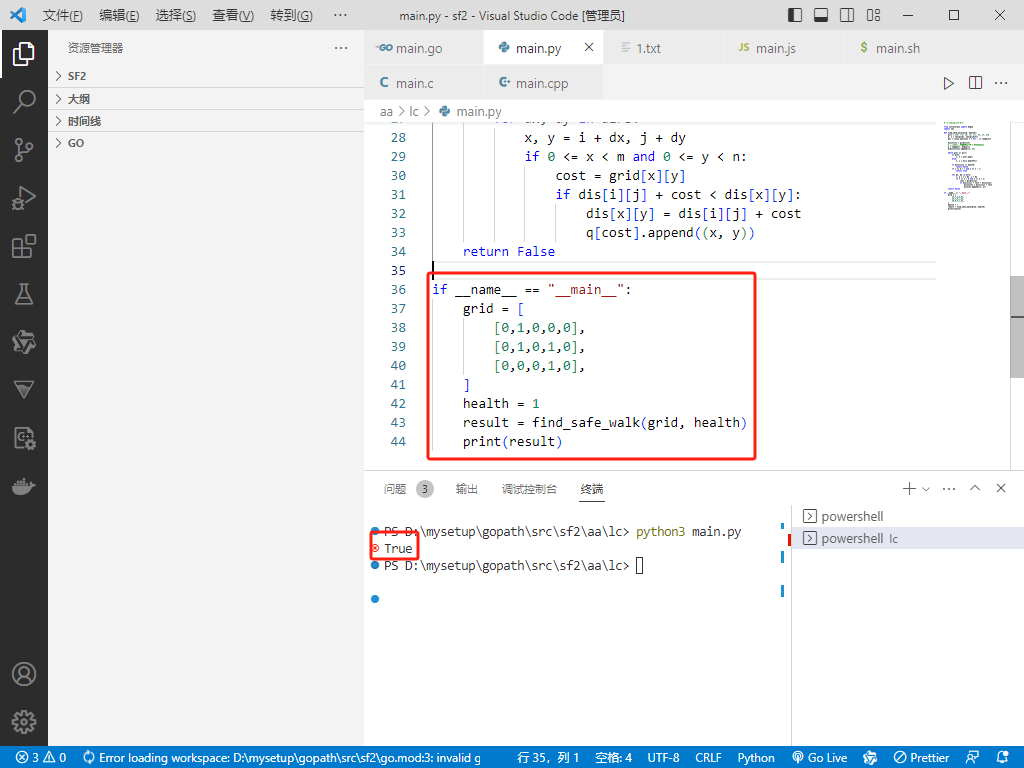
【声明】本内容来自华为云开发者社区博主,不代表华为云及华为云开发者社区的观点和立场。转载时必须标注文章的来源(华为云社区)、文章链接、文章作者等基本信息,否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)