2025-04-09：第 K 近障碍物查询。用go语言，我们有一个无限大的二维平面。给定一个正整数 k 和一个二维数组 queries，每个元素 queries[i] = [x, y] 表示在平面上的坐标 (x, y) 处建立一个障碍物。系统保证在之前的查询中不会在同一坐标位置再建立障碍物。

在每次建立障碍物后，我们需要找出距离原点最近的 k 个障碍物的距离，并返回第 k 个障碍物距离原点的距离。如果当前障碍物数量少于 k 个，则返回 -1。

距离的计算方式为曼哈顿距离，即距离原点的距离定义为 |x| + |y|。请返回一个整数数组 results，其中 results[i] 表示在第 i 次建立障碍物后、距离原点第 k 近的障碍物距离原点的距离。

1 <= queries.length <= 2 * 100000。

所有 queries[i] 互不相同。

-109 <= queries[i][0], queries[i][1] <= 1000000000。

1 <= k <= 100000。

输入：queries = [[1,2],[3,4],[2,3],[-3,0]], k = 2。

输出：[-1,7,5,3]。

解释：

最初，不存在障碍物。

queries[0] 之后，少于 2 个障碍物。

queries[1] 之后， 两个障碍物距离原点的距离分别为 3 和 7 。

queries[2] 之后，障碍物距离原点的距离分别为 3 ，5 和 7 。

queries[3] 之后，障碍物距离原点的距离分别为 3，3，5 和 7 。

题目来自leetcode3275。

步骤描述

1. 初始化过程：

   • 创建一个 results 数组，用于存储每次查询后第 k 个最近障碍物的距离，如果障碍物不足 k 个，则存储 -1。
   • 创建一个优先队列 pq，这个队列实现为一个大根堆（最大堆），用于存储到原点的曼哈顿距离。

2. 处理每个查询：

   • 遍历每个查询 queries，每个查询都包含一个障碍物的位置 [x, y]。
   • 计算当前障碍物的曼哈顿距离 dist，公式为：abs(x) + abs(y)。

3. 将距离加入优先队列：

   • 使用 heap.Push 将当前障碍物的距离 dist 加入到优先队列 pq 中。

4. 管理堆的大小：

   • 检查优先队列的大小是否超过 k。如果超过，使用 heap.Pop 将堆顶元素移除，以确保堆中最多只有 k 个元素。

5. 记录结果：

   • 如果当前优先队列的长度等于 k，说明当前已经有 k 个障碍物，那么可以安全地获取当前第 k 近的障碍物的距离，存入 results 数组中。由于是大根堆，第 k 个障碍物的距离是堆中的最大元素，因此取 (*pq)[0]。

6. 返回最终结果：

   • 在遍历完成后，返回 results 数组，结果即为每个查询后第 k 个最近障碍物的距离。

时间复杂度分析

• 对于每个查询，可能需要将一个新元素插入到优先队列中，这个操作的时间复杂度是 O(log k)。在处理的过程中，如果优先队列的大小超过 k，需要再进行一次弹出操作，这也是 O(log k) 的复杂度。
• 因此，对于 n 个查询，总的时间复杂度为 O(n log k)。

空间复杂度分析

• 优先队列在最坏情况下会存储 k 个元素，因此额外的空间复杂度为 O(k)。
• 结果数组 results 大小为 n，因此总的空间复杂度是 O(n + k)，但是通常只关注更大的量，所以可以认为额外的空间复杂度是 O(k)。

总结

• 时间复杂度：O(n log k)
• 额外空间复杂度：O(k)

Go完整代码如下：

package main

import (
	"container/heap"
	"fmt"
)

// 定义一个优先队列结构体
type IntHeap []int

// 实现 Heap 接口的方法
func (h IntHeap) Len() int           { return len(h) }
func (h IntHeap) Less(i, j int) bool { return h[i] > h[j] } // 大根堆
func (h IntHeap) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }

func (h *IntHeap) Push(x interface{}) {
	*h = append(*h, x.(int))
}

func (h *IntHeap) Pop() interface{} {
	old := *h
	n := len(old)
	x := old[n-1]
	*h = old[0 : n-1]
	return x
}

// 主函数
func resultsArray(queries [][]int, k int) []int {
	n := len(queries)
	res := make([]int, n)
	for i := range res {
		res[i] = -1
	}

	pq := &IntHeap{}
	heap.Init(pq) // 初始化优先队列

	for i, query := range queries {
		x := query[0]
		y := query[1]
		dist := abs(x) + abs(y)

		heap.Push(pq, dist) // 将当前障碍物距离加入队列

		if pq.Len() > k {
			heap.Pop(pq) // 保持队列大小不超过 k
		}

		if pq.Len() == k {
			res[i] = (*pq)[0] // 当前第 k 个障碍物的距离
		}
	}
	return res
}

func abs(x int) int {
	if x < 0 {
		return -x
	}
	return x
}

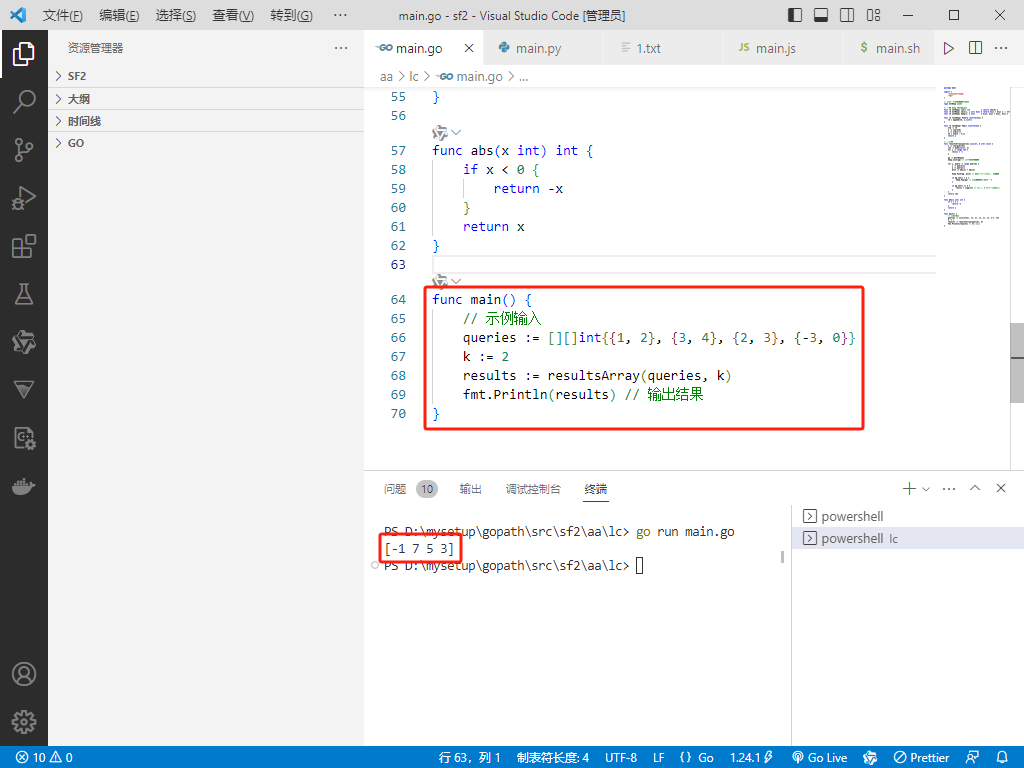
func main() {
	// 示例输入
	queries := [][]int{{1, 2}, {3, 4}, {2, 3}, {-3, 0}}
	k := 2
	results := resultsArray(queries, k)
	fmt.Println(results) // 输出结果
}

Python完整代码如下：

# -*-coding:utf-8-*-

import heapq

def results_array(queries, k):
    n = len(queries)
    res = [-1] * n
    pq = []  # 用于优先队列

    for i, query in enumerate(queries):
        x, y = query
        dist = abs(x) + abs(y)

        heapq.heappush(pq, -dist)  # 使用负值实现大根堆

        if len(pq) > k:
            heapq.heappop(pq)  # 保持队列大小不超过 k

        if len(pq) == k:
            res[i] = -pq[0]  # 当前第 k 个障碍物的距离

    return res

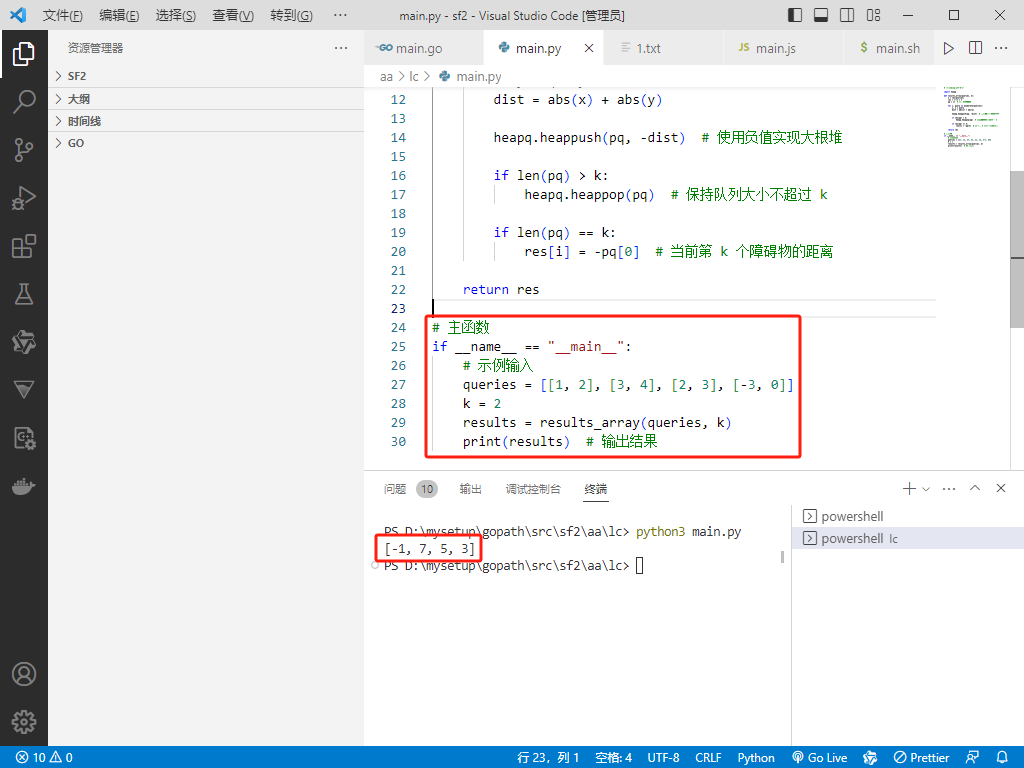
# 主函数
if __name__ == "__main__":
    # 示例输入
    queries = [[1, 2], [3, 4], [2, 3], [-3, 0]]
    k = 2
    results = results_array(queries, k)
    print(results)  # 输出结果