2025-03-25：长度为 K 的子数组的能量值Ⅱ。用go语言，给定一个长度为 n 的整数数组 nums 和一个正整数 k，你需要计算每个长度为 k 的子数组的能量值。

能量值的定义如下：

1.如果子数组中的元素是连续递增的（即 nums[i] + 1 = nums[i + 1] 对于所有有效的 i），那么能量值为该子数组中的最大元素。

2.如果不是连续递增，则能量值为 -1。

你的任务是返回一个长度为 n - k + 1 的数组 results，数组中的每个元素 results[i] 对应于子数组 nums[i…(i + k - 1)] 的能量值。

1 <= n == nums.length <= 100000。

1 <= nums[i] <= 1000000。

1 <= k <= n。

输入：nums = [1,2,3,4,3,2,5], k = 3。

输出：[3,4,-1,-1,-1]。

解释：

nums 中总共有 5 个长度为 3 的子数组：

[1, 2, 3] 中最大元素为 3 。

[2, 3, 4] 中最大元素为 4 。

[3, 4, 3] 中元素 不是 连续的。

[4, 3, 2] 中元素 不是 上升的。

[3, 2, 5] 中元素 不是 连续的。

题目来自leetcode3255。

大体步骤如下：

1. 首先，在 resultsArray 函数中，将传入的整数数组 nums 和正整数 k，以及数组的长度 n 分别存储起来。

2. 创建一个计数器 cnt 用于记录连续递增的元素个数，并初始化为 0。然后创建一个空数组 ans，该数组长度为 n-k+1，用于存储最后的结果。

3. 遍历整数数组 nums，在循环中判断当前元素与前一个元素的关系，以确定能量值的类型。如果当前元素是数组的第一个元素，或者当前元素与前一个元素不相邻，则将计数器 cnt 设置为 1；否则递增计数器 cnt。

4. 如果计数器 cnt 大于等于 k，说明找到了一个长度为 k 的连续递增子数组，此时将该子数组的最大元素存储到结果数组 ans 中的相应位置。

5. 如果计数器 cnt 小于 k，说明未达到要求的连续递增元素个数，这时需要判断当前子数组的起始位置是否在有效范围内（即超过了 k-1 个元素），如果在有效范围内则将该位置处的结果设为 -1。

6. 最后返回得到的结果数组 ans。

总的时间复杂度：

• 遍历整数数组 nums：O(n)，n 为数组的长度。

• 在遍历过程中，每个元素最多会被访问两次，没有嵌套循环，因此时间复杂度为 O(n)。

总的额外空间复杂度：

• 创建了一个大小为 n-k+1 的数组 ans 用于存储最后的结果，所以额外空间复杂度为 O(n-k+1) ≈ O(n)。

Go完整代码如下：

package main

import (
	"fmt"
)

func resultsArray(nums []int, k int) []int {
	n := len(nums)
	cnt := 0
	ans := make([]int, n-k+1)
	for i := 0; i < n; i++ {
		if i == 0 || nums[i]-nums[i-1] != 1 {
			cnt = 1
		} else {
			cnt++
		}
		if cnt >= k {
			ans[i-k+1] = nums[i]
		} else if i-k+1 >= 0 {
			ans[i-k+1] = -1
		}
	}
	return ans
}

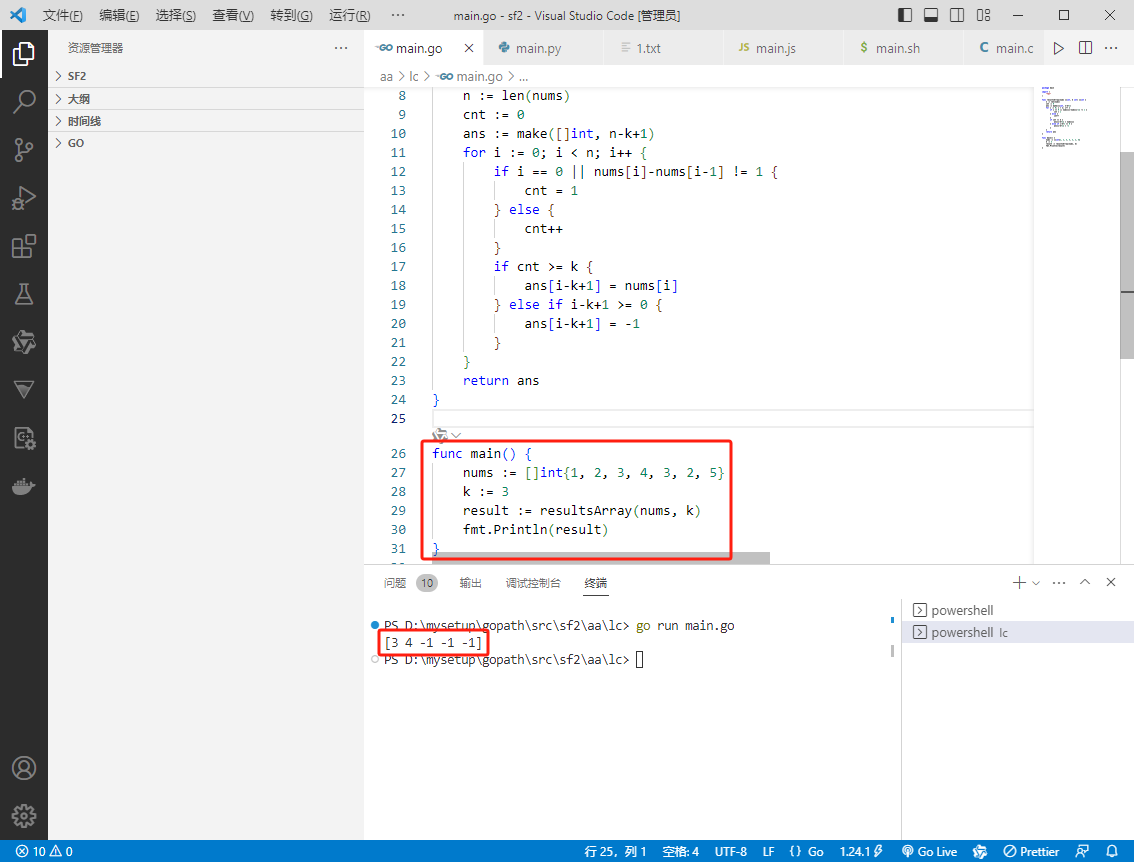
func main() {
	nums := []int{1, 2, 3, 4, 3, 2, 5}
	k := 3
	result := resultsArray(nums, k)
	fmt.Println(result)
}

Python完整代码如下：

# -*-coding:utf-8-*-

def results_array(nums, k):
    n = len(nums)
    cnt = 0
    ans = [-1] * (n - k + 1)

    for i in range(n):
        if i == 0 or nums[i] - nums[i - 1] != 1:
            cnt = 1
        else:
            cnt += 1

        if cnt >= k:
            ans[i - k + 1] = nums[i]
        elif i - k + 1 >= 0:
            ans[i - k + 1] = -1

    return ans

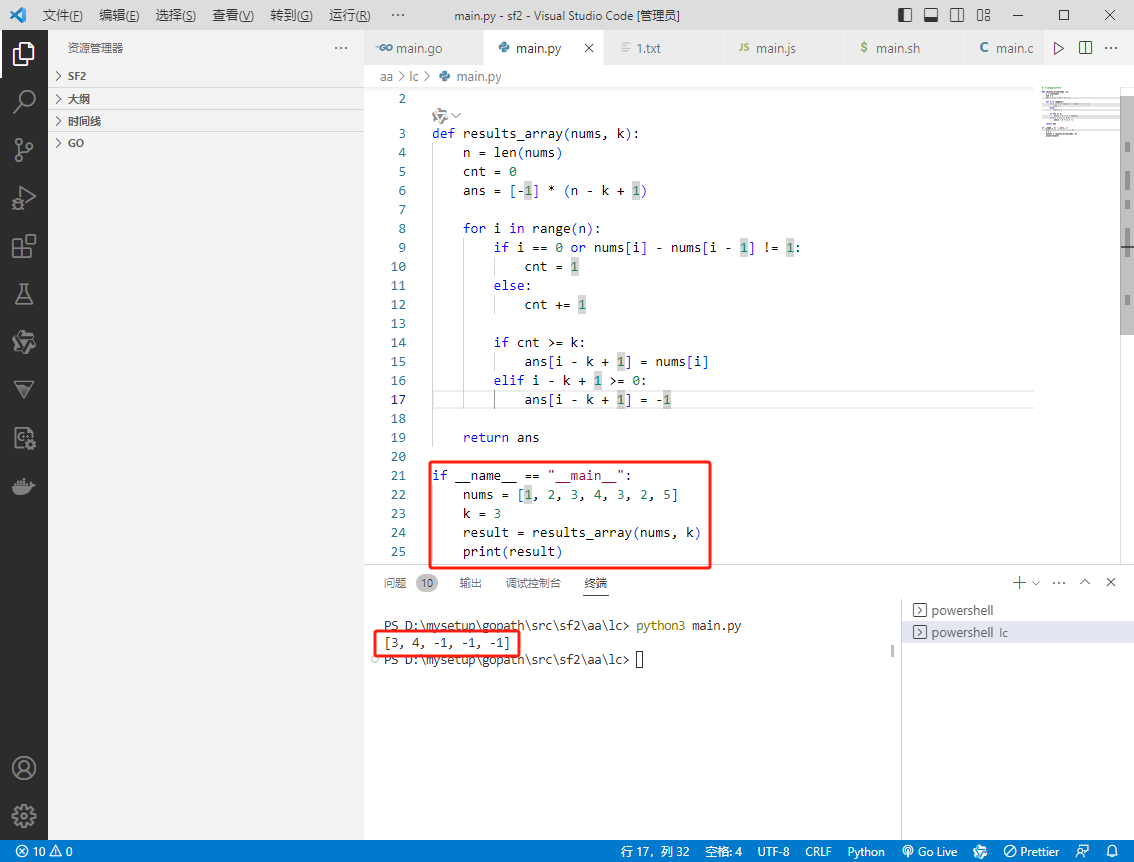
if __name__ == "__main__":
    nums = [1, 2, 3, 4, 3, 2, 5]
    k = 3
    result = results_array(nums, k)
    print(result)