2025-03-21：统计好节点的数目。用go语言，给定一棵无向树，树中有 n 个节点，节点的标号从 0 到 n - 1，根节点为 0。我们有一个长度为 n - 1 的二维数组 edges，其中 edges[i] = [ai, bi] 表示节点 ai 和节点 bi 之间有一条边。

如果一个节点的所有子节点所构成的子树中，包含的节点数都相同，则该节点被称为“好节点”。
你的任务是计算出在这棵树中有多少个“好节点”。

2 <= n <= 100000。

edges.length == n - 1。

edges[i].length == 2。

0 <= ai, bi < n。

输入确保 edges 总表示一棵有效的树。

输入：edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]。

输出：7。

解释：

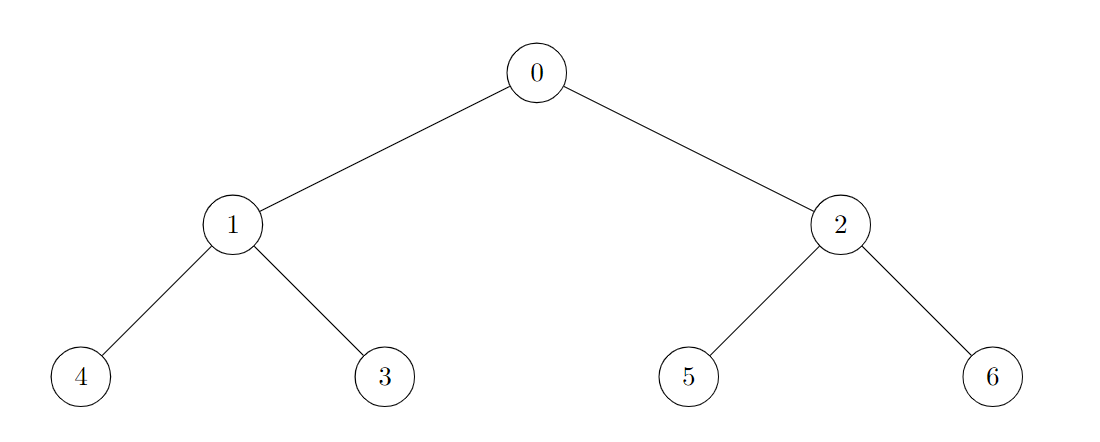
树中的节点都是好节点。

题目来自leetcode3249。

大体步骤如下：

1.首先定义了一个 countGoodNodes 函数，接收一个二维数组 edges，表示树的边的关系。

2.初始化树的节点个数 n 为 len(edges) + 1，创建一个二维数组 g 用来表示节点之间的关系。

3.构建图的邻接表 g，将节点之间的连接关系存储在邻接表中。

4.初始化变量 res 用来统计“好节点”数量。

5.定义一个内部递归函数 dfs，用来遍历节点并统计每个节点的子树大小。

6.在 dfs 函数中，遍历当前节点的子节点，通过递归调用 dfs 函数计算子节点的大小，并判断子节点所构成的子树节点数是否相同。

7.如果子节点构成的子树节点数相同，则将当前节点标记为“好节点”，统计“好节点”的数量。

8.递归遍历整棵树，从根节点开始。

9.在 main 函数中构造示例输入 edges 作为树的边的关系，调用 countGoodNodes 函数计算“好节点”数量，并打印结果。

总的时间复杂度：

• 因为每个节点仅遍历一次，所以遍历整棵树的时间复杂度为 O(n)，其中 n 为节点的数量。

• 在 dfs 函数中，对每个节点的子节点进行遍历，时间复杂度也为 O(n)。

• 因此，总的时间复杂度为 O(n)。

总的额外空间复杂度：

• 使用了邻接表 g 来存储节点之间的关系，占用的额外空间为 O(n)。

• 递归调用时会产生递归栈的空间，最坏情况下会达到 O(n)。

• 因此，总的额外空间复杂度约为 O(n)。

Go完整代码如下：

package main

import (
	"fmt"
)

func countGoodNodes(edges [][]int) int {
	n := len(edges) + 1
	g := make([][]int, n)
	for _, edge := range edges {
		x, y := edge[0], edge[1]
		g[x] = append(g[x], y)
		g[y] = append(g[y], x)
	}
	res := 0
	var dfs func(node, parent int) int
	dfs = func(node, parent int) int {
		valid := true
		treeSize := 0
		subTreeSize := 0

		for _, child := range g[node] {
			if child != parent {
				size := dfs(child, node)
				if subTreeSize == 0 {
					subTreeSize = size
				} else if size != subTreeSize {
					valid = false
				}
				treeSize += size
			}
		}
		if valid {
			res++
		}
		return treeSize + 1
	}

	dfs(0, -1)
	return res
}

func main() {
	edges := [][]int{{0, 1}, {0, 2}, {1, 3}, {1, 4}, {2, 5}, {2, 6}}
	result := countGoodNodes(edges)
	fmt.Println(result)
}

Python完整代码如下：

# -*-coding:utf-8-*-

def countGoodNodes(edges):
    n = len(edges) + 1
    g = [[] for _ in range(n)]
    
    for x, y in edges:
        g[x].append(y)
        g[y].append(x)
    
    res = 0

    def dfs(node, parent):
        nonlocal res
        valid = True
        treeSize = 0
        subTreeSize = 0

        for child in g[node]:
            if child != parent:
                size = dfs(child, node)
                if subTreeSize == 0:
                    subTreeSize = size
                elif size != subTreeSize:
                    valid = False
                treeSize += size
        
        if valid:
            res += 1
        
        return treeSize + 1
    
    dfs(0, -1)
    return res


if __name__ == "__main__":
    edges = [[0, 1], [0, 2], [1, 3], [1, 4], [2, 5], [2, 6]]
    result = countGoodNodes(edges)
    print(result)