2025-03-15：判断矩形的两个角落是否可达。用go语言，给定两个正整数 xCorner 和 yCorner，以及一个二维整数数组 circles，表示若干个圆的信息。判断是否存在一条从矩形的左下角到右上角的路径，这条路径完全在矩形内部，不会触碰或经过任何圆的内部和边界，只在起点和终点与矩形接触。如果存在这样的路径返回true，否则返回false。

3 <= xCorner, yCorner <= 1000000000。

1 <= circles.length <= 1000。

circles[i].length == 3。

1 <= xi, yi, ri <= 1000000000。

输入：X = 3, Y = 4, circles = [[2,1,1]]。

输出：true。

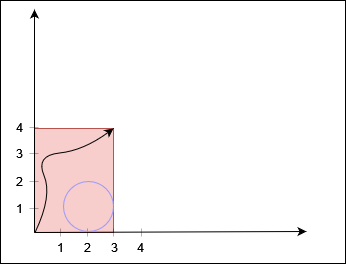
黑色曲线表示一条从 (0, 0) 到 (3, 4) 的路径。

题目来自leetcode3235。

大体步骤如下：

1.定义一个函数 canReachCorner，用于判断矩形的两个角落是否可达。

2.初始化一个记录圆是否被访问过的布尔数组 visited，长度为圆的数量。

3.定义深度优先搜索函数 dfs，用于遍历圆并判断是否存在可达路径。

4.实现函数 pointInCircle，用于判断点是否在圆内部。

5.实现函数 circleIntersectsTopLeftOfRectangle，用于判断圆是否与矩形左上角相交。

6.实现函数 circleIntersectsBottomRightOfRectangle，用于判断圆是否与矩形右下角相交。

7.实现函数 circlesIntersectInRectangle，用于判断两个圆是否在矩形内相交。

8.实现函数 abs，用于求取整数的绝对值。

9.在 main 函数中，给定矩形边界和圆的信息，调用 canReachCorner 函数判断路径是否可达，并输出结果。

总的时间复杂度分析：

• 遍历圆的过程中，需要对每个圆进行判断和搜索，因此最坏情况下时间复杂度为 O(N^2)，其中 N 为圆的数量。

• 在判断点是否在圆内、判断圆与矩形相交等操作中，时间复杂度为 O(1)。

• 因此总的时间复杂度为 O(N^2)，其中 N 为圆的数量。

总的额外空间复杂度分析：

• 程序中额外使用了 visited 数组来记录圆是否被访问过，其大小与圆的数量成正比，因此额外空间复杂度为 O(N)，其中 N 为圆的数量。

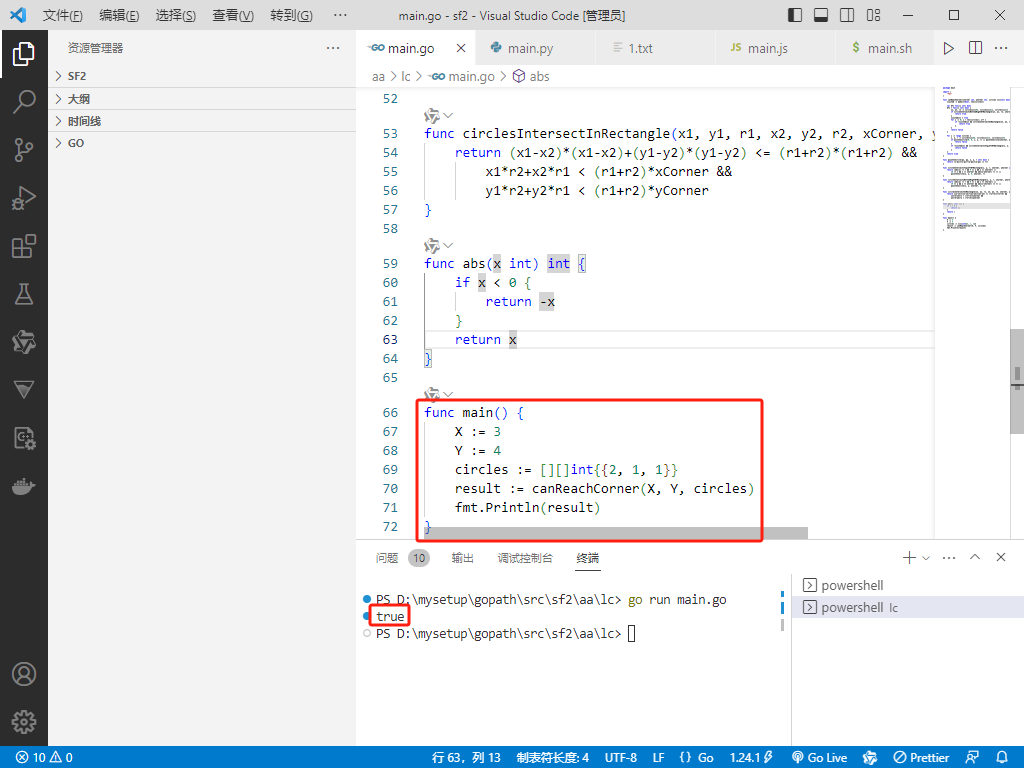
Go完整代码如下：

package main

import (
	"fmt"
)

func canReachCorner(xCorner int, yCorner int, circles [][]int) bool {
	visited := make([]bool, len(circles))

	var dfs func(i int) bool
	dfs = func(i int) bool {
		x1, y1, r1 := circles[i][0], circles[i][1], circles[i][2]
		if circleIntersectsBottomRightOfRectangle(x1, y1, r1, xCorner, yCorner) {
			return true
		}
		visited[i] = true
		for j := 0; j < len(circles); j++ {
			if !visited[j] && circlesIntersectInRectangle(x1, y1, r1, circles[j][0], circles[j][1], circles[j][2], xCorner, yCorner) && dfs(j) {
				return true
			}
		}
		return false
	}

	for i := range circles {
		x, y, r := circles[i][0], circles[i][1], circles[i][2]
		if pointInCircle(0, 0, x, y, r) || pointInCircle(xCorner, yCorner, x, y, r) {
			return false
		}
		if !visited[i] && circleIntersectsTopLeftOfRectangle(x, y, r, xCorner, yCorner) && dfs(i) {
			return false
		}
	}
	return true
}

func pointInCircle(px, py, x, y, r int) bool {
	return (x-px)*(x-px)+(y-py)*(y-py) <= r*r
}

func circleIntersectsTopLeftOfRectangle(x, y, r, xCorner, yCorner int) bool {
	return (abs(x) <= r && 0 <= y && y <= yCorner) ||
		(0 <= x && x <= xCorner && abs(y-yCorner) <= r) ||
		pointInCircle(x, y, 0, yCorner, r)
}

func circleIntersectsBottomRightOfRectangle(x, y, r, xCorner, yCorner int) bool {
	return (abs(y) <= r && 0 <= x && x <= xCorner) ||
		(0 <= y && y <= yCorner && abs(x-xCorner) <= r) ||
		pointInCircle(x, y, xCorner, 0, r)
}

func circlesIntersectInRectangle(x1, y1, r1, x2, y2, r2, xCorner, yCorner int) bool {
	return (x1-x2)*(x1-x2)+(y1-y2)*(y1-y2) <= (r1+r2)*(r1+r2) &&
		x1*r2+x2*r1 < (r1+r2)*xCorner &&
		y1*r2+y2*r1 < (r1+r2)*yCorner
}

func abs(x int) int {
	if x < 0 {
		return -x
	}
	return x
}

func main() {
	X := 3
	Y := 4
	circles := [][]int{{2, 1, 1}}
	result := canReachCorner(X, Y, circles)
	fmt.Println(result)
}

Python完整代码如下：

# -*-coding:utf-8-*-

def can_reach_corner(x_corner, y_corner, circles):
    visited = [False] * len(circles)

    def dfs(i):
        x1, y1, r1 = circles[i][0], circles[i][1], circles[i][2]
        if circle_intersects_bottom_right_of_rectangle(x1, y1, r1, x_corner, y_corner):
            return True
        visited[i] = True
        for j in range(len(circles)):
            if not visited[j] and circles_intersect_in_rectangle(x1, y1, r1, circles[j][0], circles[j][1], circles[j][2], x_corner, y_corner) and dfs(j):
                return True
        return False

    for i in range(len(circles)):
        x, y, r = circles[i][0], circles[i][1], circles[i][2]
        if point_in_circle(0, 0, x, y, r) or point_in_circle(x_corner, y_corner, x, y, r):
            return False
        if not visited[i] and circle_intersects_top_left_of_rectangle(x, y, r, x_corner, y_corner) and dfs(i):
            return False
    return True

def point_in_circle(px, py, x, y, r):
    return (x-px)*(x-px) + (y-py)*(y-py) <= r*r

def circle_intersects_top_left_of_rectangle(x, y, r, x_corner, y_corner):
    return (abs(x) <= r and 0 <= y <= y_corner) or \
           (0 <= x <= x_corner and abs(y-y_corner) <= r) or \
           point_in_circle(x, y, 0, y_corner, r)

def circle_intersects_bottom_right_of_rectangle(x, y, r, x_corner, y_corner):
    return (abs(y) <= r and 0 <= x <= x_corner) or \
           (0 <= y <= y_corner and abs(x-x_corner) <= r) or \
           point_in_circle(x, y, x_corner, 0, r)

def circles_intersect_in_rectangle(x1, y1, r1, x2, y2, r2, x_corner, y_corner):
    return (x1-x2)*(x1-x2) + (y1-y2)*(y1-y2) <= (r1+r2)*(r1+r2) and \
           x1*r2 + x2*r1 < (r1+r2)*x_corner and \
           y1*r2 + y2*r1 < (r1+r2)*y_corner

def abs_val(x):
    return -x if x < 0 else x

def main():
    x = 3
    y = 4
    circles = [[2, 1, 1]]
    result = can_reach_corner(x, y, circles)
    print(result)

if __name__ == "__main__":
    main()