2025-03-12：使数组等于目标数组所需的最少操作次数。用go语言，给定一个正整数数组 nums，Alice 和 Bob 正在进行一场游戏。游戏规则是，Alice 可以选择数组中所有的个位数或者所有的两位数，剩下的数字则由 Bob 得到。

如果 Alice 选择的数字总和大于 Bob 的数字总和，则她获胜。

请问，如果 Alice 有可能赢得这场游戏，返回 true；否则返回 false。

1 <= nums.length <= 100。

1 <= nums[i] <= 99。

输入：nums = [1,2,3,4,5,14]。

输出：true。

解释：

Alice 选择个位数可以赢得比赛，所选数字之和为 15。

答案2025-03-12：

题目来自leetcode3232。

大体步骤如下：

1.创建一个名为 canAliceWin 的函数，参数为一个整型数组 nums，返回一个布尔值来表示是否Alice可以赢得游戏。

2.在函数内部初始化两个变量 singleDigitSum 和 doubleDigitSum，分别用于记录个位数的总和和两位数的总和。

3.遍历数组 nums，对于每个元素执行以下操作：

- 如果当前数字小于10，则将其加入 `singleDigitSum` 中。

- 如果当前数字大于等于10，则将其加入 `doubleDigitSum` 中。

4.判断 singleDigitSum 是否等于 doubleDigitSum，如果不相等则返回 true，表示Alice可以赢得游戏；否则返回 false，表示Alice无法赢得游戏。

5.在 main 函数中定义一个数组 nums = [1,2,3,4,5,14] 作为示例输入。

6.调用 canAliceWin(nums) 函数得到返回值，将结果存储在 result 变量中。

7.最后打印输出 result，即Alice是否能赢得游戏。

总的时间复杂度为 O(n)，其中 n 为数组 nums 的长度。

总的额外空间复杂度为 O(1)，因为只使用了常量级别的额外空间。

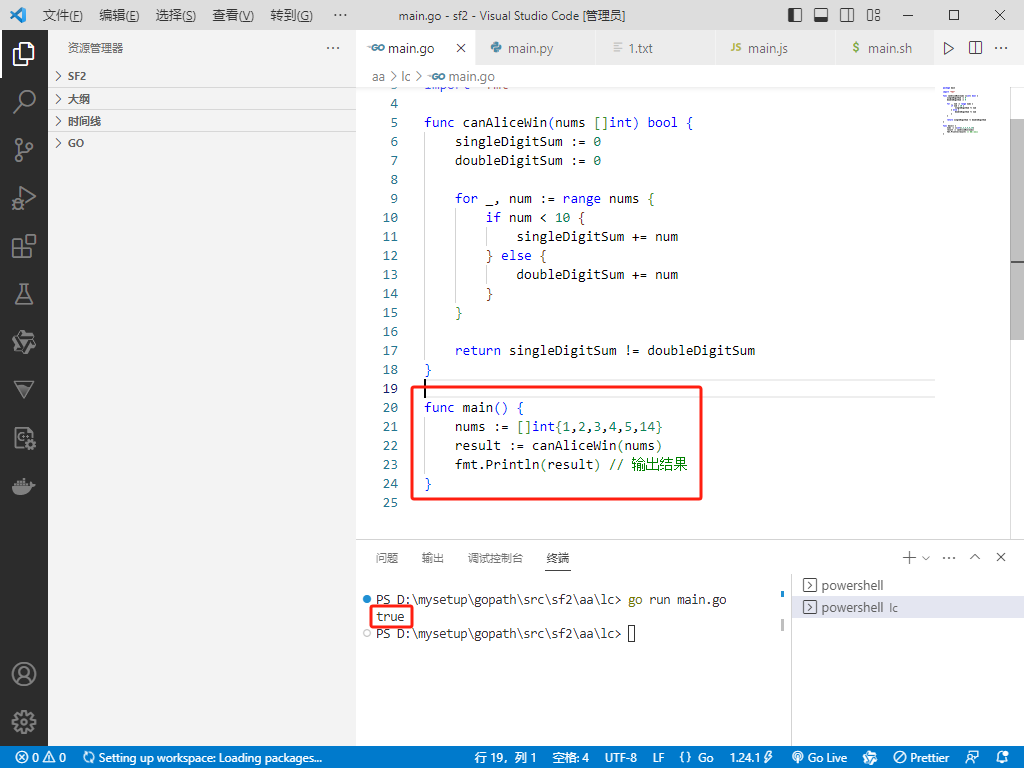
Go完整代码如下：

package main

import "fmt"

func canAliceWin(nums []int) bool {
    singleDigitSum := 0
    doubleDigitSum := 0

    for _, num := range nums {
        if num < 10 {
            singleDigitSum += num
        } else {
            doubleDigitSum += num
        }
    }

    return singleDigitSum != doubleDigitSum
}

func main() {
	nums := []int{1,2,3,4,5,14}
	result := canAliceWin(nums)
	fmt.Println(result) // 输出结果
}

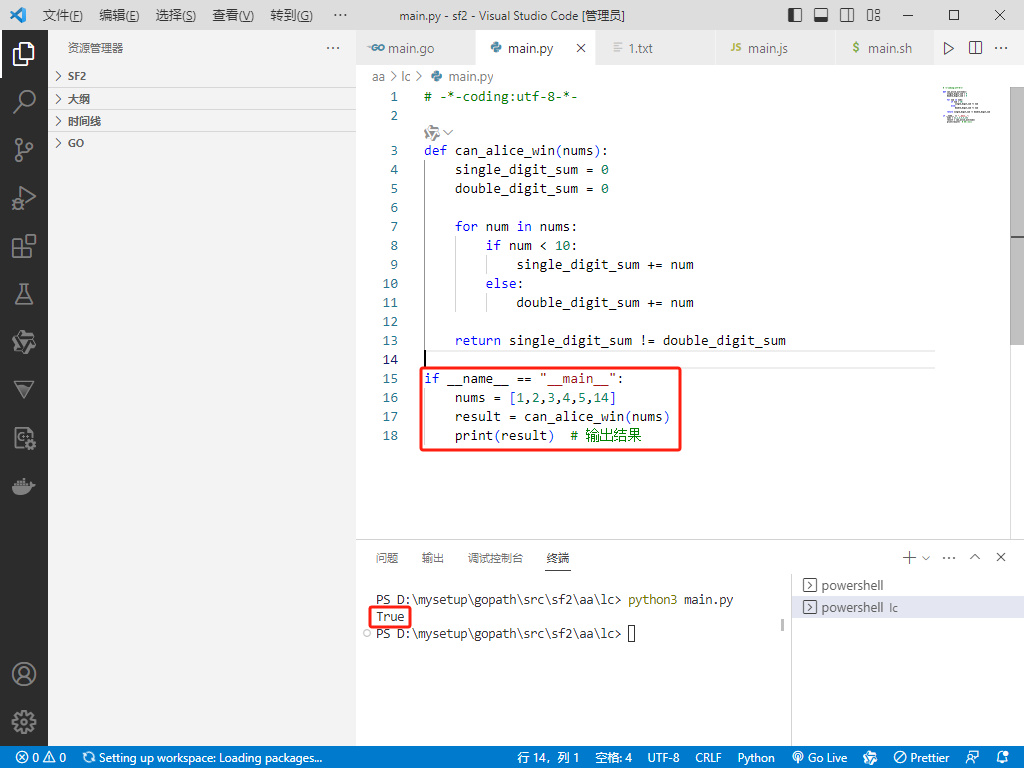
Python完整代码如下：

# -*-coding:utf-8-*-

def can_alice_win(nums):
    single_digit_sum = 0
    double_digit_sum = 0

    for num in nums:
        if num < 10:
            single_digit_sum += num
        else:
            double_digit_sum += num

    return single_digit_sum != double_digit_sum

if __name__ == "__main__":
    nums = [1,2,3,4,5,14]
    result = can_alice_win(nums)
    print(result)  # 输出结果