【数据结构与算法】快速排序（上）三种版本的实现

目录

一、引言

历史背景

地位

二、快速排序的基本原理和实现

🍃hoare版本

🍃挖坑法

🍃前后指针法

​

 一、引言

快速排序（Quick Sort）作为一种经典的排序算法，其历史背景和地位在计算机科学领域具有重要意义。

历史背景

1. 起源与提出

• 时间：快速排序算法由C. A. R. Hoare（通常被称为Tony Hoare）在1960年提出，但也有说法认为是在1962年。这一算法最初在Hoare的论文“Quicksort”中进行了详细描述，该论文于1961年发表在《Computer Journal》上。
• 背景：快速排序是对冒泡排序等简单排序算法的一种重大改进。冒泡排序虽然易于理解和实现，但其时间复杂度较高，达到了O(n^2)，这在处理大规模数据集时显得力不从心。因此，为了克服这一缺点，Hoare提出了快速排序算法。

2. 发展与优化

• 优化策略：自快速排序提出以来，许多研究者对其进行了深入的研究和优化。这些优化策略包括但不限于：基准值的选择（如随机选择、三数中值分割等）、尾递归优化、小数组优化（当子数组较小时改用插入排序等更高效的算法）、并行快速排序等。
• 广泛应用：随着计算机科学的不断发展，快速排序算法得到了广泛的应用。它不仅在数据排序中发挥着重要作用，还被应用于数据库管理、文件排序、数据分析等多个领域。

地位

1. 经典算法之一

• 快速排序是计算机科学中最著名的排序算法之一，与归并排序、堆排序等算法齐名。它以其简洁的算法逻辑和高效的性能表现，成为了排序算法中的佼佼者。

2. 广泛使用

• 快速排序在实际应用中具有广泛的适用性。无论是编程语言的标准库（如Python的sorted函数、Java的Arrays.sort方法等）还是各种数据处理系统（如数据库管理系统、数据分析工具等），都广泛采用了快速排序算法或其变种。

3. 面试与竞赛常见

• 由于快速排序算法的重要性，它经常出现在各种编程面试和算法竞赛中。掌握快速排序算法的原理和实现方式，对于提高编程能力和应对面试、竞赛等挑战具有重要意义。

二、快速排序的基本原理和实现

🍃hoare版本

基本原理

​编辑

实现思路：

1. 递归终止条件：首先检查left（左边界）是否大于等于right（右边界），如果是，则说明当前子数组的长度小于或等于1，此时不需要排序，直接返回。

2. 选择基准值：这里选择子数组的第一个元素a[left]作为基准值（keyi），并将keyi的索引保存在keyi变量中。

3. 分区操作：

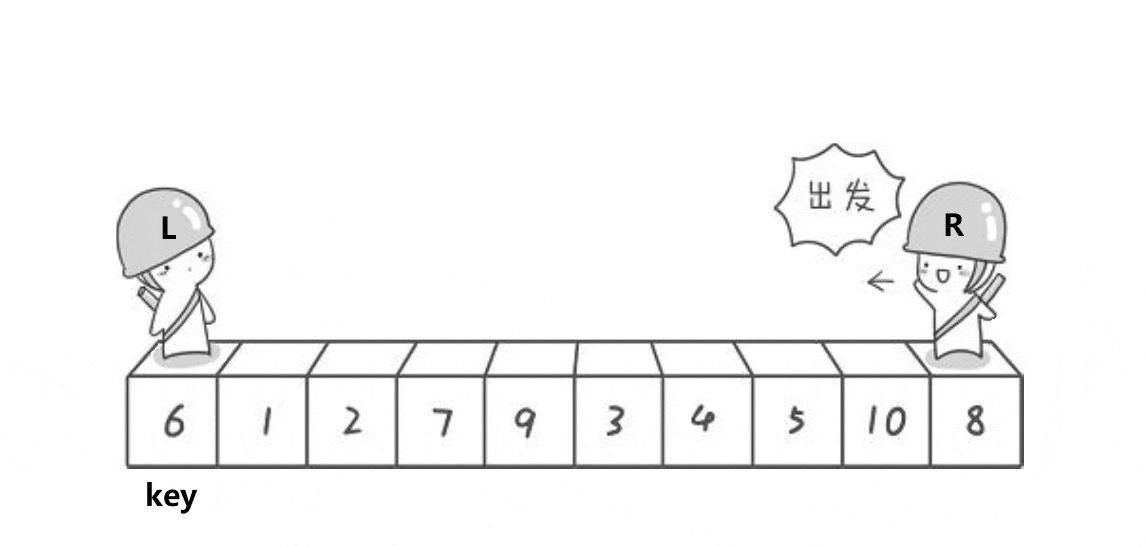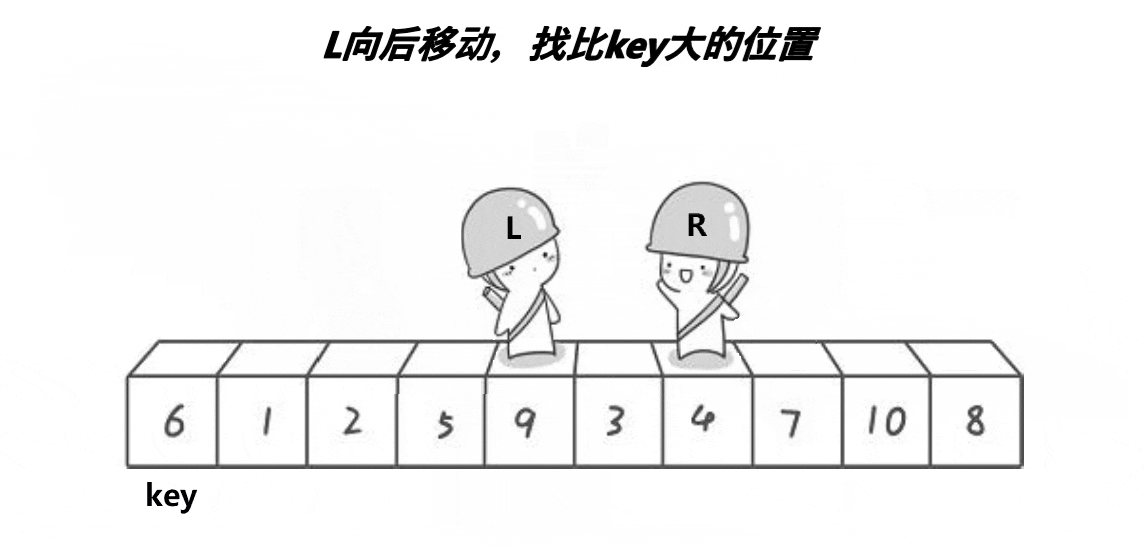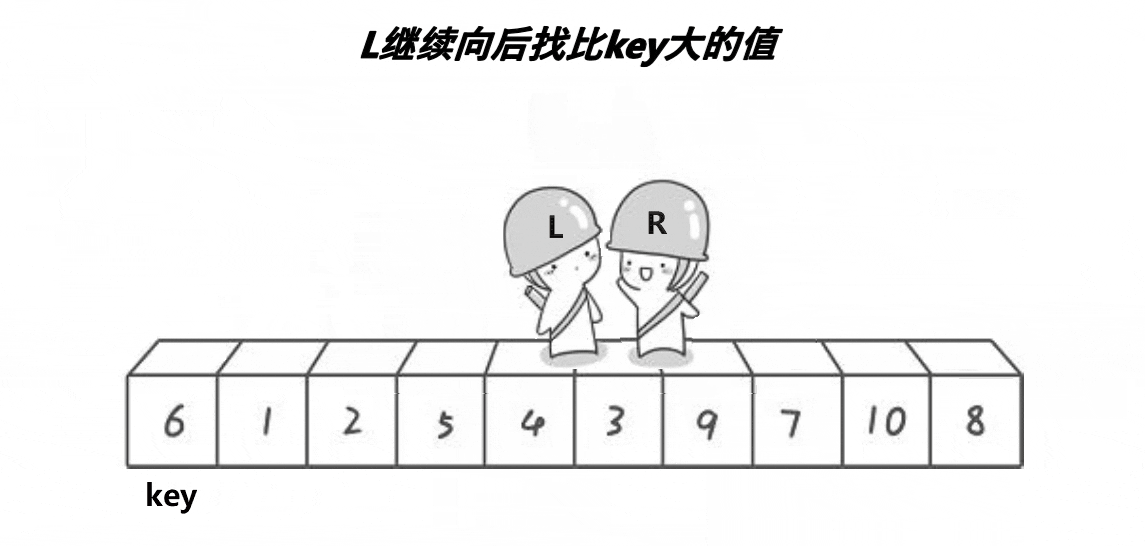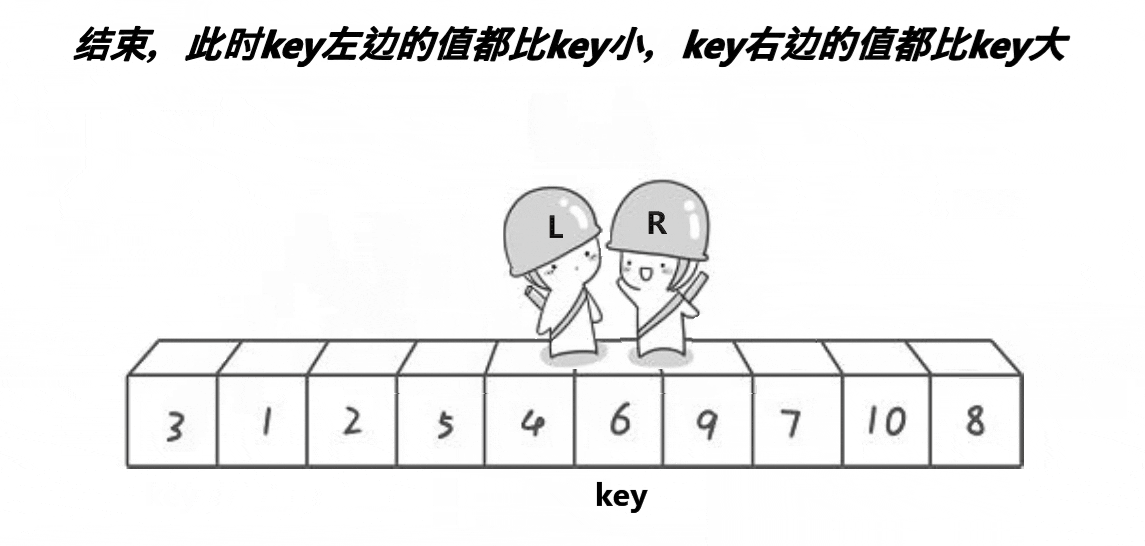
   • 使用两个指针begin和end，分别从数组的左右两端开始扫描。
   • end指针从右向左移动，直到找到一个小于或等于基准值的元素。
   • 同时，begin指针从左向右移动，直到找到一个大于基准值的元素。
   • 如果begin和end没有相遇（即begin < end），则交换a[begin]和a[end]的值，然后继续移动指针。
   • 这个过程会一直进行，直到begin和end相遇或交错。
   • 当begin和end相遇时，将基准值（即a[keyi]）与a[begin]（此时begin == end）交换，这样基准值就被放到了它最终应该在的位置。

4. 递归排序：

   • 更新keyi的值为begin（即基准值最终所在的位置）。
   • 然后，对基准值左边的子数组（left到keyi-1）和右边的子数组（keyi+1到right）分别递归调用Quicksort1函数进行排序。

优势与特点：

• Hoare版本的快速排序在分区时，begin和end指针是同时从数组的两端向中间移动，这有助于减少数据移动的次数，尤其是在数组已经部分有序的情况下。
• 该算法的时间复杂度平均为O(n log n)，但在最坏情况下（如数组已经有序或逆序）会退化到O(n^2)。为了改善最坏情况的表现，可以参考本文后面的优化策略。

注意：在实际应用中，快速排序的性能很大程度上取决于基准值的选择和分区策略。Hoare版本的分区策略相对简单，但在某些情况下可能不是最优的。

C语言实现代码

void Swap(int* a, int* b)//交换函数
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}
// 快速排序hoare版本
void  Quicksort1(int* a, int left, int right)
{
	if (left >= right)//只有一个元素或不存在，停止递归
		return ;

	int keyi = left;
	int begin = left, end = right;

	while (begin < end)//begin与end未相遇时，继续循环
	{
		while (begin < end && a[end] >= a[keyi])//end先移动，找到小于keyi位置的值停止
			end--;
		while (begin < end && a[begin] <= a[keyi])//begin再移动，找到大于keyi位置的值停止
			begin++;
		Swap(&a[begin], &a[end]);
	}
	Swap(&a[keyi], &a[begin]);//出循环后，begin与end相遇，交换此位置与keyi位置的值

	keyi = begin;//更新keyi的位置
	//[left][keyi-1]keyi[keyi+1][right]  左右区间划分
	Quicksort1(a, left, keyi - 1);//左区间递归
	Quicksort1(a, keyi + 1, right);//右区间递归
}

🍃挖坑法

基本原理

​编辑

实现思路：

1. 终止条件：首先检查left（左边界）是否大于等于right（右边界），如果是，则当前子数组的长度小于或等于1，不需要排序，直接返回。

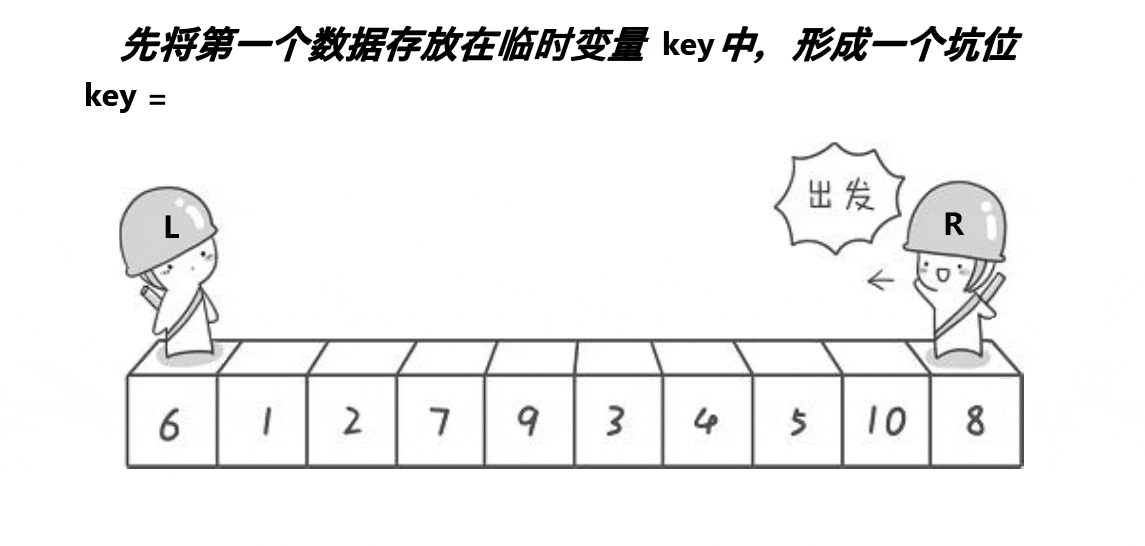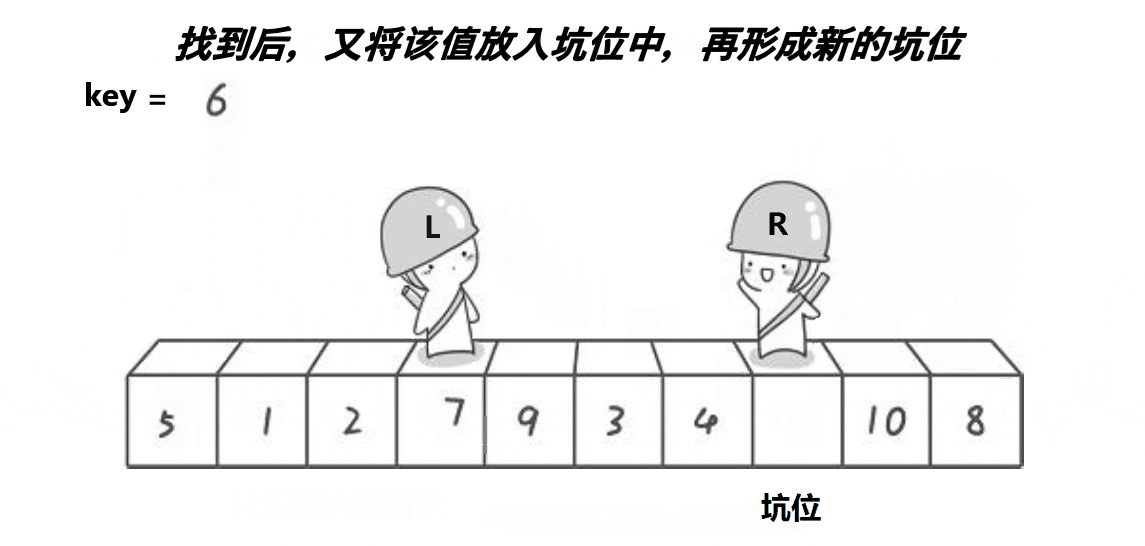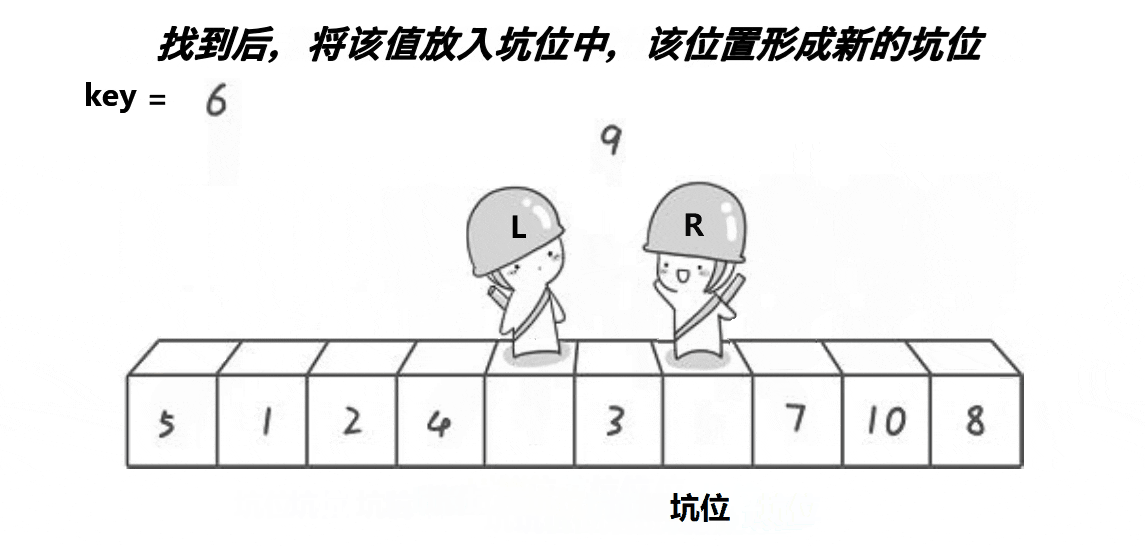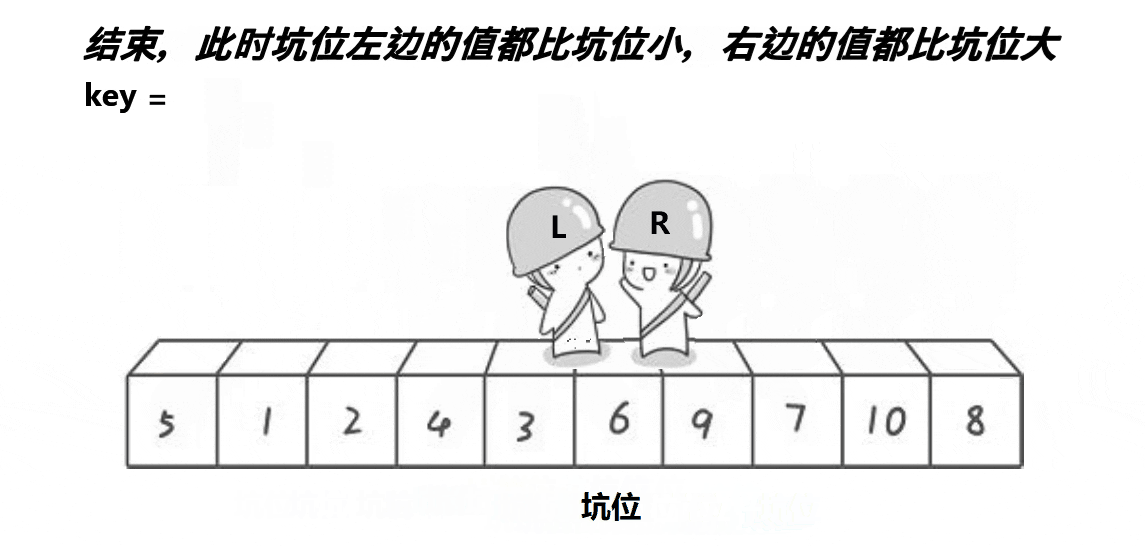
2. 选择基准值：选择子数组的第一个元素a[left]作为基准值，并将其存储在临时变量tmp中。这里的tmp用于后续将基准值放回到其在排序后数组中的正确位置。

3. 分区操作（挖坑法）：

   • 使用两个指针begin和end，分别初始化为left和right。这两个指针用于从数组的两端开始向中间扫描。
   • end指针从右向左移动，寻找第一个小于基准值tmp的元素。找到后，将该元素的值放到begin指针所指的“坑”中（如果begin和end没有相遇）。
   • 然后，begin指针从左向右移动，寻找第一个大于基准值tmp的元素。找到后，将该元素的值放到end指针所指的“坑”中（注意，此时end已经向左移动过，所以不会覆盖之前放置的值）。
   • 这个过程会一直进行，直到begin和end相遇或交错。此时，begin（或end，因为它们相遇了）所在的位置就是基准值tmp应该放置的位置。

4. 放置基准值：将保存在tmp中的基准值放到begin（或end，它们现在相同）所指的位置。这个位置就是基准值在排序后数组中的正确位置。

5. 递归排序：

   • 现在，基准值已经处于其最终位置，我们可以将数组分为左右两个子数组进行递归排序。
   • 左子数组的范围是从left到keyi - 1（因为keyi现在是基准值的正确位置）。
   • 右子数组的范围是从keyi + 1到right。

优势与特点：

• 挖坑法的特点是它始终将基准值（在这个例子中是tmp）保留在外部变量中，直到分区操作完成后再将其放回到数组中。这种方法简化了分区过程中元素的交换逻辑，但可能需要额外的空间来存储基准值。不过，在这个特定的实现中，基准值是从数组中直接取出的，所以并没有额外的空间开销。

C语言实现代码

void Quicksort2(int* a, int left, int right)
{
	if (left >= right)//只有一个元素或不存在，停止递归
		return;
	int tmp = a[left];//先将基准值存下来
	int keyi = left;
	int begin = left, end = right;
	while (begin < end)
	{
		while (begin < end && a[end] <= tmp)//右找大，找到停下来，填到左边的坑
			end--;
		if(begin<end)
			a[begin] = a[end];
		
		while (begin < end && a[begin] >= tmp)//左找小，找到停下来，填到右边的坑
			begin++;
		if(begin<end)
			a[end] = a[begin];
	}
	a[begin] = tmp;//相遇之后，将保存的值填到相遇位置

	keyi = begin;
	Quicksort2(a, left, keyi - 1);
	Quicksort2(a, keyi + 1, right);

}

🍃前后指针法

基本原理

​编辑

实现思路：

1. 终止条件：首先检查left（左边界）是否大于等于right（右边界），如果是，则当前子数组的长度小于或等于1，不需要排序，直接返回。

2. 选择基准值：选择子数组的第一个元素a[left]作为基准值，并将该位置的索引存储在keyi变量中。虽然这个索引在后续操作中没有被直接用于交换，但它用于在分区结束后确定基准值的最终位置。

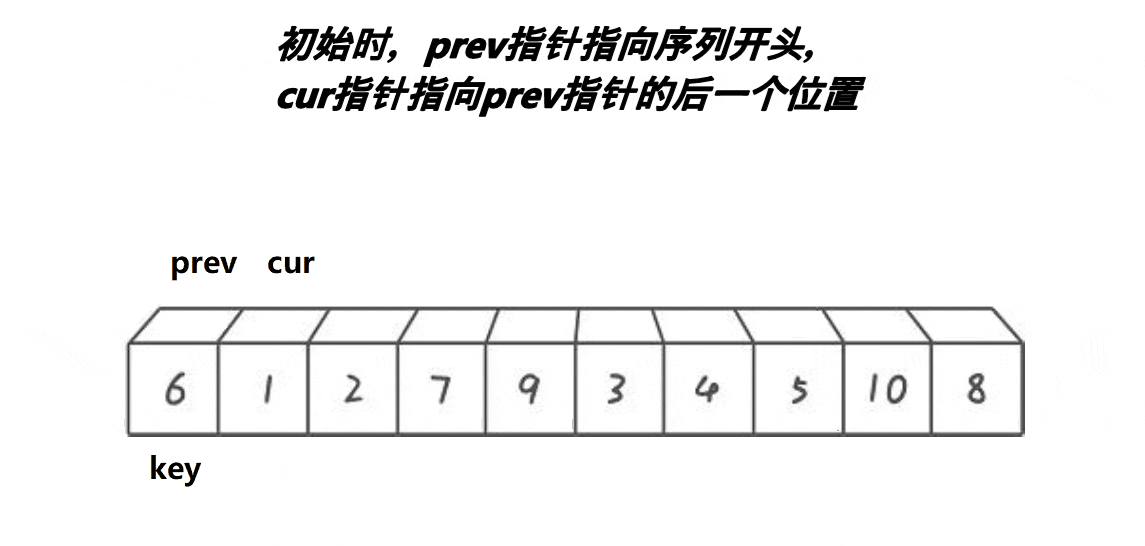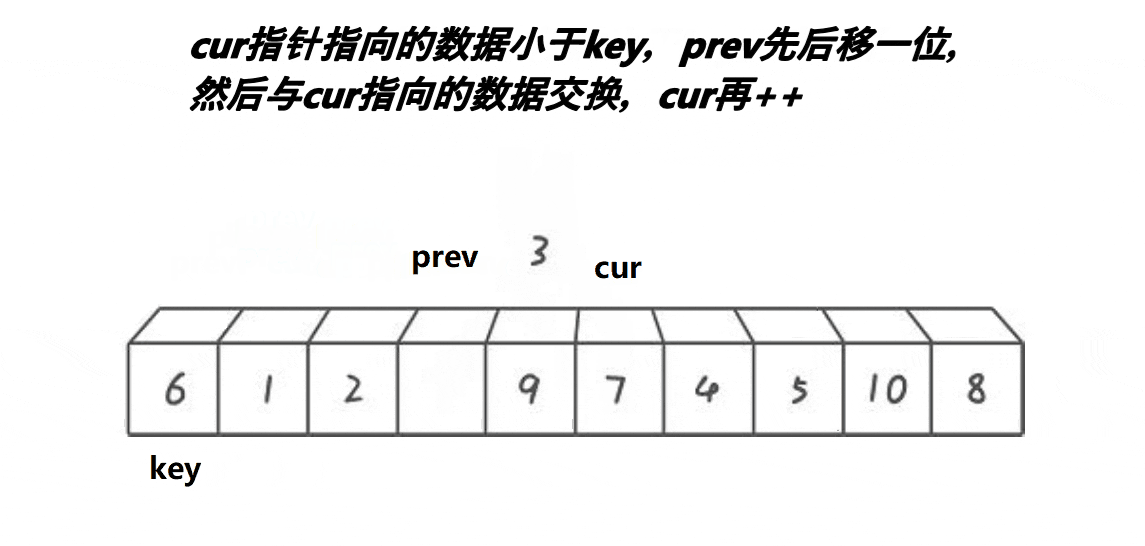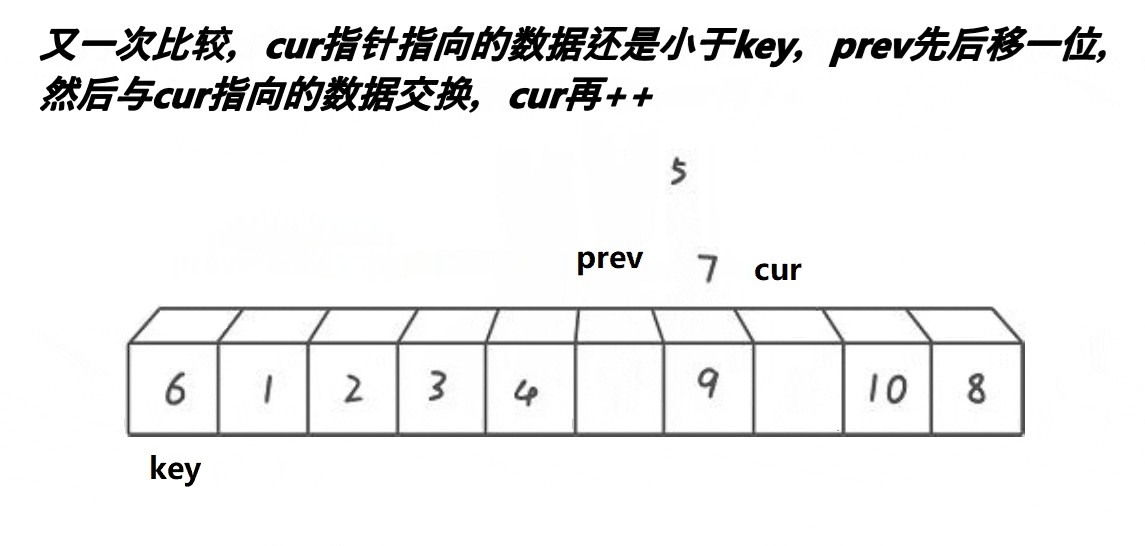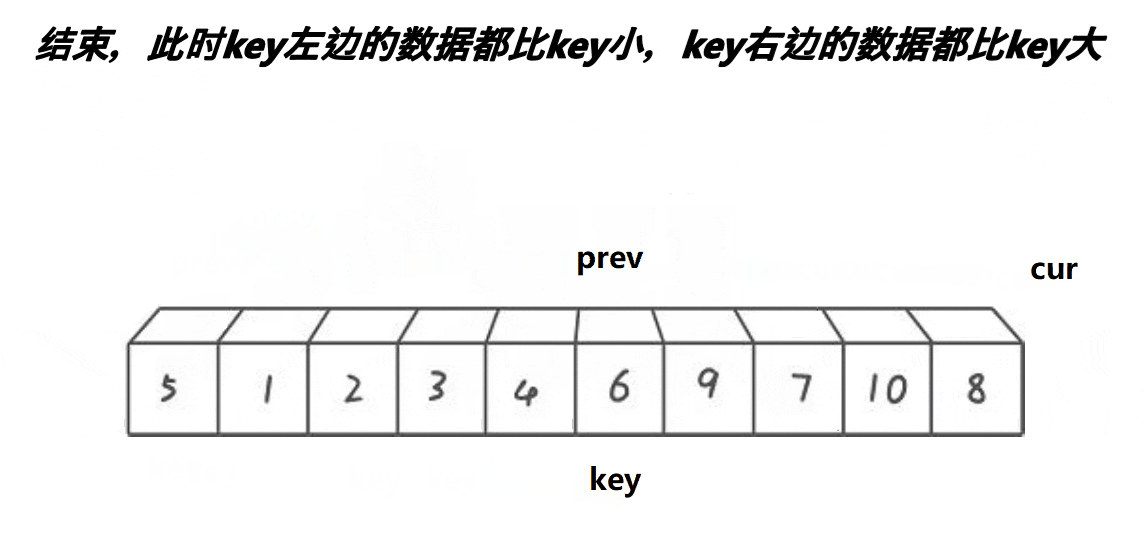
3. 初始化指针：

   • prev（前指针）初始化为left，它用于记录小于基准值的最后一个元素的位置。
   • cur（后指针）初始化为left + 1，它用于遍历数组中的元素，寻找小于基准值的元素。

4. 分区操作：

   • 使用while循环，当cur小于等于right时执行循环体。
   • 在循环体内，如果a[cur]小于基准值a[keyi]，并且prev没有指向当前cur的位置（即prev++ != cur，这是为了避免自身与自身的无用交换），则将a[prev]和a[cur]的值交换。然后，prev向前移动一步（prev++在条件判断之后执行，确保只有在需要时才进行交换和移动）。
   • cur始终向前移动，直到遍历完整个子数组。

5. 放置基准值：

   • 当cur遍历完整个子数组后，循环结束。此时，prev指向的是最后一个小于基准值的元素的位置（注意，如果所有元素都大于等于基准值，则prev将停留在left位置）。
   • 将基准值a[keyi]与a[prev]交换，这样基准值就被放到了它最终应该在的位置。

6. 更新基准值位置：

   • 由于基准值已经与a[prev]交换，所以将keyi更新为prev，以反映基准值的新位置。

7. 递归排序：

   • 对基准值左边的子数组（left到keyi - 1）和右边的子数组（keyi + 1到right）分别递归调用Quicksort3函数进行排序。

优势与特点：

• 代码实现相对简洁，与其他版本相比，代码更不容易出错，边界控制也更为容易
• 与hoare版本相同，一般情况下会多出一些数据交换（因为较大的数据不是直接移动到该在的位置），但最终效率影响不大

C语言实现代码

void Swap(int* a, int* b)//交换函数
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}
void Quicksort3(int* a, int left, int right)
{
	if (left >= right)//只有一个元素或不存在，停止递归
		return;
	int keyi = left;

	int prev = left;//前指针
	int cur = left + 1;//后指针
	while (cur <= right)//cur越界结束循环
	{
		//cur一直向后走，遇到小的值就停下，让prev向前走一步并交换
		if (a[cur] < a[keyi] && prev++ != cur)//prev++ != cur是为了避免无用的原地交换
			Swap(&a[prev], &a[cur]);
		cur++;
	}
	Swap(&a[keyi], &a[prev]);//出循环，将prev停留位置与keyi位置进行交换

	keyi = prev;
	Quicksort3(a, left, keyi - 1);
	Quicksort3(a, keyi + 1, right);
}

​