2024-11-26：使数组中位数等于 K 的最少操作数。用go语言，给定一个整数数组 nums 和一个非负整数 k，

你可以通过选择数组中的任意元素进行加 1 或减 1 的操作。

请计算将 nums 的中位数调整为 k 所需的最小操作次数。

中位数是指将数组排序后位于中间位置的元素。

如果数组的长度为偶数，则中位数为中间两个元素中较大的那个。

输入：nums = [2,5,6,8,5], k = 4。

输出：2。

解释：我们将 nums[1] 和 nums[4] 减 1 得到 [2, 4, 6, 8, 4] 。现在数组的中位数等于 k 。

答案2024-11-26：

chatgpt

题目来自leetcode3107。

大体步骤如下：

1.输入数据：

• 有一个整数数组 nums，在本例中为 [2, 5, 6, 8, 5]。

• 一个非负整数 k，在这里为 4。

2.排序数组：

• 首先，需要对 nums 数组进行排序。经过排序后，nums 变为 [2, 5, 5, 6, 8]。

3.确定中位数的索引：

• 计算数组的中位数索引 m。对于长度为 5（奇数）的数组，中位数位于索引 m = len(nums) / 2 = 5 / 2 = 2。中位数值为 nums[m] = 5。

4.比较中位数与 k：

• 接下来，检查中位数 5 是否大于、等于或小于 k。

• 在本例中，5 大于 k（4），因此我们将进行减少操作。

5.减少中位数到 k：

5.1.从中位数索引开始向左迭代数组（从索引 m 到 0），如果遇到的元素大于 k，则执行减 1 操作。

5.2.在本例中，进行以下操作：

5.2.1.从索引 2 开始，nums[2] = 5。执行 5 - 4 = 1 操作，累计操作次数 ans += 1，ans 变为 1。

5.2.2.向左移动到索引 1，nums[1] = 5。再次执行 5 - 4 = 1 操作，累计操作次数再次增加 1，ans 变为 2。

5.2.3.向左移动到索引 0，nums[0] = 2。因为 2 小于 k，停止左侧迭代。

6.完成操作：

• 在整个过程中，我们共进行了 2 次操作，两次将大于 k 的值减少到 k，最终将中位数调整为 4。

7.输出结果：

• 最后，函数返回的最小操作次数 2 作为结果，表示需要通过两次操作才能使 nums 的中位数等于 k。

时间复杂度和空间复杂度

• 时间复杂度：

  • 对数组进行排序的时间复杂度为 O(n log n)，其中 n 是数组的长度。

  • 之后遍历数组以计算操作次数的复杂度为 O(n)。因此，总的时间复杂度为 O(n log n)。

• 空间复杂度：

  • 排序通常是 O(1) 的额外空间复杂度，因为排序是就地进行的，尽管具体实现可能会有所不同。在本解决方案中，使用的额外空间主要是临时变量，故总体额外空间复杂度为 O(1)。

总结起来，这段代码的复杂度分析是：

• 总时间复杂度：O(n log n)

• 总空间复杂度：O(1)

Go完整代码如下：

package main

import (
	"fmt"
	"slices"
)

func minOperationsToMakeMedianK(nums []int, k int) (ans int64) {
	slices.Sort(nums)
	m := len(nums) / 2
	if nums[m] > k {
		for i := m; i >= 0 && nums[i] > k; i-- {
			ans += int64(nums[i] - k)
		}
	} else {
		for i := m; i < len(nums) && nums[i] < k; i++ {
			ans += int64(k - nums[i])
		}
	}
	return
}

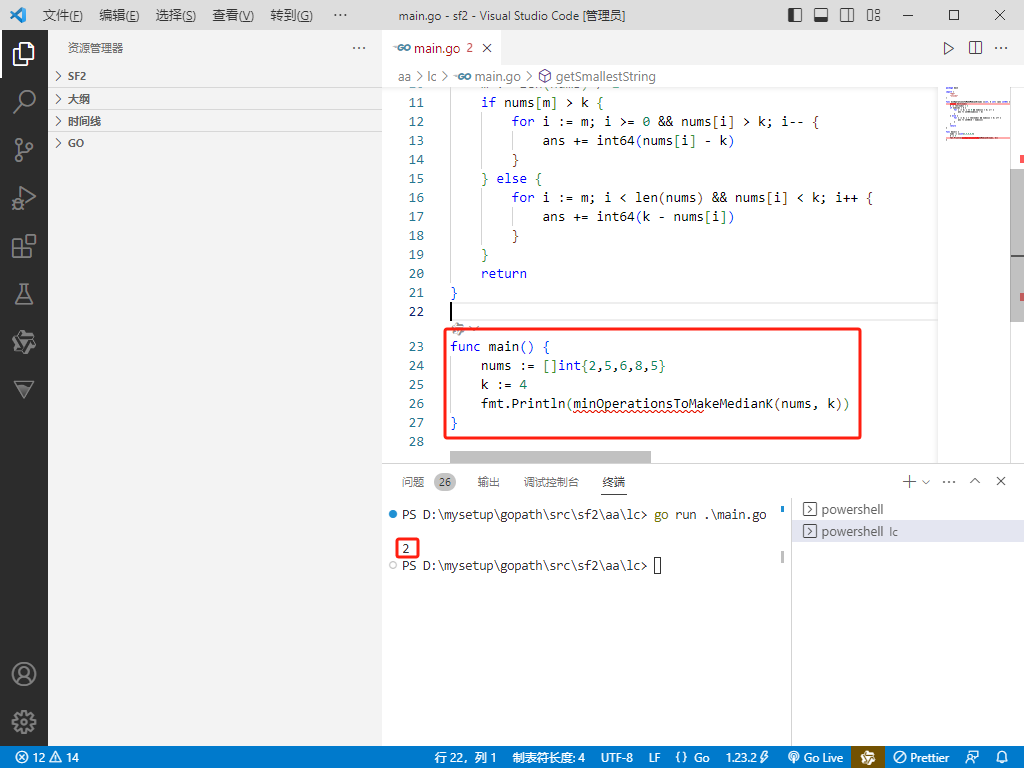
func main() {
	nums := []int{2,5,6,8,5}
	k := 4
	fmt.Println(minOperationsToMakeMedianK(nums, k))
}

Rust完整代码如下：

use std::cmp::Ordering;

fn min_operations_to_make_median_k(nums: &mut Vec<i32>, k: i32) -> i64 {
    // 首先对数组进行排序
    nums.sort();
    let m = nums.len() / 2;
    let mut ans = 0;

    // 判断中位数与 k 的关系
    if nums[m] > k {
        for i in (0..=m).rev() { // 从中位数向左遍历
            if nums[i] > k {
                ans += (nums[i] - k) as i64; // 计算减少的操作数
            }
        }
    } else {
        for i in m..nums.len() { // 从中位数向右遍历
            if nums[i] < k {
                ans += (k - nums[i]) as i64; // 计算增加的操作数
            }
        }
    }
    ans
}

fn main() {
    let mut nums = vec![2, 5, 6, 8, 5];
    let k = 4;
    println!("{}", min_operations_to_make_median_k(&mut nums, k));
}