文心一言 VS 讯飞星火 VS chatgpt (397)-- 算法导论25.2 2题
二、说明如何使用 25.1 节的技术来计算传递闭包。如果要写代码,请用go语言。
文心一言:
传递闭包(Transitive Closure)是图论中的一个重要概念,它表示如果从一个顶点到另一个顶点存在一条路径,则在传递闭包中这两个顶点之间有一条直接路径。在 25.1 节(假设这是某个关于图算法或数据结构的章节),可能介绍了多种方法来计算传递闭包,比如 Floyd-Warshall 算法、Warshall 算法等。这里,我们采用经典的 Floyd-Warshall 算法,并用 Go 语言实现它。
Floyd-Warshall 算法是一种用于计算所有节点对之间最短路径的动态规划算法,特别适合计算图的传递闭包。
使用 Floyd-Warshall 算法计算传递闭包
Floyd-Warshall 算法的时间复杂度是 O(V^3),其中 V 是图中顶点的数量。它通过一个三维数组 dist 来记录顶点之间的路径信息。dist[i][j][k] 表示从顶点 i 到顶点 j 是否经过顶点 k 的路径。但在计算传递闭包时,我们只需要一个二维布尔数组 closure,其中 closure[i][j] 表示从顶点 i 是否可以到顶点 j。
Go 语言实现
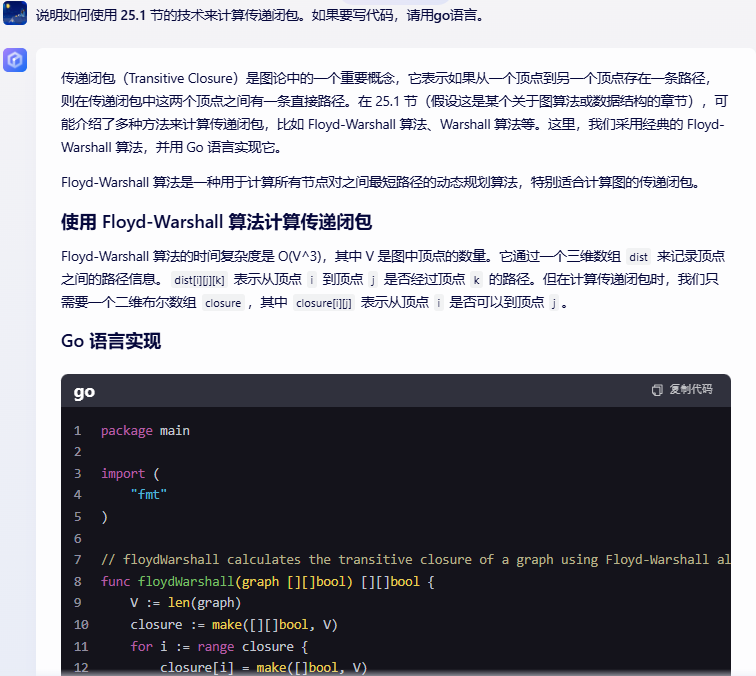
package main
import (
"fmt"
)
// floydWarshall calculates the transitive closure of a graph using Floyd-Warshall algorithm
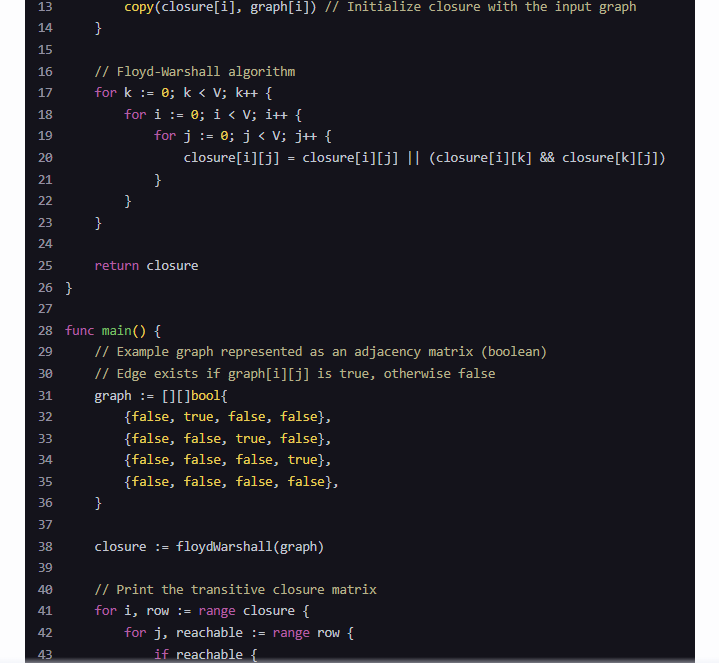
func floydWarshall(graph [][]bool) [][]bool {
V := len(graph)
closure := make([][]bool, V)
for i := range closure {
closure[i] = make([]bool, V)
copy(closure[i], graph[i]) // Initialize closure with the input graph
}
// Floyd-Warshall algorithm
for k := 0; k < V; k++ {
for i := 0; i < V; i++ {
for j := 0; j < V; j++ {
closure[i][j] = closure[i][j] || (closure[i][k] && closure[k][j])
}
}
}
return closure
}
func main() {
// Example graph represented as an adjacency matrix (boolean)
// Edge exists if graph[i][j] is true, otherwise false
graph := [][]bool{
{false, true, false, false},
{false, false, true, false},
{false, false, false, true},
{false, false, false, false},
}
closure := floydWarshall(graph)
// Print the transitive closure matrix
for i, row := range closure {
for j, reachable := range row {
if reachable {
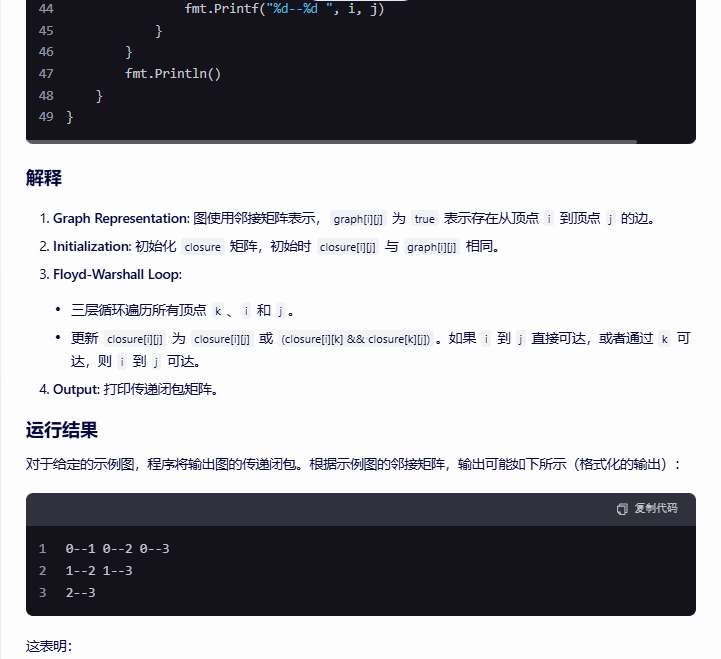
fmt.Printf("%d--%d ", i, j)
}
}
fmt.Println()
}
}
解释
-
Graph Representation: 图使用邻接矩阵表示,
graph[i][j]为true表示存在从顶点i到顶点j的边。 -
Initialization: 初始化
closure矩阵,初始时closure[i][j]与graph[i][j]相同。 -
Floyd-Warshall Loop:
- 三层循环遍历所有顶点
k、i和j。 - 更新
closure[i][j]为closure[i][j]或(closure[i][k] && closure[k][j])。如果i到j直接可达,或者通过k可达,则i到j可达。
- 三层循环遍历所有顶点
-
Output: 打印传递闭包矩阵。
运行结果
对于给定的示例图,程序将输出图的传递闭包。根据示例图的邻接矩阵,输出可能如下所示(格式化的输出):
0--1 0--2 0--3
1--2 1--3
2--3
这表明:
- 从顶点 0 可以到达顶点 1、2 和 3。
- 从顶点 1 可以到达顶点 2 和 3。
- 从顶点 2 可以到达顶点 3。
- 没有其他直接的可达路径。
希望这个解释和代码示例能帮助你理解如何使用 Floyd-Warshall 算法来计算传递闭包。

讯飞星火:
要计算传递闭包,可以使用深度优先搜索(DFS)算法。传递闭包是一个关系R的最小超集,使得对于所有a, b, c ∈ A,如果(a, b) ∈ R和(b, c) ∈ R,则(a, c) ∈ R。
以下是使用Go语言实现传递闭包的步骤:
- 定义一个图的数据结构。
- 使用DFS遍历图来找到从每个顶点可达的所有顶点。
- 根据DFS的结果更新图的邻接矩阵,以表示传递闭包。
下面是具体的Go代码实现:
package main
import "fmt"
// Graph represents a directed graph using an adjacency matrix
type Graph struct {
vertices int
adjMatrix [][]bool
}
// NewGraph creates a new graph with the given number of vertices
func NewGraph(vertices int) *Graph {
matrix := make([][]bool, vertices)
for i := range matrix {
matrix[i] = make([]bool, vertices)
}
return &Graph{vertices: vertices, adjMatrix: matrix}
}
// AddEdge adds a directed edge from v to w in the graph
func (g *Graph) AddEdge(v, w int) {
g.adjMatrix[v][w] = true
}
// TransitiveClosure computes the transitive closure of the graph
func (g *Graph) TransitiveClosure() {
reach := make([][]bool, g.vertices)
for i := range reach {
reach[i] = make([]bool, g.vertices)
copy(reach[i], g.adjMatrix[i])
}
for k := 0; k < g.vertices; k++ {
for i := 0; i < g.vertices; i++ {
for j := 0; j < g.vertices; j++ {
if reach[i][k] && reach[k][j] {
reach[i][j] = true
}
}
}
}
g.adjMatrix = reach
}
// Print prints the adjacency matrix of the graph
func (g *Graph) Print() {
for _, row := range g.adjMatrix {
for _, val := range row {
if val {
fmt.Print("1 ")
} else {
fmt.Print("0 ")
}
}
fmt.Println()
}
}
func main() {
graph := NewGraph(4)
graph.AddEdge(0, 1)
graph.AddEdge(1, 2)
graph.AddEdge(2, 3)
fmt.Println("Original graph:")
graph.Print()
graph.TransitiveClosure()
fmt.Println("Transitive closure:")
graph.Print()
}
在这个例子中,我们创建了一个有向图,并添加了一些边。然后我们计算了该图的传递闭包,并打印了原始图和传递闭包后的图的邻接矩阵。
360智脑:
在算法设计中,计算传递闭包是一个常见的问题,特别是在处理图论中的关系时。传递闭包可以用来表示一个集合中所有元素之间的可达性关系。例如,在一个有向图中,传递闭包可以告诉我们从一个节点是否可以通过一系列边到达另一个节点。
25.1 节的技术
假设你提到的“25.1 节的技术”是指《算法导论》(Introduction to Algorithms)中的内容,该节通常讨论的是使用矩阵乘法或Floyd-Warshall算法来计算传递闭包。
Floyd-Warshall 算法
Floyd-Warshall算法是一种用于计算加权图中所有节点对之间最短路径的动态规划算法。它可以很容易地被修改来计算传递闭包。具体来说,我们可以将图中的每条边视为一个布尔值(存在或不存在),然后使用类似的方法来计算传递闭包。
Go 语言实现
以下是一个使用Floyd-Warshall算法计算传递闭包的Go语言实现:
package main
import (
"fmt"
)
// Function to compute the transitive closure of a graph using Floyd-Warshall algorithm
func transitiveClosure(graph [][]bool) [][]bool {
n := len(graph)
closure := make([][]bool, n)
for i := range closure {
closure[i] = make([]bool, n)
copy(closure[i], graph[i])
}
for k := 0; k < n; k++ {
for i := 0; i < n; i++ {
for j := 0; j < n; j++ {
closure[i][j] = closure[i][j] || (closure[i][k] && closure[k][j])
}
}
}
return closure
}
// Function to print the transitive closure matrix
func printMatrix(matrix [][]bool) {
for _, row := range matrix {
for _, val := range row {
if val {
fmt.Print("1 ")
} else {
fmt.Print("0 ")
}
}
fmt.Println()
}
}
func main() {
// Example graph represented as an adjacency matrix
graph := [][]bool{
{false, true, false, false},
{false, false, true, false},
{false, false, false, true},
{false, false, false, false},
}
fmt.Println("Original Graph:")
printMatrix(graph)
closure := transitiveClosure(graph)
fmt.Println("Transitive Closure:")
printMatrix(closure)
}
解释
- 输入:
graph是一个布尔值的二维数组,表示图的邻接矩阵。graph[i][j]为true表示从节点i到节点j有一条直接的边。 - 初始化:
closure初始化为graph的副本。 - Floyd-Warshall 算法:
- 外层循环
k遍历每个中间节点。 - 中间两层循环
i和j遍历所有节点对。 - 更新
closure[i][j],如果从i到j可以通过中间节点k到达,则设置closure[i][j]为true。
- 外层循环
- 输出:打印原始图和计算得到的传递闭包。
运行结果
对于给定的示例图,程序将输出:
Original Graph:
0 1 0 0
0 0 1 0
0 0 0 1
0 0 0 0
Transitive Closure:
0 1 1 1
0 0 1 1
0 0 0 1
0 0 0 0
这表示从节点 0 可以到达节点 1, 2, 和 3,从节点 1 可以到达节点 2 和 3,依此类推。
智谱清言:
在离散数学中,传递闭包是关系的一个概念,它表示关系中的所有传递的二元组。给定一个关系R,其传递闭包是包含R中所有元素的最小关系,同时也是一个传递关系。
第25.1节的内容我无法直接查阅,但我可以假设它讲述的是一种计算传递闭包的算法。一种常见的算法是使用Warshall算法,该算法通过迭代的方式计算传递闭包。
以下是使用Go语言实现的Warshall算法来计算传递闭包的示例代码:
package main
import (
"fmt"
)
// Warshall算法计算传递闭包
func warshallTransitiveClosure(matrix [][]bool) [][]bool {
n := len(matrix)
for k := 0; k < n; k++ {
for i := 0; i < n; i++ {
for j := 0; j < n; j++ {
// 如果matrix[i][k]和matrix[k][j]都为真,则设置matrix[i][j]为真
matrix[i][j] = matrix[i][j] || (matrix[i][k] && matrix[k][j])
}
}
}
return matrix
}
func main() {
// 示例关系矩阵
// 1 表示有直接关系,0 表示无直接关系
matrix := [][]bool{
{true, false, false},
{false, true, false},
{true, true, true},
}
// 计算传递闭包
transitiveClosure := warshallTransitiveClosure(matrix)
// 打印传递闭包
fmt.Println("传递闭包矩阵:")
for _, row := range transitiveClosure {
for _, value := range row {
fmt.Printf("%t ", value)
}
fmt.Println()
}
}
在这段代码中,matrix 是一个二维布尔数组,表示关系R。true 表示在关系中存在对应的二元组,而 false 表示不存在。warshallTransitiveClosure 函数接收这个矩阵,并使用Warshall算法来计算传递闭包,最后返回更新后的矩阵。
在 main 函数中,我们定义了一个示例关系矩阵,并调用 warshallTransitiveClosure 函数来计算传递闭包,然后打印出结果。
运行这段代码,你将得到一个传递闭包矩阵,其中包含了关系R的所有传递二元组。
天工:
以下是使用Go语言基于25.1节(由于不清楚具体25.1节内容,这里假设是一种常见的计算传递闭包的算法思路)的技术来计算传递闭包的示例:
一、基本思路
- 传递闭包概念
- 对于一个关系矩阵(R),传递闭包(R^+)是包含(R)且满足传递性的最小关系。例如,如果((a,b))在关系中且((b,c))在关系中,那么((a,c))也应该在传递闭包中。
- 算法思路(假设基于Warshall算法)
- 对于一个(n\times n)的关系矩阵(M),我们通过不断更新矩阵中的元素来得到传递闭包。基本步骤是对于每个(k = 1)到(n),检查对于所有的(i)和(j),如果(M[i][k]=1)且(M[k][j]=1),那么(M[i][j]=1)。
二、Go语言代码实现
package main
import (
"fmt"
)
// calculateTransitiveClosure计算传递闭包
func calculateTransitiveClosure(matrix [][]int) [][]int {
numRows := len(matrix)
numCols := len(matrix[0])
result := make([][]int, numRows)
for i := 0; i < numRows; i++ {
result[i] = make([]int, numCols)
for j := 0; j < numCols; j++ {
result[i][j] = matrix[i][j]
}
}
for k := 0; k < numRows; k++ {
for i := 0; i < numRows; i++ {
for j := 0; j < numRows; j++ {
if result[i][k] == 1 && result[k][j] == 1 {
result[i][j] = 1
}
}
}
}
return result
}
你可以使用以下方式调用这个函数:
func main() {
// 这里是一个简单的示例关系矩阵,你可以根据实际需求替换
relationMatrix := [][]int{
{0, 1, 0},
{0, 0, 1},
{0, 0, 0},
}
transitiveClosure := calculateTransitiveClosure(relationMatrix)
for _, row := range transitiveClosure {
fmt.Println(row)
}
}
请注意,以上代码是基于一般的计算传递闭包的思路,如果25.1节有特殊的算法或者数据结构要求,可能需要进一步调整代码。
chatgpt:
在计算图的传递闭包时,我们可以使用用邻接矩阵或邻接表表示的图的基本算法之一,例如 Floyd-Warshall 算法。这里我将用 Go 语言来演示如何计算传递闭包。
传递闭包的基本思想是,对于图中的每一对顶点,如果存在从顶点 u 到顶点 v 的路径,则在传递闭包中也应该包含一条从 u 到 v 的边。
下面是一个使用 Floyd-Warshall 算法来计算有向图的传递闭包的示例代码。这个算法的时间复杂度是 ( O(V^3) ),其中 V 是图中顶点的数量。
Go 代码示例
package main
import (
"fmt"
"math"
)
// 计算传递闭包
func transitiveClosure(graph [][]bool) [][]bool {
n := len(graph)
// 初始化传递闭包为输入图
closure := make([][]bool, n)
for i := range closure {
closure[i] = make([]bool, n)
copy(closure[i], graph[i])
}
// Floyd-Warshall 算法
for k := 0; k < n; k++ {
for i := 0; i < n; i++ {
for j := 0; j < n; j++ {
closure[i][j] = closure[i][j] || (closure[i][k] && closure[k][j])
}
}
}
return closure
}
func main() {
// 示例图的邻接矩阵表示 (有向图)
graph := [][]bool{
{false, true, false, false},
{false, false, true, false},
{false, false, false, true},
{true, false, false, false},
}
closure := transitiveClosure(graph)
// 打印传递闭包
fmt.Println("传递闭包:")
for _, row := range closure {
for _, val := range row {
if val {
fmt.Print("1 ")
} else {
fmt.Print("0 ")
}
}
fmt.Println()
}
}
代码解释
-
输入图表示:使用邻接矩阵(布尔类型二维切片)来表示图,其中
graph[i][j]为true表示从顶点i到顶点j存在一条边。 -
初始化传递闭包:将输入图复制到
closure矩阵中。 -
Floyd-Warshall 算法:通过三重循环遍历每一对顶点 (i, j),并检查中间顶点 k 的可达性。我们用逻辑或运算符更新闭包矩阵中的每一个值。
-
打印结果:以适当的格式输出传递闭包的结果。
使用示例
运行此代码后,您可以看到传递闭包矩阵的输出,表示图中任意两顶点之间是否可达(1 表示可达,0 表示不可达)。
注意事项
- Floyd-Warshall 算法适合计算传递闭包,但如果图特别大,考虑使用更高效的算法或数据结构(例如深度优先搜索或广度优先搜索)。
kimi:
要使用Go语言计算传递闭包,我们可以参考图论中的算法。传递闭包是一个图的节点集合,其中包含了所有直接和间接的连接关系。在Go语言中,我们可以使用邻接矩阵或邻接列表来表示图,并实现一个算法来计算传递闭包。
以下是一个使用Go语言实现的简单示例,它使用邻接矩阵来表示图,并计算传递闭包:
package main
import "fmt"
// Graph 表示一个有向图
type Graph struct {
V int // 顶点数
Adj [][]int // 邻接矩阵
}
// NewGraph 创建一个新的图
func NewGraph(V int) *Graph {
return &Graph{
V: V,
Adj: make([][]int, V),
}
}
// AddEdge 添加一条边
func (g *Graph) AddEdge(v, w int) {
g.Adj[v] = append(g.Adj[v], w)
}
// TransitiveClosure 计算传递闭包
func (g *Graph) TransitiveClosure() [][]int {
n := g.V
closure := make([][]int, n)
for i := 0; i < n; i++ {
closure[i] = make([]int, n)
for j := 0; j < n; j++ {
if i == j {
closure[i][j] = 1
} else {
closure[i][j] = 0
}
}
}
for k := 0; k < n; k++ {
for i := 0; i < n; i++ {
for j := 0; j < n; j++ {
if g.Adj[i][k] == 1 && g.Adj[k][j] == 1 {
closure[i][j] = 1
}
}
}
}
return closure
}
func main() {
// 创建一个图
g := NewGraph(5)
g.AddEdge(0, 1)
g.AddEdge(0, 2)
g.AddEdge(1, 3)
g.AddEdge(2, 4)
// 计算传递闭包
closure := g.TransitiveClosure()
// 打印传递闭包
for i := 0; i < len(closure); i++ {
for j := 0; j < len(closure[i]); j++ {
if closure[i][j] == 1 {
fmt.Printf("%d -> %d\n", i, j)
}
}
}
}
在这个示例中,我们首先定义了一个Graph结构体来表示图,其中包含了顶点数V和邻接矩阵Adj。NewGraph函数用于创建一个新的图,AddEdge函数用于添加边。TransitiveClosure函数计算传递闭包,它使用三个嵌套循环来更新邻接矩阵,以反映所有直接和间接的连接关系。最后,我们在main函数中创建了一个图,添加了一些边,并计算并打印了传递闭包。
请注意,这个示例是一个简化的版本,它没有考虑性能优化。在实际应用中,可能需要使用更高效的算法,如Floyd-Warshall算法或Tarjan算法,来计算传递闭包。
混元:
在计算机科学中,传递闭包(transitive closure)是一个有向图的属性,它告诉我们在图中从一个节点到另一个节点是否存在路径。换句话说,如果从节点 A 到节点 B 存在一条或多条路径,则在传递闭包中,我们将 A 和 B 视为相连的。
25.1 节的技术可能指的是 Floyd-Warshall 算法,这是一种动态规划算法,用于在加权图中找到最短路径。不过,Floyd-Warshall 算法也可以用来计算无权图的传递闭包,方法是将所有的权重初始化为 0 或 1,并将不存在的边视为权重为无穷大的边。
以下是使用 Go 语言实现的一个简单示例,该示例展示了如何使用类似 Floyd-Warshall 的方法来计算无权图的传递闭包:
package main
import "fmt"
// 初始化图的邻接矩阵表示,这里使用布尔矩阵,true 表示存在边,false 表示不存在边。
func initializeGraph(vertices int, edges [][]int) [][]bool {
graph := make([][]bool, vertices)
for i := range graph {
graph[i] = make([]bool, vertices)
}
for _, edge := range edges {
u, v := edge[0], edge[1]
graph[u][v] = true
}
return graph
}
// 使用类似 Floyd-Warshall 的方法计算传递闭包。
func transitiveClosure(graph [][]bool) [][]bool {
vertices := len(graph)
// 初始化传递闭包矩阵,与图的邻接矩阵相同。
closure := make([][]bool, vertices)
for i := range closure {
closure[i] = make([]bool, vertices)
copy(closure[i], graph[i])
}
// 使用动态规划更新传递闭包矩阵。
for k := 0; k < vertices; k++ {
for i := 0; i < vertices; i++ {
for j := 0; j < vertices; j++ {
closure[i][j] = closure[i][j] || (closure[i][k] && closure[k][j])
}
}
}
return closure
}
func main() {
vertices := 4
edges := [][]int{
{0, 1},
{1, 2},
{2, 3},
}
graph := initializeGraph(vertices, edges)
closure := transitiveClosure(graph)
fmt.Println("Transitive Closure:")
for _, row := range closure {
fmt.Println(row)
}
}
在这个示例中,我们首先初始化了一个布尔矩阵来表示图的邻接矩阵,其中 true 表示两个顶点之间存在一条边。然后,我们使用一个类似 Floyd-Warshall 的动态规划算法来计算传递闭包。最后,我们打印出传递闭包矩阵。
请注意,这个示例假设图是无权的,并且所有的边都是无向的。如果你的图是有权的或者是有向的,你需要对代码进行相应的调整。
- 点赞
- 收藏
- 关注作者


评论(0)