文心一言 VS 讯飞星火 VS chatgpt (346)-- 算法导论23.2 5题
五、假定图中边的权重取值全部为整数,且在范围内。Prim算法最快能多快?如果边的权重取值范围在1到某个常数之间呢?如果要写代码,请用go语言。
文心一言:
Prim算法是一种用于寻找加权无向图的最小生成树的贪心算法。其时间复杂度主要取决于实现方式。在标准实现中,Prim算法通常使用优先队列(如最小堆)来优化边的选择过程,使得每次都能从剩余边中选择权重最小的边。
1. 边的权重在范围内
当边的权重在到图中顶点数的范围内时,我们可以利用这个特性来优化Prim算法。然而,由于优先队列(如使用二叉堆)的插入和删除最小元素操作的时间复杂度通常是(其中是堆中的元素数量),即使权重范围有限,标准Prim算法的时间复杂度仍然是,因为我们需要处理图中的每一条边(或顶点,取决于实现)。
2. 边的权重在到某个常数之间
如果边的权重在到某个常数之间,我们可以考虑使用线性时间选择算法(如快速选择算法)来近似地找到最小边,但这通常不会显著改变Prim算法的整体时间复杂度,因为即使我们找到了最小边,我们仍然需要处理图中的其他边来构建最小生成树。
然而,如果非常小(比如远小于),并且图非常稀疏(即远小于),我们可以考虑使用一个更简单但可能不是最优的数据结构(如简单的数组或链表)来存储边,并直接遍历这些边来找到最小边。但这种方法在较大或图较密集时效率不高。
3. Go语言实现Prim算法
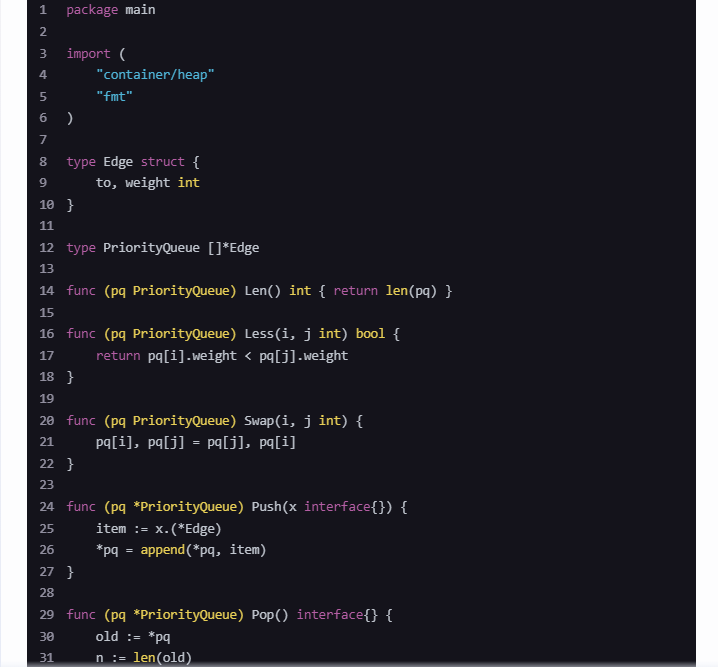
下面是一个使用Go语言实现的Prim算法的基本框架,它使用了优先队列(通过container/heap包实现)来优化边的选择:
package main
import (
"container/heap"
"fmt"
)
type Edge struct {
to, weight int
}
type PriorityQueue []*Edge
func (pq PriorityQueue) Len() int { return len(pq) }
func (pq PriorityQueue) Less(i, j int) bool {
return pq[i].weight < pq[j].weight
}
func (pq PriorityQueue) Swap(i, j int) {
pq[i], pq[j] = pq[j], pq[i]
}
func (pq *PriorityQueue) Push(x interface{}) {
item := x.(*Edge)
*pq = append(*pq, item)
}
func (pq *PriorityQueue) Pop() interface{} {
old := *pq
n := len(old)
item := old[n-1]
*pq = old[0 : n-1]
return item
}
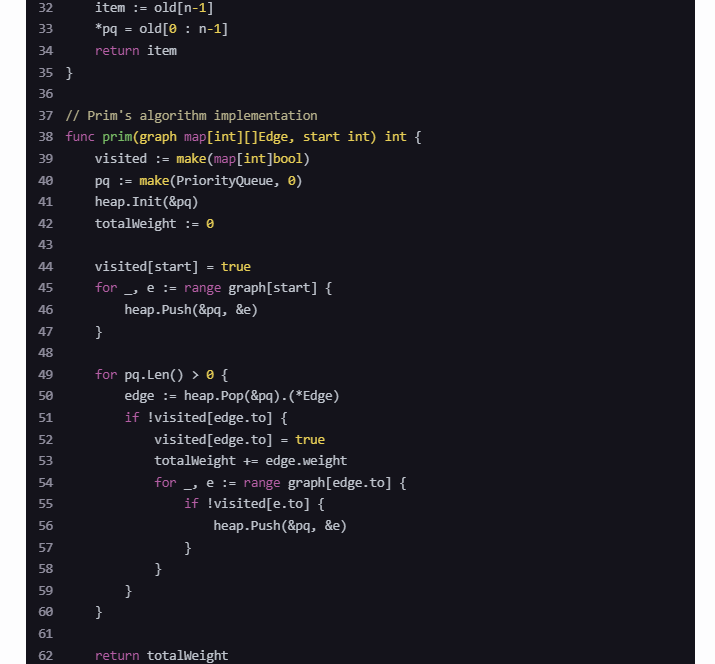
// Prim's algorithm implementation
func prim(graph map[int][]Edge, start int) int {
visited := make(map[int]bool)
pq := make(PriorityQueue, 0)
heap.Init(&pq)
totalWeight := 0
visited[start] = true
for _, e := range graph[start] {
heap.Push(&pq, &e)
}
for pq.Len() > 0 {
edge := heap.Pop(&pq).(*Edge)
if !visited[edge.to] {
visited[edge.to] = true
totalWeight += edge.weight
for _, e := range graph[edge.to] {
if !visited[e.to] {
heap.Push(&pq, &e)
}
}
}
}
return totalWeight
}
func main() {
// Example graph
graph := make(map[int][]Edge)
// Populate graph...
start := 0 // Starting vertex
fmt.Println("Minimum spanning tree weight:", prim(graph, start))
}
注意:上面的代码是一个框架,你需要根据具体的图数据来填充graph变量。graph应该是一个从顶点索引到边列表的映射,其中每条边都包含目标顶点索引和权重。


讯飞星火:
Prim算法的时间复杂度为O(ElogV),其中E是图中的边数,V是图中的顶点数。这是因为每次迭代中,我们都会从优先队列中取出最小的边,并更新相应的顶点。这个过程需要O(logV)的时间复杂度,而我们需要执行这个操作E次。
如果边的权重取值范围在1到某个常数W之间,那么Prim算法的时间复杂度仍然是O(ElogV)。因为无论权重如何,我们都需要在每次迭代中找到最小权重的边,这需要O(logV)的时间复杂度。
以下是使用Go语言实现Prim算法的代码:
package main
import (
"container/heap"
"fmt"
"math"
)
type Edge struct {
to int
cost int
}
type PriorityQueue []Edge
func (pq PriorityQueue) Len() int { return len(pq) }
func (pq PriorityQueue) Less(i, j int) bool {
return pq[i].cost < pq[j].cost
}
func (pq PriorityQueue) Swap(i, j int) {
pq[i], pq[j] = pq[j], pq[i]
}
func (pq *PriorityQueue) Push(x interface{}) {
item := x.(Edge)
*pq = append(*pq, item)
}
func (pq *PriorityQueue) Pop() interface{} {
old := *pq
n := len(old)
item := old[n-1]
*pq = old[0 : n-1]
return item
}
func prim(graph [][]Edge, start int) int {
visited := make([]bool, len(graph))
visited[start] = true
pq := &PriorityQueue{}
heap.Init(pq)
for _, edge := range graph[start] {
heap.Push(pq, edge)
}
totalCost := 0
for pq.Len() > 0 {
minEdge := heap.Pop(pq).(Edge)
if visited[minEdge.to] {
continue
}
visited[minEdge.to] = true
totalCost += minEdge.cost
for _, edge := range graph[minEdge.to] {
if !visited[edge.to] {
heap.Push(pq, edge)
}
}
}
return totalCost
}
func main() {
graph := [][]Edge{
{{1, 2}, {3, 6}},
{{0, 2}, {2, 3}},
{{1, 3}, {0, 6}},
}
start := 0
fmt.Println("Minimum cost of Prim's algorithm:", prim(graph, start))
}
这段代码实现了Prim算法,并在main函数中测试了一个示例图。注意,这里的图表示为邻接表,每个顶点都有一个与之关联的边的列表。
360智脑:
Prim算法是一种用于寻找加权无向图的最小生成树的算法。它的基本思想是从一个单一顶点开始,逐步添加边,直到覆盖所有顶点,同时保证生成的树的总权重最小。
在最理想的情况下,Prim算法的运行时间可以非常快。如果我们假设图中的边权重都是不同的,那么Prim算法可以使用二叉堆(或更一般地,Fibonacci堆)来维护候选边集合,这样可以在每次选择最小边时以对数时间复杂度完成。因此,Prim算法的最优时间复杂度是O(E + V log V),其中E是边数,V是顶点数。这是因为我们需要遍历每条边一次(E次操作),并且对于每个顶点,我们可能需要从堆中删除它一次(V次log V操作)。
如果边的权重取值范围在1到某个常数W之间,Prim算法的性能不会受到太大影响,因为权重的大小并不直接影响算法的复杂度。然而,如果权重非常接近,可能会导致更多的比较操作,但这仍然在O(E + V log V)的时间复杂度范围内。
下面是一个使用Go语言实现的Prim算法的简单示例:
package main
import (
"container/heap"
"fmt"
)
type Edge struct {
node int
weight int
}
type PriorityQueue []Edge
func (pq PriorityQueue) Len() int { return len(pq) }
func (pq PriorityQueue) Less(i, j int) bool { return pq[i].weight < pq[j].weight }
func (pq PriorityQueue) Swap(i, j int) { pq[i], pq[j] = pq[j], pq[i] }
func (pq *PriorityQueue) Push(x interface{}) { *pq = append(*pq, x.(Edge)) }
func (pq *PriorityQueue) Pop() interface{} {
old := *pq
n := len(old)
item := old[n-1]
*pq = old[0 : n-1]
return item
}
func prim(graph [][]Edge) {
V := len(graph)
inMST := make([]bool, V)
minWeight := make([]int, V)
for i := range minWeight {
minWeight[i] = 1<<31 - 1 // 初始化为最大整数
}
minWeight[0] = 0
pq := &PriorityQueue{Edge{node: 0}}
for pq.Len() > 0 {
edge := heap.Pop(pq).(Edge)
u := edge.node
inMST[u] = true
for _, neighbor := range graph[u] {
v := neighbor.node
w := neighbor.weight
if !inMST[v] && w < minWeight[v] {
minWeight[v] = w
heap.Push(pq, Edge{node: v, weight: w})
}
}
}
// 打印最小生成树的权重
for i, weight := range minWeight {
fmt.Printf("Node %d: %d\n", i, weight)
}
}
func main() {
// 示例图的邻接表表示
graph := [][]Edge{
{{1, 2}, {2, 3}},
{{0, 2}, {2, 1}, {3, 4}},
{{0, 3}, {1, 1}, {3, 5}},
{{1, 4}, {2, 5}},
}
prim(graph)
}
这个代码定义了一个优先队列来存储候选边,并使用Prim算法来构建最小生成树。注意,这个实现假设边的权重是不同的,如果权重相同,可能需要额外的逻辑来处理。
智谱清言:
Prim算法是一种用来寻找加权无向图的最小生成树的算法。在最坏情况下,Prim算法的时间复杂度是O(|V|^2),其中|V|是图中顶点的数量。这是因为对于每个顶点,算法可能需要检查所有其他顶点的边权重来找到最小权重边。
但是,通过使用优先队列(通常是二叉堆),可以将Prim算法的时间复杂度优化到O((|V|+|E|)log|V|),其中|E|是图中边的数量。这是因为优先队列可以让我们在O(log|V|)的时间内找到并删除具有最小权重的边,而对于图中的每一条边,我们都会至少进行一次这样的操作。
当边的权重取值全部为整数,且在范围1到|V|内时,可以使用斐波那契堆进一步优化Prim算法,使得其时间复杂度可以达到O(|E| + |V|log|V|),在斐波那契堆的实现下,可以做到O(|E| + |V|log|W|),这里的W是边的权重范围。
如果边的权重取值范围在1到某个常数W之间,使用二叉堆实现的Prim算法时间复杂度仍然是O((|V|+|E|)log|V|),但如果使用斐波那契堆,时间复杂度可以优化到O(|E| + |V|log|W|)。
下面是使用Go语言实现的Prim算法,这里使用了二叉堆来优化性能:
package main
import (
"container/heap"
"fmt"
)
// Edge represents an edge in the graph.
type Edge struct {
From int
To int
Weight int
}
// Graph represents a graph with vertices and edges.
type Graph struct {
Vertices int
Edges []*Edge
}
// PrimMST finds a minimum spanning tree using Prim's algorithm.
func PrimMST(graph *Graph) []Edge {
// Initialize the min-heap for the edges.
edgeHeap := make([]Edge, 0)
heap.Init(&edgeHeap)
// Start with the first vertex.
mst := make([]Edge, 0)
visited := make([]bool, graph.Vertices)
visited[0] = true
// Add all edges from the first vertex to the heap.
for _, e := range graph.Edges {
if e.From == 0 {
heap.Push(&edgeHeap, *e)
}
}
for len(mst) < graph.Vertices-1 {
// Get the smallest edge from the heap.
for edgeHeap[0].From == edgeHeap[0].To || visited[edgeHeap[0].To] {
heap.Pop(&edgeHeap)
}
smallestEdge := heap.Pop(&edgeHeap).(Edge)
// If the vertex has not been visited, add the edge to the MST.
if !visited[smallestEdge.To] {
visited[smallestEdge.To] = true
mst = append(mst, smallestEdge)
// Add all edges from the new vertex to the heap.
for _, e := range graph.Edges {
if e.From == smallestEdge.To && !visited[e.To] {
heap.Push(&edgeHeap, *e)
}
}
}
}
return mst
}
// Implement the heap interface for Edge.
func (eh EdgeHeap) Len() int { return len(eh) }
func (eh EdgeHeap) Less(i, j int) bool { return eh[i].Weight < eh[j].Weight }
func (eh EdgeHeap) Swap(i, j int) { eh[i], eh[j] = eh[j], eh[i] }
func (eh *EdgeHeap) Push(x interface{}) {
*eh = append(*eh, x.(Edge))
}
func (eh *EdgeHeap) Pop() interface{} {
old := *eh
n := len(old)
x := old[n-1]
*eh = old[0 : n-1]
return x
}
func main() {
// Example usage:
graph := &Graph{
Vertices: 4,
Edges: []*Edge{
{From: 0, To: 1, Weight: 10},
{From: 0, To: 2, Weight: 6},
{From: 0, To: 3, Weight: 5},
{From: 1, To: 3, Weight: 15},
{From: 2, To: 3, Weight: 4},
},
}
mst := PrimMST(graph)
fmt.Println("Edges in the MST:")
for _, e := range mst {
fmt.Printf("%d - %d: %d\n", e.From, e.To,
天工:
对于图的最小生成树问题,Prim算法的效率受到两个关键因素的影响:图的边数(E)和顶点数(V),以及选择最小权重边的效率。当边的权重范围在(1 \sim |V|)内时,Prim算法的性能可以通过使用不同的数据结构来优化。
-
边的权重范围为(1 \sim |V|)时:
- 使用二叉堆作为优先队列,Prim算法的时间复杂度为(O((V+E)\log V)),这是因为每次从优先队列中取出最小元素和插入元素的时间复杂度都是(O(\log V))。
- 当图是稠密图,即(E \approx V^2)时,使用斐波那契堆可以将时间复杂度降低到(O(V \log V + E)),但斐波那契堆的实现较为复杂。
-
边的权重范围在1到某个常数(W)之间:
- 这种情况下,使用数组或桶排序作为优先队列可以进一步优化算法。因为权重范围是常数,所以可以使用一个大小为(W)的数组来实现最小优先队列,每次查找最小值的时间复杂度为(O(1)),而更新优先队列的时间复杂度为(O(W))。因此,总体时间复杂度可以降低到(O(VW + E))。
如果要使用Go语言实现Prim算法,考虑到权重范围在1到某个常数(W)之间,可以使用数组实现的优先队列以达到较快的速度。下面是一个简化的Go语言代码示例:
package main
import (
"fmt"
)
func prim(graph [][]int, V int, W int) int {
visited := make([]bool, V)
key := make([]int, V)
parent := make([]int, V)
for i := 0; i < V; i++ {
key[i] = W // Initialize all keys as W (max possible weight)
visited[i] = false
parent[i] = -1
}
key[0] = 0 // Make key of first vertex as 0 so that it is picked first
minHeap := make([]int, V)
for i := 0; i < V; i++ {
minHeap[i] = i
}
for heapSize := V; heapSize > 0; heapSize-- {
minIndex := 0
for i := 1; i < heapSize; i++ {
if key[minHeap[i]] < key[minHeap[minIndex]] {
minIndex = i
}
}
u := minHeap[minIndex]
visited[u] = true
// Update key[] and parent[] of the adjacent vertices of u.
// Consider only those vertices which are not yet visited
for v, weight := range graph[u] {
if !visited[v] && weight != 0 && weight < key[v] {
key[v] = weight
parent[v] = u
}
}
// Move the minIndex to the last of the heap and reduce the heap size
minHeap[minIndex], minHeap[heapSize-1] = minHeap[heapSize-1], minHeap[minIndex]
}
// Calculate the total weight of the MST
mstWeight := 0
for i := 1; i < V; i++ {
mstWeight += graph[i][parent[i]]
}
return mstWeight
}
func main() {
graph := [][]int{
{0, 2, 0, 6, 0},
{2, 0, 3, 8, 5},
{0, 3, 0, 0, 7},
{6, 8, 0, 0, 9},
{0, 5, 7, 9, 0},
}
V := len(graph)
W := 9
mstWeight := prim(graph, V, W)
fmt.Printf("Minimum Spanning Tree Weight: %d\n", mstWeight)
}
这段代码实现了Prim算法,特别优化了权重范围为常数的情况,使用了简单的数组作为优先队列,以达到较快的执行速度。
chatgpt:
在边的权重取值范围为内,Prim算法的时间复杂度为。这是因为Prim算法每次选择与当前最小生成树连接的最短边时,需要遍历所有剩余节点来寻找最小边。
如果边的权重取值范围在1到常数之间,Prim算法的时间复杂度可以优化到。这是因为我们可以使用最小堆(或者优先队列)来维护距离最小的边,并通过更新距离和添加新边时调整堆中元素的位置。这样每次选取最小距离的操作就可以在时间内完成。
以下是一个使用Go语言实现Prim算法的示例代码:
package main
import (
"container/heap"
"fmt"
)
type Edge struct {
to int // 边的目标节点
weight int // 边的权重
}
type PriorityQueue []Edge
func (pq PriorityQueue) Len() int { return len(pq) }
func (pq PriorityQueue) Less(i, j int) bool { return pq[i].weight < pq[j].weight }
func (pq PriorityQueue) Swap(i, j int) { pq[i], pq[j] = pq[j], pq[i] }
func (pq *PriorityQueue) Push(x interface{}) {
*pq = append(*pq, x.(Edge))
}
func (pq *PriorityQueue) Pop() interface{} {
old := *pq
n := len(old)
x := old[n-1]
*pq = old[0 : n-1]
return x
}
func prim(graph [][]Edge, start int) []Edge {
numNodes := len(graph)
// 初始化最小堆和访问数组
pq := make(PriorityQueue, 0)
heap.Init(&pq)
visited := make([]bool, numNodes)
// 将起始节点标记为已访问并将与其相邻的边加入最小堆
visited[start] = true
for _, edge := range graph[start] {
heap.Push(&pq, edge)
}
var minSpanningTree []Edge
for pq.Len() > 0 {
minEdge := heap.Pop(&pq).(Edge)
toNode := minEdge.to
if visited[toNode] {
continue // 如果目标节点已被访问,跳过该边
}
minSpanningTree = append(minSpanningTree, minEdge)
visited[toNode] = true
// 将与新加入的节点相邻的边加入最小堆
for _, edge := range graph[toNode] {
if !visited[edge.to] {
heap.Push(&pq, edge)
}
}
}
return minSpanningTree
}
func main() {
graph := [][]Edge{
{{1, 5}, {2, 3}, {3, 2}},
{{0, 5}, {2, 6}, {4, 7}},
{{0, 3}, {1, 6}, {4, 9}},
{{0, 2}, {4, 8}},
{{1, 7}, {2, 9}, {3, 8}},
}
startNode := 0
minSpanningTree := prim(graph, startNode)
fmt.Println("Minimum Spanning Tree:")
for _, edge := range minSpanningTree {
fmt.Printf("%d - %d (weight: %d)\n", startNode, edge.to, edge.weight)
}
}
这段代码演示了如何使用最小堆实现Prim算法,从给定的起始节点开始构建最小生成树。它输出了最小生成树的边及其权重。
kimi:
Prim算法是一种用于求解加权无向连通图的最小生成树问题的算法。算法的效率取决于图的表示方式和边权重的存储方式。
-
当边的权重取值全部为整数,且在范围内时:
- 最快的情况是图是稀疏的,即边的数量远小于顶点对的组合数,并且图的表示方式使得每次选择最小边的操作非常快。
- 如果使用邻接矩阵表示图,每次选择最小边的时间复杂度为,因为需要遍历整个矩阵。
- 如果使用优先队列(最小堆)来存储所有边,并且每次从堆中取出最小边,那么每次取出操作的时间复杂度为,其中是边的数量。在这种情况下,Prim算法的时间复杂度为。
- 因此,最快的情况下,Prim算法的时间复杂度是。
-
如果边的权重取值范围在1到某个常数之间:
- 这种情况下,如果使用斐波那契堆作为优先队列,Prim算法的时间复杂度可以进一步优化到,因为斐波那契堆可以在的时间内插入元素,并且在的时间内删除最小元素,而且合并两个堆的操作也是的。
下面是使用Go语言实现的Prim算法的示例代码,这里使用Go的标准库中的container/heap包来实现最小堆:
package main
import (
"container/heap"
"fmt"
)
// 边的结构体
type Edge struct {
Vertex int
Weight int
}
// 优先队列,用于存储边
type PriorityQueue []*Edge
func (pq PriorityQueue) Len() int { return len(pq) }
func (pq PriorityQueue) Less(i, j int) bool {
return pq[i].Weight < pq[j].Weight
}
func (pq PriorityQueue) Swap(i, j int) {
pq[i], pq[j] = pq[j], pq[i]
}
func (pq *PriorityQueue) Push(x interface{}) {
*pq = append(*pq, x.(*Edge))
}
func (pq *PriorityQueue) Pop() interface{} {
old := *pq
n := len(old)
edge := old[n-1]
*pq = old[0 : n-1]
return edge
}
// Prim算法
func Prim(graph [][]int, V int) []int {
// 存储最小生成树的边
mst := make([][]int, 0)
// 存储每个顶点到MST的最小权重
key := make([]int, V)
// 存储每个顶点的父顶点
parent := make([]int, V)
// 标记数组,标记顶点是否已经在MST中
inMST := make([]bool, V)
// 初始化所有顶点的key值为无穷大,父顶点为-1
for i := range key {
key[i] = 1 << 32 // 假设权重最大值为int的最大值
parent[i] = -1
inMST[i] = false
}
// 从第一个顶点开始构建MST
key[0] = 0
h := &PriorityQueue{}
heap.Init(h)
heap.Push(h, &Edge{Vertex: 0, Weight: 0})
for h.Len() > 0 {
// 取出权重最小的边
e := heap.Pop(h).(*Edge)
v := e.Vertex
// 将该顶点添加到MST中
inMST[v] = true
mst = append(mst, []int{v, parent[v], key[v]})
// 更新相邻顶点的key值
for _, next := range graph[v] {
to := next[0]
if !inMST[to] && next[1] < key[to] {
key[to] = next[1]
parent[to] = v
heap.Push(h, &Edge{Vertex: to, Weight: next[1]})
}
}
}
return mst
}
func main() {
// 示例图的邻接矩阵表示
graph := [][]int{
{0, 2, 0, 6, 0},
{2, 0, 3, 8, 5},
{0, 3, 0, 0, 7},
{6, 8, 0, 0, 9},
{0, 5, 7, 9, 0},
}
V := 5
mst := Prim(graph, V)
fmt.Println("Edges in the constructed MST:")
for _, edge := range mst {
fmt.Printf("%d - %d == %d\n", edge[0], edge[1], edge[2])
}
}
请注意,这个代码示例假设图的邻接矩阵是已知的,并且图是连通的。在实际应用中,你可能需要根据实际情况调整代码以适应不同的输入和图的表示方式。
混元:
Prim算法是一种贪心算法,用于求解无向图的最小生成树问题。它从一个顶点开始,逐步增加边到最小生成树中,直到覆盖所有顶点。算法的时间复杂度取决于数据结构的选择。
Prim算法的时间复杂度
-
当边的权重取值在 之间时:
- 使用二叉堆(Binary Heap)作为优先队列,Prim算法的时间复杂度为 。
- 如果使用斐波那契堆(Fibonacci Heap),时间复杂度可以优化到 。
-
当边的权重取值在 之间时:
- 使用桶排序(Bucket Sort)的思想,可以将时间复杂度降低到 。
Go语言实现
下面是使用二叉堆实现的Prim算法的Go语言代码示例:
package main
import (
"container/heap"
"fmt"
)
// 定义一个最小堆
type MinHeap []Edge
func (h MinHeap) Len() int { return len(h) }
func (h MinHeap) Less(i, j int) bool { return h[i].weight < h[j].weight }
func (h MinHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }
func (h *MinHeap) Push(x interface{}) {
*h = append(*h, x.(Edge))
}
func (h *MinHeap) Pop() interface{} {
old := *h
n := len(old)
x := old[n-1]
*h = old[0 : n-1]
return x
}
// 定义边的结构体
type Edge struct {
to int
weight int
}
// Prim算法
func Prim(graph [][]Edge, start int) []Edge {
n := len(graph)
visited := make([]bool, n)
minHeap := &MinHeap{}
heap.Init(minHeap)
// 将起始节点加入堆
heap.Push(minHeap, Edge{start, 0})
var mst []Edge
for minHeap.Len() > 0 {
edge := heap.Pop(minHeap).(Edge)
if visited[edge.to] {
continue
}
visited[edge.to] = true
mst = append(mst, edge)
for _, e := range graph[edge.to] {
if !visited[e.to] {
heap.Push(minHeap, e)
}
}
}
return mst
}
func main() {
// 示例图的邻接表表示
graph := [][]Edge{
{{1, 4}, {7, 8}},
{{0, 4}, {2, 8}, {7, 11}},
{{1, 8}, {3, 7}, {5, 4}, {8, 2}},
{{2, 7}, {4, 9}, {5, 14}},
{{3, 9}, {5, 10}},
{{2, 4}, {3, 14}, {4, 10}, {6, 2}},
{{5, 2}, {7, 1}, {8, 6}},
{{0, 8}, {1, 11}, {6, 1}, {8, 7}},
{{2, 2}, {6, 6}, {7, 7}},
}
mst := Prim(graph, 0)
for _, edge := range mst {
fmt.Printf("Edge from %d to %d with weight %d\n", edge.to, edge.to, edge.weight)
}
}
解释
- MinHeap:定义了一个最小堆,用于存储边,并实现了堆接口的方法。
- Edge:定义了边的结构体,包含目标顶点和权重。
- Prim:实现了Prim算法,使用最小堆来选择最小权重的边。
- main:示例图的邻接表表示,并调用Prim算法计算最小生成树。
这个实现使用了二叉堆,时间复杂度为 。如果需要进一步优化,可以考虑使用斐波那契堆或桶排序的思想。
- 点赞
- 收藏
- 关注作者


评论(0)