基于离散差分法的复杂微分方程组求解matlab数值仿真

1.程序功能描述
      基于离散差分法的复杂微分方程组求解.“连续微分方程”到“离散微分方程”到“差分方程”，离散微分方程，变成差分方程。建立差分方程时，时间采用一阶显格式，空间采用一阶偏心差分格式。

2.测试软件版本以及运行结果展示
MATLAB2022a版本运行

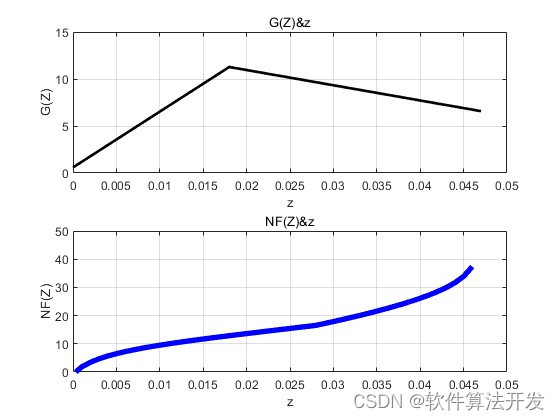
3.核心程序

%         ʼ  
L       = 0.05;   % ռ䳤  
time    = 1e-8;   %ʱ 䳤  
Nz      = 10;    % ռ    
Nt      = 10;    %ʱ        
dt      = time/Nt;%t΢ ֵ    ۼ   
dz      = L/Nz;%z΢ ֵ    ۼ   
 
N1         = zeros(Nz,Nt);
N2         = zeros(Nz,Nt);
N3         = zeros(Nz,Nt);
N4         = zeros(Nz,Nt);
N1_Yb      = zeros(Nz,Nt);
N2_Yb      = zeros(Nz,Nt);
Ps         = zeros(Nz,Nt);
 
PASE_plus  = zeros(M,Nz,Nt);
PASE_minus = zeros(M,Nz,Nt);
Pp_plus    = zeros(Nz,Nt);
Pp_minus   = zeros(Nz,Nt);
 
G          = zeros(Nz,Nt);
NF         = zeros(Nz,Nt);
 
%      1  ʽ  1    ϵ   IJ     ʾ
W11 = Fp*O13_vp/(Ac*h*Vp);
W12 = Fs*O12_vs/(Ac*h*Vs);
for i = 1:M
    W13(i) = F_ASE_vj(i) * O12_vj(i) / (Ac*h*Vj(i));
end
 
W14 = Fs*O21_vs/(Ac*h*Vs);
for i = 1:M
    W15(i) = F_ASE_vj(i) * O21_vj(i) / (Ac*h*Vj(i));
end
 
W16 = Fp*O31_vp/(Ac*h*Vp);
 
%      1  ʽ  2    ϵ   IJ     ʾ
W21 = Fs*O12_vs/(Ac*h*Vs);
 
for i = 1:M
    W22(i) = F_ASE_vj(i) * O12_vj(i) / (Ac*h*Vj(i));
end
W23 = Fs*O21_vs/(Ac*h*Vs);
 
for i = 1:M
    W24(i) = F_ASE_vj(i) * O21_vj(i) / (Ac*h*Vj(i));
end
 
%      1  ʽ  3    ϵ   IJ     ʾ
W31 = Fp*O13_vp/(Ac*h*Vp); 
W32 = Fp*O31_vp/(Ac*h*Vp); 
 
%      1  ʽ  4    ϵ   IJ     ʾ
W41           = Fp*O12Yb_vp/(Ac*h*Vp);
W42           = Fp*O21Yb_vp/(Ac*h*Vp);
Ps(1,:)       = 0.001*ones(1,Nt);
Pp_plus(1,:)  = 0.06*ones(1,Nt);
Pp_minus(1,:) = 0.04*ones(1,Nt);
 
for j = 1:Nt-1
    for i = 1:Nz-1
        %      1ʽ  1
        N1(i,j+1) = N1(i,j) + ...
                    dt*( -1*(W11*(Pp_plus(i,j) + Pp_minus(i,j)) + W12*Ps(i,j) + sum(W13.*(PASE_plus(:,i,j)+PASE_minus(:,i,j))'))*N1(i,j) +...
                            (A21 + W14*Ps(i,j) + sum(W15.*(PASE_plus(:,i,j)+PASE_minus(:,i,j))'))*N2(i,j) + ...
                             C2*N2(i,j)^2 + W16*(Pp_plus(i,j) + Pp_minus(i,j))*N3(i,j) + C3*N3(i,j)^2 - C14*N1(i,j)*N4(i,j)+...
                            -1*Ktr*N2_Yb(i,j)*N1(i,j)+Kba*N1_Yb(i,j)*N3(i,j) );
    
        %      1ʽ  2
        N2(i,j+1) = N2(i,j) + ...   
                    dt*( (W21*Ps(i,j)+sum(W22.*(PASE_plus(:,i,j)+PASE_minus(:,i,j))'))*N1(i,j) +...
                      -1*(A21 + W23*Ps(i,j) + sum( W24.*(PASE_plus(:,i,j)+PASE_minus(:,i,j))' ))*N2(i,j) +...
                          A32*N3(i,j) - 2*C2*N2(i,j)^2 + 2*C14*N1(i,j)*N4(i,j) );
        
        %      1ʽ  3
        N3(i,j+1) = N3(i,j) + ...    
                    dt*( W31*(Pp_plus(i,j) + Pp_minus(i,j))*N1(i,j) - A32*N3(i,j) - W32*(Pp_plus(i,j) + Pp_minus(i,j))*N3(i,j) -...
                         2*C3*N3(i,j)^2 + A43*N4(i,j) + Ktr*N2_Yb(i,j)*N1(i,j) - Kba*N1_Yb(i,j)*N3(i,j) );
       
        %      1ʽ  4
        N1_Yb(i,j+1) = N1_Yb(i,j) + ...
                       dt*(-1*W41*(Pp_plus(i,j) + Pp_minus(i,j))*N1_Yb(i,j) + W42*(Pp_plus(i,j) + Pp_minus(i,j))*N2_Yb(i,j) +...
                              A21Yb*N2_Yb(i,j) + Ktr*N2_Yb(i,j)*N1(i,j) - Kba*N1_Yb(i,j)*N3(i,j));
                
        %      1ʽ  5
        N4(i,j+1) = NEr - (N1(i,j+1) + N2(i,j+1) + N3(i,j+1)); 
        
        %      1ʽ  6
        N2_Yb(i,j+1) = NYb - N1_Yb(i,j+1);
        
        if N1(i,j+1) > NEr,N1(i,j+1) = NEr;end
        if N2(i,j+1) > NEr,N2(i,j+1) = NEr;end    
        if N3(i,j+1) > NEr,N3(i,j+1) = NEr;end    
        if N4(i,j+1) > NEr,N4(i,j+1) = NEr;end    
        if N1_Yb(i,j+1) > NYb,N1_Yb(i,j+1) = NYb;end
        if N2_Yb(i,j+1) > NYb,N2_Yb(i,j+1) = NYb;end          
        
        if N1(i,j+1) < 0,N1(i,j+1) = 0;end
        if N2(i,j+1) < 0,N2(i,j+1) = 0;end    
        if N3(i,j+1) < 0,N3(i,j+1) = 0;end    
        if N4(i,j+1) < 0,N4(i,j+1) = 0;end    
        if N1_Yb(i,j+1) < 0,N1_Yb(i,j+1) = 0;end
        if N2_Yb(i,j+1) < 0,N2_Yb(i,j+1) = 0;end             
        
  
        %     Ϸ  ̼   õ   N1  N2  N3  N4  N1Yb  N2Yb    
        %      2
        Pp_plus(i+1,j)   =  Pp_plus(i,j)  + dz*(-Fp*(O13_vp*N1(i,j) - O31_vp*N3(i,j) + O12Yb_vp*N1_Yb(i,j) - O21Yb_vp*N2_Yb(i,j))*Pp_plus(i,j)  - ap*Pp_plus(i,j));
 
        Pp_minus(i+1,j)  =  Pp_minus(i,j) + dz*(Fp*(O13_vp*N1(i,j) - O31_vp*N3(i,j) + O12Yb_vp*N1_Yb(i,j) - O21Yb_vp*N2_Yb(i,j))*Pp_minus(i,j) + ap*Pp_plus(i,j));
 
        Ps(i+1,j)        =  Ps(i,j)     + dz*(Fs*( O21_vs*N2(i,j) - O12_vs*N1(i,j) )*Ps(i,j) - as*Ps(i,j)); 
    
        for ii = 1:M
            PASE_plus(ii,i+1,j)  =    PASE_plus(ii,i,j)+dz*(F_ASE_vj(ii)*( O21_vj(ii)*N2(i,j) - O12_vj(ii)*N1(i,j) ) * PASE_plus(ii,i,j) +...
                                      2*h*Vj(ii)*DVj(ii)*F_ASE_vj(ii)*O21_vj(ii)*N2(i,j)-as*PASE_plus(ii,i,j));
 
            PASE_minus(ii,i+1,j) =   PASE_minus(ii,i,j)+dz*(-1*F_ASE_vj(ii)*( O21_vj(ii)*N2(i,j) - O12_vj(ii)*N1(i,j) ) * PASE_minus(ii,i,j) -...
                                     2*h*Vj(ii)*DVj(ii)*F_ASE_vj(ii)*O21_vj(ii)*N2(i,j)+as*PASE_minus(ii,i,j));            
        end
 
        if Pp_plus(i+1,j)    < 0,Pp_plus(i+1,j)     = 0;end
        if Pp_minus(i+1,j)   < 0,Pp_minus(i+1,j)    = 0;end
        if Ps(i+1,j)         < 0,Ps(i+1,j)          = 0;end        
 
        %ͨ    ̬    õ Pp+  Pp-  Pase+  Pase-  Ps
        
    end
end
 
for z = 1:Nz
    for t = 1:Nt
        PASE_plus2(z,t)  = sum(PASE_plus(:,z,t));
        PASE_minus2(z,t) = sum(PASE_minus(:,z,t));
    end
end
 
for z = 1:Nz
    for t = 1:Nt
        G(z,t)  =  10*log10(Ps(z,t)/Ps(1,1)); 
    end
end
 
for z = 1:Nz
    for t = 1:Nt
        NF(z,t)  =  10*log10(1/G(z,t) +  PASE_plus2(z,t)/(G(z,t)*Vs*DVs) ); 
    end
end
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Pp_plus2  = interp1(dz:dz:L,Pp_plus(1:end,Nz),0:dz/10:L,'cubic');
Pp_minus2 = interp1(dz:dz:L,Pp_minus(1:end,Nz),0:dz/10:L,'cubic');
 
figure;
subplot(211);
plot(0:dz/10:L,Pp_plus2,'g-','LineWidth',3);
xlabel('z');
ylabel('Pp+(Z)');
title('Pp+(Z)&z');
grid on;
subplot(212);
plot(L:-dz/10:0,Pp_minus2,'m--','LineWidth',2);
xlabel('z');
ylabel('Pp-(Z)');
title('Pp-(Z)&z');
grid on;
16_015m

4.本算法原理
本课题求解的方程组表达式如下：

    基于离散差分法的复杂微分方程组求解.“连续微分方程”到“离散微分方程”到“差分方程”，离散微分方程，变成差分方程。建立差分方程时，时间采用一阶显格式，空间采用一阶偏心差分格式。