哈希表是一种重要的数据结构，常用于提高数据查找、插入和删除的效率。它结合了数组和哈希函数的特点，以实现快速的数据存取。哈希表是一个功能强大且灵活的数据结构，适用于需要快速查找、插入和删除的场景。了解其基本原理、操作和优缺点，能够帮助你在适合的场景中应用哈希表，提高程序的性能。下面是对哈希表的详细介绍：

哈希表的基本概念

1. 哈希函数：

   • 哈希表的核心是哈希函数（Hash Function），它将输入的键（key）映射到哈希表中一个特定的位置（即数组的索引）。
   • 理想的哈希函数能够将不同的键均匀地分布到数组中，以减少冲突（即不同的键产生相同的哈希值）。

2. 数组：

   • 哈希表通常使用数组作为底层存储结构，因为数组可以在常数时间内访问特定索引的元素。
   • 数组的大小通常是一个质数，以减少碰撞，并提高哈希表的空间利用效率。

3. 冲突处理：

   • 链表法：在哈希表的每个槽中使用一个链表来存储所有哈希值相同的元素。
   • 开放地址法：在哈希表中查找下一个空槽以存储冲突的元素，常见的探查方式有线性探查、二次探查和双重哈希。

哈希表的操作

1. 插入：

   • 使用哈希函数计算键的哈希值，确定在数组中的位置。如果该位置已经被占用，与碰撞处理策略配合，将新元素插入到合适的位置。

2. 查找：

   • 根据键计算哈希值，查找对应位置的数据。如果发生碰撞，根据设置的处理策略依次查找。

3. 删除：

   • 先查找元素，找到后根据具体的冲突处理策略删除元素，并可能需要调整其他元素的位置。

哈希表的优缺点

优点：

• 时间复杂度：平均情况下，插入、查找和删除操作的时间复杂度为 O(1)。
• 适合频繁的查找和插入操作。

缺点：

• 最坏情况下（如大量冲突发生），时间复杂度可能退化为 O(n)。
• 需要合理设计哈希函数与冲突处理策略，以提高效率和减少冲突。
• 当数据量超出哈希表容量时，需要扩展数组，这可能导致性能下降。

那么，话不多说，我们直接看题：

题目一：

2869.收集元素的最少操作次数【简单】

题目：

给你一个正整数数组 nums 和一个整数 k 。

一次操作中，你可以将数组的最后一个元素删除，将该元素添加到一个集合中。

请你返回收集元素 1, 2, ..., k 需要的 最少操作次数 。

示例 1：

输入：nums = [3,1,5,4,2], k = 2
输出：4
解释：4 次操作后，集合中的元素依次添加了 2 ，4 ，5 和 1 。此时集合中包含元素 1 和 2 ，所以答案为 4 。

示例 2：

输入：nums = [3,1,5,4,2], k = 5
输出：5
解释：5 次操作后，集合中的元素依次添加了 2 ，4 ，5 ，1 和 3 。此时集合中包含元素 1 到 5 ，所以答案为 5 。

示例 3：

输入：nums = [3,2,5,3,1], k = 3
输出：4
解释：4 次操作后，集合中的元素依次添加了 1 ，3 ，5 和 2 。此时集合中包含元素 1 到 3  ，所以答案为 4 。

提示：

• 1 <= nums.length <= 50
• 1 <= nums[i] <= nums.length
• 1 <= k <= nums.length
• 输入保证你可以收集到元素 1, 2, ..., k 。

分析问题：

        这个题的数据量并不是很大，所以我们可以使用pop函数以及index函数求解，并不会造成超时。分析问题，问题要求我们从后往前遍历，寻找最少操作次数，如果不熟练从后往前的话，我们可以在最开始就把nums数组给翻过来，这样我们从前找。

        定义一个列表ls,里面放1~k这几个正整数，然后从前开始遍历，这里我们不知道会遍历多少次，所以使用while循环，当ls为空的时候退出循环。定义一个指针re代表nums数组的下标，k代表操作次数。遍历过程中遇到存在ls里面的元素则ls.pop该元素，re,k都加等于1。最后返回结果k即可。

代码实现：

class Solution:
    def minOperations(self, nums: List[int], k: int) -> int:
        nums=nums[::-1]
        la=[x for x in range(1,k+1)]
        re,k=0,0
        while la:
            if nums[re] in la:
                la.pop(la.index(nums[re]))
            k+=1
            re+=1
        return k

​

 题目二：

3194.最小元素和最大元素的最小平均值【简单】

题目：

你有一个初始为空的浮点数数组 averages。另给你一个包含 n 个整数的数组 nums，其中 n 为偶数。

你需要重复以下步骤 n / 2 次：

• 从 nums 中移除 最小 的元素 minElement 和 最大 的元素 maxElement。
• 将 (minElement + maxElement) / 2 加入到 averages 中。

返回 averages 中的 最小 元素。

示例 1：

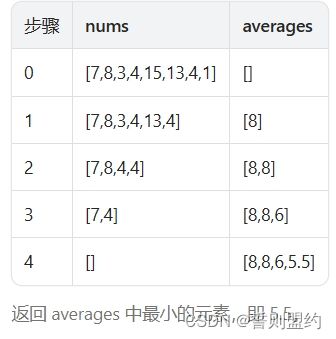
输入： nums = [7,8,3,4,15,13,4,1]

输出： 5.5

解释：

​

示例 2：

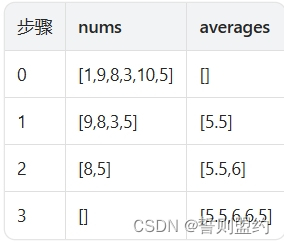
输入： nums = [1,9,8,3,10,5]

输出： 5.5

解释：

示例 3：

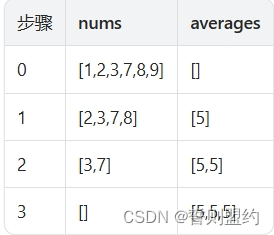
输入： nums = [1,2,3,7,8,9]

输出： 5.0

解释：

提示：

• 2 <= n == nums.length <= 50
• n 为偶数。
• 1 <= nums[i] <= 50

​

 分析问题：

    这道题也不难，步骤大致分为以下四步：

1. 初始化：

   • 初始化结果变量 re 为 0，用于遍历列表。
   • 初始化最小平均值变量 a_min 为一个较大值（100），用于后续比较更新。
   • 计算列表长度并保存到变量 n 。

2. 排序列表：对输入的 nums 列表进行排序，这样在后续计算平均值时，可以方便地从两端选取元素。

3. 循环计算与比较：

   • 通过一个循环，每次从已排序的列表两端选取元素，计算它们的平均值 key 。
   • 将计算得到的平均值 key 与当前的最小平均值 a_min 进行比较，如果 key 更小，则更新 a_min 。
   • 然后移动起始和结束索引，继续下一轮的计算和比较。

4. 返回结果：循环结束后，返回最终得到的最小平均值 a_min 。

        其核心思想是通过遍历列表两端元素的组合，计算平均值并找到其中的最小值。

 代码实现：

class Solution:
    def minimumAverage(self, nums: List[int]) -> float:
        re,a_min,n=0,100,len(nums)-1
        nums.sort()
        while re<=n:
            key=(nums[re]+nums[n])/2
            a_min=min(a_min,key)
            re+=1
            n-=1
        return a_min

总结：

考点：

1. 列表的操作，包括反转列表、元素的访问和修改。
2. 集合或列表的包含关系判断和元素删除操作。
3. 循环结构的使用，通过条件判断控制循环的执行。

收获：

1. 学会如何通过切片操作 [::-1] 快速反转列表。
2. 掌握一种通过循环和条件判断来处理列表中元素匹配和删除的方法。
3. 理解如何在循环中动态地根据条件更新相关变量，以达到求解问题的目的。
4. 提高对逻辑判断和控制流程的理解和运用能力。

“点亮星火，眺望未来。”——《星火集》