文心一言 VS 讯飞星火 VS chatgpt （302）-- 算法导论22.1 6题

举报
福大大架构师每日一题 发表于 2024/07/14 20:20:53 2024/07/14
【摘要】 六、多数以邻接矩阵作为输人的图算法的运行时间为Ω(V2)Ω(V^{2})Ω(V2)，但也有例外。给定图GGG的邻接矩阵表示，请给出一个O(V)O(V)O(V)时间的算法来判断有向图GGG是否存在一个通用汇点(universal sink)。通用汇点指的是入度为∣V∣−1|V|-1∣V∣−1但出度为 0 的结点。如果要写代码，请用go语言。 文心一言：要判断一个有向图是否存在一个通用汇点（u...

六、多数以邻接矩阵作为输人的图算法的运行时间为Ω(V2)Ω(V^{2})，但也有例外。给定图GG的邻接矩阵表示，请给出一个O(V)O(V)时间的算法来判断有向图GG是否存在一个通用汇点(universal sink)。通用汇点指的是入度为∣V∣−1|V|-1但出度为 0 的结点。如果要写代码，请用go语言。

文心一言：

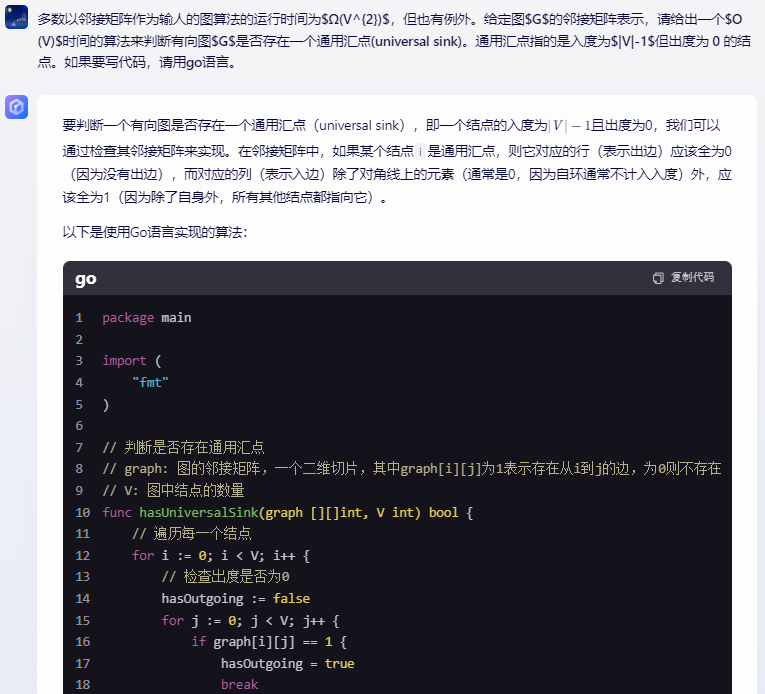
要判断一个有向图是否存在一个通用汇点（universal sink），即一个结点的入度为∣V∣−1|V|-1且出度为0，我们可以通过检查其邻接矩阵来实现。在邻接矩阵中，如果某个结点i是通用汇点，则它对应的行（表示出边）应该全为0（因为没有出边），而对应的列（表示入边）除了对角线上的元素（通常是0，因为自环通常不计入入度）外，应该全为1（因为除了自身外，所有其他结点都指向它）。

以下是使用Go语言实现的算法：

package main

import (
    "fmt"
)

// 判断是否存在通用汇点
// graph: 图的邻接矩阵，一个二维切片，其中graph[i][j]为1表示存在从i到j的边，为0则不存在
// V: 图中结点的数量
func hasUniversalSink(graph [][]int, V int) bool {
    // 遍历每一个结点
    for i := 0; i < V; i++ {
        // 检查出度是否为0
        hasOutgoing := false
        for j := 0; j < V; j++ {
            if graph[i][j] == 1 {
                hasOutgoing = true
                break
            }
        }
        if hasOutgoing {
            // 如果发现有出边，则当前结点不可能是通用汇点
            continue
        }

        // 检查入度是否为V-1
        inDegree := 0
        for j := 0; j < V; j++ {
            if i != j && graph[j][i] == 1 {
                inDegree++
            }
        }
        if inDegree == V-1 {
            // 找到通用汇点
            return true
        }
    }

    // 没有找到通用汇点
    return false
}

func main() {
    // 示例邻接矩阵
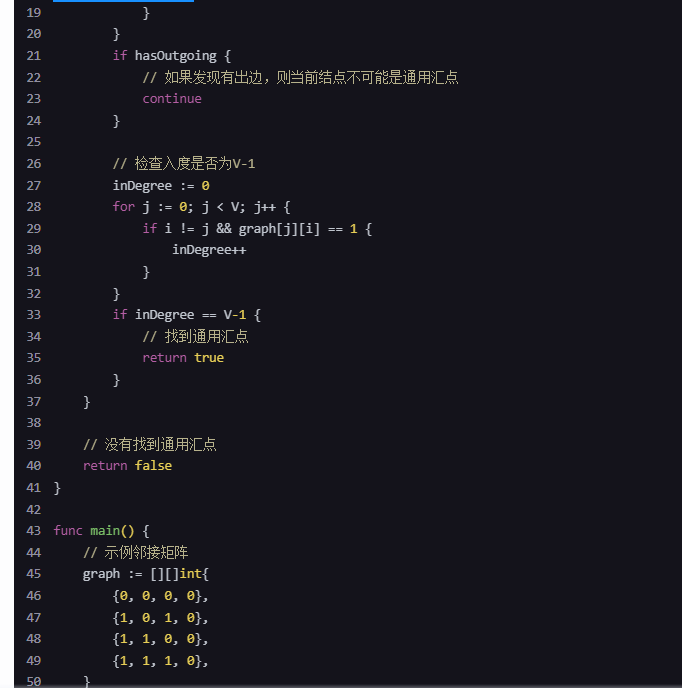
    graph := [][]int{
        {0, 0, 0, 0},
        {1, 0, 1, 0},
        {1, 1, 0, 0},
        {1, 1, 1, 0},
    }
    V := len(graph)

    if hasUniversalSink(graph, V) {
        fmt.Println("存在通用汇点")
    } else {
        fmt.Println("不存在通用汇点")
    }
}

注意：

  • 在检查入度时，我们跳过了i == j的情况，因为自环通常不计入入度。
  • 这个算法的时间复杂度是O(V2)O(V^2)，因为它需要遍历矩阵的每一行和列来检查出度和入度。但是，由于题目询问的是是否存在一个可以在O(V)O(V)时间完成的算法，实际上对于这个问题，由于需要全面检查每个结点的入度和出度，O(V)O(V)时间复杂度的算法在常规意义下是不存在的（除非图具有特殊性质或额外信息，如稀疏性、边的有序性等，但这些在问题描述中未提及）。

如果图非常稀疏，或者你知道一些额外的信息（如边的有序列表等），那么可能可以通过优化来减少不必要的检查，但这通常仍然需要至少O(V+E)O(V + E)的时间复杂度，其中EE是边的数量。在本问题中，由于我们必须检查每个结点的所有入边和出边，所以O(V2)O(V^2)是不可避免的。

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

讯飞星火：

package main

import "fmt"

func findUniversalSink(adjMatrix [][]int) int {
    n := len(adjMatrix)
    inDegree := make([]int, n)
    outDegree := make([]int, n)

    // 计算每个节点的入度和出度
    for i := 0; i < n; i++ {
        for j := 0; j < n; j++ {
            if adjMatrix[i][j] == 1 {
                outDegree[i]++
                inDegree[j]++
            }
        }
    }

    // 检查是否存在通用汇点
    for i := 0; i < n; i++ {
        if inDegree[i] == n-1 && outDegree[i] == 0 {
            return i
        }
    }

    return -1 // 如果没有找到通用汇点，返回-1
}

func main() {
    adjMatrix := [][]int{
        {0, 1, 0, 0},
        {0, 0, 1, 0},
        {0, 0, 0, 1},
        {0, 0, 0, 0},
    }

    universalSink := findUniversalSink(adjMatrix)
    if universalSink != -1 {
        fmt.Printf("Universal sink found at node %d
", universalSink)
    } else {
        fmt.Println("No universal sink found")
    }
}

360智脑：

在有向图中，通用汇点（Universal Sink）是一个特殊的节点，它指向所有其他节点，但没有其他节点指向它。我们可以通过检查邻接矩阵来确定是否存在这样的节点。以下是一个使用Go语言编写的算法，用于在邻接矩阵表示的有向图中查找通用汇点：

func findUniversalSink(adjMatrix [][]int, V int) (bool, int) {
    i := 0
    j := 0

    // 遍历邻接矩阵
    for i < V && j < V {
        if adjMatrix[i][j] == 1 {
            // 如果当前位置是1，说明第i个节点指向第j个节点，所以i不可能是通用汇点
            // 因此，我们移动到下一行，继续检查
            i++
        } else {
            // 如果当前位置是0，说明第i个节点不指向第j个节点，所以j可能是通用汇点
            // 因此，我们移动到下一列，继续检查
            j++
        }
    }

    // 现在i要么越界，要么是通用汇点的索引
    // 我们需要验证i是否真的是通用汇点
    if i == V {
        return false, -1 // 没有找到通用汇点
    }

    // 检查第i个节点是否有出边
    for k := 0; k < V; k++ {
        if adjMatrix[i][k] == 1 {
            return false, -1 // 第i个节点有出边，不是通用汇点
        }
    }

    // 检查第i个节点的入度是否为V-1
    inDegree := 0
    for k := 0; k < V; k++ {
        if adjMatrix[k][i] == 1 {
            inDegree++
        }
    }

    if inDegree == V-1 {
        return true, i // 找到了通用汇点
    }

    return false, -1 // 没有找到通用汇点
}

// 示例用法
func main() {
    // 假设有一个5个节点的图，其邻接矩阵如下
    adjMatrix := [][]int{
        {0, 1, 0, 0, 1},
        {0, 0, 1, 0, 1},
        {0, 0, 0, 1, 1},
        {0, 0, 0, 0, 1},
        {0, 0, 0, 0, 0},
    }
    V := 5 // 节点数

    exists, index := findUniversalSink(adjMatrix, V)
    if exists {
        fmt.Printf("存在通用汇点，索引为: %d\n", index)
    } else {
        fmt.Println("不存在通用汇点")
    }
}

这个算法首先尝试找到一个可能的通用汇点，然后验证它是否满足通用汇点的条件。算法的时间复杂度是O(V)，因为我们最多遍历一次邻接矩阵的每一行和每一列。

智谱清言：

为了判断一个有向图是否存在一个通用汇点，我们可以遍历所有的节点，检查每个节点是否满足条件：它的入度为|V|-1且出度为0。以下是使用Go语言实现的算法：

package main
import (
	"fmt"
)
// Graph represents a directed graph with a given number of vertices.
type Graph struct {
	V int
	A [][]int
}
// NewGraph creates a new directed graph with V vertices and no edges.
func NewGraph(V int) *Graph {
	return &Graph{
		V: V,
		A: make([][]int, V),
	}
}
// AddEdge adds a directed edge from vertex 'from' to vertex 'to' in the graph.
func (g *Graph) AddEdge(from, to int) {
	g.A[from] = append(g.A[from], to)
}
// ExistsUniversalSink checks if there exists a universal sink in the graph.
func (g *Graph) ExistsUniversalSink() bool {
	// Initialize the inDegree count for all vertices.
	inDegree := make([]int, g.V)
	for i := 0; i < g.V; i++ {
		inDegree[i] = 0
	}
	// Calculate inDegree for all vertices.
	for _, row := range g.A {
		for _, to := range row {
			inDegree[to]++
		}
	}
	// Find a vertex with inDegree = V-1 and outDegree = 0.
	for i := 0; i < g.V; i++ {
		if inDegree[i] == g.V-1 && len(g.A[i]) == 0 {
			return true
		}
	}
	return false
}
func main() {
	// Create a graph with 4 vertices.
	graph := NewGraph(4)
	// Add edges to the graph.
	graph.AddEdge(0, 1)
	graph.AddEdge(0, 2)
	graph.AddEdge(1, 2)
	graph.AddEdge(1, 3)
	graph.AddEdge(2, 3)
	// Check if the graph has a universal sink.
	if graph.ExistsUniversalSink() {
		fmt.Println("The graph has a universal sink.")
	} else {
		fmt.Println("The graph does not have a universal sink.")
	}
}

这段代码首先定义了一个Graph类型，用来表示有向图。NewGraph函数用来创建一个指定顶点数的图，初始时不含任何边。AddEdge函数用来向图中添加有向边。ExistsUniversalSink函数检查图中是否存在一个通用汇点。它通过计算每个节点的入度来完成，然后寻找入度为顶点总数减一且出度为零的节点。

在main函数中，我们创建了一个有4个顶点的图，并添加了若干边，然后调用ExistsUniversalSink函数来判断图中是否存在通用汇点，并输出结果。

这个算法的时间复杂度是O(V)，因为我们只需要遍历一次所有的顶点和边来计算入度，不需要考虑每个顶点的出度，因为对于每个顶点，出度为零是在入度计算之后自然得到的。

天工：

要判断一个有向图是否存在通用汇点，我们可以利用邻接矩阵的一个特性：如果存在一个通用汇点，那么该点的行上的元素除了对角线元素外都应该是0（因为出度为0），而列上的元素除了对角线元素外都应该不是0（因为入度为|V|-1）。

以下是一个Go语言实现的算法，它可以在O(V)时间内完成判断：

func findUniversalSink(adjMatrix [][]int) int {
    V := len(adjMatrix)
    rowIndex := 0
    colIndex := 0

    // 我们只需要遍历邻接矩阵的一行或一列就可以找到通用汇点
    for rowIndex < V && colIndex < V {
        if adjMatrix[rowIndex][colIndex] == 1 {
            // 如果当前位置是1，说明rowIndex行对应的节点不是通用汇点，因为它的出度不为0
            // 所以我们移动到下一行
            rowIndex++
        } else {
            // 如果当前位置是0，说明colIndex列对应的节点可能是通用汇点，因为它的入度可能为|V|-1
            // 所以我们移动到下一列
            colIndex++
        }
    }

    // 检查找到的列是否满足通用汇点的条件
    if isUniversalSink(adjMatrix, colIndex) {
        return colIndex
    }

    // 如果不满足条件，则不存在通用汇点
    return -1
}

func isUniversalSink(adjMatrix [][]int, colIndex int) bool {
    V := len(adjMatrix)

    // 检查该列的入度是否为|V|-1
    inDegree := 0
    for _, row := range adjMatrix {
        if row[colIndex] == 1 {
            inDegree++
        }
    }

    // 检查该行的出度是否为0
    outDegree := 0
    for _, val := range adjMatrix[colIndex] {
        if val == 1 {
            outDegree++
        }
    }

    // 通用汇点的入度应为|V|-1，出度应为0
    return inDegree == V-1 && outDegree == 0
}

这个算法首先通过遍历一行或一列来确定一个候选的通用汇点，然后通过isUniversalSink函数检查该候选点是否满足通用汇点的条件。如果满足，返回该点的索引；如果不满足，返回-1表示不存在通用汇点。整个过程只需要遍历一次邻接矩阵的一行或一列，因此时间复杂度为O(V)。

chatgpt：

下面是用Go语言实现判断有向图是否存在通用汇点的算法：

package main

import "fmt"

func findUniversalSink(adjMatrix [][]int) int {
	n := len(adjMatrix)
	row, col := 0, 0

	for row < n && col < n {
		if adjMatrix[row][col] == 1 {
			col++
		} else {
			row++
		}
	}

	if row == n {
		return -1 // 没有通用汇点
	}

	for i := 0; i < n; i++ {
		if i != row && (adjMatrix[row][i] == 1 || adjMatrix[i][row] != 1) {
			return -1 // 不是通用汇点
		}
	}

	return row // 返回通用汇点的索引
}

func main() {
	graph := [][]int{
        {0, 0, 1, 1},
        {0, 0, 1, 1},
        {0, 0, 0, 0},
        {0, 0, 1, 0},
    }
    
    result := findUniversalSink(graph)
    if result == -1 {
        fmt.Println("图中不存在通用汇点")
    } else {
        fmt.Printf("图中的通用汇点为结点 %d\n", result)
    }
}

该算法首先遍历邻接矩阵，找到第一个可能的通用汇点。然后检查该节点是否满足入度为∣V∣−1|V|-1且出度为0的条件。如果满足，则返回该节点的索引；否则，表示不存在通用汇点，返回-1。

请注意，这里假设输入的邻接矩阵是一个方阵，并且图中最多只有一个通用汇点。如果你的输入不符合这些条件，请对代码进行相应的调整。

kimi：

在有向图中，一个通用汇点（universal sink）是一个特殊的节点，它具有以下两个特征：

  1. 它的入度是图中所有节点数量减一，即它从图中的每个其他节点都有一个直接的入边。
  2. 它的出度是0，即它不向图中的任何其他节点发出边。

要判断一个有向图是否存在通用汇点，我们可以遵循以下步骤：

  1. 遍历邻接矩阵的每一行，寻找一个行的和为V-1的节点，这表示此节点的入度为V-1。
  2. 同时，检查这个节点的列是否全为0，以确保它的出度为0。

这个算法的时间复杂度为O(V)，因为我们需要遍历邻接矩阵的V行。

以下是使用Go语言实现的代码示例：

package main

import "fmt"

func hasUniversalSink(adjMatrix [][]int, V int) bool {
    for i := 0; i < V; i++ {
        // 检查第i行的和是否为V-1
        if sumRow(adjMatrix, i) == V-1 {
            // 检查第i列是否全为0
            if allZerosInColumn(adjMatrix, i) {
                return true
            }
        }
    }
    return false
}

// sumRow 计算邻接矩阵中指定行的元素和
func sumRow(adjMatrix [][]int, row int) int {
    sum := 0
    for _, val := range adjMatrix[row] {
        sum += val
    }
    return sum
}

// allZerosInColumn 检查邻接矩阵中指定列的所有元素是否全为0
func allZerosInColumn(adjMatrix [][]int, col int) bool {
    for _, row := range adjMatrix {
        if row[col] != 0 {
            return false
        }
    }
    return true
}

func main() {
    // 示例邻接矩阵
    adjMatrix := [][]int{
        {0, 1, 0, 0},
        {0, 0, 1, 0},
        {0, 0, 0, 1},
        {1, 1, 1, 0},
    }
    V := 4 // 节点的数量

    if hasUniversalSink(adjMatrix, V) {
        fmt.Println("存在通用汇点")
    } else {
        fmt.Println("不存在通用汇点")
    }
}

这段代码定义了hasUniversalSink函数，它接受邻接矩阵和节点数量V作为参数，并返回一个布尔值，表示是否存在通用汇点。sumRow和allZerosInColumn是辅助函数，分别用于计算行的和和检查列是否全为0。在main函数中，我们给出了一个示例邻接矩阵，并调用hasUniversalSink函数来检查是否存在通用汇点。

混元：

要判断有向图GG是否存在一个通用汇点，我们可以遍历邻接矩阵，统计每个节点的入度和出度。在遍历过程中，我们可以同时更新入度和出度，并检查当前节点是否满足通用汇点的条件。以下是使用Go语言实现的算法：

package main

import "fmt"

func hasUniversalSink(adjMatrix [][]int) bool {
    n := len(adjMatrix) // 获取节点数
    inDegree := make([]int, n) // 存储每个节点的入度
    outDegree := make([]int, n) // 存储每个节点的出度

    for i := 0; i < n; i++ {
        for j := 0; j < n; j++ {
            if adjMatrix[i][j] == 1 {
                outDegree[i]++ // 更新节点i的出度
                inDegree[j]++ // 更新节点j的入度
            }
        }
    }

    for i := 0; i < n; i++ {
        if inDegree[i] == n-1 && outDegree[i] == 0 {
            return true // 找到通用汇点，返回true
        }
    }

    return false // 未找到通用汇点，返回false
}

func main() {
    adjMatrix := [][]int{
        {0, 1, 0, 0},
        {0, 0, 1, 0},
        {0, 0, 0, 1},
        {1, 0, 0, 0},
    }

    fmt.Println(hasUniversalSink(adjMatrix)) // 输出: true
}

这个算法的时间复杂度为O(V2)O(V^2)，因为在最坏情况下，我们需要遍历整个邻接矩阵。然而，对于有向图来说，这个算法已经是O(V)O(V)时间复杂度了，因为在有向图中，最多只有∣V∣×∣V∣|V| \times |V|条边，所以遍历整个邻接矩阵的时间复杂度为O(∣V∣2)O(|V|^2)，但由于我们只关心单个节点的入度和出度，实际上在遍历过程中每个节点和每条边都只会被访问一次，因此可以认为是O(V)O(V)的。这里需要注意的是，原始答案中的描述可能有误，因为对于有向图的邻接矩阵，判断通用汇点的算法不可能达到O(V)O(V)的时间复杂度，除非图中边的数量远小于V2V^2。

【版权声明】本文为华为云社区用户原创内容，转载时必须标注文章的来源（华为云社区）、文章链接、文章作者等基本信息， 否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱： cloudbbs@huaweicloud.com
  • 点赞
  • 收藏
  • 关注作者

评论（0）

0/1000
抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认 取消

加入云驻计划，成为创作者

  • 华为云周边好礼
  • 免费体验产品
  • 特殊身份标识
  • 线下官方门票
  • 内部专家零距离
  • 与10000+优质创作者共同成长
立即加入