算法-全排列(含参考实现代码)
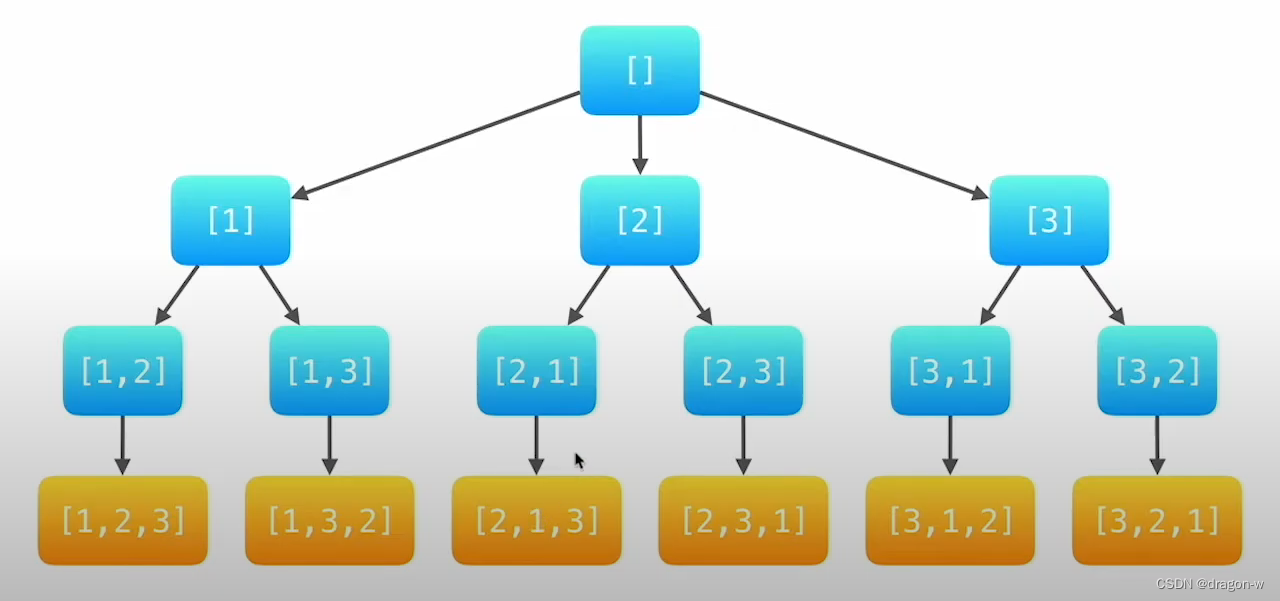
【摘要】 定义从n个不同元素中任取m(m≤n)个元素,按照一定的顺序排列起来,叫做从n个不同元素中取出m个元素的一个排列。当m=n时所有的排列情况叫全排列。公式:全排列数f(n)=n!(定义0!=1)---百度百科解题思路按顺序枚举每一个位置可能出现的字符。之前已经出现的字符在接下来要选择的字符中不能出现。编辑 从图上可以看出,我们获得所以排列的结果,既可以使用广度优先遍历,也可以使用深度优先遍...
定义
从n个不同元素中任取m(m≤n)个元素,按照一定的顺序排列起来,叫做从n个不同元素中取出m个元素的一个排列。当m=n时所有的排列情况叫全排列。
公式:全排列数f(n)=n!(定义0!=1)
---百度百科
解题思路
- 按顺序枚举每一个位置可能出现的字符。
- 之前已经出现的字符在接下来要选择的字符中不能出现。
从图上可以看出,我们获得所以排列的结果,既可以使用广度优先遍历,也可以使用深度优先遍历,先看广度优先遍历的实现。
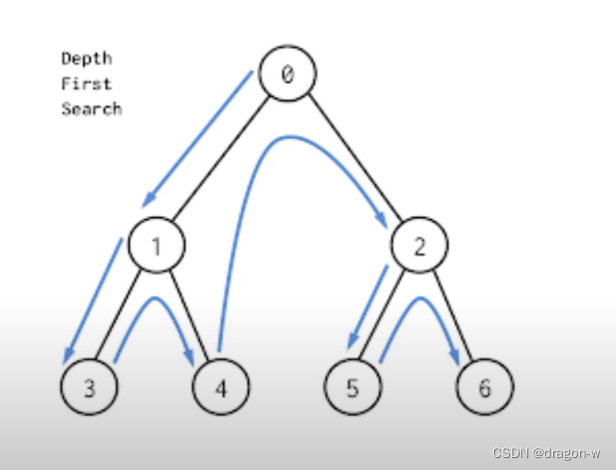
广度优先遍历实现全排列
广度优先遍历是按照距离根节点的距离来访问的。
广度优先遍历是按“层”的概念进行遍历的。
- 从某一个顶点v出发,在访问了v之后依次访问v的各个没有访问到的邻接点
- 然后分别从这些邻接点出发,依次访问他们的临界点
深度优先遍历实现全排列
- 状态:每一个节点表示了求解问题的不同阶段。
- 深度优先遍历在回到上一层节点时需要“状态重置”。
- 递归到第几层,我们使用变量depth来记录,当遍历到的层数和输入的数组个数相等时候,递归终止。
- 已经选择了哪些字符,我们命名为path,代表从根节点到某个中间节点或者叶子节点的路径。
- 使用布尔数组used,表示当前考虑的字符是否在之前已经选择过,也就是当前考虑的字符是否在path变量里,这样我们可以以O(1)的时间复杂度完成判断。
树形问题上的深度优先遍历也就是大名鼎鼎的回溯算法,上面提到的“状态重置”就是“回溯算法”里回溯的意思。
深度优先遍历的过程,就是不断的在列表的末尾添加或删除元素的过程,相当于一个栈。
深度优先遍历的过程描述二:从根节点出发,一头扎到底,然后再返回一层,再扎到底,直到全部节点都走完。
下面是示例代码:
执行后的输出效果:
【声明】本内容来自华为云开发者社区博主,不代表华为云及华为云开发者社区的观点和立场。转载时必须标注文章的来源(华为云社区)、文章链接、文章作者等基本信息,否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者



评论(0)