🏆 作者简介，愚公搬代码
🏆《头衔》：华为云特约编辑，华为云云享专家，华为开发者专家，华为产品云测专家，CSDN博客专家，CSDN商业化专家，阿里云专家博主，阿里云签约作者，腾讯云优秀博主，腾讯云内容共创官，掘金优秀博主，亚马逊技领云博主，51CTO博客专家等。
🏆《近期荣誉》：2022年度博客之星TOP2，2023年度博客之星TOP2，2022年华为云十佳博主，2023年华为云十佳博主等。
🏆《博客内容》：.NET、Java、Python、Go、Node、前端、IOS、Android、鸿蒙、Linux、物联网、网络安全、大数据、人工智能、U3D游戏、小程序等相关领域知识。
🏆🎉欢迎 👍点赞✍评论⭐收藏

🚀前言

计算机中的校验码（Check Code 或 Error-Detecting Code）是用于检测数据在存储或传输过程中是否发生错误的一种机制。校验码通过在数据中添加额外的信息来实现，这些信息可以在数据接收端被用来检查数据是否完整、正确。校验码的使用非常广泛，包括内存校验、网络通信、数据存储等多个领域。

🚀一、校验码

🔎1.奇偶校验

🦋1.1 概念

奇偶校验是计算机通信和数据存储中常用的一种简单校验码方法，用于检测数据在传输或存储过程中是否发生了错误。奇偶校验通过添加一个额外的位，即奇偶校验位，来确保数据位（包括校验位自身）中“1”的总数是奇数（奇校验）或偶数（偶校验）。这种方法可以检测出任意奇数位的错误，但不能检测出偶数位的错误，也无法定位错误发生的具体位置。

工作原理

• 偶校验：在偶校验中，数据加上校验位后，"1"的总数应该是偶数。如果数据中"1"的数量已经是偶数，校验位就设为0；如果"1"的数量是奇数，则校验位设为1，以确保包含校验位的总数据中"1"的数量为偶数。

• 奇校验：在奇校验中，数据加上校验位后，"1"的总数应该是奇数。如果数据中"1"的数量已经是奇数，校验位就设为0；如果"1"的数量是偶数，则校验位设为1，以确保包含校验位的总数据中"1"的数量为奇数。

例子

假设我们要传输数据1011，我们使用奇校验和偶校验来计算校验位：

• 使用偶校验：

  • 数据1011中有三个"1"，是奇数。
  • 为了使总数成为偶数，我们添加校验位1。
  • 因此，带校验位的数据变为10111。

• 使用奇校验：

  • 数据1011中有三个"1"，已经是奇数。
  • 为了保持总数为奇数，我们添加校验位0。
  • 因此，带校验位的数据变为10110。

优缺点

• 优点：

  • 实现简单，易于理解。
  • 能够检测任何单个位的错误。

• 缺点：

  • 无法检测偶数位的错误（例如，如果同时有两位发生变化）。
  • 无法确定错误发生的位置，也就是说，它不能纠错。

奇偶校验广泛用于早期的计算机系统和一些现代的低级通信协议中，尽管它的错误检测能力有限，但由于其实现的简单性，仍然在特定场景下有其应用价值。

🦋1.2 练习

1、给出编码1001101的奇校验码和偶校验码（ ）。

A 10011011, 10011010
B 10011011, 10011011
C 10011010, 10011010
D 10011010, 10011010

解析：

为了给出编码1001101的奇校验码和偶校验码，我们首先需要计算原始编码中"1"的数量。

原始编码：1001101

• "1"的数量为4，是偶数。

奇校验码

• 由于奇校验要求包含校验位在内的"1"的总数为奇数，而原始编码中"1"的数量已经是偶数，因此我们需要添加一个"1"作为校验位，以使得总数变为奇数。
• 结果为：10011011

偶校验码

• 由于偶校验要求包含校验位在内的"1"的总数为偶数，而原始编码中"1"的数量已经是偶数，因此我们需要添加一个"0"作为校验位，以保持总数仍然是偶数。
• 结果为：10011010

因此，给出编码1001101的奇校验码是10011011，偶校验码是10011010。

选项A正确：10011011（奇校验码），10011010（偶校验码）。

🔎2.模 2 除法

模2除法是一种在计算机科学中用于生成循环冗余校验（CRC）码的算术运算方法。它与传统的长除法运算类似，但在模2除法中，不执行进位和借位操作。这种方法广泛应用于通信和存储系统中，用于检测数据传输或存储过程中的错误。

模2除法的操作规则：

1. 加法和减法：模2加法等同于二进制加法而不考虑进位，相当于逻辑异或（XOR）操作。也就是说，同位值相同则结果为0，不同则结果为1。
2. 乘法：模2乘法与普通的二进制乘法相同。
3. 除法：模2除法类似于普通的长除法，但没有借位。除法操作中的减法被替换为模2加法（即异或操作）。

使用模2除法生成CRC的过程：

1. 选择一个预定的生成多项式：生成多项式定义了CRC的特性，常用的生成多项式包括CRC-16、CRC-CCITT、CRC-32等。
2. 将数据准备进行除法操作：通常通过将原始数据后附加足够长度的0（长度通常与生成多项式的位数一致）来准备数据。
3. 执行模2除法：使用生成多项式作为除数，对准备好的数据进行模2除法运算。与传统的长除法类似，不过每一步的减法被替换为异或操作。
4. 取余数作为CRC：模2除法的余数即为CRC码，该余数被附加到原始数据的末尾，形成一个新的、更长的数据块。这个新数据块通过同样的生成多项式进行模2除法时，如果没有错误，最终的余数应为0（或特定的非零值，取决于CRC算法的具体设计）。

🦋2.1 加法

模2加法是指对于两个二进制数的对应位进行相加，结果取模2。也就是说，如果两位都是0或者都是1，结果就是0，如果两位一个是0一个是1，结果就是1。

0＋0＝0   0＋1＝1  1＋0＝1   1＋1＝0

例如：0101 + 0011 = 0110，列竖式计算：

	0 1 0 1
+	0 0 1 1
—————————————	
	0 1 1 0

🦋2.2 减法

模2减法是指在模2的情况下进行减法运算。在模2的情况下，只有两个可能的值：0和1。因此，模2减法的规则如下：

0－0＝0   0－1＝1   1－0＝1   1－1＝0

例如：0110－0011＝0101，列竖式计算：

    0 1 1 0
 -  0 0 1 1
—————————————	
    0 1 0 1

🦋2.3 乘法

模2乘法指的是将两个数相乘后取模2的结果。换句话说，模2乘法就是判断两个数的乘积是奇数还是偶数。

在模2乘法中，如果两个数中有一个数是偶数，那么乘积一定是偶数；如果两个数都是奇数，那么乘积是奇数。

0×0＝0   0×1＝0   1×0＝0   1×1＝1

多位二进制模2乘法类似于普通意义上的多位二进制乘法
不同之处在于后者累加中间结果（或称部分积）时采用带进位的加法
模2乘法对中间结果的处理方式采用的是模2加法
例如1011 × 101＝100111，列竖式计算：

      	1 0 1 1
×  	 	  1 0 1
———————————————————			
        1 0 1 1
      0 0 0 0
+   1 0 1 1
———————————————————		
    1 0 0 1 1 1
————————————————

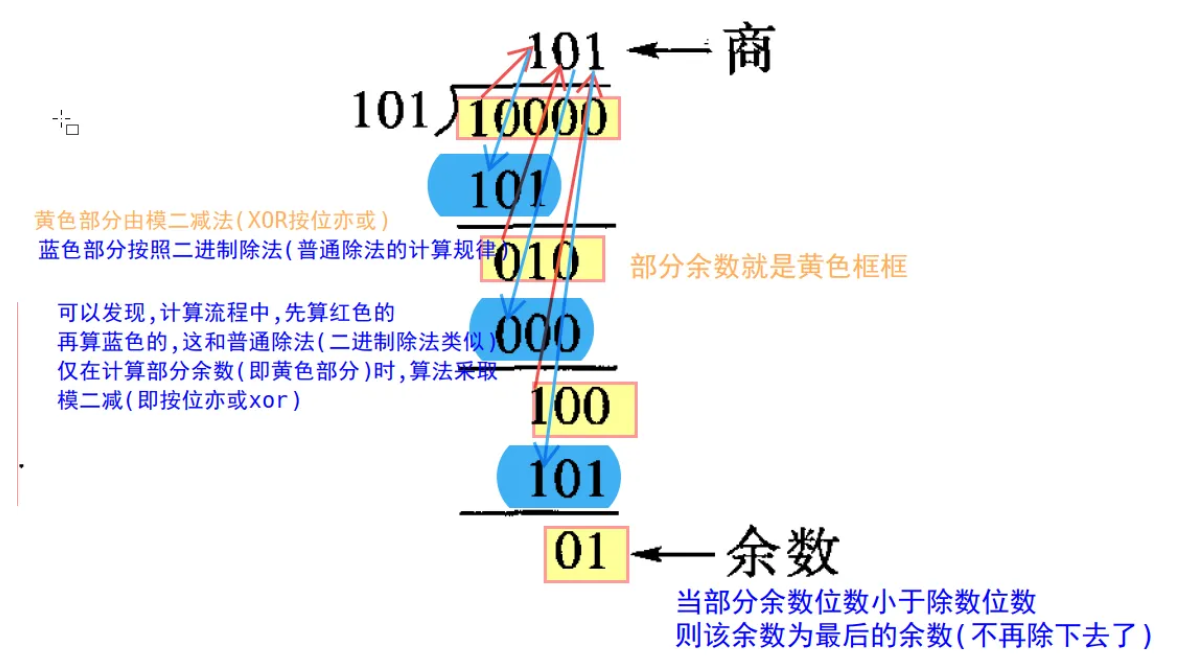
🦋2.4 除法

模2除法是模2乘法的逆运算。模2除法具有下列三个性质：

1、当最后余数的位数小于除数位数时，除法停止。

2、当被除数的位数小于除数位数时，则商数为0，被除数就是余数。

3、只要被除数或部分余数的位数与除数一样多，且最高位为1，不管其他位是什么数，皆可商1。

🔎3.循环冗余校验CRC

🦋3.1 概念

循环冗余校验（CRC）是一种常见的检测数据传输或存储过程中错误的方法，广泛用于通信系统、网络协议和数据存储验证。CRC通过对数据块应用模2除法，并使用特定的生成多项式来生成一个短的、固定长度的校验码（即CRC码），随数据一起发送或存储。接收方或读取方再次计算数据的CRC码，并与传送或存储的CRC码进行比较，以此来检测数据是否完整、无误。

CRC的工作原理

1. 选择生成多项式：CRC算法首先定义一个生成多项式，这个多项式通常表示为G(x)。生成多项式是CRC算法的核心，不同的应用可能选择不同的生成多项式。

2. 准备数据：在数据的尾部附加足够的零。这个长度通常等于生成多项式的阶数。例如，如果生成多项式是8位长（例如CRC-8），则在数据的末尾添加7个零（因为阶数是位数减1）。

3. 应用模2除法：使用生成多项式对原始数据（附加了零的）执行模2除法。这里的“模2除法”意味着除法过程中所有的减法操作都被替换为异或（XOR）操作。

4. 得到CRC码：模2除法的余数就是CRC码。这个余数的长度与生成多项式的阶数相同。

5. 发送或存储数据：原始数据（不包括之前附加的零）和它的CRC码一起被发送或存储。

6. 验证：接收方收到数据后，对整个数据（包括CRC码）使用相同的生成多项式再次执行模2除法。如果数据完整、无误，最终的余数应该是0（或者是特定的预定值，取决于CRC算法的具体实现）。

为什么CRC有效

CRC之所以能有效检测错误，是因为它基于多项式运算。这种方法能够检测到的错误类型包括：

• 单位错误
• 偶数位错误（取决于CRC的长度和选用的多项式）
• 小段数据错误（burst error）
• 数据位反转错误

常见的生成多项式

• CRC-32：用于以太网和许多其他形式的网络通信，生成多项式是0x04C11DB7。
• CRC-16-CCITT：广泛用于通信协议，特别是在PPP协议中，生成多项式是0x1021。

注意点

尽管CRC非常有效地检测了大部分错误，但它不是绝对完美的。理论上存在极少数情况，错误数据的CRC码可能与原始数据的CRC码相同，导致错误无法被检测到。然而，在实际应用中，这种概率非常小，因此CRC仍然是一种非常可靠的错误检测方法。

🦋3.2 练习

1、待发送的信息为101001，生成多项式为G（x）=x^3 + x^2 + 1，计算编码后的信息。

解析：

为了计算给定信息101001使用生成多项式G(x) = x^3 + x^2 + 1编码后的信息，我们将遵循CRC的生成过程。这个过程包括将信息表示为多项式、附加额外的零以匹配生成多项式的阶数、执行模2除法，最后将得到的余数（CRC码）附加到原始信息上。

步骤1: 表示信息和生成多项式

• 信息多项式：101001 可表示为 x^5 + x^3 + 1。
• 生成多项式 G(x) = x^3 + x^2 + 1，表示为1101。

步骤2: 附加额外的零
生成多项式G(x)是3阶的，所以我们需要在信息末尾附加3个零，准备进行模2除法。原始信息101001变为101001000。

步骤3: 执行模2除法
使用1101（生成多项式）对101001000执行模2除法，得到余数。这一步类似于长除法，但是减法被替换为异或操作（模2加法）。

过程如下：

   101001000
   --------
1101 | 101001000
       1101
       ----
        1110
        1101
        ----
          1110
          1101
          ----
            1100
            1101
            ----
             001

最终余数为001。

步骤4: 附加余数到原始信息
将得到的余数（001）附加到原始信息（不包含一开始附加的零）101001上，得到最终的编码后信息为101001001。

2、接收到的信息为101101001，生成多项式为G（x）=x^3 + x^2 + 1，判断传输是否有误码。

解析：

为了判断接收到的信息101101001是否有误码，我们可以使用生成多项式G(x) = x^3 + x^2 + 1进行校验。这个过程涉及将接收到的信息作为被除数，生成多项式作为除数执行模2除法。如果最终的余数为0，那么可以认为传输过程中没有误码；如果余数不为0，则表示传输过程中有误码。

步骤1: 表示信息和生成多项式

• 接收到的信息：101101001。
• 生成多项式 G(x) = x^3 + x^2 + 1，对应的二进制表示为1101。

步骤2: 执行模2除法
使用生成多项式1101对接收到的信息101101001进行模2除法。这里，不需要附加额外的零，因为我们是在校验阶段而不是在生成CRC码的阶段。

过程如下：

   101101001
   --------
1101 | 101101001
       1101
       ----
        1100
        1101
        ----
           1100
           1101
           ----
              11

因为不是0所以有误码

3、在（ ）校验方法中，采用模2运算来构造校验位。(2019上半年试题)

A.水平奇偶
B.垂直奇偶
C.海明码
D.循环冗余

解析：

A. 水平奇偶校验 和 B. 垂直奇偶校验：这两种奇偶校验方法通常用于简单的错误检测，特别是在通信或数据存储中。它们通过添加一个校验位来确保一组数据位中"1"的总数为奇数（奇校验）或偶数（偶校验）。虽然它们的实现可能涉及二进制运算，但并不特指使用模2运算来构造校验位。

C. 汉明码：汉明码是一种线性纠错码，能够不仅检测错误还能纠正错误，特别是单一位错误。它通过在数据位中插入多个校验位来实现，这些校验位是基于特定数据位的组合计算出来的，以确保每组位（包括数据位和校验位）中1的数量符合奇偶性要求。虽然汉明码的计算涉及二进制操作，但它的核心不是模2运算。

D. 循环冗余（CRC）：CRC是通过将数据视为一个大的多项式，并使用特定的生成多项式进行模2除法来生成校验位的方法。这种方法的核心正是模2运算，它在整个计算过程中使用异或操作来模拟除法和减法，最终生成的余数作为CRC校验码。CRC因其高效的错误检测能力而广泛应用于数据传输和存储系统中。

因此，正确答案是 D. 循环冗余。

🔎4.海明校验

🦋4.1 概念

汉明校验（Hamming Code）是一种错误检测和纠正的编码方法，由理查德·汉明（Richard Hamming）在20世纪50年代发明。汉明码不仅能发现单一位错误，还能自动纠正这类错误，使其在计算机内存、数据传输和其他需要高可靠性的系统中得到广泛应用。

工作原理

汉明码通过在数据位之间插入多个校验位（parity bits）来实现错误检测和纠正。校验位的位置通常是2的幂次方上（即第1、2、4、8位等），其值根据特定的数据位计算得出，以确保某个特定组合的位（包括数据位和校验位）中1的数量为偶数（偶校验）或奇数（奇校验），这取决于使用的是偶校验法还是奇校验法。

校验位的计算

1. 确定校验位数量：首先需要计算在给定数据长度下所需的校验位数量。如果数据长度为k位，需要添加r个校验位，那么必须满足条件：$(2^r \geq k + r + 1)$ 。

2. 计算校验位：每个校验位负责一组特定的位（包括数据位和校验位本身）。例如，第一个校验位（位1）负责所有位数为奇数的位；第二个校验位（位2）负责位数在2的倍数位置的位，等等。校验位的值被设置为使其所负责的位组中1的总数为偶数（或奇数）。

错误检测与纠正

接收端在收到数据后，重新计算每个校验位，并比较这些校验位与接收到的校验位。如果所有校验位都匹配，则假定没有错误发生。如果某些校验位不匹配，其不匹配的校验位的位置编号之和指示出了错误位的准确位置。这样，接收端可以直接翻转该位以纠正错误。

优缺点

• 优点：

  • 能够检测并纠正单一位的错误。
  • 实现简单，适用于错误率不高的场合。

• 缺点：

  • 随着数据位的增加，需要的校验位也会增加，这降低了数据传输的有效率。
  • 只能纠正单一位的错误和检测双位错误，对于多于两位的错误就无能为力。

汉明码因其能够自动纠正错误而被广泛应用于计算机内存、数据传输等领域，特别是在对数据完整性要求较高的系统中。尽管它不适用于错误率非常高的环境，但在许多应用场景中仍然是一种有效的错误控制方法。

🦋4.2 计算校验码位数

原始数据0110，n = 4

根据海明校验码公式可以得到需要添加的校验码位数k = 3

校验码放置的位置应为2的整数次幂，即Pi=2^i

于是我们得到了这样一个待计算的海明码：

其中，P0、P1、P2为三个我们添加的校验码

🦋4.3 确定校验组

接下来我们为每一个数据添加校验组，校验组是什么意思呢，就是这一下标对应的数据可以由一个校验组来唯一对应检验。通俗地讲，做法就是将每一个数据位的下标分解成校验码所在下标的和，（校验位不分解），拿我们的例子来看看：

🦋4.4 计算校验码的值得出海明校验码

计算海明校验码的最后一个步骤就是得出P0、P2、P3的具体值，其做法为：

计算Pi的值，就在校验组中将与Pi有关的那几组数据做 异或（相同为0，不同为1） 运算拿我们的例子来看看：

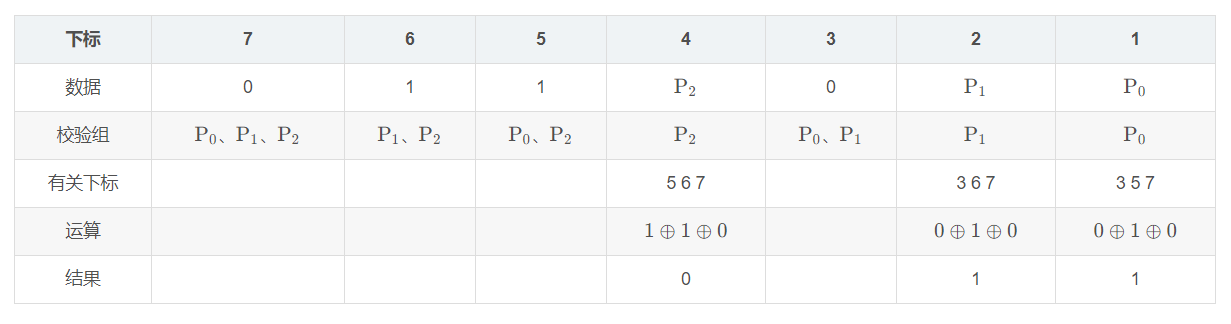
计算结束后，和原来的数据组合我们就得到了海明校验码：

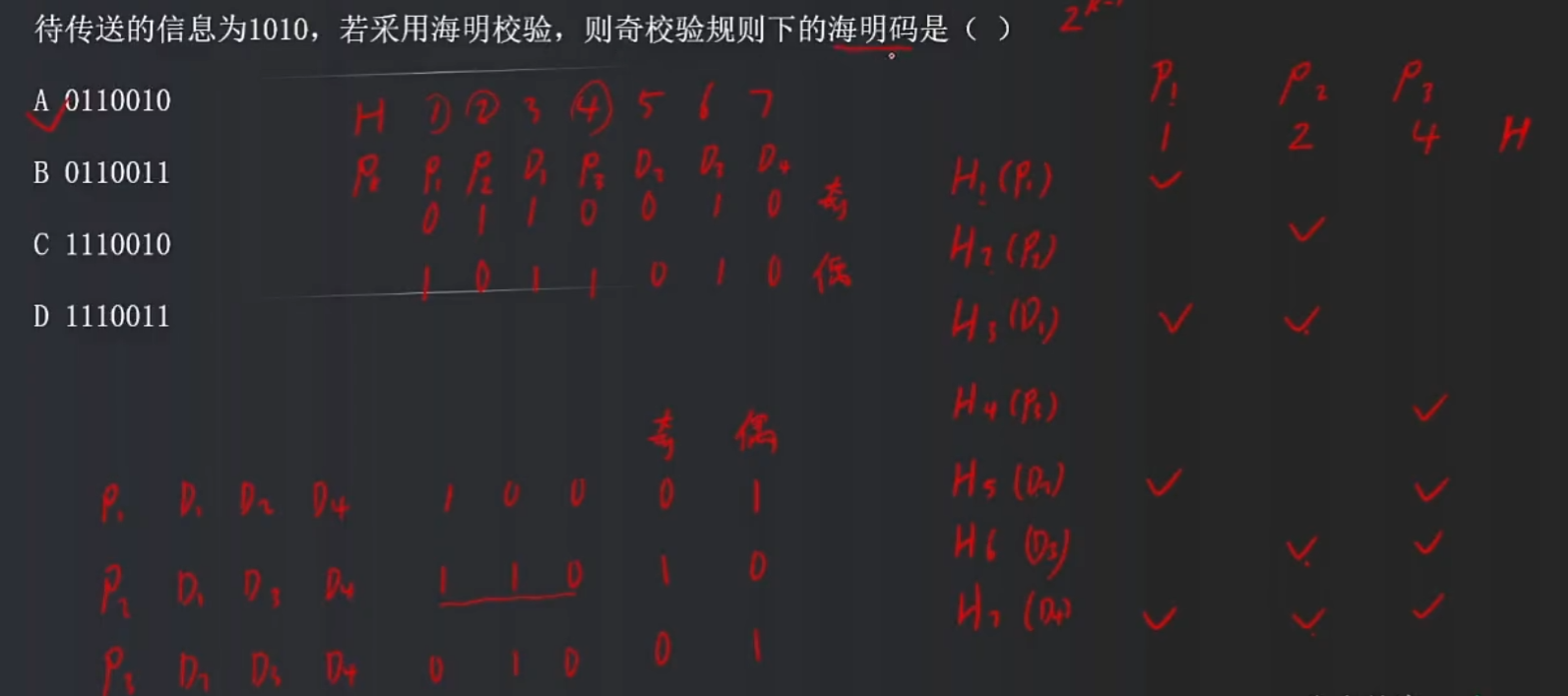
🦋4.5 练习

🚀感谢：给读者的一封信

亲爱的读者，

我在这篇文章中投入了大量的心血和时间，希望为您提供有价值的内容。这篇文章包含了深入的研究和个人经验，我相信这些信息对您非常有帮助。

如果您觉得这篇文章对您有所帮助，我诚恳地请求您考虑赞赏1元钱的支持。这个金额不会对您的财务状况造成负担，但它会对我继续创作高质量的内容产生积极的影响。

我之所以写这篇文章，是因为我热爱分享有用的知识和见解。您的支持将帮助我继续这个使命，也鼓励我花更多的时间和精力创作更多有价值的内容。

如果您愿意支持我的创作，请扫描下面二维码，您的支持将不胜感激。同时，如果您有任何反馈或建议，也欢迎与我分享。

再次感谢您的阅读和支持！

最诚挚的问候， “愚公搬代码”