💞💞 前言

hello hello~ ，这里是大耳朵土土垚~💖💖 ，欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹

💥个人主页：大耳朵土土垚的博客
💥 所属专栏：数据结构学习笔记 、排序算法合集
💥对于数据结构顺序表、链表、堆有疑问的都可以在上面数据结构的专栏进行学习哦~ 有问题可以写在评论区或者私信我哦~

一、选择排序

==基本思想==：

每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完 。

这里选择排序介绍两种——直接选择排序、堆排序

二、直接选择排序

✨✨在元素集合array[i]–array[n-1]中选择关键码最大(小)的数据元素
✨✨若它不是这组元素中的最后一个(第一个)元素，则将它与这组元素中的最后一个（第一个）元素交换
✨✨在剩余的array[i]–array[n-2]（array[i+1]–array[n-1]）集合中，重复上述步骤，直到集合剩余1个元素

直接选择排序类似于***将手上的无序的牌整理成有序***，我们常常是找出所有牌中最大的一个放在最前面，再从剩下的牌中找出最大的放在第二位…直到全部有序，这和直接选择排序的思想是一致的。
💥💥但是一次只选一个最大的消耗的时间比较长，所有我们每次挑出最大的同时把最小的也挑出来，如果是升序，就把最大的放在最后面，最小的放在最前面；如果是降序，则反过来。

直接选择排序代码实现：

// 直接选择排序
void SelectSort(int* a, int n)
{
	//找到首尾下标
	int begin = 0;
	int end = n - 1;
	//使用while多次循环来找到每趟最大最小的值
	while (begin < end)
	{
		int maxi = begin;
		int mini = begin;
		
		//一趟找最大最小的值
		for (int i = begin; i <= end; i++)
		{
			
			//找最小
			if (a[i] < a[mini])
			{
				mini = i;
			}
			//找最大
			if (a[i] > a[maxi])
			{
				maxi = i;
			}

		}

		//交换最大最小到最开始与最后的位置
		Swap(&a[mini], &a[begin]);
		//如果最开始begin位置就是最大，为防止被最小的交换我们则需要修正一下
		if (a[begin] == a[maxi])
		{
			maxi = mini;
		}
		Swap(&a[maxi], &a[end]);
		//交换完之后，begin++，end--，进行下一次选择
		begin++;
		end--;

	}
}

🥳🥳这里注意for循环是一趟遍历找到最大最小值，如果要全部排完序则需要while循环多次遍历；

🥳🥳此外找到最大最小值交换时还要注意交换的开始位置是不是最大值，如果是最大值我们就需要将最大值的下标maxi改成交换后的也就是maxi；当然如果不是最大值就无需交换；

结果如下：
以int a[] = {7,4,6,9,8,2,3,1}为例

Swap函数在这里🥳🥳：

//交换函数
void Swap(int* a,int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}

三、堆排序

堆排序在我们学习堆时就已经详细介绍过了，此外我们还利用堆排序解决了Topk问题
详情可以点击这里：数据结构——堆排序 、 堆排序应用——Topk问题
💓💓 在上面的堆排序中我们建立的是小堆，求的是降序；所以今天我们在这里将介绍堆排序——升序，我们需要利用大堆；
✨✨ 有小伙伴知道为什么我们要建大堆求升序，建小堆求降序吗？答案将在介绍完堆排序后面揭示🎉🎉大家可以先想一想🥳🥳

堆排序分为两个步骤：
1、建堆
2、排序

排序详细步骤如下：

1.升序建大堆，也就是所有的孩子节点都小于其父节点；
2. 然后将建成的大堆根节点（也就是所有节点中最大的节点）与最后一个节点交换，这样最大的节点就在最后了；
3. 然后将除去最后的最大节点剩下的节点看成一颗二叉树（此时这个二叉树除了根节点，其左右子树都是大堆）那么我们就可以利用堆向下调整法将根节点往下调整建成大堆；
4. 此时这个大堆的根节点就是剩余节点里面最大的，然后与剩下节点最后一个位置交换（也就是整个的倒数第二个节点）此时次大的数就在倒数第二个位置上；
5依次类推，循环34步骤直到升序完成。

图解如下：
以int a[] = {4,7,8,5,6,2,1,9}为例
1.建堆

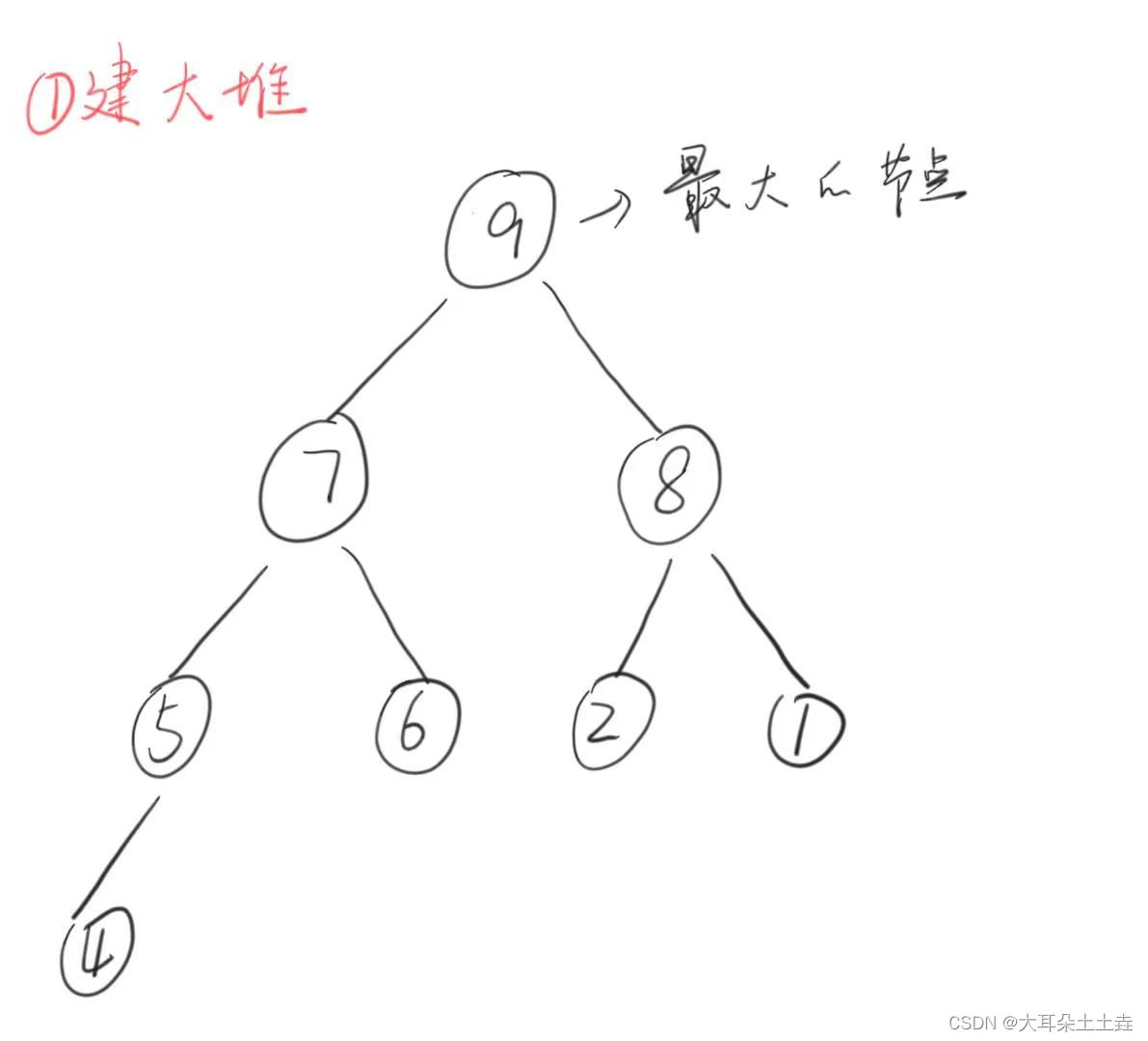
这里利用堆向下调整算法实现：

// 堆排序——建大堆
void AdjustDwon(int* a, int n, int root)
{
	//找到孩子节点
	int child = root * 2 + 1;
	
	//向下调整
	while (child < n)
	{
		//升序建大堆，找到最大的孩子节点
		if (child + 1 < n && a[child + 1] > a[child])
			child++;

		if (a[child] > a[root])
		{
			Swap(&a[child], &a[root]);
			root = child;
			child = root * 2 + 1;
		}
		else
			break;
		
	}
}

大家可以对比一下之前讲的堆排序建小堆有什么不同哦~

2.排序

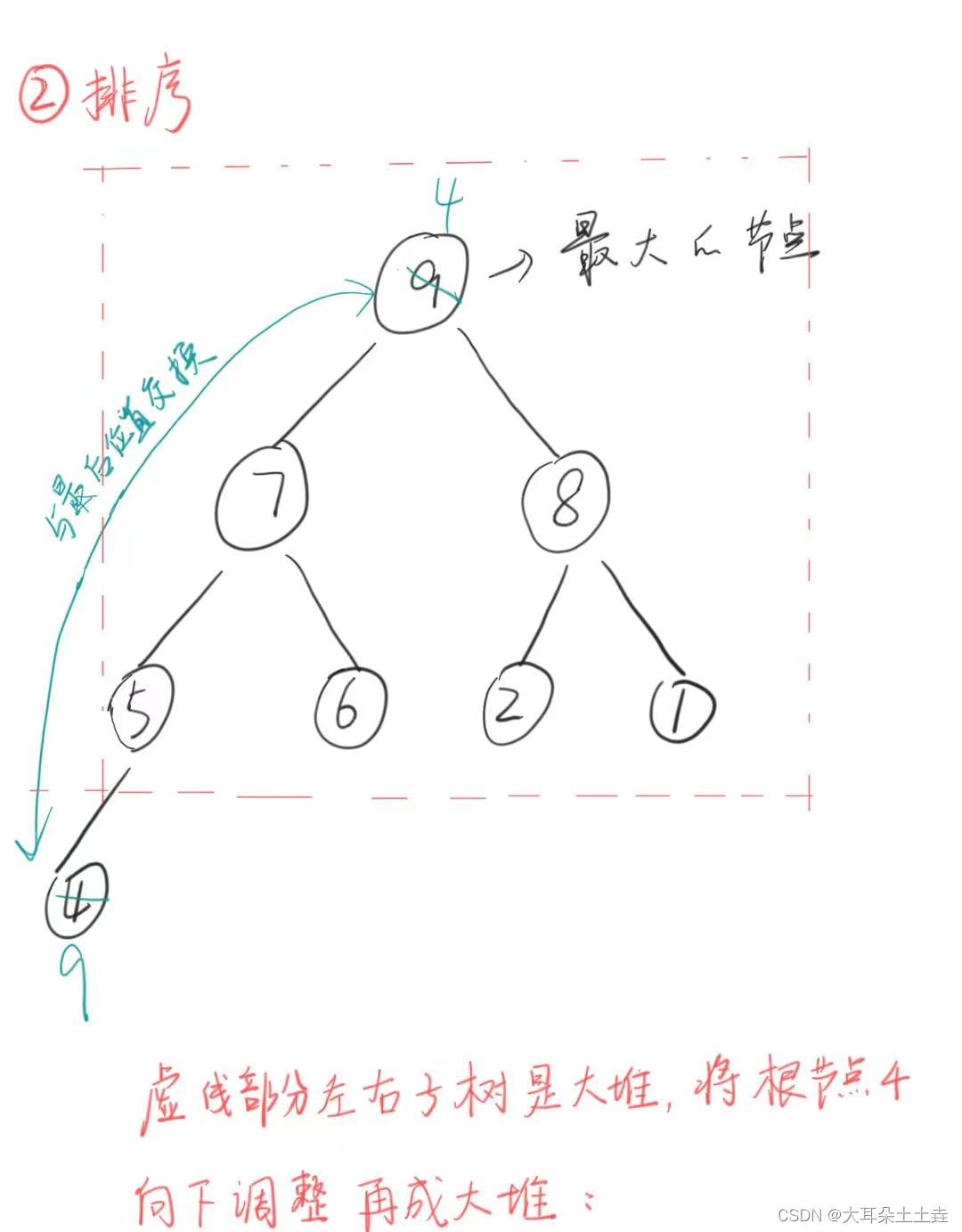
交换后将红色虚线剩余部分利用向下调整法建成大堆找出次大的数

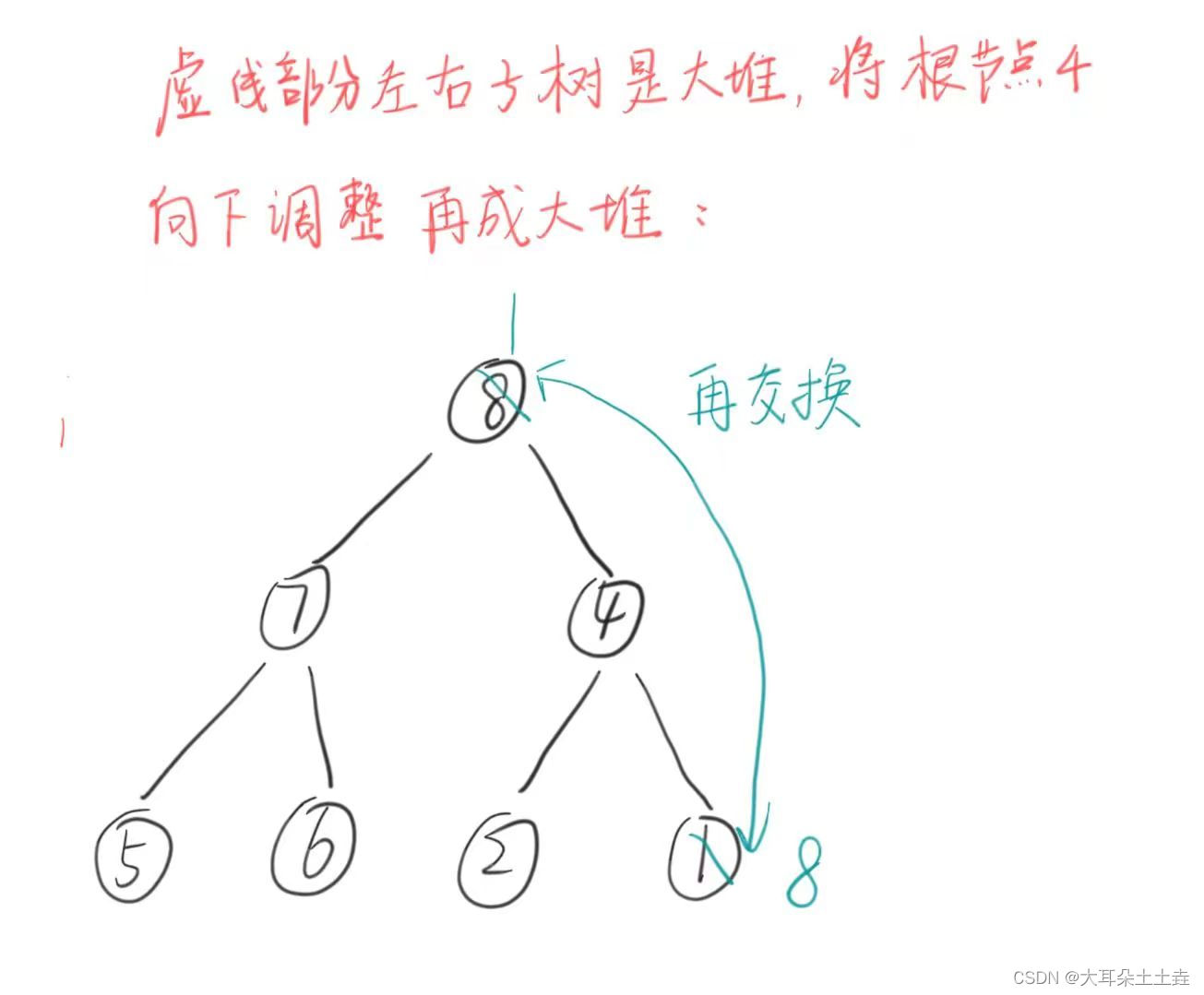
再与最后的数交换

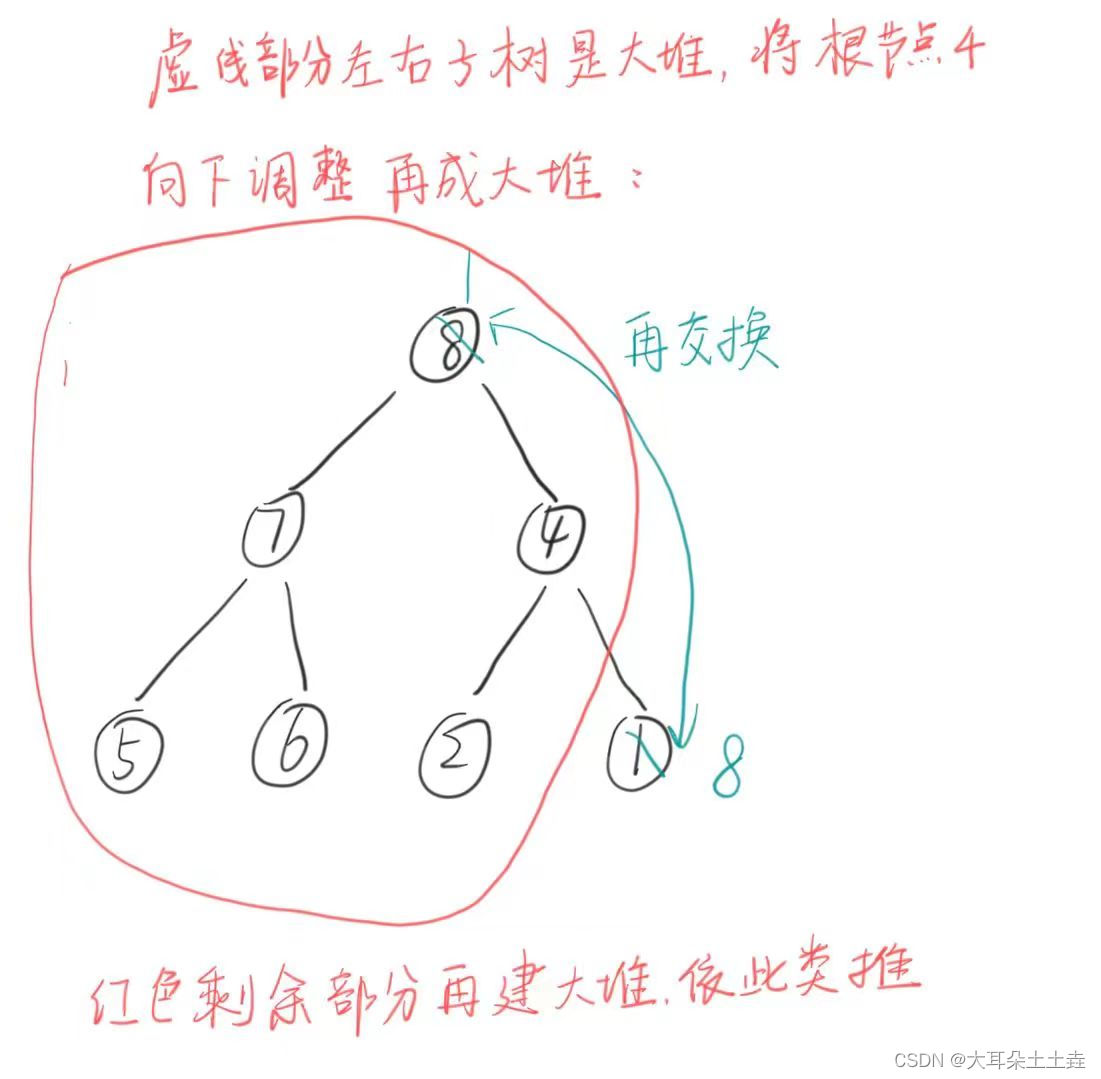
红色剩余部分再建大堆，以此类推。

==堆排序——升序代码如下==：

void HeapSort(int* a, int n)
{
	//向下建堆
	for (int i = (n-1-1)/2; i >= 0; i--)
	{
		AdjustDwon(a, n, i);
	}
	//排序
	
	for (int i = 1; i < n; i++)
	{
		Swap(&a[0], &a[n-i]);
		AdjustDwon(a, n - i, 0);
	}
}

打印结果如下：

学到这里，小伙伴们知道为什么升序要建大堆了吗？
没错关键在于堆向下调整算法实现的前提必须是左右子树都为堆，如果升序建了小堆，那么最开始的数就是最小的值不需要换，我们似乎可以将剩余的数再调整为一个小堆即可，但是我们用什么来调整呢？堆向下调整算法实现吗？那你又是怎么知道剩下的数除了根节点左右子树还是一个堆呢？我们是没办法保证左右子树还是堆的，所以不能利用堆向下调整算法来实现；
而如果一开始调整为大堆就不一样了。我们就可以将根节点也就是最大的数与最后一个数交换，再将出去交换后的前n-1个数向下调整为大堆，因为此时左右子树没有变化还是原来大堆的左右子树依旧是一个堆，可以利用向下调整算法实现，这也就是为什么升序要用大堆，降序要用小堆来实现的原因啦~🥳🥳

四、结语

以上就是选择排序包含的两种排序——直接选择排序和堆排序啦~ 堆排序在之前的博客中有详细讲过不过是建的小堆实现的降序，求最大前k个值，这里我们稍微改了点代码实现建的小堆实现升序；为什么升序要建大堆原因已经在文中详细解析过，大家有什么问题或者想法都可以打在评论区或者私信我🥳🥳完结撒花 ~🎉🎉🎉