【愚公系列】软考中级-软件设计师 056-算法设计与分析(动态规划法和贪心法)
🏆 作者简介,愚公搬代码
🏆《头衔》:华为云特约编辑,华为云云享专家,华为开发者专家,华为产品云测专家,CSDN博客专家,CSDN商业化专家,阿里云专家博主,阿里云签约作者,腾讯云优秀博主,腾讯云内容共创官,掘金优秀博主,51CTO博客专家等。
🏆《近期荣誉》:2022年度博客之星TOP2,2023年度博客之星TOP2,2022年华为云十佳博主,2023年华为云十佳博主等。
🏆《博客内容》:.NET、Java、Python、Go、Node、前端、IOS、Android、鸿蒙、Linux、物联网、网络安全、大数据、人工智能、U3D游戏、小程序等相关领域知识。
🏆🎉欢迎 👍点赞✍评论⭐收藏
🚀前言
动态规划法(Dynamic Programming)和贪心法(Greedy Algorithm)是两种常用的问题求解方法。它们在某些情况下可以互相替代,但在其他情况下则各有优势。
动态规划法是一种将大问题拆分成更小的子问题,并将子问题的解存储起来以避免重复计算的方法。它通常用于求解具有重叠子问题和最优子结构性质的问题。动态规划法的基本思想是,通过解决子问题找到问题的最优解,然后将子问题的解合并起来得到原问题的最优解。动态规划法的时间复杂度通常为O(n^2)或更低,但空间复杂度可能较高。
贪心法是一种贪心地进行选择,每次选择当前最优解的方法。贪心法通常适用于具有贪心选择性质的问题,即每一步都选择当前最优解能够得到全局最优解。贪心法的优点是简单且高效,时间复杂度通常为O(n)。然而,贪心法不能保证求解得到的解是全局最优解,因此在某些情况下可能会得到次优解或错误解。
动态规划法和贪心法的比较可以从以下几个方面进行:
-
解决问题的类型:动态规划法适用于具有重叠子问题和最优子结构性质的问题,而贪心法适用于具有贪心选择性质的问题。
-
解决问题的效率:动态规划法通常需要存储子问题的解,因此在空间上可能比较占用内存。而贪心法不需要存储子问题的解,因此在空间上相对较为节省。在时间效率上,动态规划法的时间复杂度通常为O(n^2)或更低,而贪心法的时间复杂度通常为O(n)。
-
解决问题的保证性:动态规划法可以保证求解得到的解是全局最优解,而贪心法不能保证。因此,在需要保证求解结果为最优解的情况下,应使用动态规划法。
动态规划法和贪心法在解决问题时各有优势,应根据具体问题的性质选择合适的方法。如果问题具有重叠子问题和最优子结构性质,并且需要求解得到的是全局最优解,则应使用动态规划法。如果问题具有贪心选择性质,并且求解的结果不需要是全局最优解,则可以考虑使用贪心法。
🚀一、动态规划法
🔎1.概念
动态规划法(Dynamic Programming):在求解问题中,对于每一步决策,列出各种可能的局部
解,通过决策保留那些有可能达到最优的局部解,丢弃其它局部解,以每一步都是最优解来保证
全局是最优解。
本质也是将复杂的问题划分成一个个子问题,与分治法不同的是分治法中的每个子问题都是相同
的,而动态规划法中的每个子问题间不是相互独立的,并且不全都相同。
此算法会将大量精力放在前期构造表格上面,其会对每一步,列出各种可能的答案,这些答案会
存储起来,最终要得出某个结果时,是通过查询这张表来得到的。动态规划法不但每一步最优,
全局也最优。
总结:动态规划一定是具备了以下三个特点:
- 把原来的问题分解成了几个相似的子问题。(强调“相似子问题”)
- 所有的子问题都只需要解决一次。(强调“只解决一次”)
- 储存子问题的解。(强调“储存”)
🔎2.案例
左下图是使用递归来求解的写法,显然,这是一个非常低效的方法,因为其中有大量的重复计算。并且不满足动态规划的第二个特点:“所有的子问题都只需要解决一次“,这个问题很好解决,我们只需要利用动态规划的第三个特点:”储存子问题的解“就可以了。比如,如果已经计算过Fibonacci(3),那么把结果储存起来,其他地方碰到需要求Fibonacci(3)的时候,就不需要计算,直接调用结果就行。这样做之后,蓝色表示需要进行计算的,白色表示可以直接从存储中取得结果的:
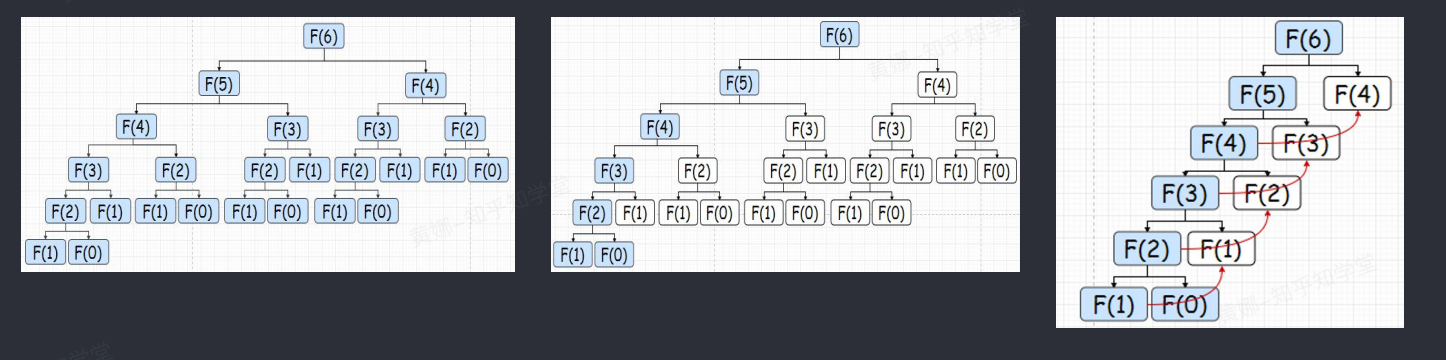
🚀二、贪心法
🔎1.概念
贪心法:总是做出在当前来说是最好的选择,而并不从整体上加以考虑,它所做的每步选择只是当前步骤的局部最优选择,但从整体来说不一定是最优的选择。由于它不比为了寻找最优解而穷尽所有可能解,因此其耗费时间少,一般可以快速得到满意的解,但得不到最优解。
局部贪心,只针对当前的步骤取最优,而非整体考虑。
判断此类算法,就看算法是否是每一步都取最优,并且整体题意没有透露出最终结果是最优的。
🔎2.案例
假设你身上带了足够的1、5、10、20、50、100元面值的钞票。现在您的目标是凑出某个金额w,并且需要用到尽量少的钞票。依据生活经验,我们可以采取这样的策略:能用100的就尽量
用100的,否则尽量用50的……依次类推。在这种策略下,666=6×100+1×50+1×10+1×5+1×1,
共使用了10张钞票。这种策略称为“贪心”:假设我们面对的局面是“需要凑出w”,贪心策略会尽快
让w变得更小。能让w少100就尽量让它少100,这样我们接下来面对的局面就是凑出w-100。长期的生活经验表明,贪心策略是正确的。
如果我们换一组钞票的面值,贪心策略就也许不成立了。如果一个奇葩国家的钞票面
额分别是1、5、11,那么我们在凑出15的时候,贪心策略会出错:15=1×11+4×1 (贪心策略使用
了5张钞票),15=3×5 (正确的策略,只用3张钞票)
贪心策略的纲领是:“尽量使接下来面对的w更小”。这样,贪心策略在w=15的局面时,会优先使用11来把w降到4;但是在这个问题中,凑出4的代价是很高的,必须使用4×1。如果使用了5,w会降为10,虽然没有4那么小,但是凑出10只需要两张5元。在这里我们发现,贪心是一种只考虑眼前情况的策略。
🚀三、动态规划法结合贪心法
如果直接暴力枚举凑出w的方案,明显复杂度过高。太多种方法可以凑出w了,枚举它们的时
间是不可承受的。我们现在来尝试找一下性质。
重新分析刚刚的例子。w=15时,我们如果取11,接下来就面对w=4的情况;如果取5,则接
下来面对w=10的情况。我们发现这些问题都有相同的形式:
“给定w,凑出w所用的最少钞票是多
少张?”接下来,我们用f(n)来表示“凑出n所需的最少钞票数量”。
那么,如果我们取了11,最后的代价(用掉的钞票总数)是多少呢?
明显cost=f(4)+1=4+1=5 ,它的意义是:利用11来凑出15,付出的代价等于f(4)加上自
己这一张钞票。现在我们暂时不管f(4)怎么求出来。
依次类推,马上可以知道:如果我们用5来凑出15,cost就是f(10)+1=2+1=3 。
那么,现在w=15的时候,我们该取那种钞票呢?当然是各种方案中,cost值最低的那一个
!
- 取11:cost=f(4)+1=4+1=5
- 取5: cost=f(10)+1=2+1=3
- 取1: cost=f(14)+1=4+1=5
显而易见,cost值最低的是取5的方案。我们通过上面三个式子,做出了正确的决策!
这给了我们一个至关重要的启示—— f(n) 只与 f(n−1),f(n−5),f(n−11) 相关;更确切地说:
f(n)=min{f(n-1),f(m-5),f(n-11)}+1
这就是DP(动态规划,dynamic programming)将一个问题拆成几个子问题,分别求解这些子问题,即可推断出大问题的解。
🚀四、案例
🔎1.背包问题

题目:考虑一个有n=5个物品的背包问题实例,背包的容量m=10,v(价值)=(6,3,5,4,6),并且w(重量)=(2,2,6,5,4),请问不超过sw(背包能承受的总重)的情况下,最大的放入价值是多少()
【0-1背包问题】就是物品只能放一次,要么放要么不放。(动态规划)
【完全背包问题】物品可以无限放(贪心算法)
【多重背包问题】有n1个物品a1,n2个物品a2,放进背包里,可以转成0-1背包问题,相当于有
🦋1.1 0-1背包问题
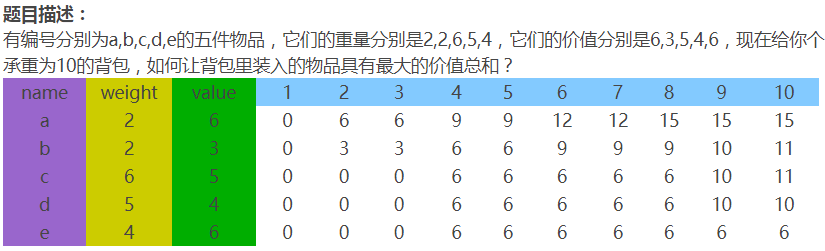
public class Main {
public static void main(String[] args) {
int n = 5;
int[] w = {2,2,6,5,4};
int[] v = {6,3,5,4,6};
int sw = 10;
int[][] dp = new int[n][sw + 1];
for (int i = 0; i <= sw; i++) {
if (i < w[0]) {
dp[0][i] = 0;
} else {
dp[0][i] = v[0];
}
}
for (int i = 1; i < n; i++) {
for (int j = 0; j <= sw; j++) {
if (j < w[i]) {
dp[i][j] = dp[i-1][j];
} else {
dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j- w[i]] + v[i]);
}
}
}
System.out.println(dp[n-1][sw]);
}
}
🦋1.2 完全背包问题
| x1 | x2 | x3 | x4 | x5 | |
|---|---|---|---|---|---|
| 重量w | 2 | 2 | 6 | 5 | 4 |
| 价值v | 6 | 3 | 5 | 4 | 6 |
| 价值重量比V/W | 3 | 1.5 | 0.83 | 0.8 | 1.5 |
按价值重量比从大到小:x1、x2、x5、x3、x4
上界:按重量比从大到小放进去,x1、x2、x5都可以,直到x3时,背包剩余容量2、总价值为15,若将背包填满,则将x3放入重量为2即1/3,此时背包内总价值为15+5*1/3=16.67;下界:每次放入价值最大的,直至放不进去,即6+6=12
🔎2.运输问题
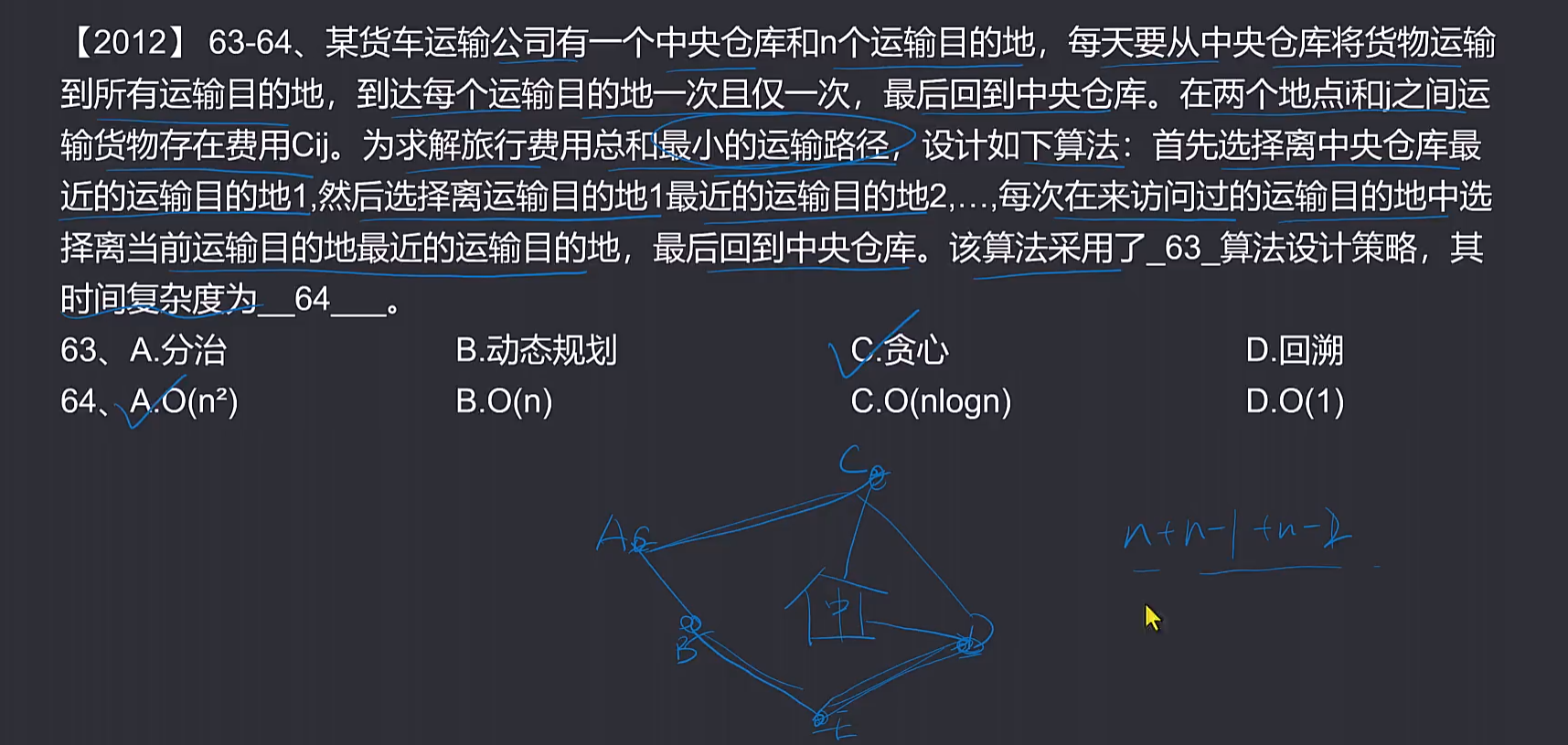
🔎3.消防栓问题
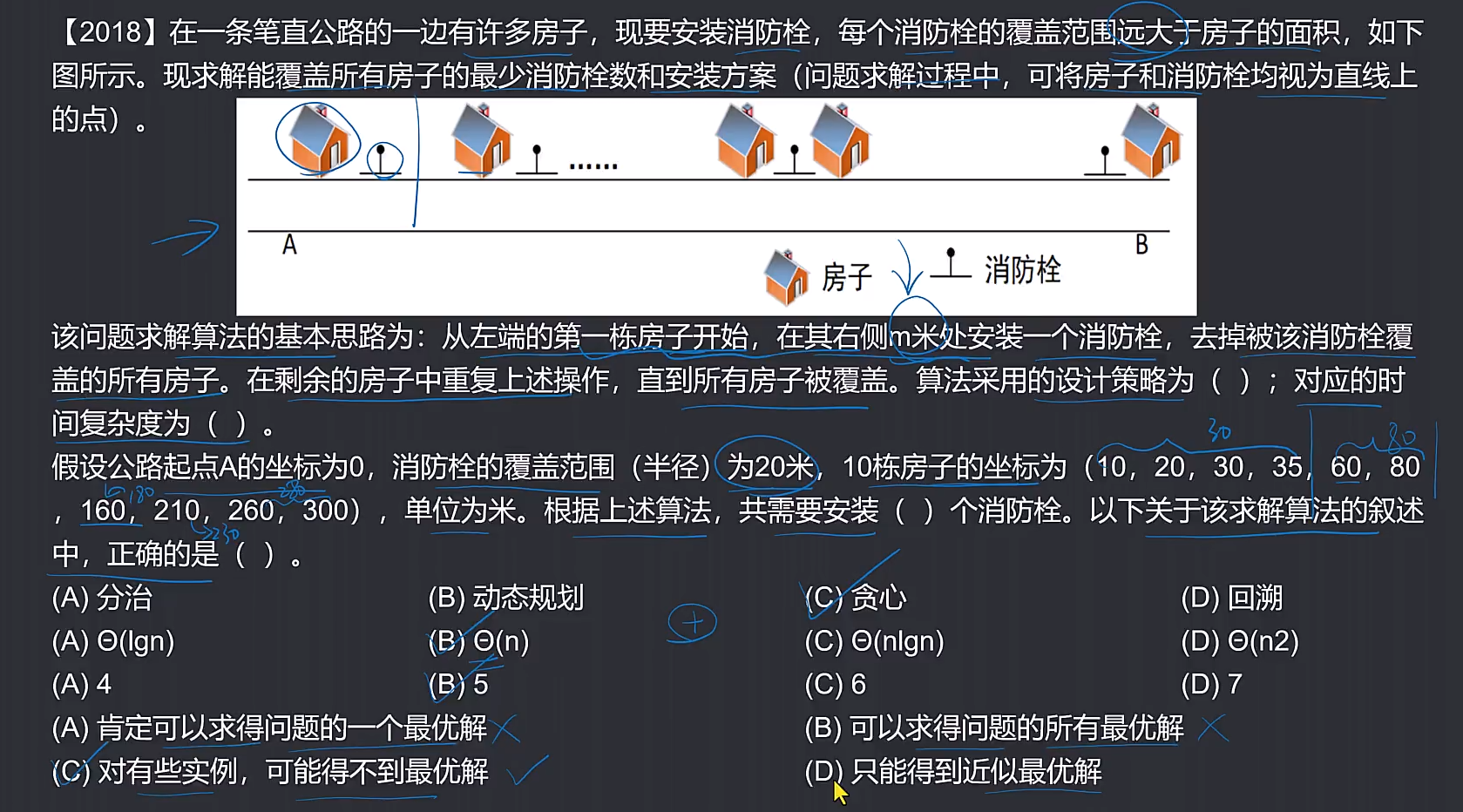
🚀感谢:给读者的一封信
亲爱的读者,
我在这篇文章中投入了大量的心血和时间,希望为您提供有价值的内容。这篇文章包含了深入的研究和个人经验,我相信这些信息对您非常有帮助。
如果您觉得这篇文章对您有所帮助,我诚恳地请求您考虑赞赏1元钱的支持。这个金额不会对您的财务状况造成负担,但它会对我继续创作高质量的内容产生积极的影响。
我之所以写这篇文章,是因为我热爱分享有用的知识和见解。您的支持将帮助我继续这个使命,也鼓励我花更多的时间和精力创作更多有价值的内容。
如果您愿意支持我的创作,请扫描下面二维码,您的支持将不胜感激。同时,如果您有任何反馈或建议,也欢迎与我分享。

再次感谢您的阅读和支持!
最诚挚的问候, “愚公搬代码”
- 点赞
- 收藏
- 关注作者


评论(0)