🏆 作者简介，愚公搬代码
🏆《头衔》：华为云特约编辑，华为云云享专家，华为开发者专家，华为产品云测专家，CSDN博客专家，CSDN商业化专家，阿里云专家博主，阿里云签约作者，腾讯云优秀博主，腾讯云内容共创官，掘金优秀博主，51CTO博客专家等。
🏆《近期荣誉》：2022年度博客之星TOP2，2023年度博客之星TOP2，2022年华为云十佳博主，2023年华为云十佳博主等。
🏆《博客内容》：.NET、Java、Python、Go、Node、前端、IOS、Android、鸿蒙、Linux、物联网、网络安全、大数据、人工智能、U3D游戏、小程序等相关领域知识。
🏆🎉欢迎 👍点赞✍评论⭐收藏

🚀前言

分治法和回溯法都是常见的算法思想，它们在解决问题时有些相似，但也有一些不同之处。

1. 分治法：分治法是将问题分解成更小的子问题，并且递归地解决子问题，最后将子问题的解合并成原问题的解。分治法的基本思想是将问题划分成互不重叠的子问题，然后对子问题进行求解，最后再将子问题的解合并成原问题的解。分治法通常用于解决可以被分为多个独立子问题的问题，如归并排序和快速排序。

2. 回溯法：回溯法也是一种递归算法，它通过试探和回溯的方式搜索问题的解空间。回溯法的基本思想是从问题的一个初始解出发，逐步构造问题的解，当不能继续构造时，就进行回溯，返回上一层继续构造。回溯法通常用于解决在一组可能的解中找出特定解的问题，如八皇后问题和0-1背包问题。

分治法更注重将问题分解成独立的子问题，并通过将子问题的解合并来得到原问题的解，时间复杂度较低；而回溯法更注重尝试和回溯的过程，在解空间中搜索符合条件的解，可能需要遍历所有的可能解，时间复杂度较高。在选择使用哪种算法思想时，需要根据具体问题的特点和要求进行选择。

🚀一、分治法

🔎1.概念

分治法：对于一个规模为n的问题，若该问题可以容易地解决则直接解决；否则将其分解为k个规模较小的子问题，这些子问题互相独立且与原问题形式相同，递归地解决这些子问题，然后将各子问题的解合并得到原问题的解。

步骤：分解(将原问题分解成一系列子问题)——求解(递归地求解各子问题，若子问题足够小，则直接求解)——合并(将子问题的解合并成原问题的解)。

凡是涉及到分组解决的都是分治法(二分查找、归并排序、求阶乘、斐波那契数列等)。

🔎2.案例

🦋2.1 二分查找

二分查找是一种在有序数组中查找特定元素的算法。它的基本思想是通过将数组分成两部分，判断目标元素在哪一部分中，然后继续在该部分中进行查找，直到找到目标元素或者确定目标元素不存在为止。

二分查找的算法如下：

1. 初始化左指针left为0，右指针right为数组长度减1。
2. 循环执行下列步骤：
3. 计算中间位置mid，mid等于左指针left和右指针right之和除以2。
4. 如果目标元素等于中间位置的元素，则返回中间位置。
5. 如果目标元素小于中间位置的元素，则将右指针right更新为mid-1。
6. 如果目标元素大于中间位置的元素，则将左指针left更新为mid+1。
7. 如果循环结束时仍未找到目标元素，则返回-1，表示目标元素不存在。

🦋2.2 归并排序

归并排序是一种分治算法，它将一个数组分成两个子数组，分别对子数组进行排序，然后将两个有序子数组合并为一个有序数组。归并排序的基本思想是将一个大问题分解成两个小问题，然后递归地解决这两个小问题。

归并排序的算法如下：

1. 如果数组长度小于等于1，则返回。
2. 将数组分成两个子数组，分别对每个子数组递归地进行归并排序。
3. 将两个有序子数组合并为一个有序数组。

🦋2.3 求阶乘

求阶乘是一种求解自然数的阶乘的算法。阶乘的定义是n! = n * (n-1) * (n-2) * … * 1。求阶乘的算法可以通过递归的方式来实现，即将问题分解为更小的子问题。

求阶乘的算法如下：

1. 如果n等于0或1，则返回1。
2. 否则，将问题分解为求解(n-1)!，然后将结果乘以n。

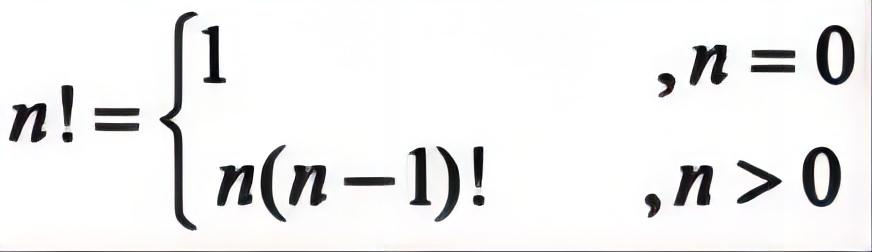
🦋2.4 斐波那契数列

斐波那契数列是一种数列，其前两个数字为0和1，后续数字为前两个数字之和。斐波那契数列的递推公式为f(n) = f(n-1) + f(n-2)，其中f(0) = 0，f(1) = 1。

求解斐波那契数列的算法可以通过递归的方式来实现，即将问题分解为求解f(n-1)和f(n-2)。

求解斐波那契数列的算法如下：

1. 如果n等于0，则返回0。
2. 如果n等于1，则返回1。
3. 否则，将问题分解为求解f(n-1)和f(n-2)，然后将结果相加。

🚀二、回溯法

🔎1.概念

回溯法（Backtracking）是一种选优的暴力搜寻法。但是，由于暴力，回溯法的时间复杂度较高，又称为试探法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。

一般用于解决迷宫类的问题。其思路不难理解，想象一下你在走一个迷宫，当在一个路口有A， B， C 三条岔路的时候你要怎么办呢？ 大家可以很容易地想到先尝试道路A， 如果走不通就回到这个路口尝试道路B，如果还走不通就尝试道路C，这就是一个典型地应用回溯法的例子。如果将目光着眼于整个迷宫，就可以发现这个迷宫其实就是一颗多叉树，每个路口就是一个节点，每个路口的岔路就是这个节点的子树，在这颗多叉树上应用深度优先搜索就是回溯法。

🔎2.案例

回溯法是一种递归的算法思想，常用于解决一些组合问题，比如求解排列、组合、子集等。

下面是一个回溯法的经典案例——八皇后问题。

八皇后问题是一个经典的问题，要求在一个8×8的棋盘上放置8个皇后，使得任意两个皇后都不能在同一行、同一列或同一对角线上。

具体的回溯算法思路如下：

1. 定义一个长度为8的数组queen，用来记录每行皇后的列位置。
2. 从第一行开始，逐行放置皇后。
3. 对于每一行，依次尝试在每一列放置皇后。
4. 判断当前位置是否与已放置的皇后冲突，如果冲突则尝试下一列。
5. 如果找到一个合适的位置，则记录当前位置，并递归地继续放置下一行的皇后。
6. 如果找不到一个合适的位置，则返回上一行，回溯到上一个位置继续尝试下一列。
7. 当放置完8个皇后后，得到一个解，输出解的位置。

以下是一个python代码实现：

def solve_n_queens():
    queen = [-1] * 8  # 存放每行皇后的列位置
    
    def is_conflict(row, col):
        # 判断当前位置与已放置的皇后是否冲突
        for i in range(row):
            if queen[i] == col or \
                queen[i] - i == col - row or \
                queen[i] + i == col + row:
                return True
        return False
    
    def backtrack(row):
        # 回溯函数
        if row == 8:
            # 找到一个解，输出位置
            print(queen)
            return
        
        for col in range(8):
            if not is_conflict(row, col):
                # 当前位置不冲突，记录位置并继续放置下一行的皇后
                queen[row] = col
                backtrack(row + 1)
                # 回溯，尝试下一列
                queen[row] = -1
    
    backtrack(0)  # 从第一行开始放置皇后


solve_n_queens()

运行上述代码，可以得到八皇后问题的全部解：

[0, 4, 7, 5, 2, 6, 1, 3]
[0, 5, 7, 2, 6, 3, 1, 4]
[0, 6, 3, 5, 7, 1, 4, 2]
[0, 6, 4, 7, 1, 3, 5, 2]
[1, 3, 5, 7, 2, 0, 6, 4]
[1, 4, 6, 0, 2, 7, 5, 3]
[1, 4, 6, 3, 0, 7, 5, 2]
[1, 5, 0, 6, 3, 7, 2, 4]
...

🚀感谢：给读者的一封信

亲爱的读者，

我在这篇文章中投入了大量的心血和时间，希望为您提供有价值的内容。这篇文章包含了深入的研究和个人经验，我相信这些信息对您非常有帮助。

如果您觉得这篇文章对您有所帮助，我诚恳地请求您考虑赞赏1元钱的支持。这个金额不会对您的财务状况造成负担，但它会对我继续创作高质量的内容产生积极的影响。

我之所以写这篇文章，是因为我热爱分享有用的知识和见解。您的支持将帮助我继续这个使命，也鼓励我花更多的时间和精力创作更多有价值的内容。

如果您愿意支持我的创作，请扫描下面二维码，您的支持将不胜感激。同时，如果您有任何反馈或建议，也欢迎与我分享。

再次感谢您的阅读和支持！

最诚挚的问候， “愚公搬代码”