🏆 作者简介，愚公搬代码
🏆《头衔》：华为云特约编辑，华为云云享专家，华为开发者专家，华为产品云测专家，CSDN博客专家，CSDN商业化专家，阿里云专家博主，阿里云签约作者，腾讯云优秀博主，腾讯云内容共创官，掘金优秀博主，51CTO博客专家等。
🏆《近期荣誉》：2023年华为云十佳博主，2022年CSDN博客之星TOP2，2022年华为云十佳博主等。
🏆《博客内容》：.NET、Java、Python、Go、Node、前端、IOS、Android、鸿蒙、Linux、物联网、网络安全、大数据、人工智能、U3D游戏、小程序等相关领域知识。
🏆🎉欢迎 👍点赞✍评论⭐收藏

🚀前言

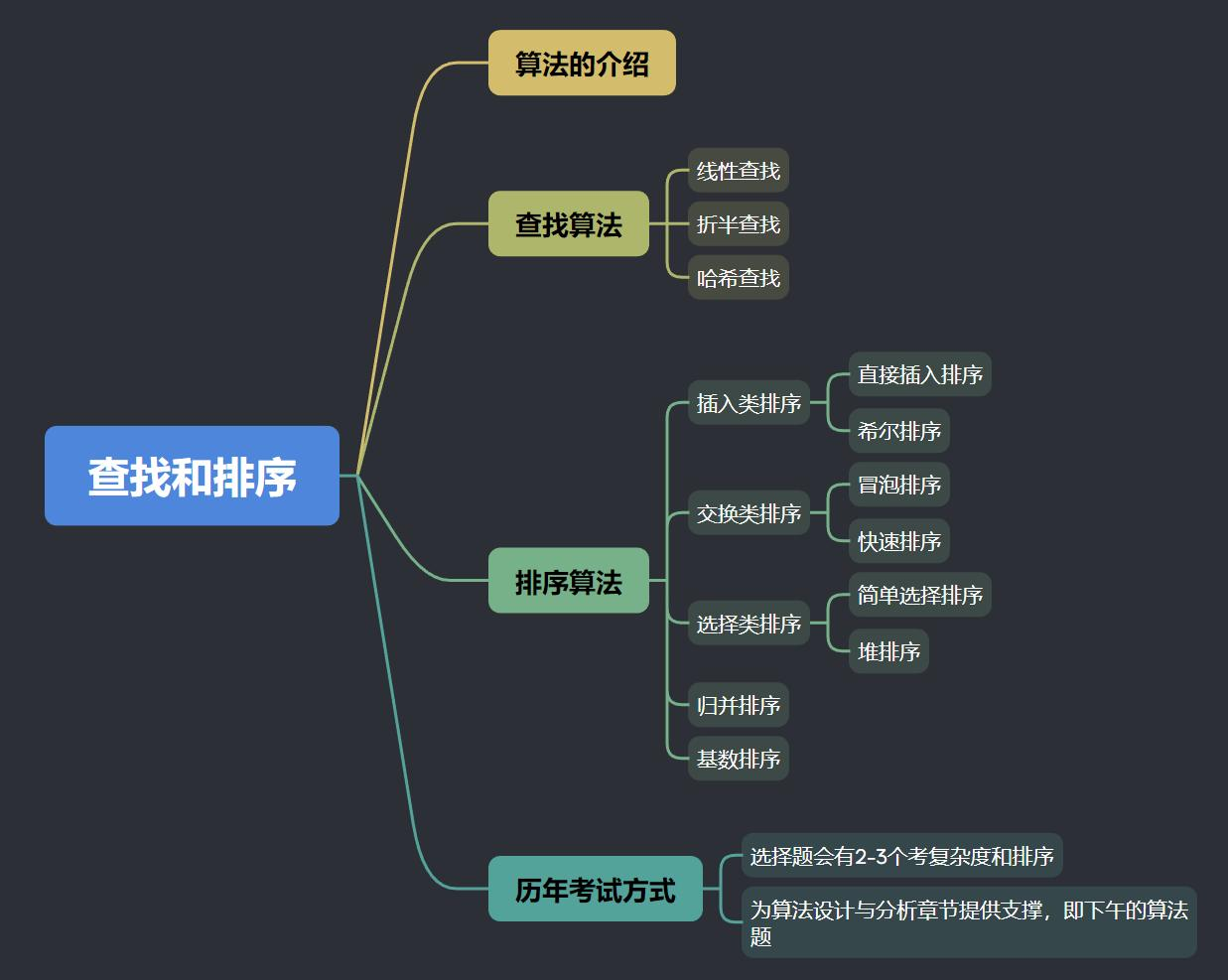
数据结构中的查找算法是指在一个给定的数据结构中，寻找特定元素的过程。常见的查找算法有线性查找、二分查找、哈希查找等。

1. 线性查找（Sequential Search）：从数据结构的第一个元素开始，逐个比较元素，直到找到目标元素或者搜索完整个数据结构。

2. 折半(二分)查找（Binary Search）：针对已经排序的数据结构，将目标元素与中间位置的元素进行比较，如果小于中间元素，则在左半部分继续查找；如果大于中间元素，则在右半部分继续查找；直到找到目标元素或者左右边界相交。

3. 哈希查找（Hash Search）：通过哈希函数将元素映射到数组中的某个位置，然后根据该位置查找目标元素。哈希查找的时间复杂度为常数级别，但需要额外的空间存储哈希表。

除了以上三种常见的查找算法，还有其他一些高级的查找算法，例如插值查找、二叉查找树、B树等。这些算法的选择取决于数据结构的性质和具体的查找需求。

🚀一、查找算法

🔎1.算法基础

🦋1.1 算法概念

算法是一组有序的操作指令，用于解决特定问题或完成特定任务。算法描述了问题的输入和输出，以及在给定输入时如何通过一系列步骤来产生所需的输出。算法可以用来解决各种问题，包括数学问题、计算问题、优化问题等。在计算机科学中，算法是计算机程序的基础，它指导计算机执行特定的计算和操作。一个好的算法应该具有正确性（能够产生正确的输出）、效率（能够在合理的时间内完成计算）和易读性（易于理解和实现）。简单的说就是某个问题的解题思路。

🦋1.2 算法的复杂度

算法的复杂度是衡量算法执行效率的一个指标，通常用时间复杂度和空间复杂度来描述。

1. 时间复杂度：描述随着问题规模的增大，算法执行时间的增长趋势。常见的时间复杂度包括：

   • 常数时间复杂度 O(1)：无论问题规模多大，算法的执行时间都不会随之增长。
   • 线性时间复杂度 O(n)：算法的执行时间与问题规模呈线性关系。
   • 对数时间复杂度 O(log n)：算法的执行时间与问题规模的对数呈线性关系。
   • 平方时间复杂度 O(n^2)：算法的执行时间与问题规模的平方呈线性关系。
   • 指数时间复杂度 O(2^n)：算法的执行时间与问题规模的指数呈线性关系。

2. 空间复杂度：描述算法执行中所需的额外空间随问题规模增大的趋势。常见的空间复杂度包括：

   • 常数空间复杂度 O(1)：算法的额外空间不随问题规模的增大而变化。
   • 线性空间复杂度 O(n)：算法的额外空间与问题规模呈线性关系。
   • 对数空间复杂度 O(log n)：算法的额外空间与问题规模的对数呈线性关系。
   • 平方空间复杂度 O(n^2)：算法的额外空间与问题规模的平方呈线性关系。
   • 指数空间复杂度 O(2^n)：算法的额外空间与问题规模的指数呈线性关系。

算法的复杂度分析可以帮助我们评估算法的执行效率，并选择合适的算法来解决问题。通常情况下，我们希望选择时间复杂度低且空间复杂度较小的算法。

常见的对算法执行所需时间的度量：O(1)<O(log2n)<O(n)<O(nlog2n)<O(n²)<O(n³)<O(2ⁿ)<O(n!)

上述的时间复杂度，经常考到，需要注意的是，时间复杂度是一个大概的规模表示，一般以循环次数表示，O(n)说明执行时间是n的正比，另外，log对数的时间复杂度一般在查找二叉树的算法中出现。渐进符号O表示一个渐进变化程度，实际变化必须小于等于O括号内的渐进变化程度。

🔎2.查找算法

🦋2.1 线性查找

线性查找是一种简单直接的查找算法，也称为顺序查找。它通过遍历待查找的数据集，逐个比较数据元素与目标值，直到找到目标值或遍历完整个数据集为止。

线性查找的基本思路如下：

1. 从第一个数据元素开始，逐个遍历数据集中的元素。
2. 每次比较当前元素与目标值是否相等，如果相等则返回当前位置，表示找到目标值。
3. 如果遍历完整个数据集仍未找到目标值，则返回-1，表示未找到目标值。

下面是使用Python实现的线性查找算法的示例代码：

def linear_search(arr, target):
    for i in range(len(arr)):
        if arr[i] == target:
            return i  # 返回目标值的位置
    return -1  # 未找到目标值

# 测试线性查找算法
arr = [3, 5, 2, 8, 9, 4, 1]
target = 9
result = linear_search(arr, target)
if result != -1:
    print("目标值在位置", result)
else:
    print("未找到目标值")

在最坏情况下，线性查找的时间复杂度为O(n)，其中n为数据集的大小。因为需要逐个遍历数据元素，所以当数据集较大时，线性查找的效率相对较低。因此在实际应用中，当数据集较大时，可以考虑使用更高效的查找算法，如二分查找、哈希查找等。

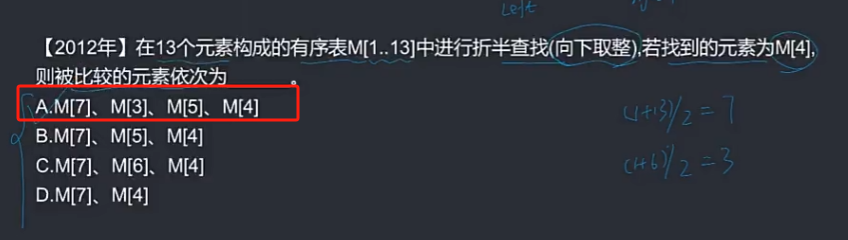
🦋2.2 折半(二分)查找

折半查找（也称为二分查找）是一种高效的查找算法，常用于有序数组中查找某个特定元素的位置。

折半查找的基本思想是首先确定待查找区间的中间位置，然后将待查找元素与中间位置的元素进行比较。如果待查找元素等于中间位置的元素，则查找成功，返回中间位置；如果待查找元素小于中间位置的元素，则在中间位置的左侧区间继续查找；如果待查找元素大于中间位置的元素，则在中间位置的右侧区间继续查找。重复以上步骤直至找到目标元素或待查找区间为空。

折半(二分)查找是一种基于有序数组的查找算法，其时间复杂度为O(logn)。其基本思路如下：

1. 初始化左边界和右边界，将左边界设为0，将右边界设为数组长度减1。
2. 取中间位置的元素，与目标元素进行比较。
3. 如果中间元素等于目标元素，则返回中间元素的索引。
4. 如果中间元素大于目标元素，则在左半部分继续查找，将右边界更新为中间元素的前一个索引。
5. 如果中间元素小于目标元素，则在右半部分继续查找，将左边界更新为中间元素的后一个索引。
6. 重复步骤2至5，直到左边界大于右边界，表示查找失败。

下面是一个使用Python实现折半查找的例子：

def binary_search(arr, target):
    left = 0
    right = len(arr) - 1
    
    while left <= right:
        mid = (left + right) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    
    return -1  # 目标元素不存在

# 测试案例
arr = [1, 3, 5, 7, 9, 11, 13]
target = 7
result = binary_search(arr, target)
if result != -1:
    print("目标元素在数组中的索引为", result)
else:
    print("目标元素不存在数组中")

我们首先定义了一个二分查找函数binary_search，它接受一个有序数组arr和目标元素target作为输入。然后我们在数组中查找目标元素并返回其索引，如果目标元素不存在，则返回-1。

时间复杂度分析：

折半查找每次将当前查找范围缩小一半，因此查找的次数取决于查找范围的大小，即查找次数为 logn (以2为底)。因此，折半查找的时间复杂度为O(logn)。

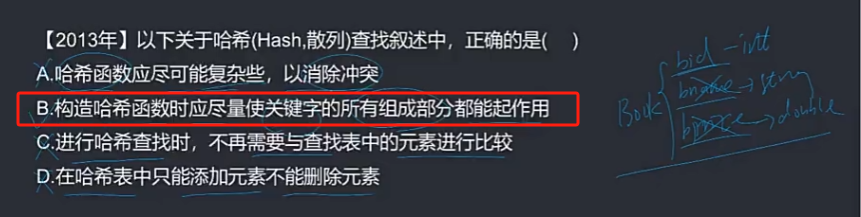
🦋2.3 哈希查找

哈希查找（Hash Search）也被称为散列查找，是一种根据关键字直接进行访问的查找技术，具有快速查找的特点。哈希查找的基本思路是通过哈希函数将关键字映射到一个固定的位置，称为哈希地址。利用哈希地址来直接访问目标数据。

下面是一个使用Python实现哈希查找的示例代码：

class HashTable:
    def __init__(self, size):
        self.size = size
        self.table = [[] for _ in range(size)]   # 创建一个包含size个空列表的列表

    def hash_function(self, key):
        return key % self.size   # 使用取余来进行哈希映射

    def insert(self, key, value):
        hash_value = self.hash_function(key)
        self.table[hash_value].append((key, value))   # 将关键字和值以元组的形式存储到哈希地址对应的列表中

    def search(self, key):
        hash_value = self.hash_function(key)
        for k, v in self.table[hash_value]:
            if k == key:
                return v    # 如果找到关键字，返回对应的值
        return None    # 如果没找到关键字，返回None


# 示例代码
hash_table = HashTable(10)

hash_table.insert(1, 'apple')
hash_table.insert(2, 'banana')
hash_table.insert(11, 'cherry')

print(hash_table.search(1))   # 输出：apple
print(hash_table.search(2))   # 输出：banana
print(hash_table.search(11))  # 输出：cherry
print(hash_table.search(3))   # 输出：None

上述代码中，我们创建了一个哈希表（HashTable）类，其中包含以下几个方法：

• __init__(self, size)：初始化哈希表，指定哈希表的大小。
• hash_function(self, key)：哈希函数，用于将关键字映射到哈希地址。
• insert(self, key, value)：插入方法，将关键字和值插入到哈希表中。
• search(self, key)：查找方法，根据关键字查找对应的值。

时间复杂度：

• 插入和查找的时间复杂度都为O(1)，即常数时间复杂度。这是因为哈希函数的设计使得每个关键字都能映射到唯一的哈希地址，因此可以直接在哈希地址对应的列表中进行操作。在没有冲突的情况下，插入和查找操作都只需要一次哈希映射和一次遍历操作即可完成。

☀️2.3.1 冲突解决

案例分析：

🌈2.3.1.1 线性探测法

哈希查找中的线性探测法是一种解决哈希冲突的方法。当在哈希表中插入一个元素时，如果发生冲突，即要插入的位置已经被占用，线性探测法会顺序地往后查找，直到找到一个空槽或者遍历完整个哈希表。

具体的插入过程如下：

1. 使用哈希函数计算要插入元素的哈希值，得到在哈希表中的初始位置。
2. 如果初始位置为空槽，则直接将元素插入到该位置。
3. 如果初始位置已经被占用，即发生冲突，就顺序地往后查找，直到找到一个空槽或者遍历完整个哈希表。
4. 如果找到了空槽，则将元素插入到该空槽中。
5. 如果遍历完整个哈希表，仍然没有找到空槽，表示哈希表已满，插入失败。

在查找元素时，也使用相同的过程：

1. 使用哈希函数计算要查找元素的哈希值，得到在哈希表中的初始位置。
2. 如果初始位置为空槽，则表示要查找的元素不存在。
3. 如果初始位置不为空槽，需要顺序地往后查找，直到找到目标元素或者遍历完整个哈希表。
4. 如果找到了目标元素，则返回其位置。
5. 如果遍历完整个哈希表，仍然没有找到目标元素，则表示要查找的元素不存在。

线性探测法的优点是实现简单，插入和查找的平均时间复杂度都是O(1)。然而，它也有一些缺点。当哈希表中的装载因子（已占用槽数目与总槽数目的比值）较大时，会导致冲突的概率增加，从而使得线性探测法的性能下降。另外，线性探测法会产生聚集效应，即冲突的元素会集中在一起，导致哈希表中的空槽较少，进而影响插入和查找的效率。

知识点额外补充：一致性哈希

一致性哈希是一种解决分布式系统中数据分散和负载均衡的方法。在分布式系统中，数据通常按照某种规则被分散存储在不同的节点上，为了快速定位到存储数据的节点，需要使用哈希函数来将数据的键映射到一个节点的位置。然而，当系统中的节点发生变化（如节点的加入、删除或故障）时，传统的哈希方法需要重新计算所有的映射，导致大量数据的迁移工作，增加系统的开销和复杂性。

一致性哈希通过引入虚拟节点的概念，解决了传统哈希方法的这个问题。具体来说，一致性哈希将哈希空间（通常是一个固定的范围，如0-2^32）划分成一个圆环，并将节点和数据键使用哈希函数映射到圆环上的位置。每个节点在圆环上有多个虚拟节点，通过增加虚拟节点，可以使节点在哈希环上分布更加均匀。

当需要存储数据时，通过哈希函数将数据的键映射到圆环上的一个位置，然后沿着圆环顺时针查找，找到离该位置最近的节点，即为数据存储的节点。当节点发生变化时，只需要迁移受影响的数据部分，对于其他数据则不需要变动。

一致性哈希的优点包括：

• 节点的动态变化对数据的迁移影响较小，减少了系统的开销和复杂性。
• 数据在节点上的分布更加均匀，提高了系统的负载均衡性。
• 在节点变化时，只需要迁移少量数据，减少了数据迁移的开销。

一致性哈希在分布式存储、负载均衡、缓存系统等领域得到广泛应用。

🌈2.3.1.2 伪随机数法

伪随机数法是当哈希函数将多个键映射到同一个索引位置时，伪随机数法可以通过生成一系列伪随机数来确定下一个可用的位置。

伪随机数法的基本思想是，在冲突的位置上，通过计算一个伪随机数来确定下一个可用的位置。这个伪随机数可以是基于当前冲突位置和键的某种计算方式得出的结果。一旦找到了下一个可用的位置，就可以将键值对插入到该位置上。

伪随机数法的一个优点是，可以较好地解决哈希冲突问题，减少冲突的次数，提高查找效率。然而，伪随机数法也有一些限制和注意事项。首先，生成伪随机数的计算方式需要被设计得足够复杂，以保证生成的位置能够更加均匀地分布在哈希表中，避免过多的冲突。其次，伪随机数生成的效率可能较低，特别是在哈希表规模较大的情况下。因此，在实际应用中，需要根据具体的需求和场景选择适合的哈希冲突解决方法。

🌈2.3.1.3 再散列法

再散列法（Rehashing）它是在原有的哈希表中再次进行哈希运算，以找到一个新的位置存储冲突的元素。

具体来说，当发生冲突时，再散列法会使用不同的哈希函数或使用原有哈希函数的不同参数，将冲突元素重新计算哈希值，然后找到一个新的位置存储。

再散列法可以多次进行再散列，直到找到一个不冲突的位置为止。常见的再散列方法包括线性探测再散列、平方探测再散列、双散列等。

再散列法的优点是简单、易于实现，并且在处理小规模数据集时表现良好。然而，当数据量大或者哈希函数选择不当时，再散列法可能导致严重的哈希冲突问题，使查询效率下降。因此，在设计哈希表时，需要选择合适的哈希函数和再散列方法，以避免冲突。

🚀感谢：给读者的一封信

亲爱的读者，

我在这篇文章中投入了大量的心血和时间，希望为您提供有价值的内容。这篇文章包含了深入的研究和个人经验，我相信这些信息对您非常有帮助。

如果您觉得这篇文章对您有所帮助，我诚恳地请求您考虑赞赏1元钱的支持。这个金额不会对您的财务状况造成负担，但它会对我继续创作高质量的内容产生积极的影响。

我之所以写这篇文章，是因为我热爱分享有用的知识和见解。您的支持将帮助我继续这个使命，也鼓励我花更多的时间和精力创作更多有价值的内容。

如果您愿意支持我的创作，请扫描下面二维码，您的支持将不胜感激。同时，如果您有任何反馈或建议，也欢迎与我分享。

再次感谢您的阅读和支持！

最诚挚的问候， “愚公搬代码”