【愚公系列】软考中级-软件设计师 020-数据结构(图)
🏆 作者简介,愚公搬代码
🏆《头衔》:华为云特约编辑,华为云云享专家,华为开发者专家,华为产品云测专家,CSDN博客专家,CSDN商业化专家,阿里云专家博主,阿里云签约作者,腾讯云优秀博主,腾讯云内容共创官,掘金优秀博主,51CTO博客专家等。
🏆《近期荣誉》:2023年华为云十佳博主,2022年CSDN博客之星TOP2,2022年华为云十佳博主等。
🏆《博客内容》:.NET、Java、Python、Go、Node、前端、IOS、Android、鸿蒙、Linux、物联网、网络安全、大数据、人工智能、U3D游戏、小程序等相关领域知识。
🏆🎉欢迎 👍点赞✍评论⭐收藏
🚀前言
图是一种非线性数据结构,它由节点(也称为顶点)和连接这些节点的边组成。图可以用来表示各种关系和连接,比如网络拓扑、社交网络、地图等等。图的节点可以包含任意类型的数据,而边则表示节点之间的关系。图有两种常见的表示方法:邻接矩阵和邻接表。
邻接矩阵是一个二维数组,其中的元素表示节点之间是否有连接。如果节点 i 和节点 j 之间有连接,则邻接矩阵中的第 i 行第 j 列的元素为 1,否则为 0。邻接矩阵的优点是查询两个节点之间是否有连接的时间复杂度为 O(1),但是缺点是当图中节点的数量很大时,矩阵的存储空间会非常庞大。
邻接表是一种链表的数组,数组中的每个元素对应一个节点,链表中的每个节点记录了与该节点直接相连的节点。邻接表的优点是存储空间相对较小,缺点是在查询两个节点之间是否有连接时需要遍历链表,时间复杂度可能较高。
图具有很多重要的算法,比如深度优先搜索(DFS)和广度优先搜索(BFS)用于遍历图,最短路径算法用于找到两个节点之间的最短路径,拓扑排序用于解决依赖关系问题等等。图的数据结构在计算机科学中有着广泛的应用。

🚀一、图
🔎1.图的概念
| 概念 | 定义 |
|---|---|
| 无向图 | 图的节点之间连接线是没有箭头的,不分方向。 |
| 有向图 | 图的节点之间连接线是箭头,区分A到B,和B到A是两条线。 |
| 完全图 | 无向完全图中,节点两两之间都有连线,n个结点的连线数为(n-1)+(n-2)+…+1=n*(n-1)/2;有向完全图中,节点两两之间都有互通的两个箭头,n个节点的连线数为n*(n-1)。 |
| 度、出度和入度 | 顶点的度是关联与该顶点的边的数目。在有向图中,顶点的度为出度和入度之和。出度是以该顶点为起点的有向边的数目。入度是以该顶点为终点的有向边的数目。 |
| 路径 | 存在一条通路,可以从一个顶点到达另一个顶点,有向图的路径也是有方向的。 |
| 连通图和连通分量 | 针对无向图。若从顶点v到顶点u之间是有路径的,则说明v和u之间是连通的,若无向图中任意两个顶点之间都是连通的,则称为连通图。 |
| 强连通图的强连通分量 | 针对有向图。若有向图任意两个顶点间都相互存在路径,则称为强连通图。有向图中的极大联通子图称为其强联通分量。 |
| 网 | 边带权值的图称为网。 |
🔎2.图的存储
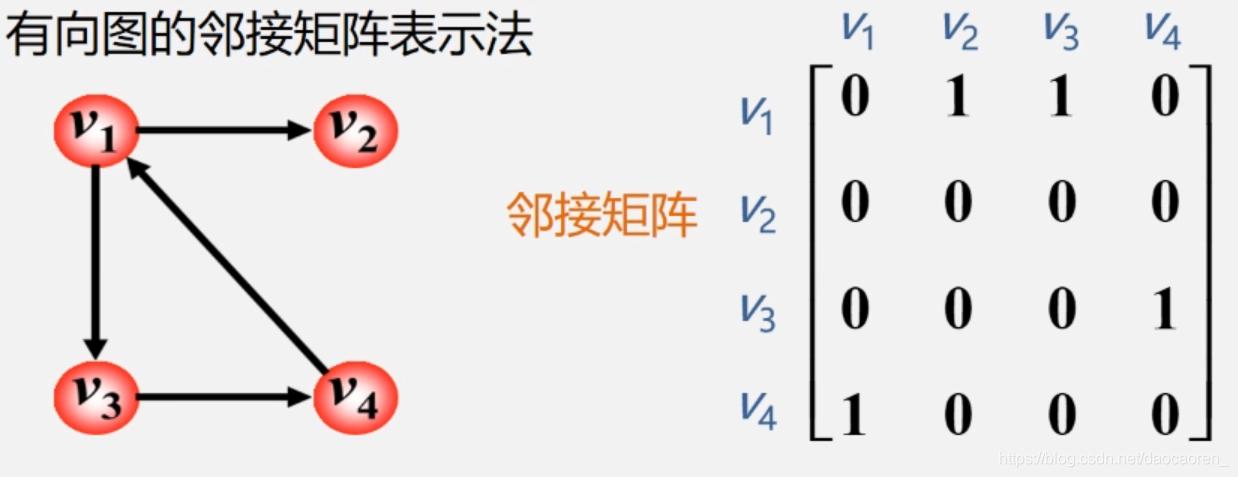
🦋2.1 邻接矩阵
图的存储邻接矩阵是一种常见的图表示方式,适用于稠密图(边数接近于顶点数的平方)的存储。
邻接矩阵是一个二维数组,其中行和列表示图中的顶点,数组元素表示顶点之间的边或者权重。
具体的做法如下:
- 创建一个大小为VxV的二维数组,其中V是图中顶点的个数。
- 初始化数组的所有元素为0,表示顶点之间没有边。
- 对于有边连接的两个顶点u和v,设定数组中的元素a[u][v]和a[v][u]为1,表示顶点u和v之间有边。
- 如果图是带权重的,可以将数组中的元素a[u][v]和a[v][u]设为边的权重值。
邻接矩阵的存储优点是可以快速判断两个顶点之间是否有边,时间复杂度为O(1)。但是对于稀疏图(边数远小于顶点数的平方)来说,邻接矩阵会浪费大量的空间。
在使用邻接矩阵存储图时,需要考虑到数组的大小限制和边的存储方式。通常可以使用二维数组、动态数组或稀疏矩阵等数据结构来实现邻接矩阵的存储。

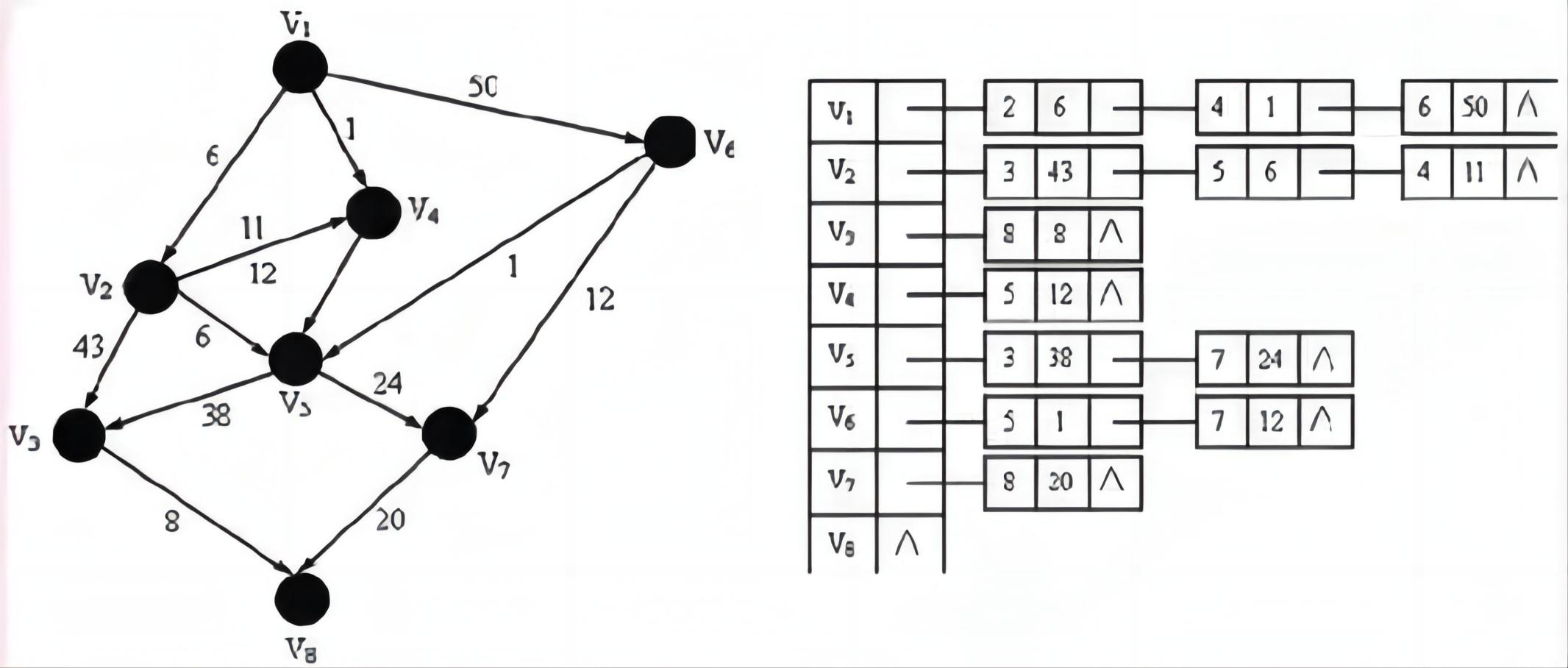
🦋2.2 邻接表
图的邻接表是一种常用的图的存储方式,它使用一个数组来存储图中的每个顶点,数组中的每个元素是一个链表,链表中存储了与该顶点相邻的顶点。
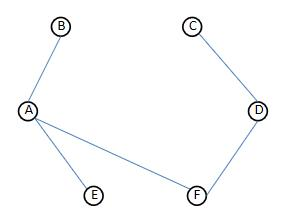
例如,考虑以下无向图:
A -- B -- C
| |
D -- E -- F
可以使用邻接表来表示这个图:
顶点 A: B, D
顶点 B: A, C
顶点 C: B, F
顶点 D: A, E
顶点 E: D, F
顶点 F: C, E
在邻接表中,每个顶点对应一个链表,链表中的每个节点表示与该顶点相邻的另一个顶点。例如,顶点 A 对应的链表中有节点 B 和 D,表示 A 与 B 和 D 相邻。同样地,顶点 B 对应的链表中有节点 A 和 C,表示 B 与 A 和 C 相邻。
邻接表的优点是可以有效地表示稀疏图,节省了存储空间。同时,邻接表也可以方便地找到一个顶点的所有邻接顶点,因为它们都存储在同一个链表中。但是,对于密集图,邻接表的查询效率可能较低,因为需要遍历链表来寻找相邻顶点。

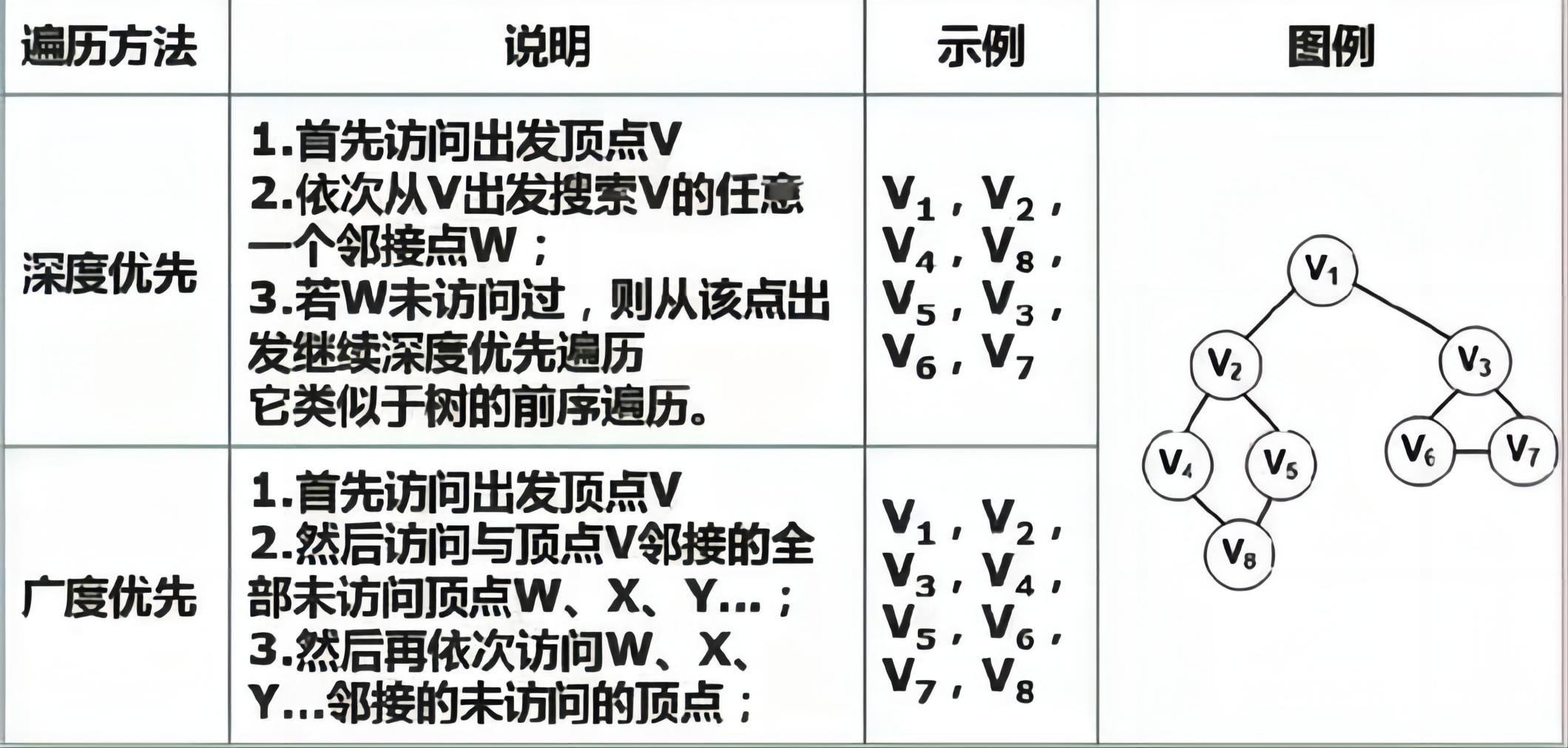
🔎3.图的遍历
图的遍历是指按照某种规则访问图中的所有节点。图的遍历分为深度优先搜索(DFS)和广度优先搜索(BFS)两种常见的方法。
1、深度优先搜索(DFS):
DFS是一种递归的搜索方法。它从图中的某个节点开始,然后递归地访问该节点的所有邻接节点,直到所有可达的节点都被访问一次。然后,返回到上一个节点,尝试访问它的其他邻接节点,直到遍历完整个图。
DFS的过程可以使用栈来实现,首先将起始节点入栈,然后弹出栈顶节点,并将其标记为已访问,接着将该节点的所有未访问的邻接节点入栈。重复这个过程,直到栈为空。
2、广度优先搜索(BFS):
BFS使用队列来实现。它从图的某个节点开始,首先将该节点入队列,然后访问该节点的所有邻接节点,并将其入队列。接下来,从队列中取出一个节点并访问它的所有邻接节点,将它们入队列。重复这个过程,直到队列为空。
DFS和BFS都可以用来遍历无向图和有向图。它们之间的主要区别在于访问节点的顺序不同,DFS优先访问深度较大的节点,而BFS优先访问离起始节点近的节点。
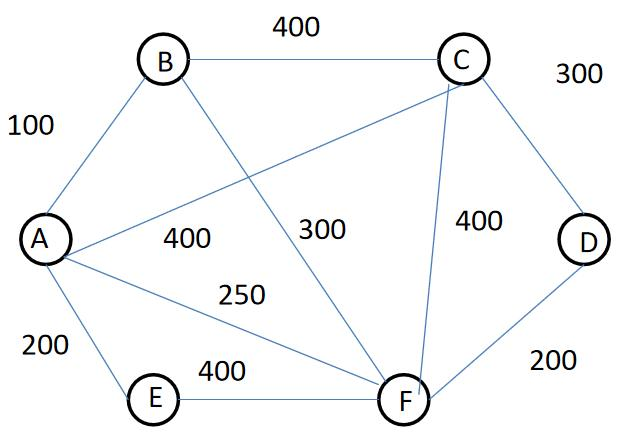
🔎4.图的最小生成树
最小生成树是一个连通无向图的生成树中,边的权值和最小的生成树。图的最小生成树算法有普里姆(Prim)算法和克鲁斯卡尔(Kruskal)算法。
普里姆算法:
- 选择一个起始顶点,将起始顶点标记为已访问;
- 在已访问的顶点集合中,选择一条与未访问顶点相连的最小权值边,并将该边的另外一个顶点标记为已访问;
- 重复步骤2,直到所有顶点都标记为已访问,最小生成树构建完成。
克鲁斯卡尔算法:
- 将图中的所有边按照权值从小到大排序;
- 依次选择权值最小的边,并判断该边的两个顶点是否属于不同的连通分量。如果属于不同的连通分量,则将该边加入最小生成树,否则舍弃该边;
- 重复步骤2,直到最小生成树的边数等于图的顶点数减一。
这两种算法都是局部最优原则,所以都是贪心法算法,并且没有谁的效率高谁的效率差,因为克鲁斯卡尔算法是数边的,所以边越多,它算起来越麻烦。

🔎5.图的拓扑序列
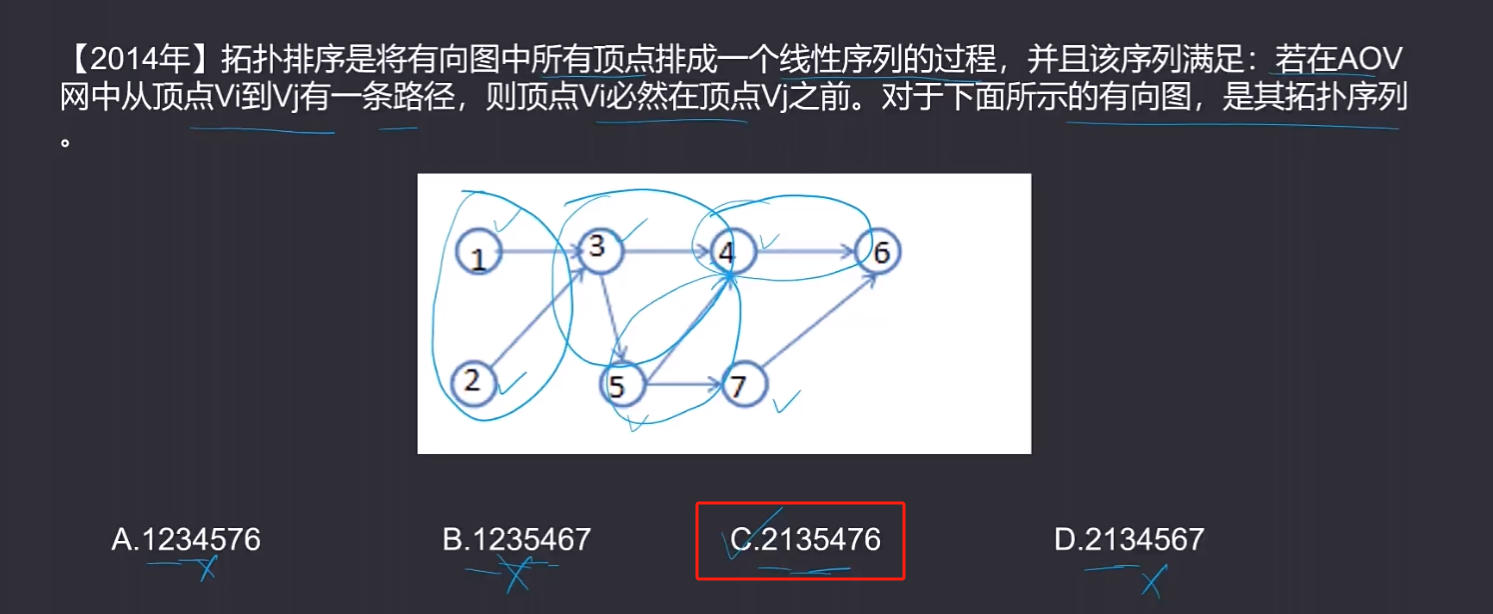
图的拓扑序列是指一个有向无环图(DAG)的顶点的一种线性排序,使得对于任意的有向边(u, v),u在拓扑序列中都出现在v之前。
拓扑排序可以用来解决一些实际问题,比如任务调度、编译顺序等。在一个任务调度的问题中,每个顶点表示一个任务,有向边(u, v)表示任务u必须在任务v之前执行。拓扑序列可以用来确定任务的执行顺序,保证所有的依赖关系都得到满足。
拓扑序列可能不是唯一的,一个图可以有多个拓扑序列。可以使用深度优先搜索(DFS)或广度优先搜索(BFS)等算法来生成拓扑序列。
拓扑序列的生成过程如下:
- 选择一个没有前驱(即入度为0)的顶点,将其加入拓扑序列中。
- 移除该顶点及其相邻的边。
- 重复步骤1和2,直到所有的顶点都加入了拓扑序列。
如果图中存在环路,则无法生成拓扑序列,因为环路表示存在循环依赖关系,无法确定任务的执行顺序。
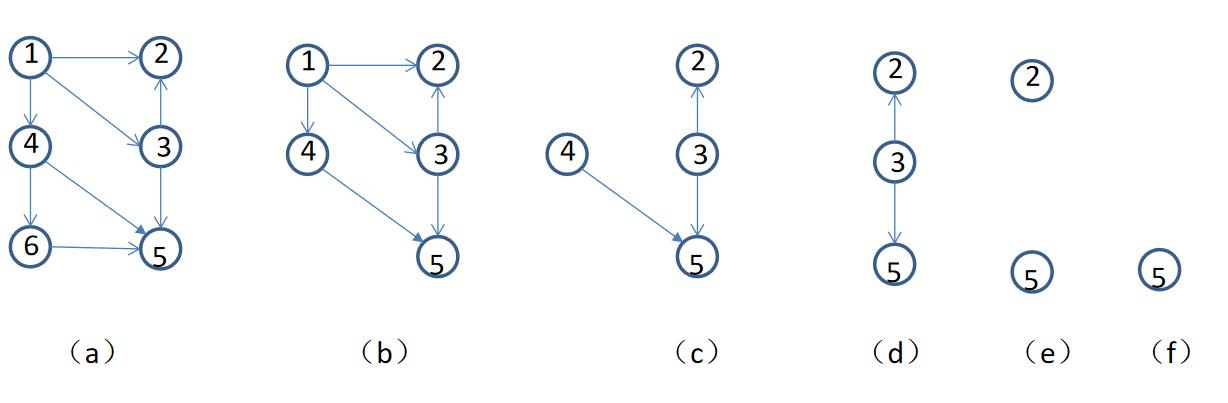
将有向图的有向边作为活动开始的顺序,若图中一个节点入度为0,则应该最先执行此活动,而后删除掉此节点和其关联的有向边,再去找图中其他没有入度的结点,执行活动,依次进行,示例如下:
🚀感谢:给读者的一封信
亲爱的读者,
我在这篇文章中投入了大量的心血和时间,希望为您提供有价值的内容。这篇文章包含了深入的研究和个人经验,我相信这些信息对您非常有帮助。
如果您觉得这篇文章对您有所帮助,我诚恳地请求您考虑赞赏1元钱的支持。这个金额不会对您的财务状况造成负担,但它会对我继续创作高质量的内容产生积极的影响。
我之所以写这篇文章,是因为我热爱分享有用的知识和见解。您的支持将帮助我继续这个使命,也鼓励我花更多的时间和精力创作更多有价值的内容。
如果您愿意支持我的创作,请扫描下面二维码,您的支持将不胜感激。同时,如果您有任何反馈或建议,也欢迎与我分享。

再次感谢您的阅读和支持!
最诚挚的问候, “愚公搬代码”
- 点赞
- 收藏
- 关注作者


评论(0)