布隆过滤器的应用和原理
前言
不知道大家在面试时有没有被问过“如何在大量数据中快速检测某个数据是否存在”。如果有过相关的思考和解决方案,看看你的方案是否和本文一样。如果还没有,那希望看了本文后可以给你提供一些启发和帮助,以备之后的使用和面试。
问题剖析
通常我们查找某个数据是否存在需要借助一些集合,比如数组、列表、哈希表、树等,其中哈希表相对其他集合的查找速度较快,但是这里有个重点“大量数据”,比如“在13亿个人的集合中查找某个人是否存在”,如果就使用哈希表来存储,我们先来看下空间代价:
以 Java 为例,假设哈希表的 key 为 String 类型,中文3个字占用9个字节,value 为 null 占用空间先忽略。这样下来一条记录占9个字节,考虑13亿人名字重复,就按照10亿算,那么就是90亿字节,粗略算下来也得8GB。
可能有些人会认为8G还好,那100亿条数据呢?1000亿呢?这种方式显然不是最优解。有没有一种方法可以节省空间?答案是有的,那就是布隆过滤器,下面对此进行介绍。
布隆过滤器
介绍
布隆过滤器是1970年一个叫布隆的人提出来的,主要用于检测一个元素是否在一个集合里。其空间效率和查询时间都远远超过一般的算法,但是会存在一定的失误率,下面对其进行详细说明。
原理
布隆过滤器原理就是位图加哈希,这里先了解下位图和哈希函数。
- 位图就是一个二进制位数组,其基本思想是用一个二进制位就可以表示一个元素,如果要存储大量的数据,通过位图可以大大节省空间。比如一个4字节的int类型的数据在位图中表示的话只需要占用1bit。
- 哈希函数可以将任意长度的输入输出到一个有限的输出域中,具有相同输入相同输出、离散性等特征。通过哈希函数后可以快速定位元素所在位置。
使用布隆过滤器添加或者查找元素,就是将元素通过一组哈希函数映射到位图中,不论该元素多大都只需要占用1位,从而节省大量空间,如下图添加一个元素:
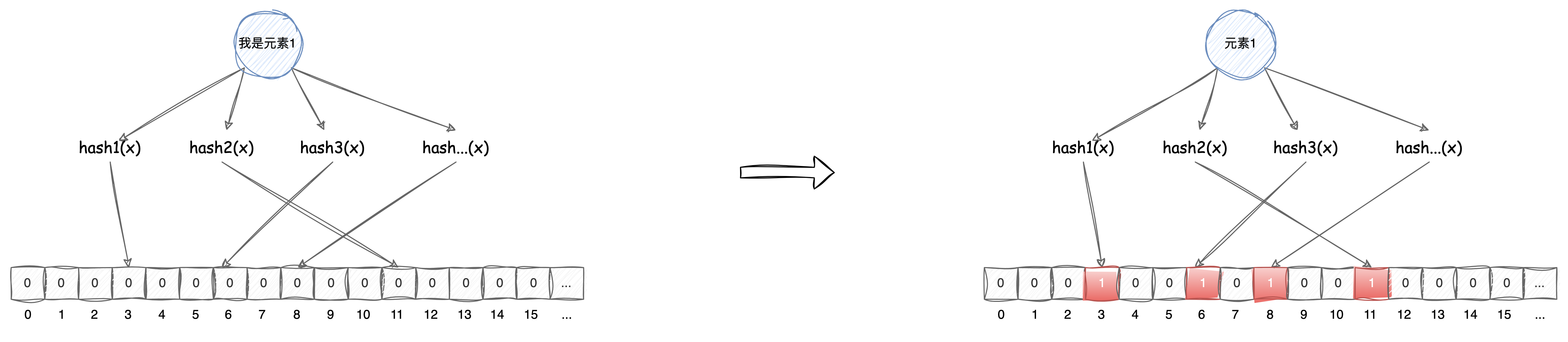
元素1分别通过hash1、hash2、hash3、hash…等多个哈希函数后,每个函数对应的输出值会分别映射到位图的下标,并将该下标值设置为1,以此说明该元素在这个位置上。
这样算下来,上面所说的10亿人可以占10亿位,抛开其他因素,占用空间只有0.1G左右,可见空间的节省程度。(如果有对哈希函数个数有疑问的,请继续向下看)
同样,查找该元素时以同样的方式进行查找,通过哈希函数映射到数组中,如果下标对应的值为1,说明该元素存在。但是,查找时会有失误率,先看图
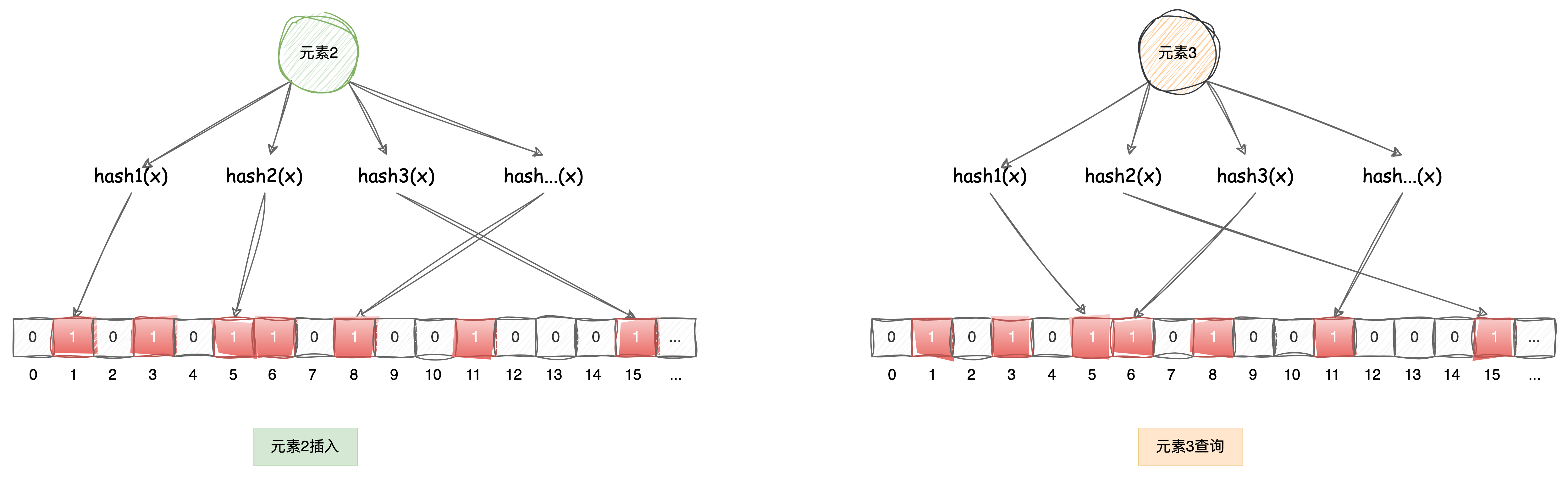
当元素2插入后位图的状态如图左,此后,如果检测元素3存不存在位图中(元素3在此之前并没有添加进来),因为哈希存在冲突问题,所以可能会出现图右的情况,这就是查找失误了。当然,这只是个别情况,大多情况如下图
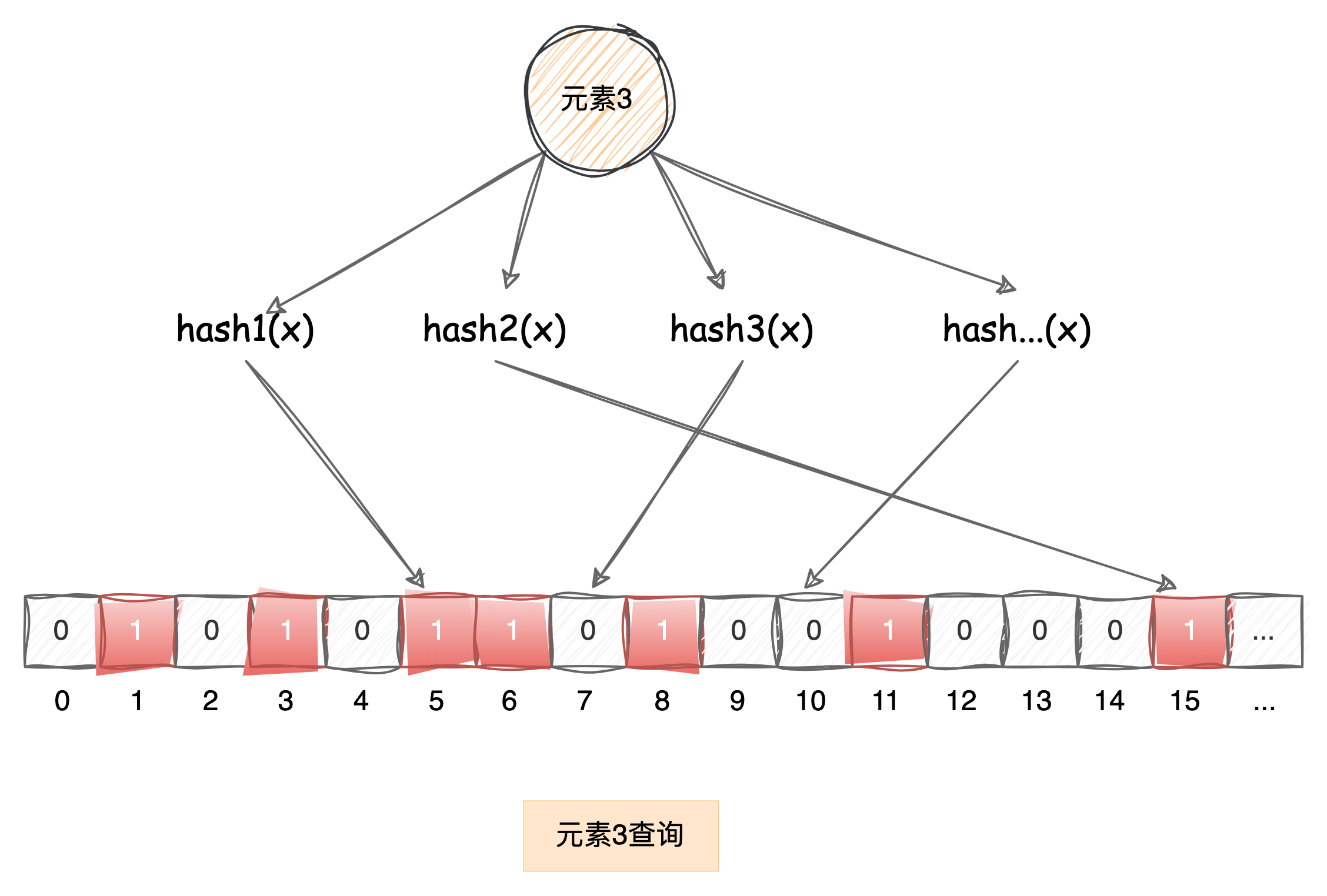
大多情况只有个别哈希函数冲突,只要有一个下标对应的值为0,该元素也被视为不存在。这也是为什么有多个哈希函数的原因,为了降低因哈希冲突产生的查找失误。
这里重点强调一下:失误率是指查找不存在的元素会有该现象,在位图中存在的元素不会出现查找失误。
影响失误率的因素
那是不是哈希函数个数越多失误率越低,当然不是。就如下图,当位图长度和哈希函数个数都为4时,任意一个元素来都能找到,这失误率就太大了。
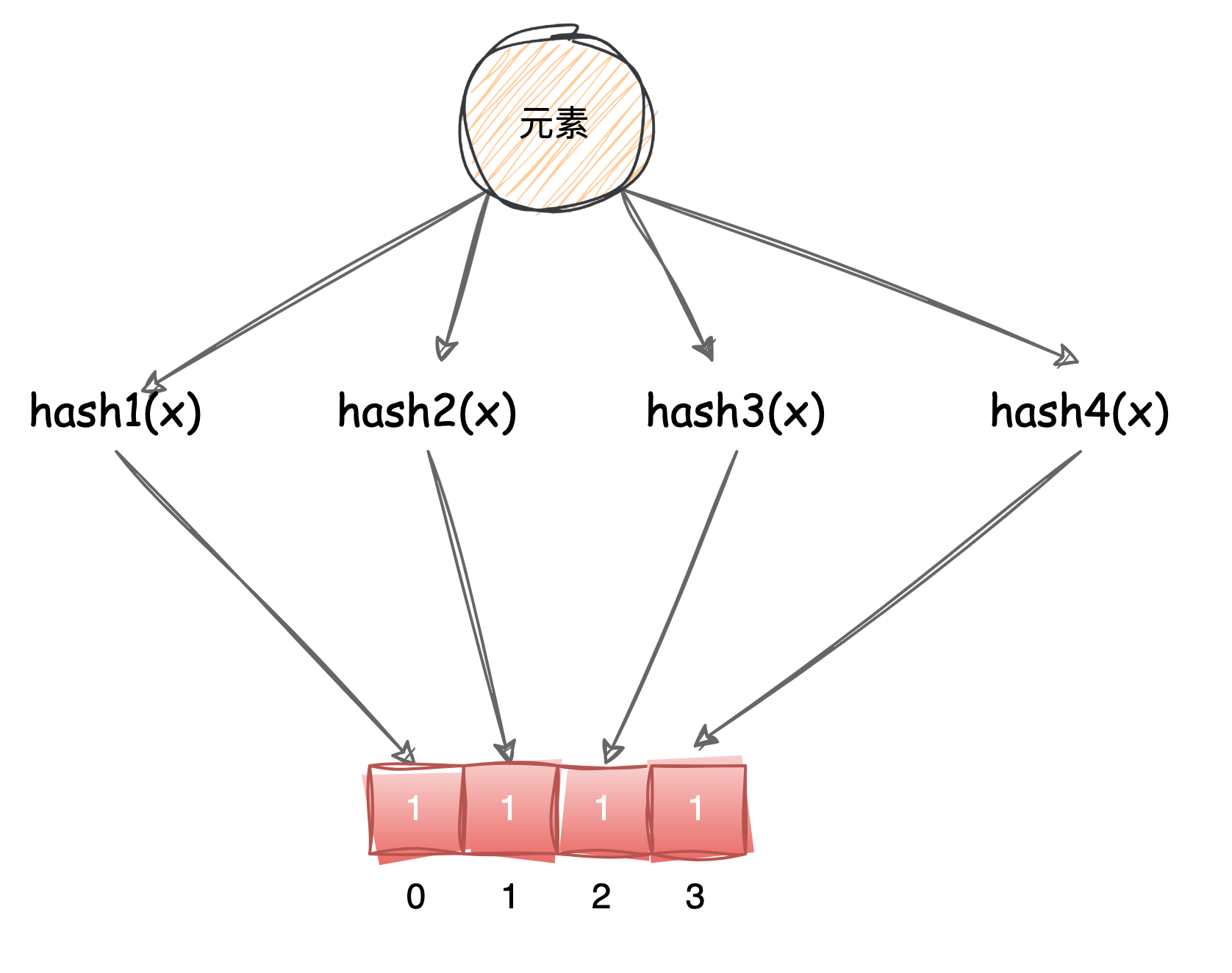
所以失误率与位图的长度还有哈希函数的个数都是有关系的。
-
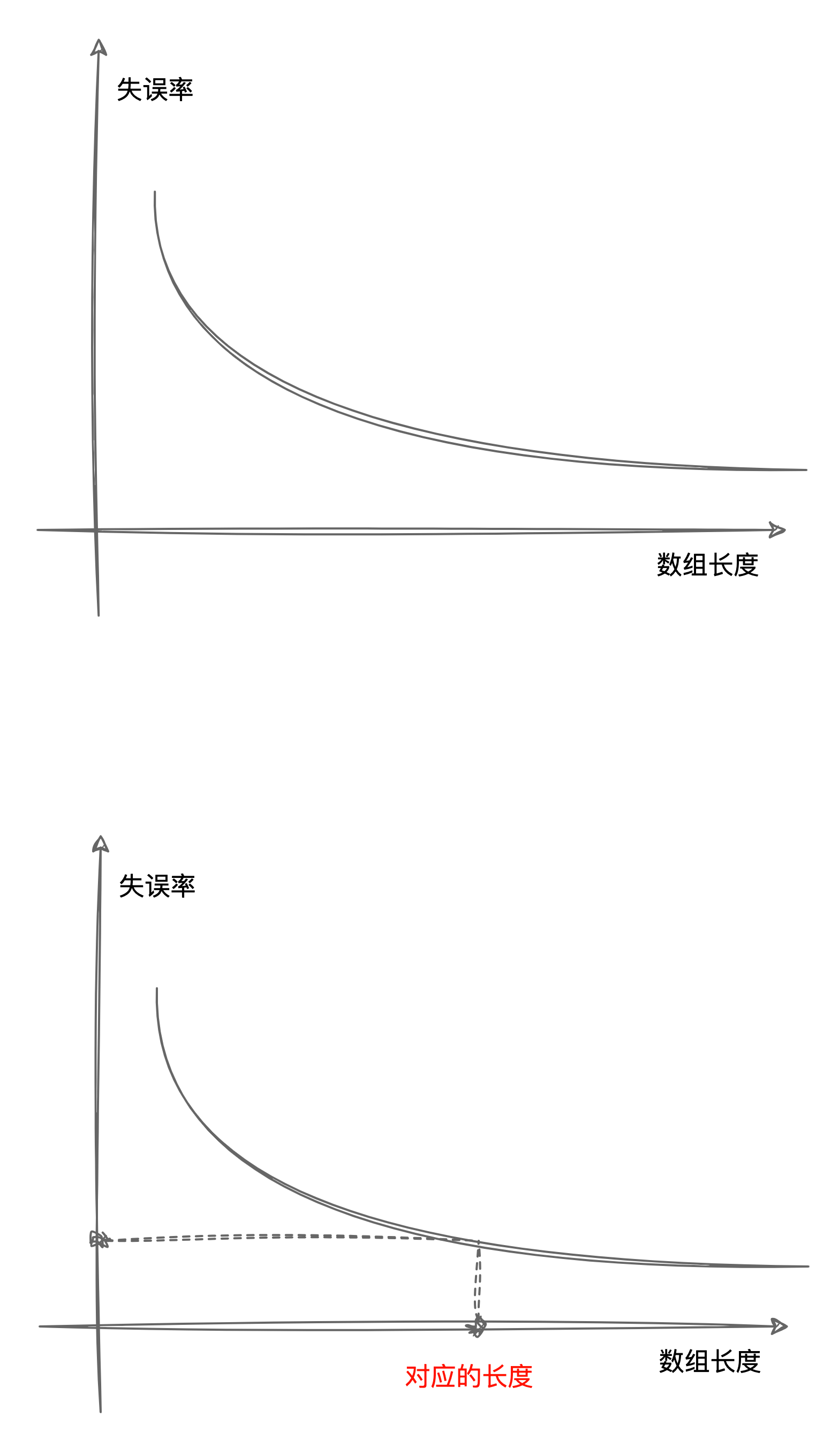
和位图长度的关系:在数据量固定的情况下,位图长度越大,失误率越低。所以长度怎么定?找到能接受的失误率,其所对应的长度就行。如下图

这里给出求数组长度的公式:$$ \ m = \ - \frac{n*ln§ }{ (ln(2))^2} $$
其中m为数组长度,n是数据量,p是给定的失误率。 -
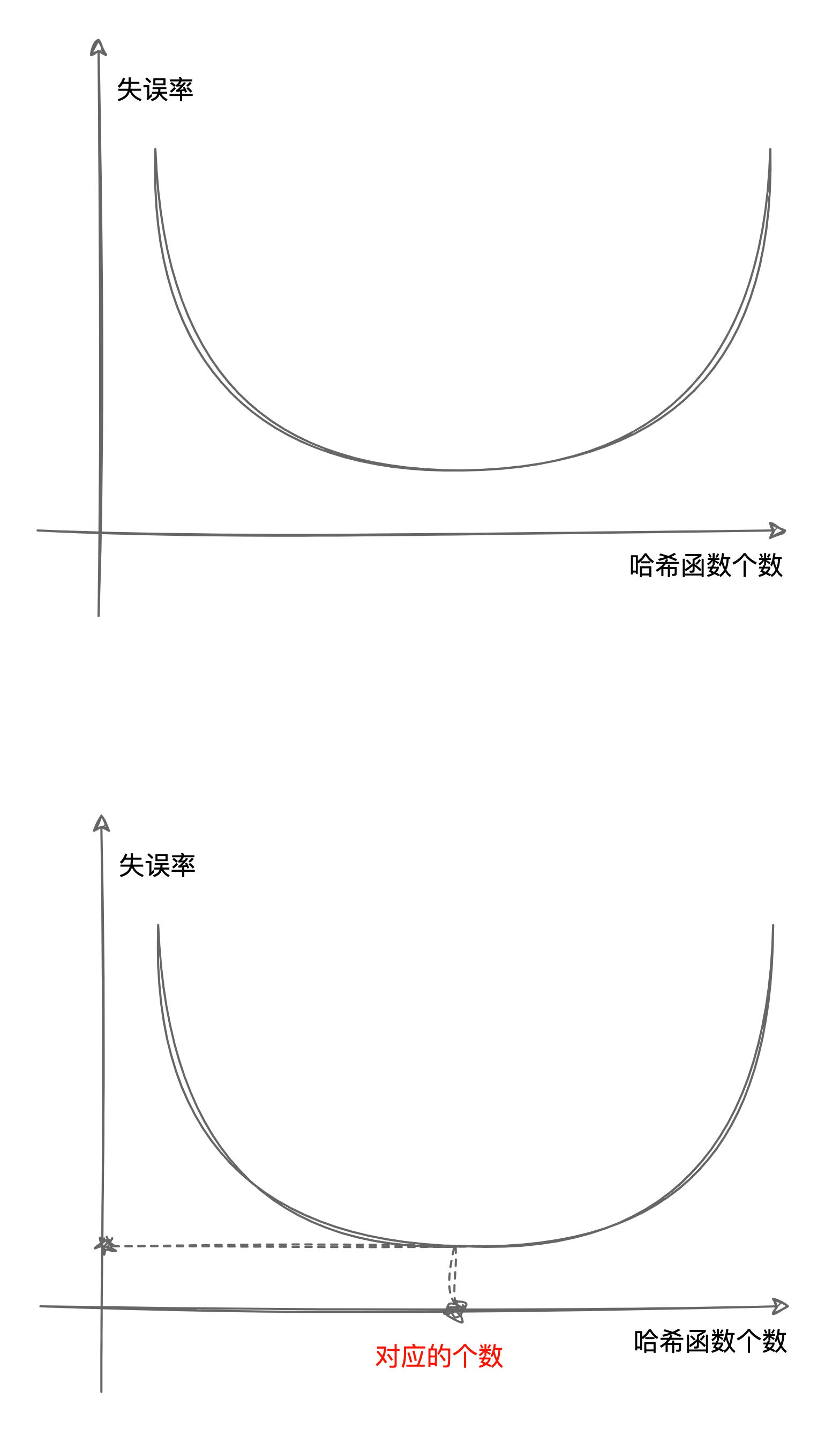
和哈希函数个数的关系:哈希函数个数少了会因为冲突提高失误率,多了也会因为大量数据占用位图导致失误率的提高。所以哈希函数个数怎么定?找到失误率最低对应的函数个数。如下图

这里给出求哈希函数个数的公式:$$ \ k = \frac{m }{ n} * ln(2)$$
其中k为哈希函数个数,n是数据量,m是位图数组长度。
通常数组长度和哈希函数个数求出来后需要向上或向下取整,这样的话真实的失误率与预定的失误率极就不相等的,此时就需要求出真实的失误率,然后根据实际起ing狂进行调整。
这里给出求真实失误率的公式:$$ \ p =(1 - e^ {-\frac{nk }{ m}} )^k$$
其中p为真实失误率,n是数据量,k是哈希函数个数,m是位图数组长度。
总结
在这个数据大爆炸的时代,布隆过滤器适用于大量的场景,比如redis的缓存穿透怎么处理、垃圾邮件过滤、数据去重等。而且布隆过滤器已经有大量的实现,比如redis就支持了该数据类型,还有Google的Guava库也有具体的实现,所以可以直接站在巨人的肩膀上解决问题。不过还是那句话,我们要知其然知其所以然。
- 点赞
- 收藏
- 关注作者


评论(0)