【愚公系列】2023年12月 WEBGL专题-图形旋转矩阵
🏆 作者简介,愚公搬代码
🏆《头衔》:华为云特约编辑,华为云云享专家,华为开发者专家,华为产品云测专家,CSDN博客专家,CSDN商业化专家,阿里云专家博主,阿里云签约作者,腾讯云优秀博主,腾讯云内容共创官,掘金优秀博主,51CTO博客专家等。
🏆《近期荣誉》:2023年华为云十佳博主,2022年CSDN博客之星TOP2,2022年华为云十佳博主等。
🏆《博客内容》:.NET、Java、Python、Go、Node、前端、IOS、Android、鸿蒙、Linux、物联网、网络安全、大数据、人工智能、U3D游戏、小程序等相关领域知识。
🏆🎉欢迎 👍点赞✍评论⭐收藏
🚀前言
图形平移、缩放、旋转是计算机图形学中常用的操作,用来改变图像的位置、大小和方向。
-
平移:平移是将图形在二维平面上沿着一个方向移动一段距离,通常用一个二维向量表示平移的距离。在计算机图形学中,可以通过修改坐标系来实现平移操作。
-
缩放:缩放是将图形按照一定比例进行放大或缩小,在计算机图形学中,通常使用缩放矩阵来进行缩放操作。缩放矩阵中,对角线上的元素表示沿着坐标轴的缩放比例,非对角线上的元素表示斜线方向的缩放比例。
-
旋转:旋转是将图形围绕某个点或轴旋转一定角度,通常使用旋转矩阵来实现。旋转矩阵是一个二维矩阵,其中cos和sin分别表示旋转角度的余弦和正弦值。通过对图形中每个点进行旋转矩阵变换,可以实现旋转操作。
这些操作常常用于计算机图形学、图像处理等领域中的图像变换。图形平移、缩放、旋转是计算机图形学中常用的操作,用来改变图像的位置、大小和方向。
🚀一、图形平移矩阵
🔎1.矩阵的概念
矩阵是一个数学对象,由一组数排成的矩形排列组成。它可看作向量的扩展。通常表示为一个大写字母,如A、B等,其中每一个元素都用小写字母表示。一个矩阵包含了一定数量的行和列,并且每个元素都可以在矩阵中通过其行号和列号来确定其位置。
一般地,一个m×n矩阵A的元素可以表示为a[i,j],其中i表示该元素所在的行数,j表示该元素所在的列数。例如,对于一个3×3的矩阵A,其元素可以表示为:
A = [ a[1,1] a[1,2] a[1,3] ]
[ a[2,1] a[2,2] a[2,3] ]
[ a[3,1] a[3,2] a[3,3] ]
矩阵广泛应用于线性代数、图论、概率论等许多数学分支领域,以及计算机科学、物理、经济学、工程学等其他学科中。
矩阵就是纵横排列的数据表格(m行n列),作用是把一个点转换到另一个点。
🔎2.行主序和列主序
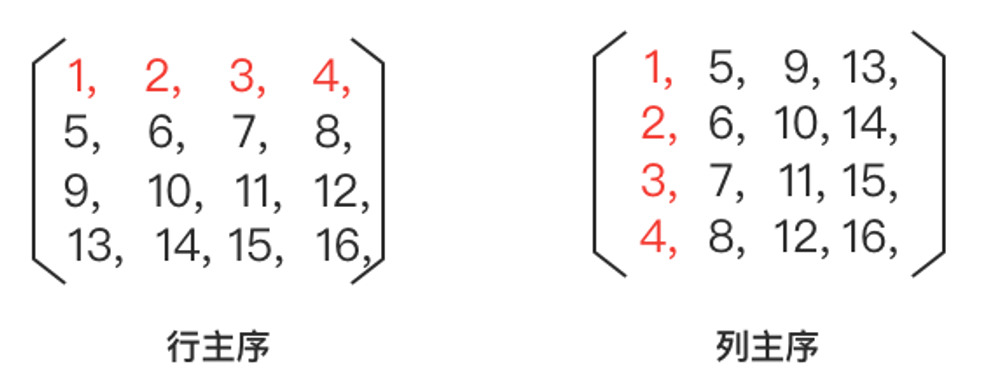
矩阵的行主序和列主序都是指存储顺序。
行主序指矩阵元素按行依次存储的方式,即先存储第一行的元素,再存储第二行的元素,以此类推,直到最后一行的元素。在计算机中,矩阵的行主序存储方式是一般的存储方式。
列主序指矩阵元素按列依次存储的方式,即先存储第一列的元素,再存储第二列的元素,以此类推,直到最后一列的元素。在计算机中,矩阵的列主序存储方式也常用于某些特定的应用场景,例如矩阵乘法算法的优化。
🔎3.三维坐标矩阵

🔎4.旋转矩阵
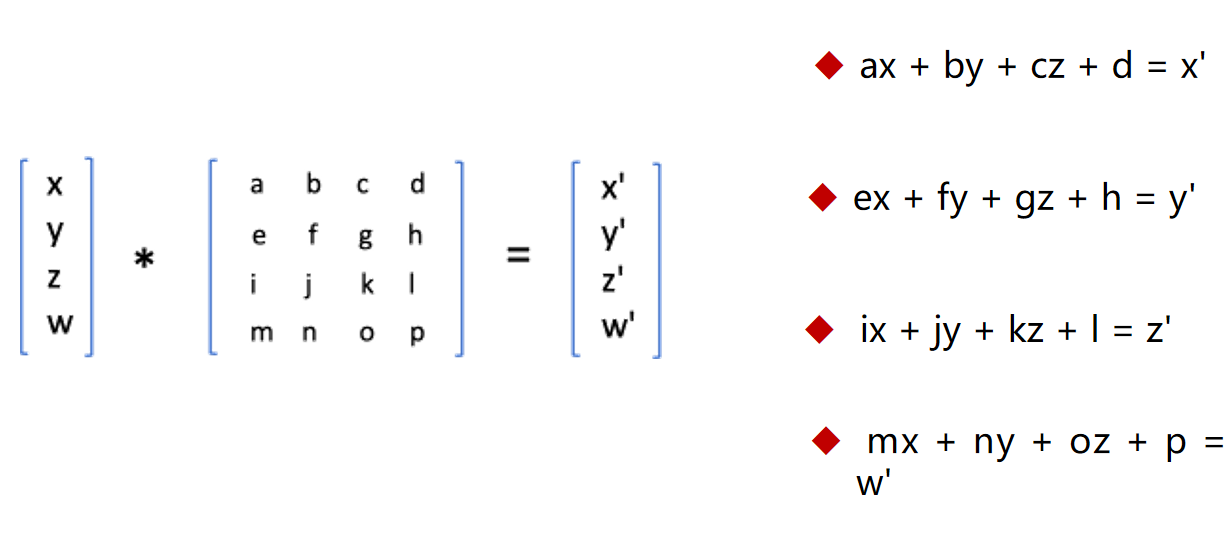
1、ax + by + cz + w = x * cos(β) - y * sin(β) :
只有当 a = cos(β),b = -sin(β), c = w = 0 的时候,等式左右两边成立
2、ex + fy + gz + h = y * cos(β) + x * sin(β) :
只有当 e = sin(β) f = cos(β), g = h = 0 的时候,等式左右两边成立
3、ix + jy + kz + l = z’ :
只有当 k = 1, i = j = k = 0 的时候,等式左右两边成立
4、mx + ny + oz + p = 1’ :
只有当 m = n = o = 0, p = 1 的时候,等式左右两边成立

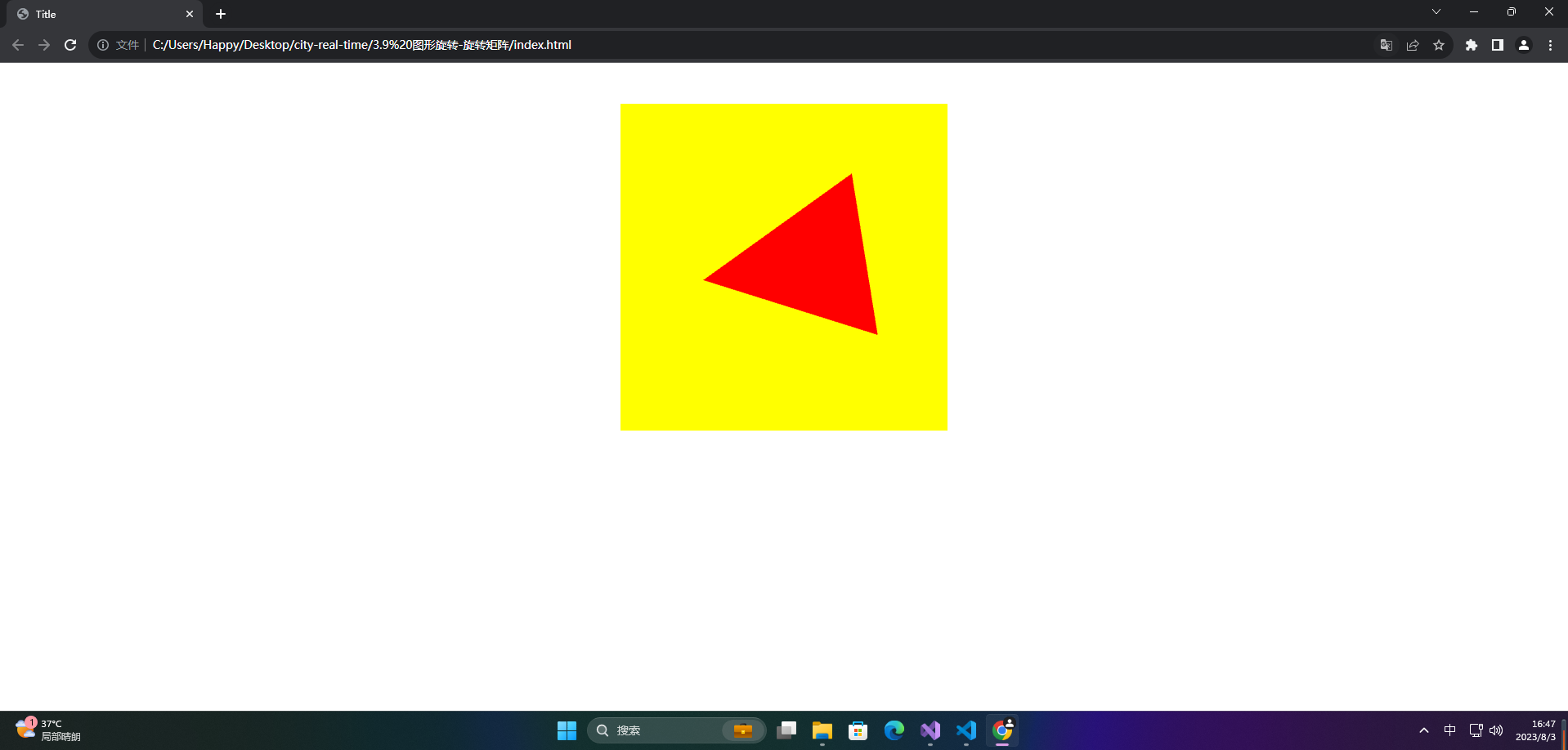
🔎5.案例
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>Title</title>
<script src="../lib/index.js"></script>
<style>
* {
margin: 0;
padding: 0;
}
canvas{
margin: 50px auto 0;
display: block;
background: yellow;
}
</style>
</head>
<body>
<canvas id="canvas" width="400" height="400">
此浏览器不支持canvas
</canvas>
</body>
</html>
<script>
// 绕z轴旋转的旋转矩阵
function getRotateMatrix(deg) {
return new Float32Array([
Math.cos(deg) ,Math.sin(deg) ,0.0,0.0,
-Math.sin(deg) ,Math.cos(deg) ,0.0,0.0,
0.0, 0.0, 1.0,0.0,
0.0, 0.0, 0.0, 1,
])
}
const ctx = document.getElementById('canvas')
const gl = ctx.getContext('webgl')
// 创建着色器源码
const VERTEX_SHADER_SOURCE = `
attribute vec4 aPosition;
uniform mat4 mat;
void main() {
gl_Position = mat * aPosition;
gl_PointSize = 10.0;
}
`; // 顶点着色器
const FRAGMENT_SHADER_SOURCE = `
void main() {
gl_FragColor = vec4(1.0,0.0,0.0,1.0);
}
`; // 片元着色器
const program = initShader(gl, VERTEX_SHADER_SOURCE, FRAGMENT_SHADER_SOURCE)
const aPosition = gl.getAttribLocation(program, 'aPosition');
const mat = gl.getUniformLocation(program, 'mat');
const points = new Float32Array([
-0.5, -0.5,
0.5, -0.5,
0.0, 0.5,
])
const buffer = gl.createBuffer();
gl.bindBuffer(gl.ARRAY_BUFFER, buffer);
gl.bufferData(gl.ARRAY_BUFFER, points, gl.STATIC_DRAW);
gl.vertexAttribPointer(aPosition, 2, gl.FLOAT, false, 0, 0);
gl.enableVertexAttribArray(aPosition)
let x = 0;
function animation() {
x += 0.01;
const matrix = getRotateMatrix(x);
// gl.vertexAttrib1f(aTranslate, x);
gl.uniformMatrix4fv(mat, false, matrix);
gl.drawArrays(gl.TRIANGLES, 0, 3);
requestAnimationFrame(animation);
}
animation()
</script>
🚀感谢:给读者的一封信
亲爱的读者,
我在这篇文章中投入了大量的心血和时间,希望为您提供有价值的内容。这篇文章包含了深入的研究和个人经验,我相信这些信息对您非常有帮助。
如果您觉得这篇文章对您有所帮助,我诚恳地请求您考虑赞赏1元钱的支持。这个金额不会对您的财务状况造成负担,但它会对我继续创作高质量的内容产生积极的影响。
我之所以写这篇文章,是因为我热爱分享有用的知识和见解。您的支持将帮助我继续这个使命,也鼓励我花更多的时间和精力创作更多有价值的内容。
如果您愿意支持我的创作,请扫描下面二维码,您的支持将不胜感激。同时,如果您有任何反馈或建议,也欢迎与我分享。

再次感谢您的阅读和支持!
最诚挚的问候, “愚公搬代码”
- 点赞
- 收藏
- 关注作者


评论(0)