【愚公系列】2023年12月 五大常用算法(四)-贪心算法
🏆 作者简介,愚公搬代码
🏆《头衔》:华为云特约编辑,华为云云享专家,华为开发者专家,华为产品云测专家,CSDN博客专家,阿里云专家博主,腾讯云优秀博主,掘金优秀博主,51CTO博客专家等。
🏆《近期荣誉》:2022年CSDN博客之星TOP2,2022年华为云十佳博主等。
🏆《博客内容》:.NET、Java、Python、Go、Node、前端、IOS、Android、鸿蒙、Linux、物联网、网络安全、大数据、人工智能、U3D游戏、小程序等相关领域知识。
🏆🎉欢迎 👍点赞✍评论⭐收藏
🚀前言
五大常用算法的特点如下:
-
分治:将一个大问题拆分成若干个小问题,分别解决,然后将解决结果合并起来得到整个问题的解。分治算法的特点是递归,效率高,但对数据的规律要求比较高,需要较高的算法设计技巧。常见应用领域为排序、查找和统计等。
-
动态规划:将一个大问题分解成若干个小问题,通过寻找子问题之间的递推关系,求解小问题的最优解,然后将小问题的最优解组合起来解决整个大问题。动态规划的特点是可以解决具有重叠子问题的问题,但需要较高的时间和空间复杂度。常见应用领域为求解最大子序列、背包问题等。
-
贪心:在处理问题的过程中,每次做出局部最优的选择,希望通过局部最优的选择达到全局最优。贪心算法的特点是快速、简单,但是无法保证每个局部最优解会导致全局最优解。常见应用领域为最小生成树、活动安排等。
-
回溯:通过不断尝试局部的解,如果不满足要求就回溯返回,直到找到解为止。回溯算法的特点是可以解决多种类型的问题,但需要搜索所有可能的解,时间复杂度较高。常见应用领域为八皇后问题、排列组合问题等。
-
分支限界:与回溯算法相似,但是在搜索的过程中,通过剪枝操作来减少搜索的空间,提高算法效率。常见应用领域为旅行商问题、图着色问题等。
🚀一、贪心算法
🔎1.基本思想
贪心算法(Greedy Algorithm)的基本思想是,在每一步中都选择局部最优的解,最终得到全局最优解。也就是说,贪心算法是在一定的约束条件下,逐步地构建问题的解,通过每一步选择局部最优的策略来达到全局最优的解。贪心算法的求解过程非常高效,但有时可能会得到次优解或者无解。因此,在应用贪心算法时,需要注意问题的约束条件和性质,以及选取合适的贪心策略。
/**
* File: coin_change_greedy.cs
* Created Time: 2023-07-21
* Author: hpstory (hpstory1024@163.com)
*/
namespace hello_algo.chapter_greedy;
public class coin_change_greedy {
/* 零钱兑换:贪心 */
public int coinChangeGreedy(int[] coins, int amt) {
// 假设 coins 列表有序
int i = coins.Length - 1;
int count = 0;
// 循环进行贪心选择,直到无剩余金额
while (amt > 0) {
// 找到小于且最接近剩余金额的硬币
while (i > 0 && coins[i] > amt) {
i--;
}
// 选择 coins[i]
amt -= coins[i];
count++;
}
// 若未找到可行方案,则返回 -1
return amt == 0 ? count : -1;
}
[Test]
public void Test() {
// 贪心:能够保证找到全局最优解
int[] coins = { 1, 5, 10, 20, 50, 100 };
int amt = 186;
int res = coinChangeGreedy(coins, amt);
Console.WriteLine("\ncoins = " + coins.PrintList() + ", amt = " + amt);
Console.WriteLine("凑到 " + amt + " 所需的最少硬币数量为 " + res);
// 贪心:无法保证找到全局最优解
coins = new int[] { 1, 20, 50 };
amt = 60;
res = coinChangeGreedy(coins, amt);
Console.WriteLine("\ncoins = " + coins.PrintList() + ", amt = " + amt);
Console.WriteLine("凑到 " + amt + " 所需的最少硬币数量为 " + res);
Console.WriteLine("实际上需要的最少数量为 3 ,即 20 + 20 + 20");
// 贪心:无法保证找到全局最优解
coins = new int[] { 1, 49, 50 };
amt = 98;
res = coinChangeGreedy(coins, amt);
Console.WriteLine("\ncoins = " + coins.PrintList() + ", amt = " + amt);
Console.WriteLine("凑到 " + amt + " 所需的最少硬币数量为 " + res);
Console.WriteLine("实际上需要的最少数量为 2 ,即 49 + 49");
}
}

🦋1.1 贪心优点与局限性
贪心算法的优点:
- 算法执行效率高,因为贪心算法通常只需要做出局部最优解,而不必考虑全局最优解。
- 实现简单,易于理解和编写。
- 贪心算法常常被用作其他算法的优化和辅助算法。
贪心算法的局限性:
- 贪心算法得出的解不一定是全局最优解,因为贪心算法只考虑每一步的最优解,并没有考虑到全局的影响。
- 贪心算法要求问题具有最优子结构性质,即问题的最优解包含子问题的最优解,但并不是所有问题都具有最优子结构性质。
- 贪心算法对于涉及到连续区间的问题通常不适用,因为贪心算法无法保证局部最优解一定能得到全局最优解。

🦋1.2 贪心算法特性
贪心算法是一种基于贪心思想的算法,其特点如下:
-
贪心选择性质:贪心算法通过每一步的贪心选择,得到全局最优解。
-
最优子结构性质:问题的最优解包含其子问题的最优解。
-
无后效性:当应用贪心策略时,只考虑当前状态,不考虑以后的决策,即前面的选择决定后面的选择。
-
可行解性:贪心算法得到的解必须是问题的可行解。
-
不一定总是能得到全局最优解:有些问题即使满足贪心选择性质、最优子结构性质和无后效性,也不能保证贪心算法能得到全局最优解。
🦋1.3 贪心解题步骤
贪心算法一般有以下解题步骤:
-
确定问题的优化目标,将问题转化为求解最大值或最小值的问题。
-
将问题的解空间按照某种策略划分成若干子问题的解空间。
-
选取一个贪心策略,即每次选取最优解的局部最优策略,并证明该策略是全局最优的。
-
将贪心策略递归地应用到每个子问题中,得到每个子问题的局部最优解,最终得到原问题的最优解。
-
检查是否满足问题的约束条件和最优化目标,并分析算法的时间复杂度和正确性。
贪心算法不一定能够求解所有问题,而是适用于一些特定的问题。因此,在应用贪心算法之前,需要进行问题分析,确定是否适用贪心算法。
🦋1.4 贪心典型例题
一些贪心算法的典型算法问题包括:
-
零钱兑换问题:给定一些不同面额的硬币和一个总金额,编写一个函数来计算可以凑成总金额的最少硬币数。
-
区间调度问题:给定一些区间,找到最多的互不重叠区间数。
-
最小生成树问题:给定一个无向加权图,找到一棵生成树使得所有边权的和最小。
-
背包问题:给定一些物品和一个背包,物品有不同的重量和价值,找到能放进背包的物品使得总价值最大。
-
最优矩阵链乘法问题:给定一组矩阵,找到一个最优的矩阵相乘顺序,使得计算乘积的次数最少。
这些问题都可以使用贪心算法来解决,通过不断地做出贪心的选择,最终得到全局最优解。
🔎2.分数背包问题
分数背包问题是指背包中物品可以被分割,部分装入背包。贪心算法可以用来解决分数背包问题。
具体步骤如下:
-
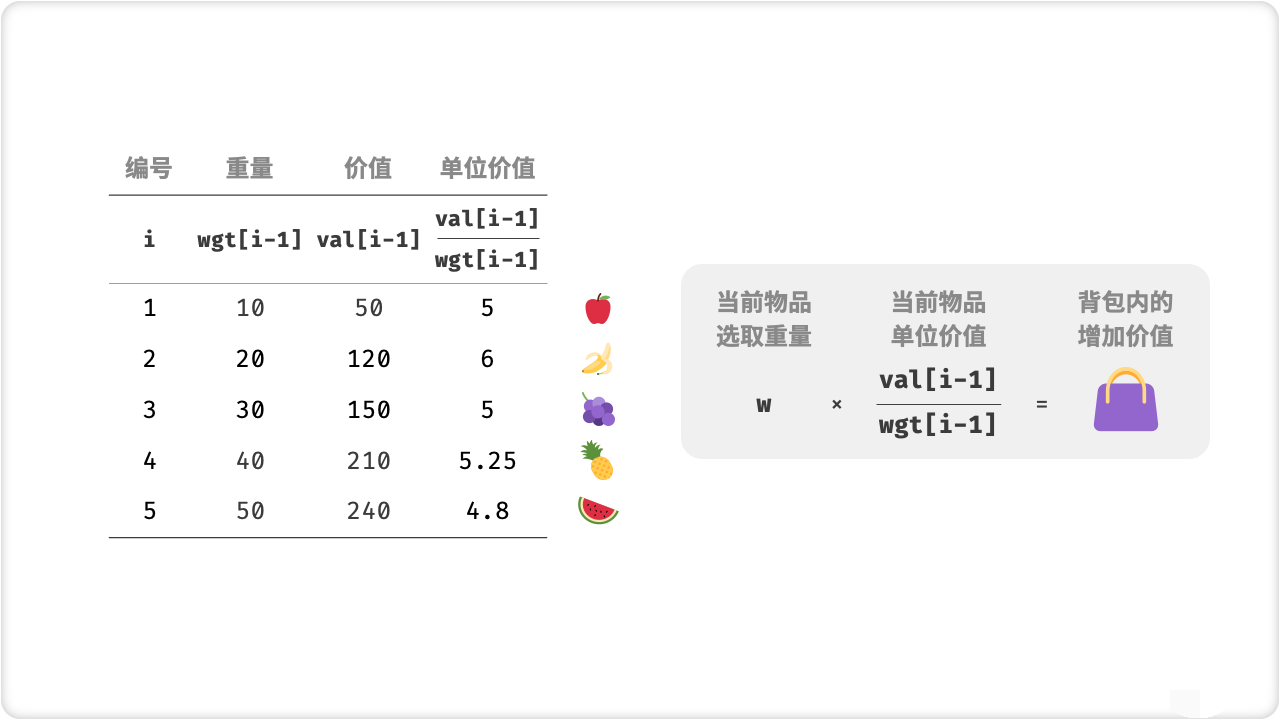
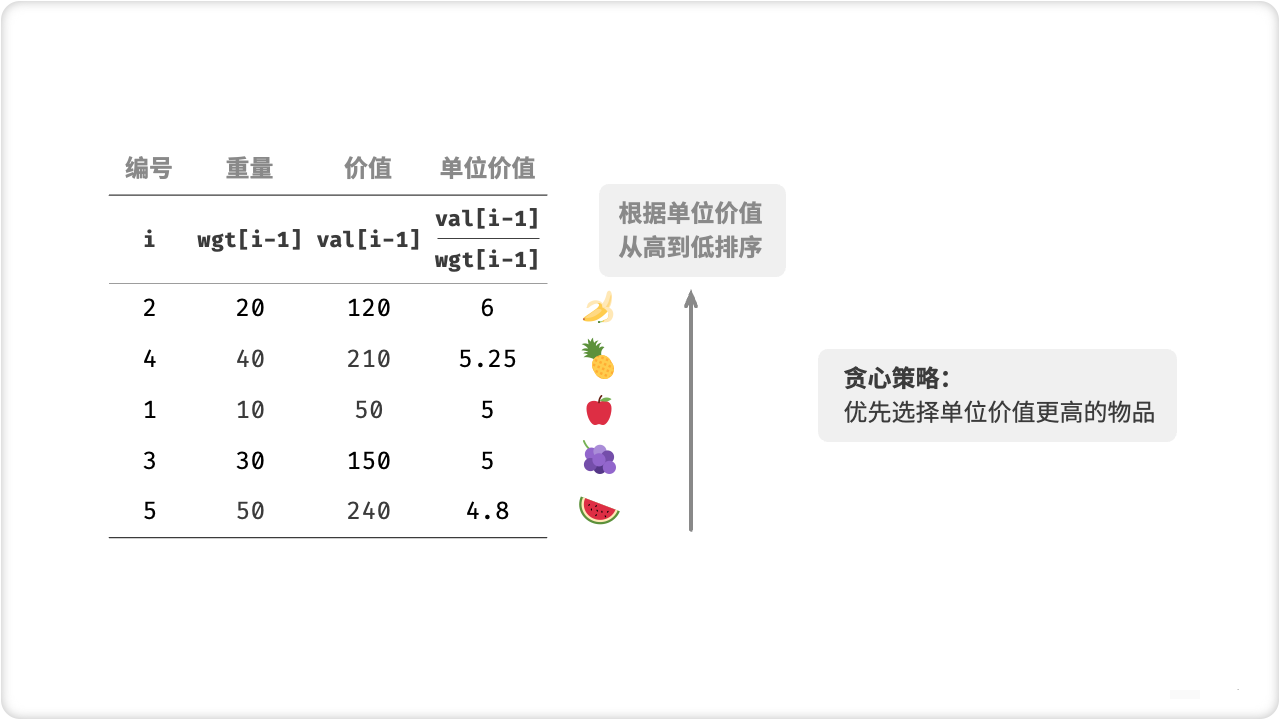
将所有物品按照性价比(价值/重量)从大到小排序。
-
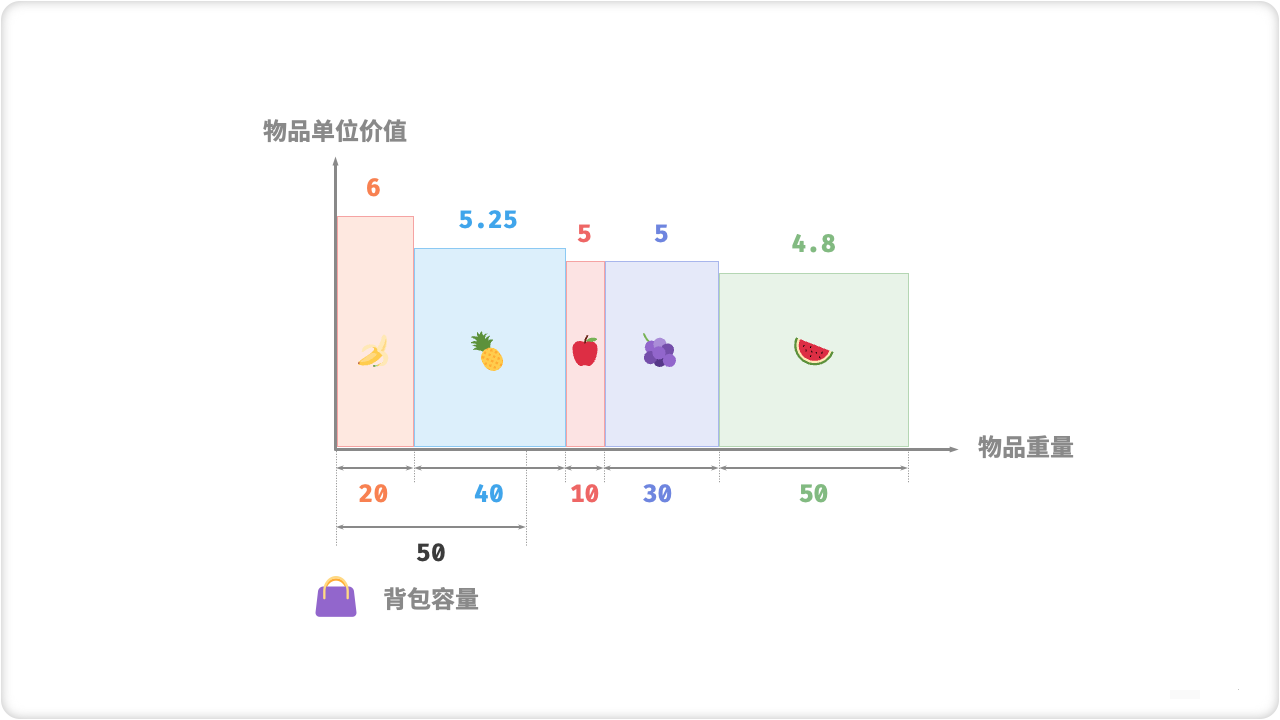
按照排序后的顺序,依次将物品放入背包:
(1)如果当前物品可以完全放入背包,就全部放入。
(2)如果当前物品不能完全放入背包,就将能放入的部分放入背包。
(3)如果当前物品无法放入任何部分,则不放入。
-
最终,背包中所有物品的总价值就是问题的最优解。
这种贪心策略的正确性在于,每次放入背包的物品都是当前剩余物品中性价比最高的,所以可以保证得到的解一定是最优的。

/* 物品 */
class Item {
public int w; // 物品重量
public int v; // 物品价值
public Item(int w, int v) {
this.w = w;
this.v = v;
}
}
public class fractional_knapsack {
/* 分数背包:贪心 */
public double fractionalKnapsack(int[] wgt, int[] val, int cap) {
// 创建物品列表,包含两个属性:重量、价值
Item[] items = new Item[wgt.Length];
for (int i = 0; i < wgt.Length; i++) {
items[i] = new Item(wgt[i], val[i]);
}
// 按照单位价值 item.v / item.w 从高到低进行排序
Array.Sort(items, (x, y) => (y.v / y.w).CompareTo(x.v / x.w));
// 循环贪心选择
double res = 0;
foreach (Item item in items) {
if (item.w <= cap) {
// 若剩余容量充足,则将当前物品整个装进背包
res += item.v;
cap -= item.w;
} else {
// 若剩余容量不足,则将当前物品的一部分装进背包
res += (double)item.v / item.w * cap;
// 已无剩余容量,因此跳出循环
break;
}
}
return res;
}
[Test]
public void Test() {
int[] wgt = { 10, 20, 30, 40, 50 };
int[] val = { 50, 120, 150, 210, 240 };
int cap = 50;
// 贪心算法
double res = fractionalKnapsack(wgt, val, cap);
Console.WriteLine("不超过背包容量的最大物品价值为 " + res);
}
}
🔎3.最大容量问题
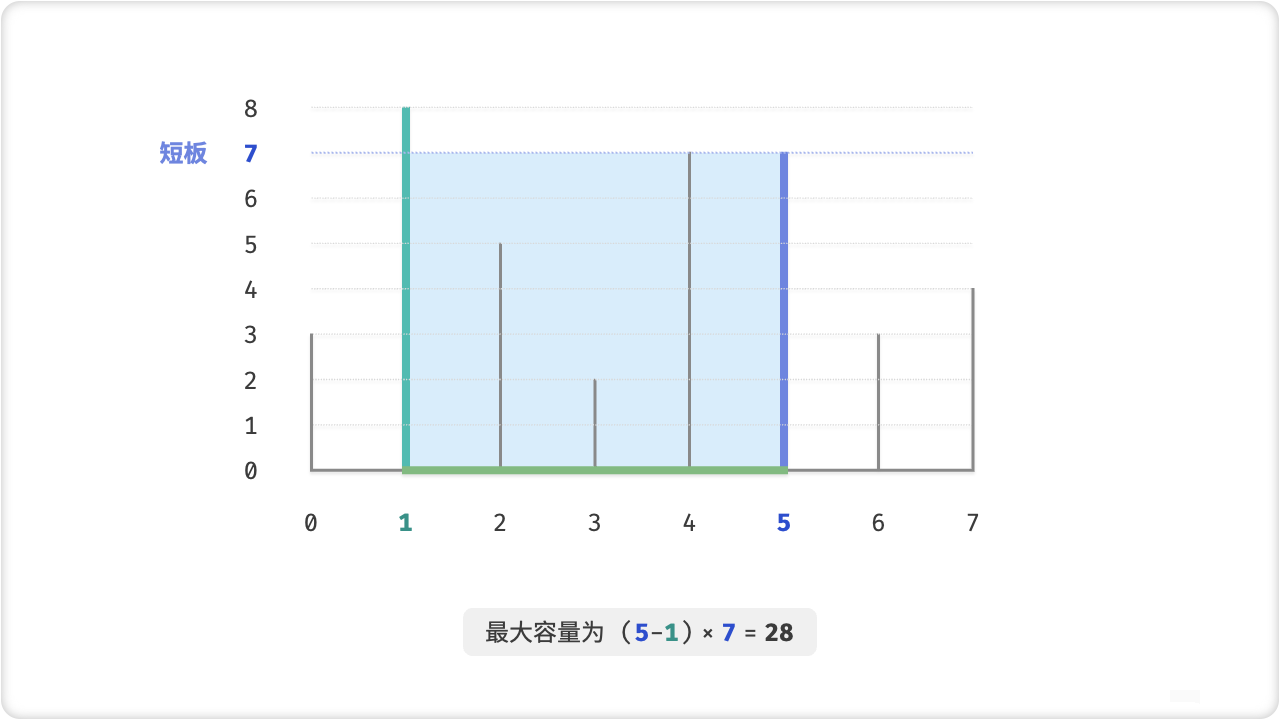
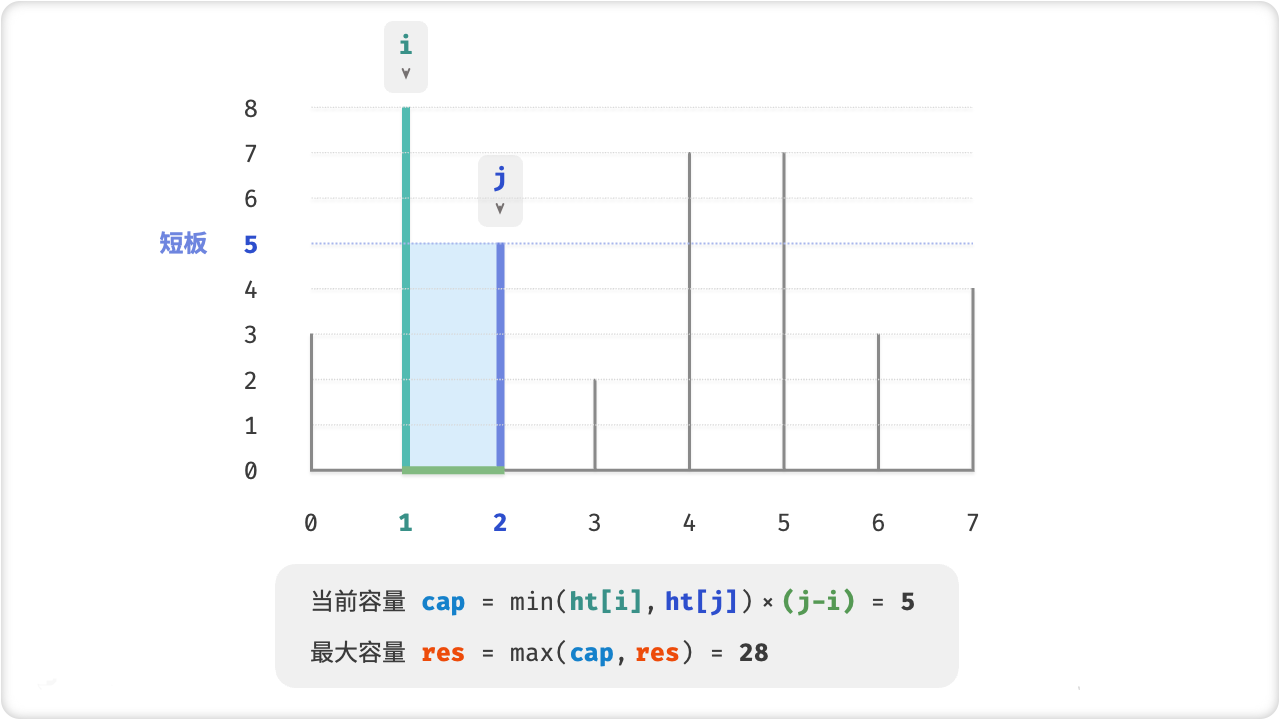
数组中的任意两个隔板,以及它们之间的空间可以组成一个容器。
容器的容量等于高度和宽度的乘积(即面积),其中高度由较短的隔板决定,宽度是两个隔板的数组索引之差。
请在数组中选择两个隔板,使得组成的容器的容量最大,返回最大容量。
public class max_capacity {
/* 最大容量:贪心 */
public int maxCapacity(int[] ht) {
// 初始化 i, j 分列数组两端
int i = 0, j = ht.Length - 1;
// 初始最大容量为 0
int res = 0;
// 循环贪心选择,直至两板相遇
while (i < j) {
// 更新最大容量
int cap = Math.Min(ht[i], ht[j]) * (j - i);
res = Math.Max(res, cap);
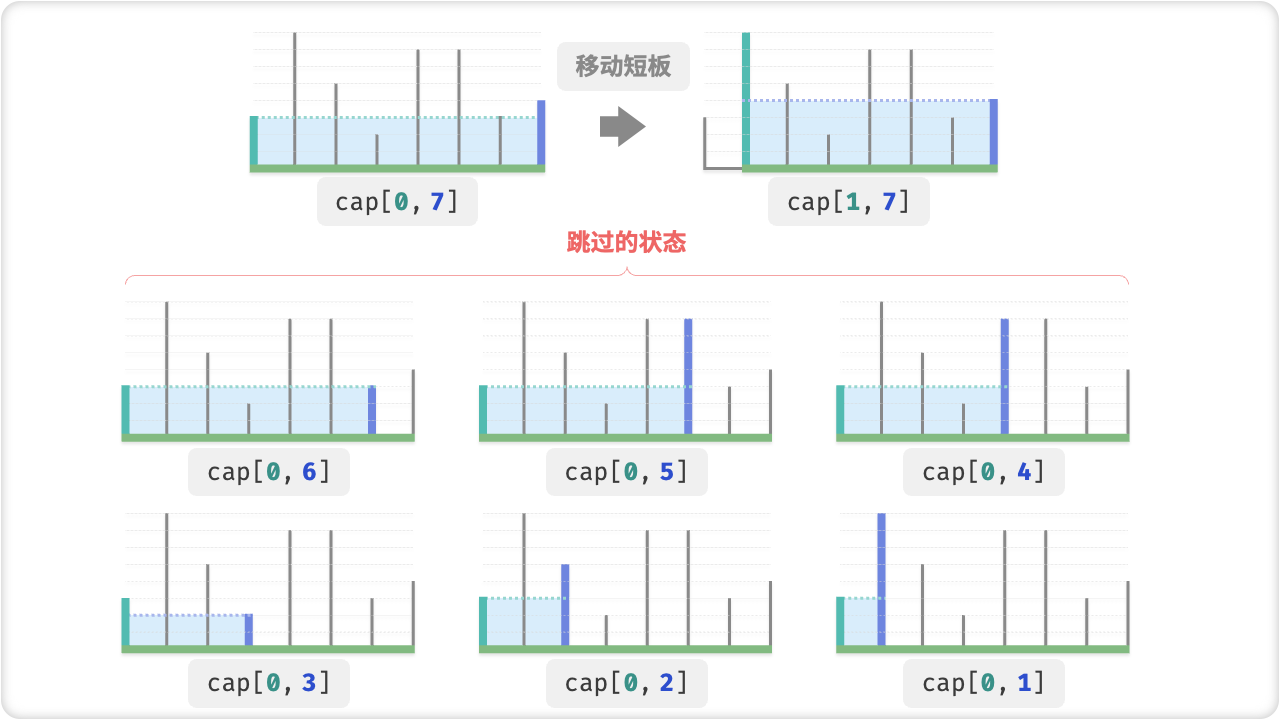
// 向内移动短板
if (ht[i] < ht[j]) {
i++;
} else {
j--;
}
}
return res;
}
[Test]
public void Test() {
int[] ht = { 3, 8, 5, 2, 7, 7, 3, 4 };
// 贪心算法
int res = maxCapacity(ht);
Console.WriteLine("最大容量为 " + res);
}
}
🔎4.最大切分乘积问题
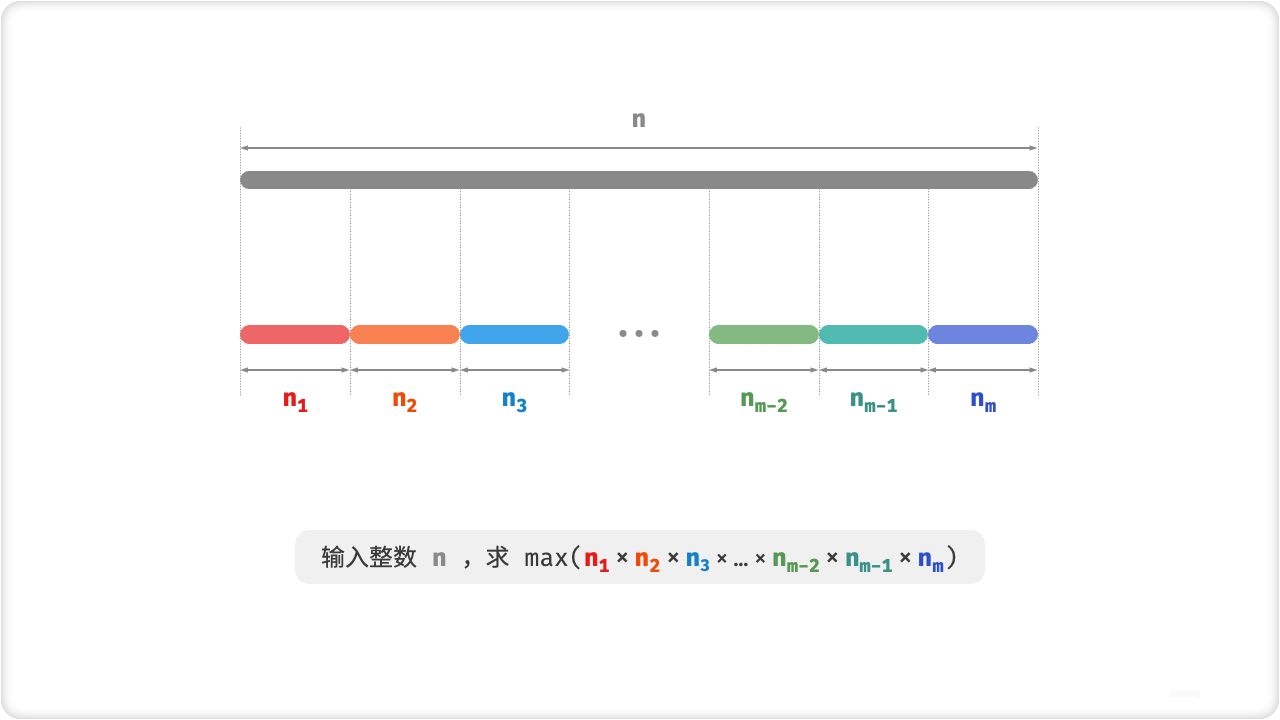
最大切分乘积问题是指将一个长度为n的绳子剪成m段,使得各段长度的乘积最大。贪心算法可以用来解决这个问题。
具体地,将绳子按照长度均分成m段,每段的长度为n/m。如果n/m的值为整数,则每段长度相等;否则,将前面的m - n % m段的长度加1,即可使得各段长度尽量接近且不超过n/m。然后计算各段长度的乘积并返回最大值即可。
以下是最大切分乘积问题的贪心算法的实现代码:
public class max_product_cutting {
/* 最大切分乘积:贪心 */
public int maxProductCutting(int n) {
// 当 n <= 3 时,必须切分出一个 1
if (n <= 3) {
return 1 * (n - 1);
}
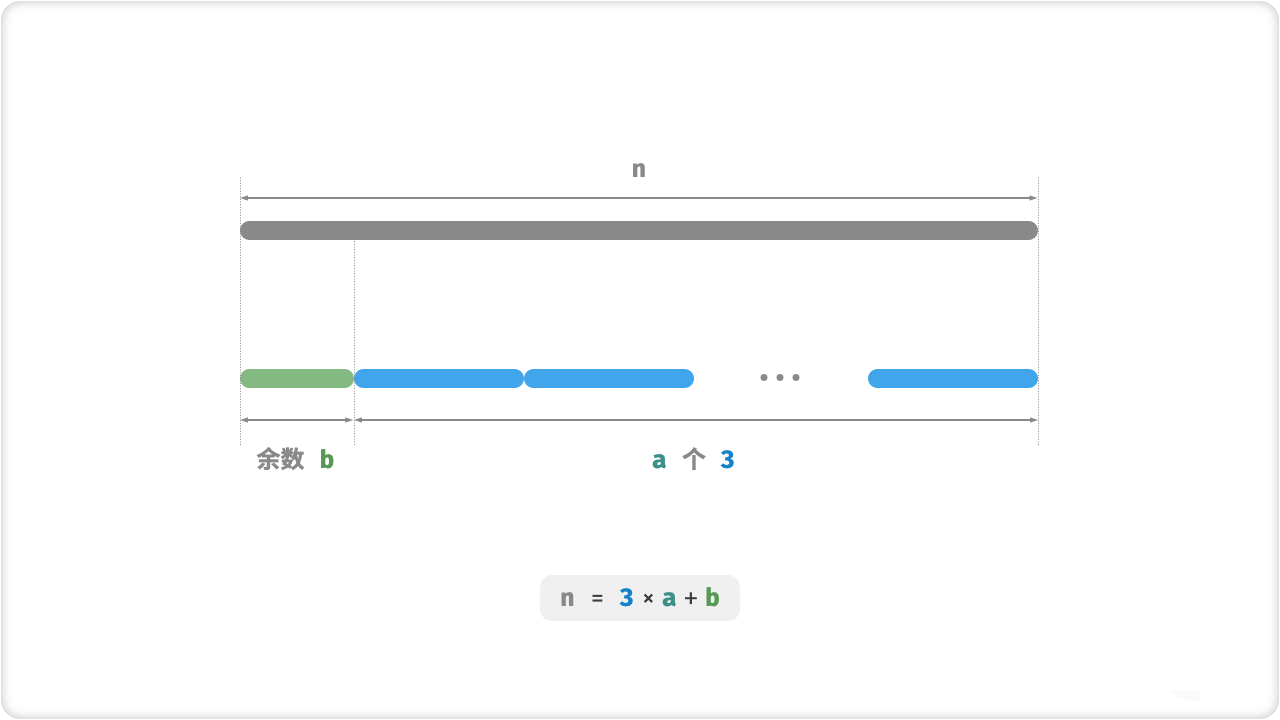
// 贪心地切分出 3 ,a 为 3 的个数,b 为余数
int a = n / 3;
int b = n % 3;
if (b == 1) {
// 当余数为 1 时,将一对 1 * 3 转化为 2 * 2
return (int)Math.Pow(3, a - 1) * 2 * 2;
}
if (b == 2) {
// 当余数为 2 时,不做处理
return (int)Math.Pow(3, a) * 2;
}
// 当余数为 0 时,不做处理
return (int)Math.Pow(3, a);
}
[Test]
public void Test() {
int n = 58;
// 贪心算法
int res = maxProductCutting(n);
Console.WriteLine("最大切分乘积为" + res);
}
}
🚀感谢:给读者的一封信
亲爱的读者,
我在这篇文章中投入了大量的心血和时间,希望为您提供有价值的内容。这篇文章包含了深入的研究和个人经验,我相信这些信息对您非常有帮助。
如果您觉得这篇文章对您有所帮助,我诚恳地请求您考虑赞赏1元钱的支持。这个金额不会对您的财务状况造成负担,但它会对我继续创作高质量的内容产生积极的影响。
我之所以写这篇文章,是因为我热爱分享有用的知识和见解。您的支持将帮助我继续这个使命,也鼓励我花更多的时间和精力创作更多有价值的内容。
如果您愿意支持我的创作,请扫描下面二维码,您的支持将不胜感激。同时,如果您有任何反馈或建议,也欢迎与我分享。

再次感谢您的阅读和支持!
最诚挚的问候, “愚公搬代码”
- 点赞
- 收藏
- 关注作者


评论(0)