🏆 作者简介，愚公搬代码
🏆《头衔》：华为云特约编辑，华为云云享专家，华为开发者专家，华为产品云测专家，CSDN博客专家，阿里云专家博主，腾讯云优秀博主，掘金优秀博主，51CTO博客专家等。
🏆《近期荣誉》：2022年CSDN博客之星TOP2，2022年华为云十佳博主等。
🏆《博客内容》：.NET、Java、Python、Go、Node、前端、IOS、Android、鸿蒙、Linux、物联网、网络安全、大数据、人工智能、U3D游戏、小程序等相关领域知识。
🏆🎉欢迎 👍点赞✍评论⭐收藏

🚀前言

五大常用算法的特点如下：

1. 分治：将一个大问题拆分成若干个小问题，分别解决，然后将解决结果合并起来得到整个问题的解。分治算法的特点是递归，效率高，但对数据的规律要求比较高，需要较高的算法设计技巧。常见应用领域为排序、查找和统计等。

2. 动态规划：将一个大问题分解成若干个小问题，通过寻找子问题之间的递推关系，求解小问题的最优解，然后将小问题的最优解组合起来解决整个大问题。动态规划的特点是可以解决具有重叠子问题的问题，但需要较高的时间和空间复杂度。常见应用领域为求解最大子序列、背包问题等。

3. 贪心：在处理问题的过程中，每次做出局部最优的选择，希望通过局部最优的选择达到全局最优。贪心算法的特点是快速、简单，但是无法保证每个局部最优解会导致全局最优解。常见应用领域为最小生成树、活动安排等。

4. 回溯：通过不断尝试局部的解，如果不满足要求就回溯返回，直到找到解为止。回溯算法的特点是可以解决多种类型的问题，但需要搜索所有可能的解，时间复杂度较高。常见应用领域为八皇后问题、排列组合问题等。

5. 分支限界：与回溯算法相似，但是在搜索的过程中，通过剪枝操作来减少搜索的空间，提高算法效率。常见应用领域为旅行商问题、图着色问题等。

🚀一、动态规划算法

🔎1.基本思想

动态规划算法的基本思想是将原问题分解为若干个子问题，并先求解子问题，再根据子问题的解得到原问题的解。这种方法的优点在于避免了重复计算，从而提高了算法的效率。

具体来说，动态规划算法的主要步骤包括：

1. 确定状态：将原问题化为子问题，并将子问题的解定义为状态。

2. 确定转移方程：根据子问题之间的关系，确定由一个状态转移到另一个状态的转移方程。

3. 确定边界条件：确定最小子问题的解，即边界条件。

4. 使用递推或记忆化搜索求解：利用转移方程和边界条件，从最小子问题开始逐步求解。

在实际应用中，动态规划算法通常需要用到一个数组或矩阵来存储子问题的解，以便在求解大问题时能够重复使用。此外，由于动态规划算法基于子问题求解，因此通常需要分析问题的子结构，以确定状态和转移方程。

public class climbing_stairs_backtrack {
    /* 回溯 */
    public void backtrack(List<int> choices, int state, int n, List<int> res) {
        // 当爬到第 n 阶时，方案数量加 1
        if (state == n)
            res[0]++;
        // 遍历所有选择
        foreach (int choice in choices) {
            // 剪枝：不允许越过第 n 阶
            if (state + choice > n)
                break;
            // 尝试：做出选择，更新状态
            backtrack(choices, state + choice, n, res);
            // 回退
        }
    }

    /* 爬楼梯：回溯 */
    public int climbingStairsBacktrack(int n) {
        List<int> choices = new List<int> { 1, 2 }; // 可选择向上爬 1 或 2 阶
        int state = 0; // 从第 0 阶开始爬
        List<int> res = new List<int> { 0 }; // 使用 res[0] 记录方案数量
        backtrack(choices, state, n, res);
        return res[0];
    }

    [Test]
    public void Test() {
        int n = 9;
        int res = climbingStairsBacktrack(n);
        Console.WriteLine($"爬 {n} 阶楼梯共有 {res} 种方案");
    }
}

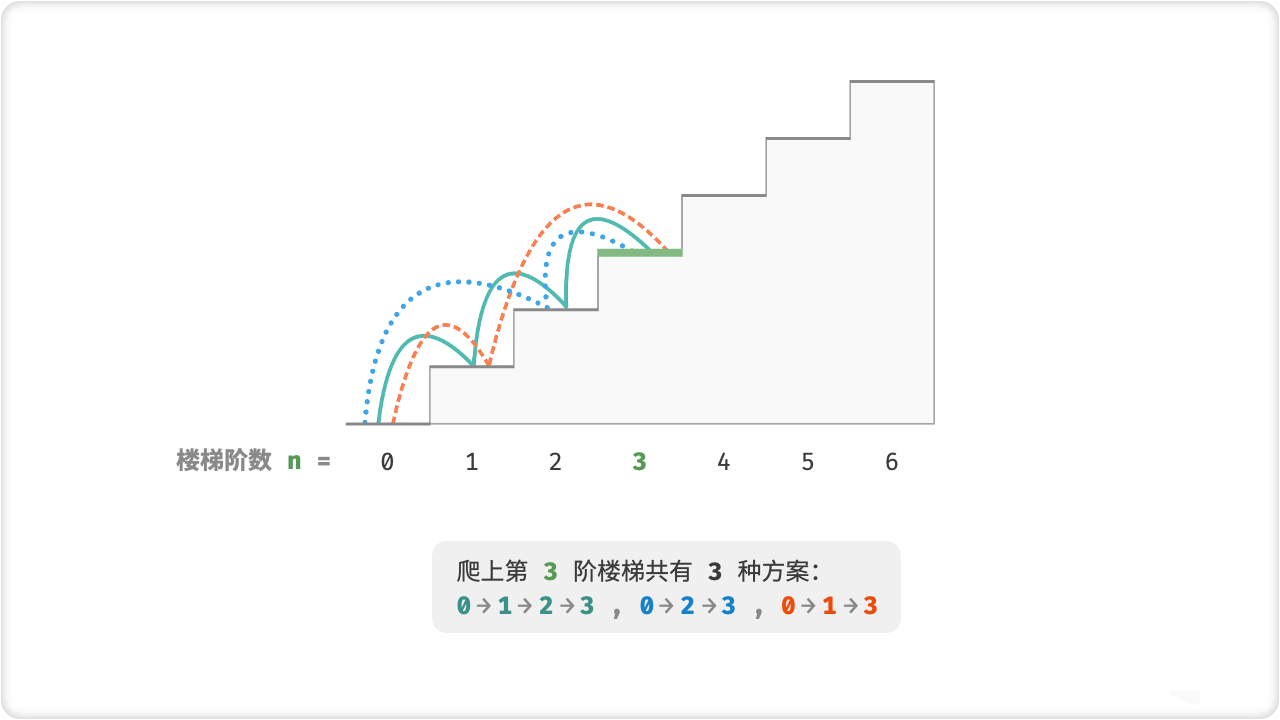
🦋1.1 暴力搜索

动态规划的本质是对问题进行状态转移，使得问题的规模减小，但是状态转移有时候需要涉及到不同的分支，这时候暴力搜索是一种常见的解决方法。

具体来说，暴力搜索就是对所有可能的状态进行遍历，找到最优的状态。适用于问题规模较小，但是状态数较多的问题。

举个例子，假如有一个背包问题，要求在一定的背包容量下，选取一些物品使得价值最大。这时候可以使用暴力搜索，对于每个物品，可以选择将其放入背包或者不放入背包，依次遍历所有可能的状态，选取最大价值。

但是，暴力搜索的时间复杂度很高，当问题规模较大时，无法高效求解。因此，在动态规划中，通常会结合其他优化方法，如记忆化搜索、剪枝等，使得算法能够高效求解。

public class climbing_stairs_dfs {
    /* 搜索 */
    public int dfs(int i) {
        // 已知 dp[1] 和 dp[2] ，返回之
        if (i == 1 || i == 2)
            return i;
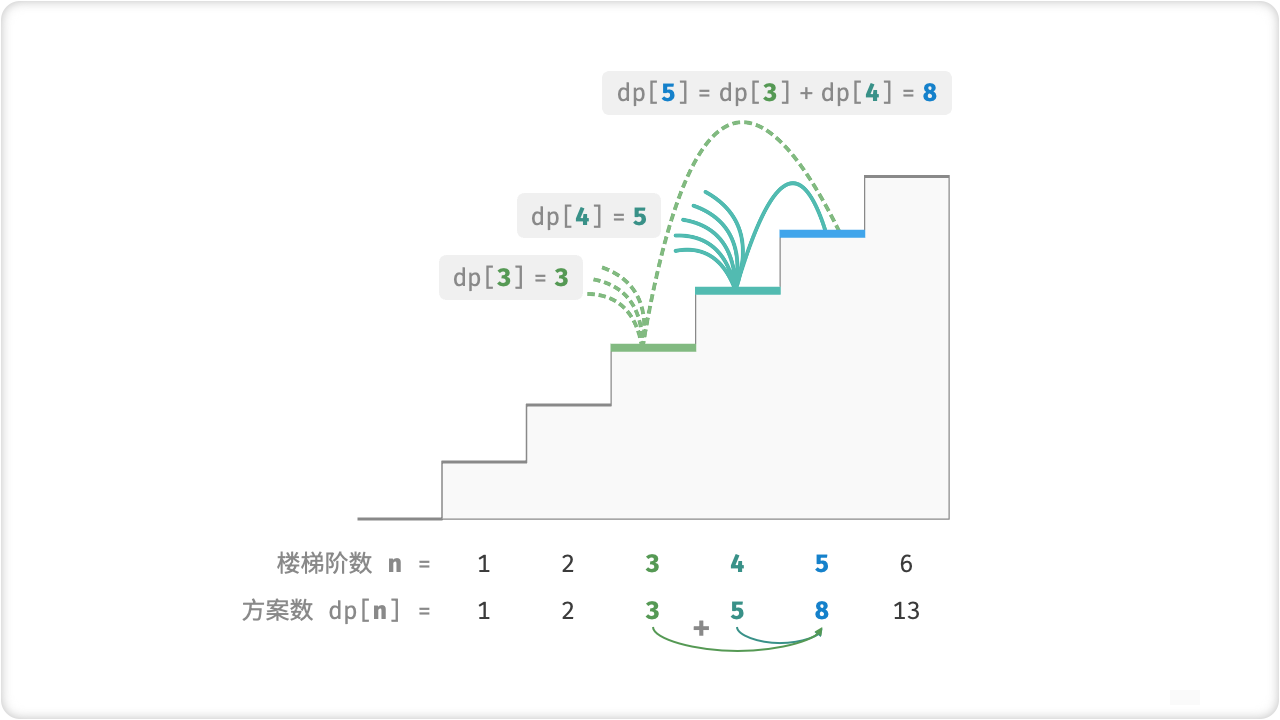
        // dp[i] = dp[i-1] + dp[i-2]
        int count = dfs(i - 1) + dfs(i - 2);
        return count;
    }

    /* 爬楼梯：搜索 */
    public int climbingStairsDFS(int n) {
        return dfs(n);
    }

    [Test]
    public void Test() {
        int n = 9;
        int res = climbingStairsDFS(n);
        Console.WriteLine($"爬 {n} 阶楼梯共有 {res} 种方案");
    }
}

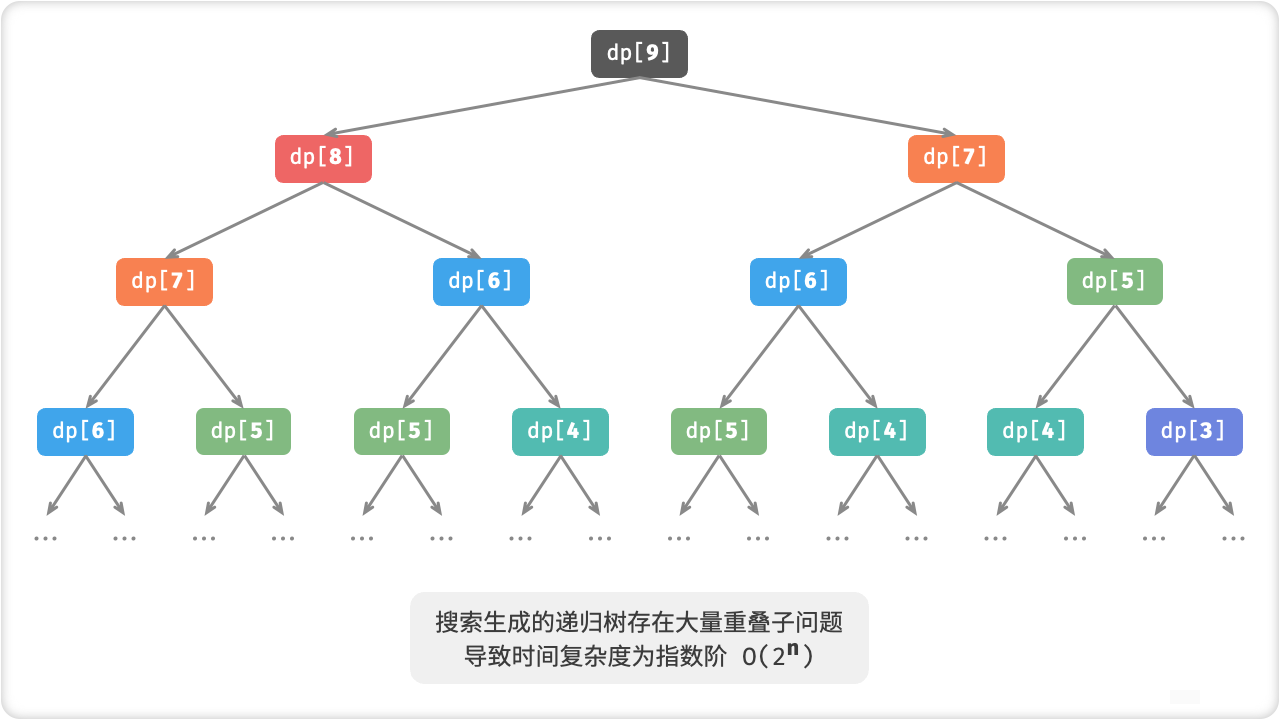
🦋1.2 记忆化搜索

记忆化搜索（Memoization）是动态规划的一种优化方法，也叫做“记忆化递归”。记忆化搜索通过将子问题的结果保存下来，避免重复计算，以减少计算时间。

常见的动态规划问题通常满足“最优子结构”和“重叠子问题”的性质，即子问题的解可以被复用，而且每个子问题可能会被计算多次。将已解决的子问题的结果保存在一个数组或者哈希表中，当需要计算相同的子问题时，就可以直接返回之前计算的结果，而不必再次递归计算。

public class climbing_stairs_dfs_mem {
    /* 记忆化搜索 */
    public int dfs(int i, int[] mem) {
        // 已知 dp[1] 和 dp[2] ，返回之
        if (i == 1 || i == 2)
            return i;
        // 若存在记录 dp[i] ，则直接返回之
        if (mem[i] != -1)
            return mem[i];
        // dp[i] = dp[i-1] + dp[i-2]
        int count = dfs(i - 1, mem) + dfs(i - 2, mem);
        // 记录 dp[i]
        mem[i] = count;
        return count;
    }

    /* 爬楼梯：记忆化搜索 */
    public int climbingStairsDFSMem(int n) {
        // mem[i] 记录爬到第 i 阶的方案总数，-1 代表无记录
        int[] mem = new int[n + 1];
        Array.Fill(mem, -1);
        return dfs(n, mem);
    }

    [Test]
    public void Test() {
        int n = 9;
        int res = climbingStairsDFSMem(n);
        Console.WriteLine($"爬 {n} 阶楼梯共有 {res} 种方案");
    }
}

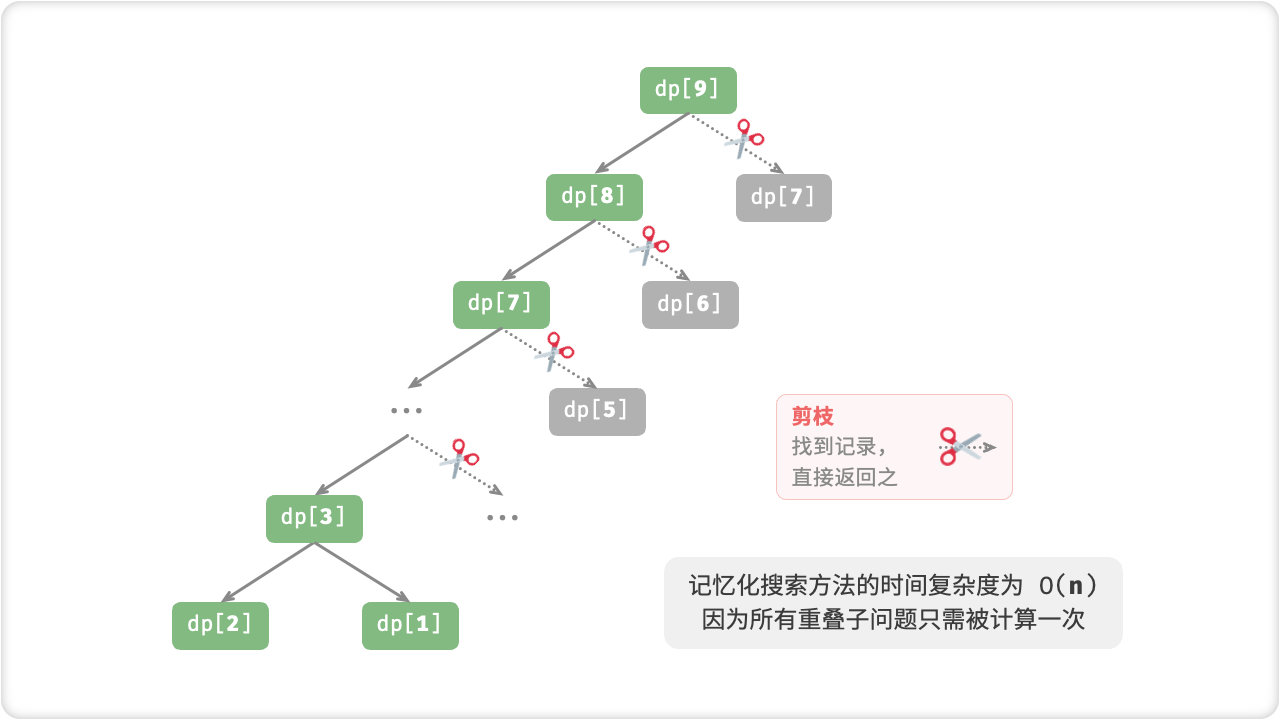
🦋1.3 动态规划

记忆化搜索是一种“从顶至底”的方法：我们从原问题（根节点）开始，递归地将较大子问题分解为较小子问题，直至解已知的最小子问题（叶节点）。之后，通过回溯将子问题的解逐层收集，构建出原问题的解。

与之相反，动态规划是一种“从底至顶”的方法：从最小子问题的解开始，迭代地构建更大子问题的解，直至得到原问题的解。

由于动态规划不包含回溯过程，因此只需使用循环迭代实现，无须使用递归。在以下代码中，我们初始化一个数组 dp 来存储子问题的解，它起到了记忆化搜索中数组 mem 相同的记录作用。

public class climbing_stairs_dp {
    /* 爬楼梯：动态规划 */
    public int climbingStairsDP(int n) {
        if (n == 1 || n == 2)
            return n;
        // 初始化 dp 表，用于存储子问题的解
        int[] dp = new int[n + 1];
        // 初始状态：预设最小子问题的解
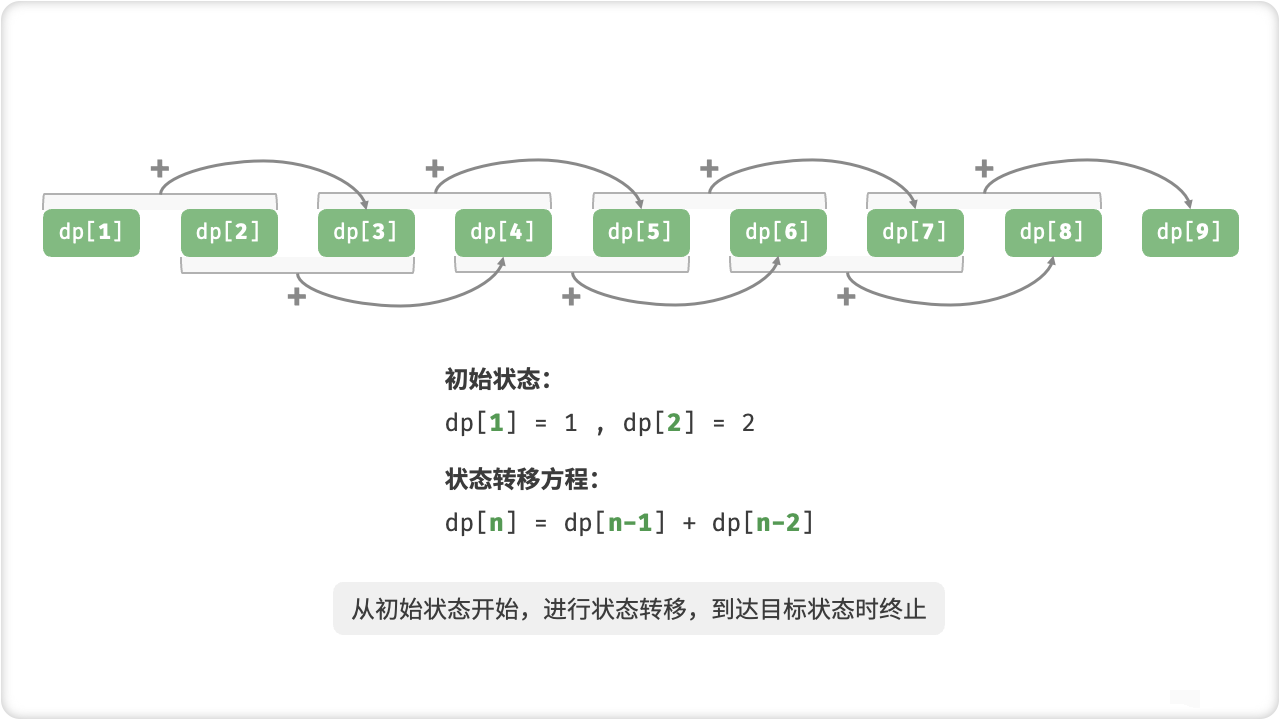
        dp[1] = 1;
        dp[2] = 2;
        // 状态转移：从较小子问题逐步求解较大子问题
        for (int i = 3; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }

    /* 爬楼梯：空间优化后的动态规划 */
    public int climbingStairsDPComp(int n) {
        if (n == 1 || n == 2)
            return n;
        int a = 1, b = 2;
        for (int i = 3; i <= n; i++) {
            int tmp = b;
            b = a + b;
            a = tmp;
        }
        return b;
    }

    [Test]
    public void Test() {
        int n = 9;

        int res = climbingStairsDP(n);
        Console.WriteLine($"爬 {n} 阶楼梯共有 {res} 种方案");

        res = climbingStairsDPComp(n);
        Console.WriteLine($"爬 {n} 阶楼梯共有 {res} 种方案");
    }
}

🔎2.动态规划问题特性

在分治、动态规划、回溯中的侧重点不同。

• 分治算法递归地将原问题划分为多个相互独立的子问题，直至最小子问题，并在回溯中合并子问题的解，最终得到原问题的解。

• 动态规划也对问题进行递归分解，但与分治算法的主要区别是，动态规划中的子问题是相互依赖的，在分解过程中会出现许多重叠子问题。

• 回溯算法在尝试和回退中穷举所有可能的解，并通过剪枝避免不必要的搜索分支。原问题的解由一系列决策步骤构成，我们可以将每个决策步骤之前的子序列看作为一个子问题。

实际上，动态规划常用来求解最优化问题，它们不仅包含重叠子问题，还具有另外两大特性：最优子结构、无后效性。

🦋2.1 最优子结构

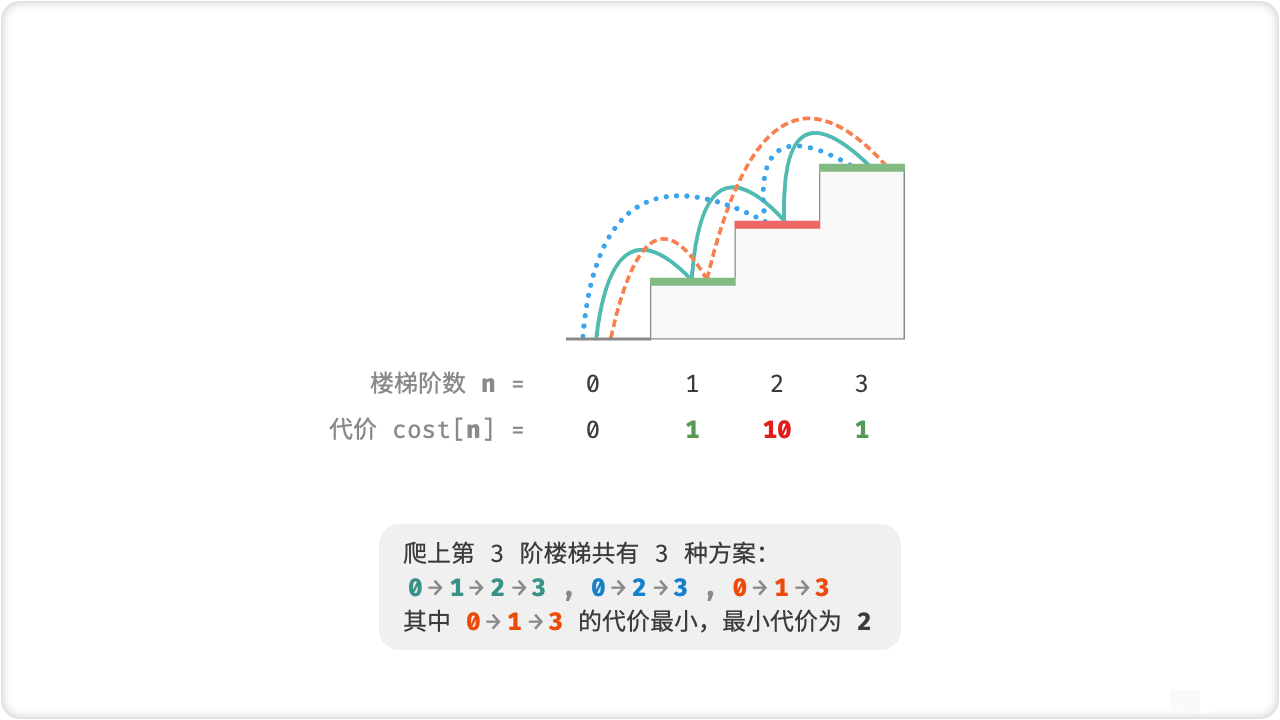
给定一个楼梯，你每步可以上 (1) 阶或者 (2) 阶，每一阶楼梯上都贴有一个非负整数，表示你在该台阶所需要付出的代价。给定一个非负整数数组 (cost) ，其中 (cost[i]) 表示在第 (i) 个台阶需要付出的代价，(cost[0]) 为地面起始点。

public class min_cost_climbing_stairs_dp {
    /* 爬楼梯最小代价：动态规划 */
    public int minCostClimbingStairsDP(int[] cost) {
        int n = cost.Length - 1;
        if (n == 1 || n == 2)
            return cost[n];
        // 初始化 dp 表，用于存储子问题的解
        int[] dp = new int[n + 1];
        // 初始状态：预设最小子问题的解
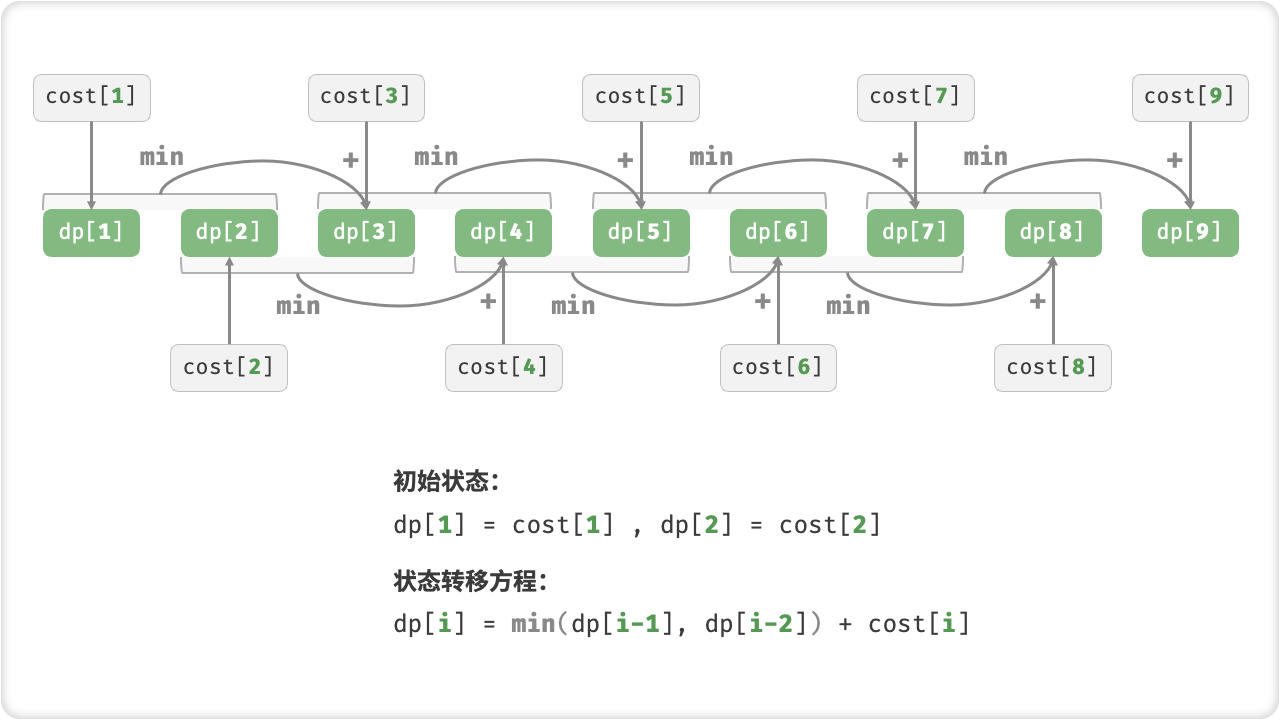
        dp[1] = cost[1];
        dp[2] = cost[2];
        // 状态转移：从较小子问题逐步求解较大子问题
        for (int i = 3; i <= n; i++) {
            dp[i] = Math.Min(dp[i - 1], dp[i - 2]) + cost[i];
        }
        return dp[n];
    }

    /* 爬楼梯最小代价：空间优化后的动态规划 */
    public int minCostClimbingStairsDPComp(int[] cost) {
        int n = cost.Length - 1;
        if (n == 1 || n == 2)
            return cost[n];
        int a = cost[1], b = cost[2];
        for (int i = 3; i <= n; i++) {
            int tmp = b;
            b = Math.Min(a, tmp) + cost[i];
            a = tmp;
        }
        return b;
    }

    [Test]
    public void Test() {
        int[] cost = { 0, 1, 10, 1, 1, 1, 10, 1, 1, 10, 1 };
        Console.WriteLine("输入楼梯的代价列表为");
        PrintUtil.PrintList(cost);

        int res = minCostClimbingStairsDP(cost);
        Console.WriteLine($"爬完楼梯的最低代价为 {res}");

        res = minCostClimbingStairsDPComp(cost);
        Console.WriteLine($"爬完楼梯的最低代价为 {res}");
    }
}

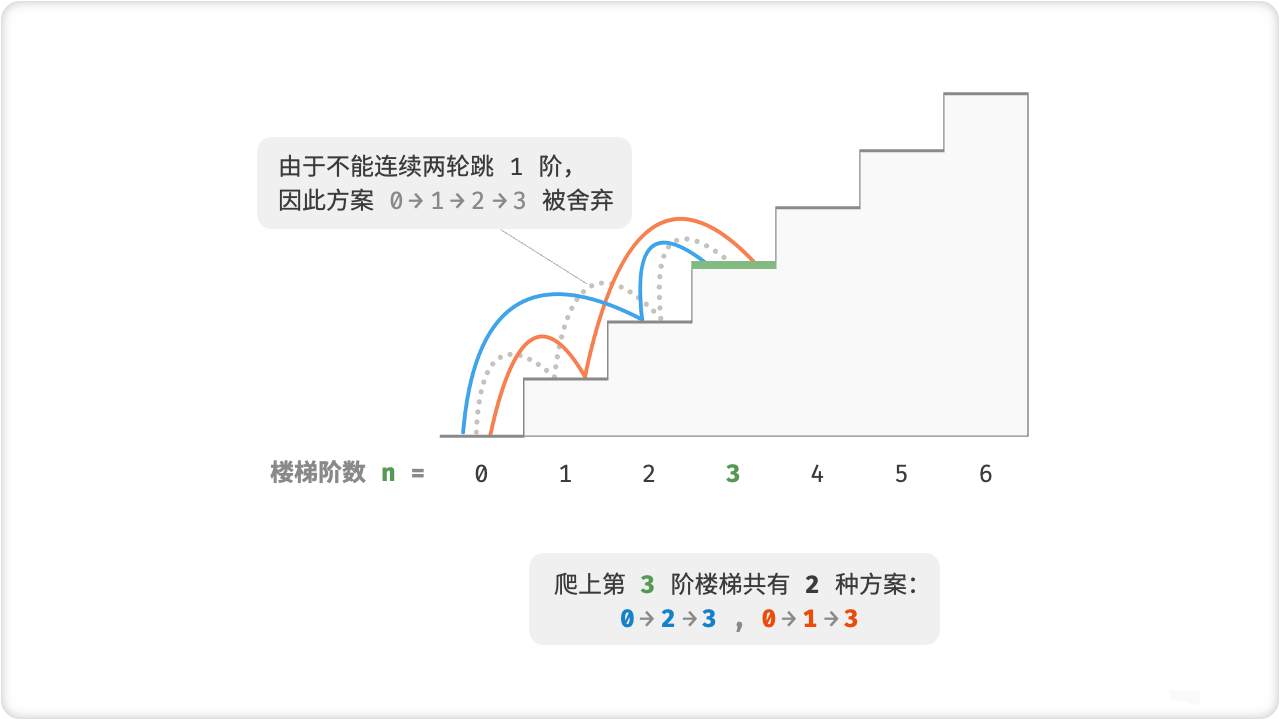
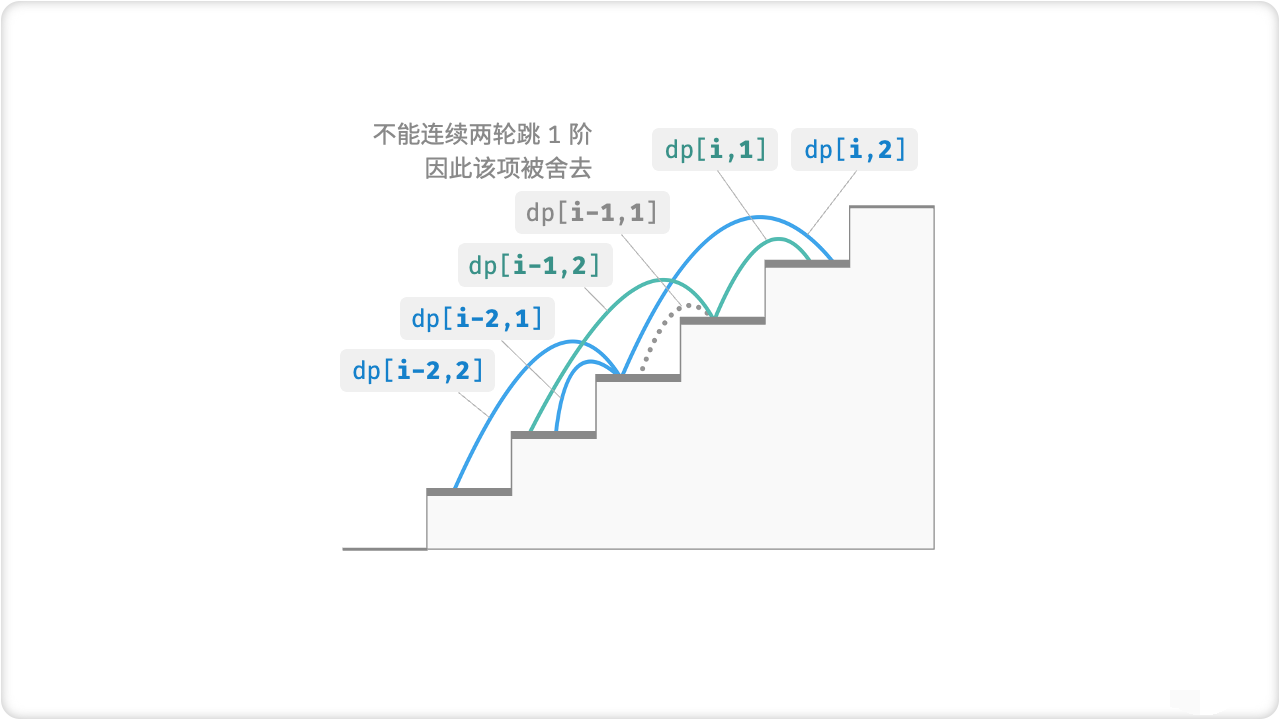
🦋2.2 无后效性

无后效性是动态规划能够有效解决问题的重要特性之一，定义为：给定一个确定的状态，它的未来发展只与当前状态有关，而与当前状态过去所经历过的所有状态无关。

namespace hello_algo.chapter_dynamic_programming;

public class climbing_stairs_constraint_dp {
    /* 带约束爬楼梯：动态规划 */
    public int climbingStairsConstraintDP(int n) {
        if (n == 1 || n == 2) {
            return 1;
        }
        // 初始化 dp 表，用于存储子问题的解
        int[,] dp = new int[n + 1, 3];
        // 初始状态：预设最小子问题的解
        dp[1, 1] = 1;
        dp[1, 2] = 0;
        dp[2, 1] = 0;
        dp[2, 2] = 1;
        // 状态转移：从较小子问题逐步求解较大子问题
        for (int i = 3; i <= n; i++) {
            dp[i, 1] = dp[i - 1, 2];
            dp[i, 2] = dp[i - 2, 1] + dp[i - 2, 2];
        }
        return dp[n, 1] + dp[n, 2];
    }

    [Test]
    public void Test() {
        int n = 9;
        int res = climbingStairsConstraintDP(n);
        Console.WriteLine($"爬 {n} 阶楼梯共有 {res} 种方案");
    }
}

🔎3.动态规划问题解题思路

动态规划算法通常适用于具有一定规律性、能够被划分成若干个相同或相似的子问题的问题。一般来说，一个问题能够用动态规划求解，需要满足以下两个条件：

1. 该问题具有最优子结构：即原问题的最优解可以通过其子问题的最优解来构建。这意味着，我们可以通过分解问题为若干个相似的子问题来求解整个问题，从而得到问题的最优解。

2. 该问题的子问题重叠：即不同的子问题会涉及到相同的子问题。这意味着，我们可以利用子问题的最优解来避免重复计算，提高计算效率。

一些常见的适合用动态规划求解的问题包括：

1. 背包问题（0/1背包、完全背包、多重背包等）

2. 最长公共子序列问题

3. 最短路径问题

4. 最大独立集问题

5. 最优二叉搜索树问题

6. 最长上升子序列问题

7. 最大子矩阵问题

8. 斐波那契数列等数学问题

动态规划算法适用于那些能够被分解成若干个相似的子问题，并且这些子问题具有最优子结构和重叠子问题的问题。

🦋3.1 问题判断

动态规划的解题流程会因问题的性质和难度而有所不同，但通常遵循以下步骤：描述决策，定义状态，建立 (dp) 表，推导状态转移方程，确定边界条件等。

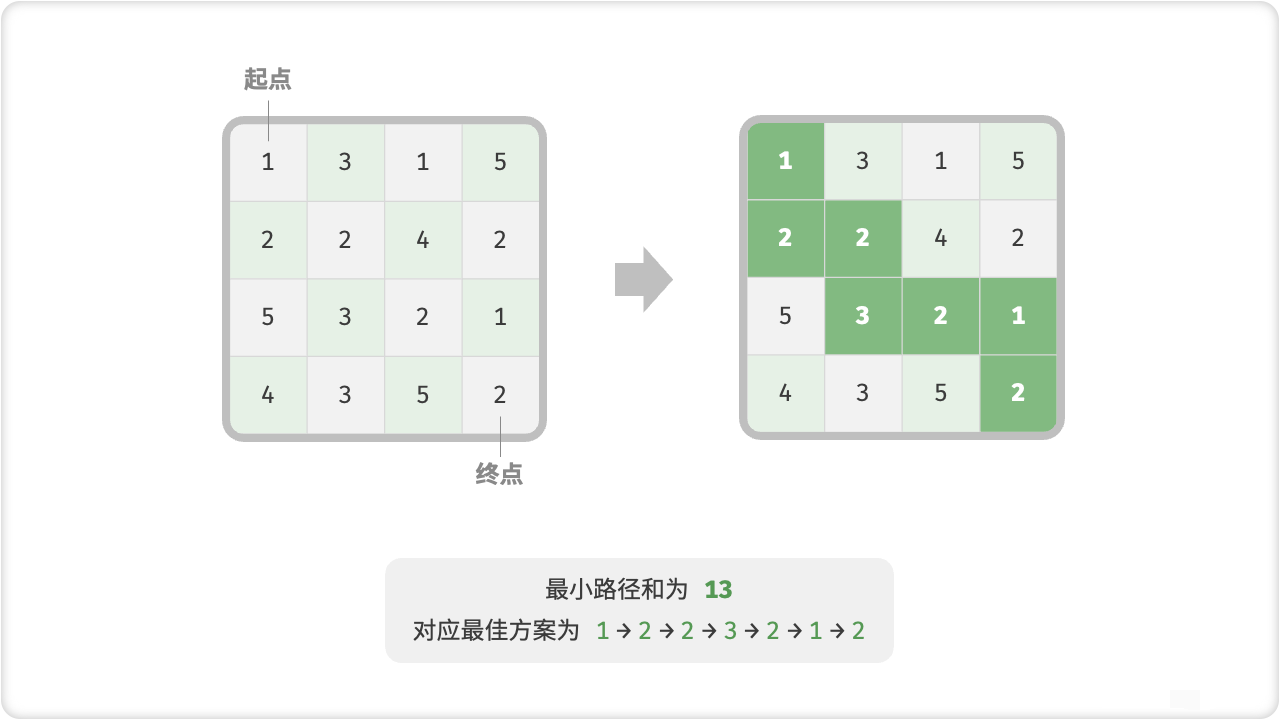
第一步：思考每轮的决策，定义状态，从而得到 (dp) 表

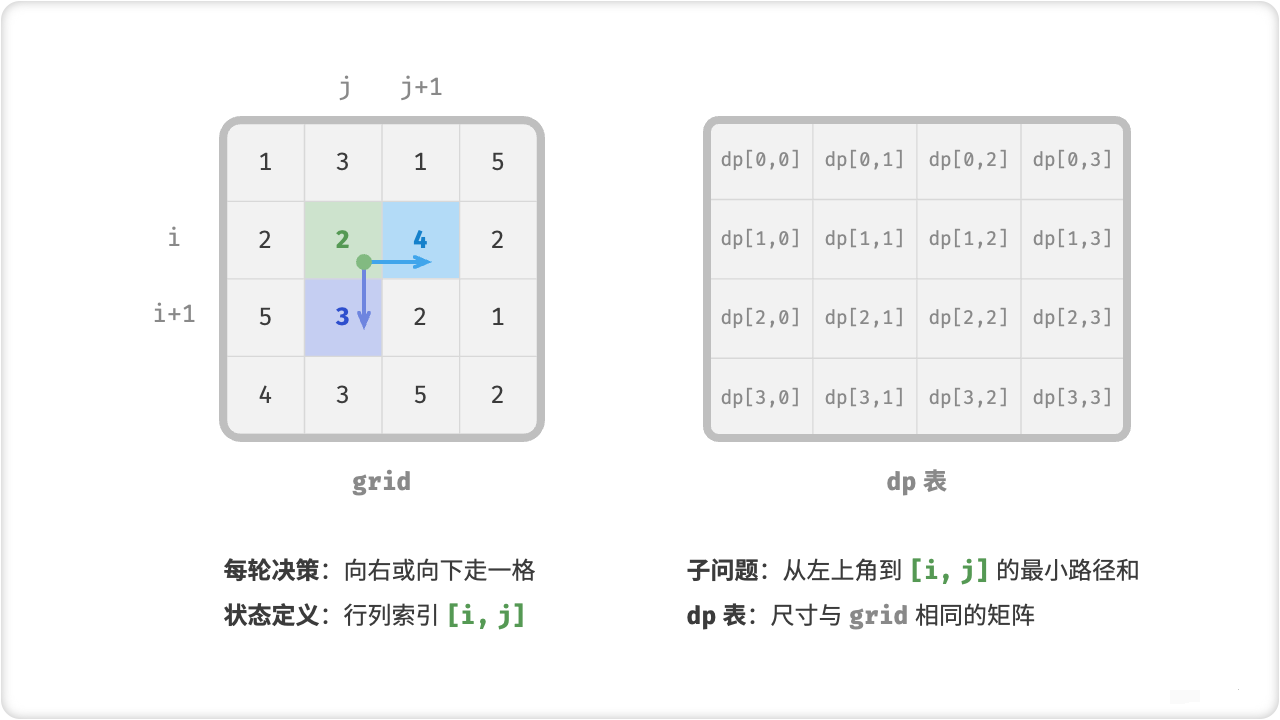
第二步：找出最优子结构，进而推导出状态转移方程

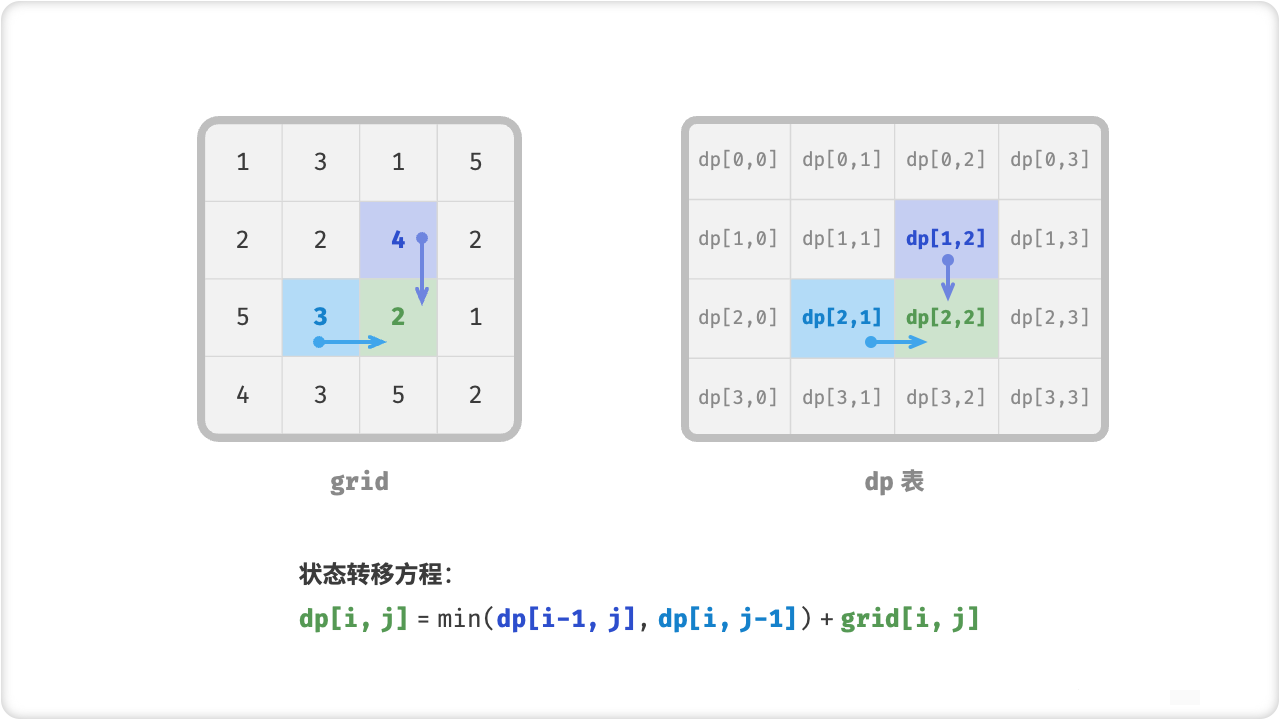
第三步：确定边界条件和状态转移顺序

🦋3.2 问题求解步骤

子问题分解是一种从顶至底的思想，因此按照“暴力搜索 (\rightarrow) 记忆化搜索 (\rightarrow) 动态规划”的顺序实现更加符合思维习惯。

/**
* File: min_path_sum.cs
* Created Time: 2023-07-10
* Author: hpstory (hpstory1024@163.com)
*/

namespace hello_algo.chapter_dynamic_programming;

public class min_path_sum {
    /* 最小路径和：暴力搜索 */
    public int minPathSumDFS(int[][] grid, int i, int j) {
        // 若为左上角单元格，则终止搜索
        if (i == 0 && j == 0) {
            return grid[0][0];
        }
        // 若行列索引越界，则返回 +∞ 代价
        if (i < 0 || j < 0) {
            return int.MaxValue;
        }
        // 计算从左上角到 (i-1, j) 和 (i, j-1) 的最小路径代价
        int left = minPathSumDFS(grid, i - 1, j);
        int up = minPathSumDFS(grid, i, j - 1);
        // 返回从左上角到 (i, j) 的最小路径代价
        return Math.Min(left, up) + grid[i][j];
    }

    /* 最小路径和：记忆化搜索 */
    public int minPathSumDFSMem(int[][] grid, int[][] mem, int i, int j) {
        // 若为左上角单元格，则终止搜索
        if (i == 0 && j == 0) {
            return grid[0][0];
        }
        // 若行列索引越界，则返回 +∞ 代价
        if (i < 0 || j < 0) {
            return int.MaxValue;
        }
        // 若已有记录，则直接返回
        if (mem[i][j] != -1) {
            return mem[i][j];
        }
        // 左边和上边单元格的最小路径代价
        int left = minPathSumDFSMem(grid, mem, i - 1, j);
        int up = minPathSumDFSMem(grid, mem, i, j - 1);
        // 记录并返回左上角到 (i, j) 的最小路径代价
        mem[i][j] = Math.Min(left, up) + grid[i][j];
        return mem[i][j];
    }

    /* 最小路径和：动态规划 */
    public int minPathSumDP(int[][] grid) {
        int n = grid.Length, m = grid[0].Length;
        // 初始化 dp 表
        int[,] dp = new int[n, m];
        dp[0, 0] = grid[0][0];
        // 状态转移：首行
        for (int j = 1; j < m; j++) {
            dp[0, j] = dp[0, j - 1] + grid[0][j];
        }
        // 状态转移：首列
        for (int i = 1; i < n; i++) {
            dp[i, 0] = dp[i - 1, 0] + grid[i][0];
        }
        // 状态转移：其余行列
        for (int i = 1; i < n; i++) {
            for (int j = 1; j < m; j++) {
                dp[i, j] = Math.Min(dp[i, j - 1], dp[i - 1, j]) + grid[i][j];
            }
        }
        return dp[n - 1, m - 1];
    }

    /* 最小路径和：空间优化后的动态规划 */
    public int minPathSumDPComp(int[][] grid) {
        int n = grid.Length, m = grid[0].Length;
        // 初始化 dp 表
        int[] dp = new int[m];
        dp[0] = grid[0][0];
        // 状态转移：首行
        for (int j = 1; j < m; j++) {
            dp[j] = dp[j - 1] + grid[0][j];
        }
        // 状态转移：其余行
        for (int i = 1; i < n; i++) {
            // 状态转移：首列
            dp[0] = dp[0] + grid[i][0];
            // 状态转移：其余列
            for (int j = 1; j < m; j++) {
                dp[j] = Math.Min(dp[j - 1], dp[j]) + grid[i][j];
            }
        }
        return dp[m - 1];
    }

    [Test]
    public void Test() {
        int[][] grid =
        {
            new int[4] { 1, 3, 1, 5 },
            new int[4] { 2, 2, 4, 2 },
            new int[4] { 5, 3, 2, 1 },
            new int[4] { 4, 3, 5, 2 }
        };

        int n = grid.Length, m = grid[0].Length;

        // 暴力搜索
        int res = minPathSumDFS(grid, n - 1, m - 1);
        Console.WriteLine("从左上角到右下角的做小路径和为 " + res);

        // 记忆化搜索
        int[][] mem = new int[n][];
        for (int i = 0; i < n; i++) {
            mem[i] = new int[m];
            Array.Fill(mem[i], -1);
        }
        res = minPathSumDFSMem(grid, mem, n - 1, m - 1);
        Console.WriteLine("从左上角到右下角的做小路径和为 " + res);

        // 动态规划
        res = minPathSumDP(grid);
        Console.WriteLine("从左上角到右下角的做小路径和为 " + res);

        // 空间优化后的动态规划
        res = minPathSumDPComp(grid);
        Console.WriteLine("从左上角到右下角的做小路径和为 " + res);
    }
}

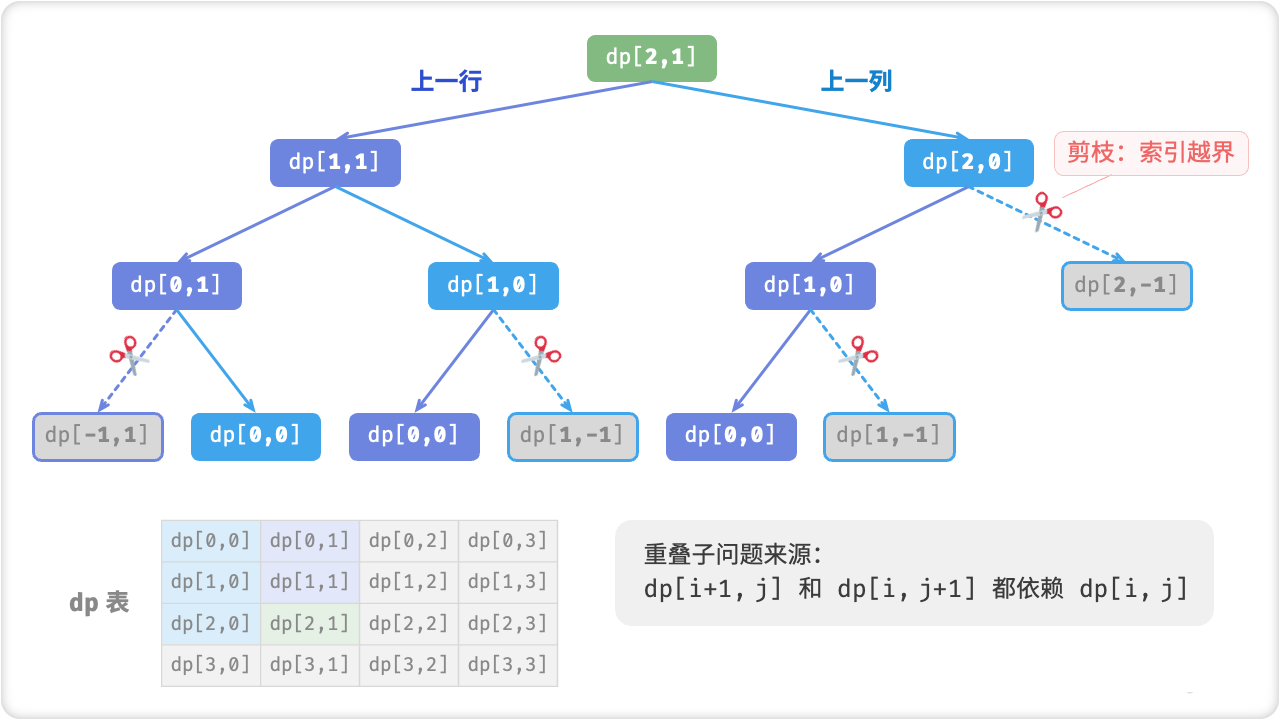
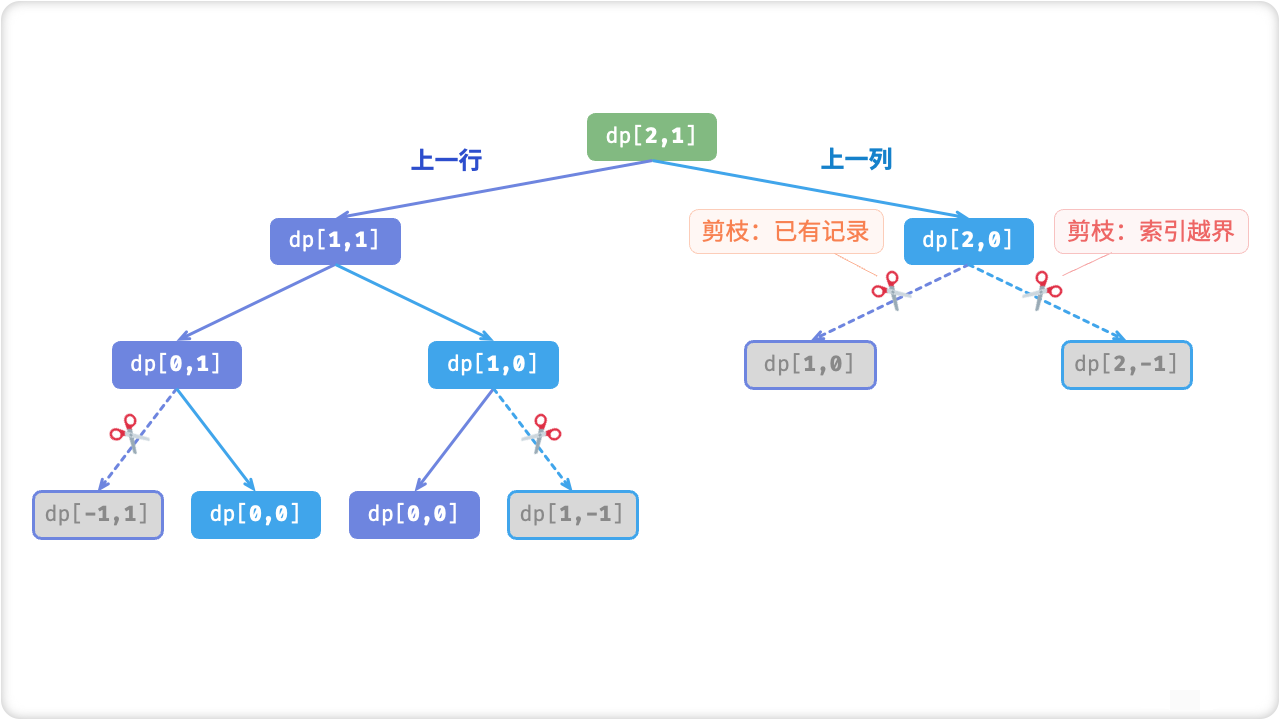
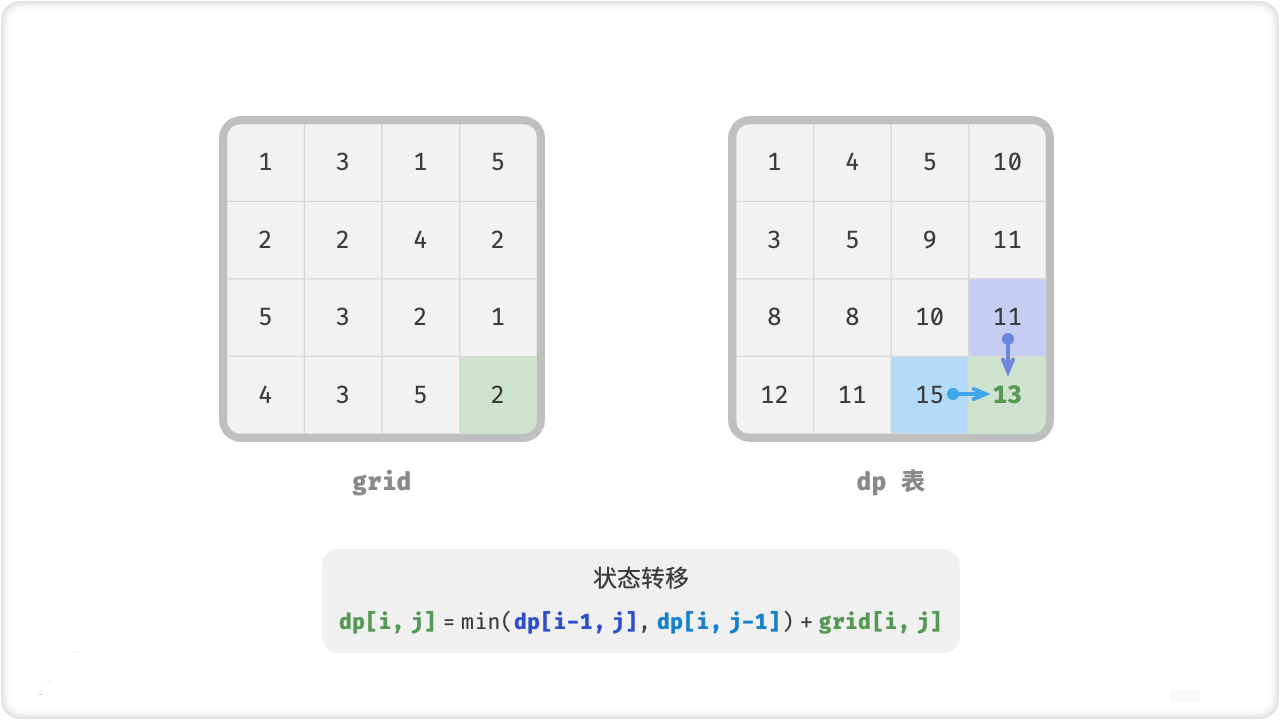
🔎4.0-1 背包问题

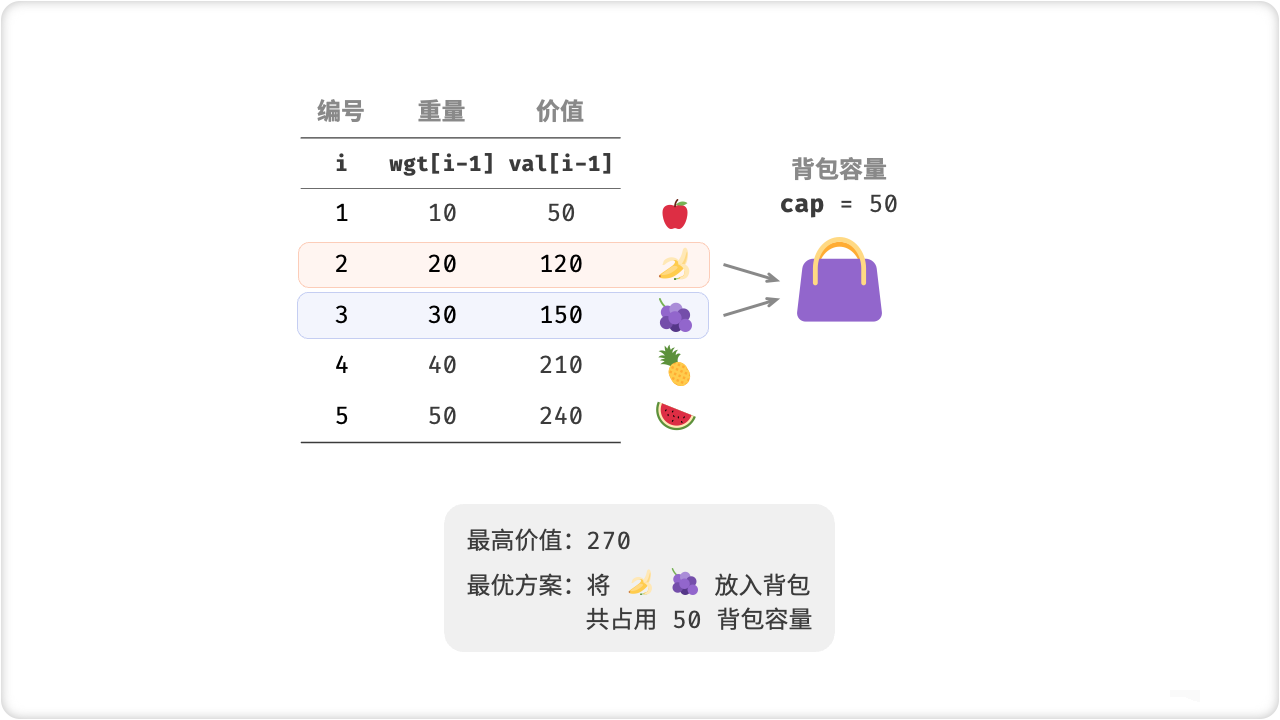
0-1背包问题是动态规划算法中的一种典型问题，指在限定总重量的情况下，选择若干个物品，使得这些物品的总体积不超过总重量，且价值最大。具体来说，给定n个物品，每个物品有一个重量wi和一个价值vi，以及一个总容量W，求从这些物品中选取若干物品，使得它们的总重量不超过W，且它们的总价值最大。

解决该问题的动态规划算法是：

1. 定义状态：设f(i,j)表示前i个物品中选择若干个，总重量不超过j的情况下可以获得的最大价值。

2. 定义状态转移方程：对于每个物品i，可以选择放入或不放入背包中，如果不放入，则f(i,j)=f(i-1,j)；如果选择放入，则f(i,j)=f(i-1,j-wi)+vi；因此：f(i,j)=max{f(i-1,j), f(i-1,j-wi)+vi}。

3. 初始化：f(0,j)=0，f(i,0)=0。

4. 根据状态转移方程进行状态转移，计算f(i,j)的值。

5. 最终结果：f(n,W)即为最优解。

该算法的时间复杂度为O(nW)，其中n为物品个数，W为总容量。由于每个物品最多只有两种状态（放入或不放入），因此该算法被称为“0-1背包问题”。

public class knapsack {
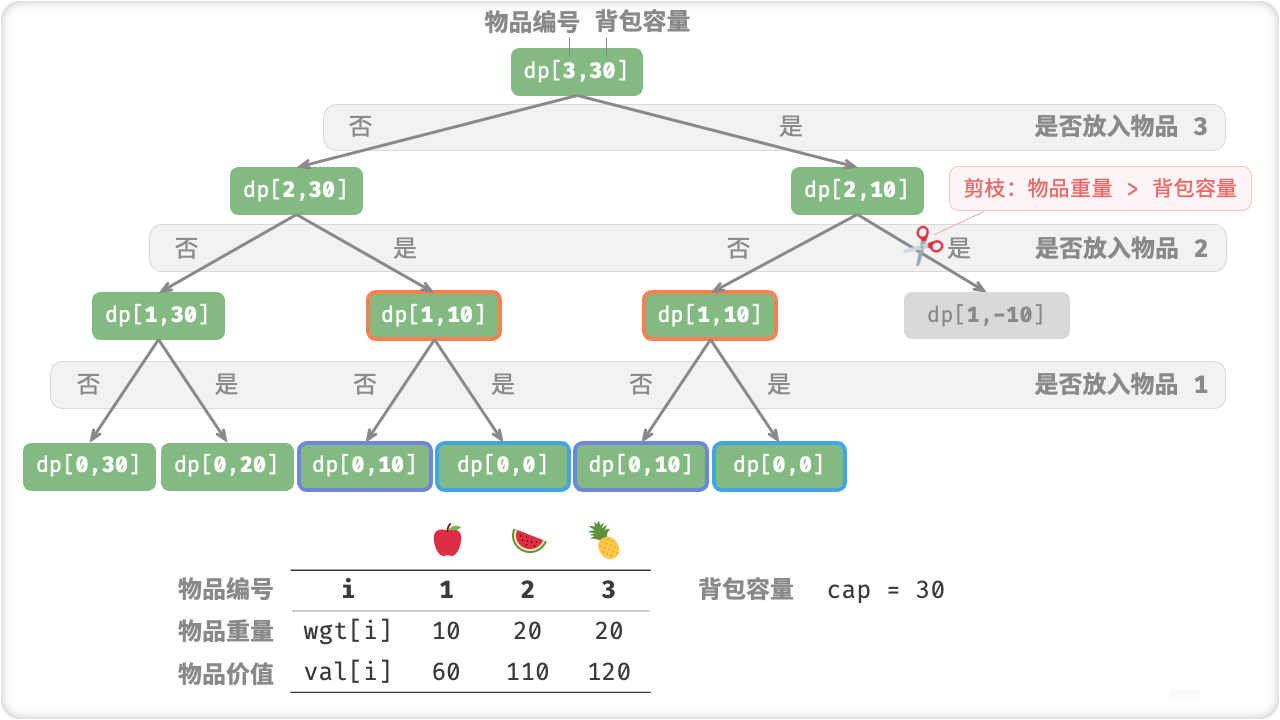
    /* 0-1 背包：暴力搜索 */
    public int knapsackDFS(int[] weight, int[] val, int i, int c) {
        // 若已选完所有物品或背包无容量，则返回价值 0
        if (i == 0 || c == 0) {
            return 0;
        }
        // 若超过背包容量，则只能不放入背包
        if (weight[i - 1] > c) {
            return knapsackDFS(weight, val, i - 1, c);
        }
        // 计算不放入和放入物品 i 的最大价值
        int no = knapsackDFS(weight, val, i - 1, c);
        int yes = knapsackDFS(weight, val, i - 1, c - weight[i - 1]) + val[i - 1];
        // 返回两种方案中价值更大的那一个
        return Math.Max(no, yes);
    }

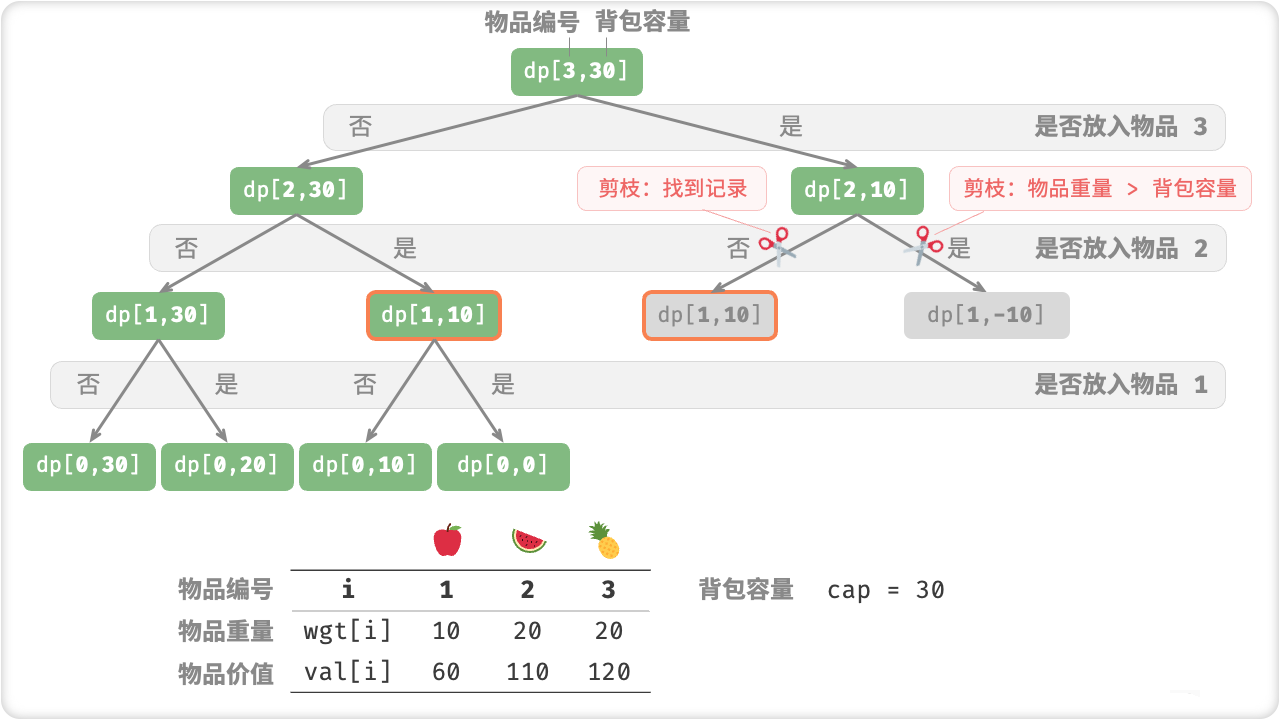
    /* 0-1 背包：记忆化搜索 */
    public int knapsackDFSMem(int[] weight, int[] val, int[][] mem, int i, int c) {
        // 若已选完所有物品或背包无容量，则返回价值 0
        if (i == 0 || c == 0) {
            return 0;
        }
        // 若已有记录，则直接返回
        if (mem[i][c] != -1) {
            return mem[i][c];
        }
        // 若超过背包容量，则只能不放入背包
        if (weight[i - 1] > c) {
            return knapsackDFSMem(weight, val, mem, i - 1, c);
        }
        // 计算不放入和放入物品 i 的最大价值
        int no = knapsackDFSMem(weight, val, mem, i - 1, c);
        int yes = knapsackDFSMem(weight, val, mem, i - 1, c - weight[i - 1]) + val[i - 1];
        // 记录并返回两种方案中价值更大的那一个
        mem[i][c] = Math.Max(no, yes);
        return mem[i][c];
    }

    /* 0-1 背包：动态规划 */
    public int knapsackDP(int[] weight, int[] val, int cap) {
        int n = weight.Length;
        // 初始化 dp 表
        int[,] dp = new int[n + 1, cap + 1];
        // 状态转移
        for (int i = 1; i <= n; i++) {
            for (int c = 1; c <= cap; c++) {
                if (weight[i - 1] > c) {
                    // 若超过背包容量，则不选物品 i
                    dp[i, c] = dp[i - 1, c];
                } else {
                    // 不选和选物品 i 这两种方案的较大值
                    dp[i, c] = Math.Max(dp[i - 1, c - weight[i - 1]] + val[i - 1], dp[i - 1, c]);
                }
            }
        }
        return dp[n, cap];
    }

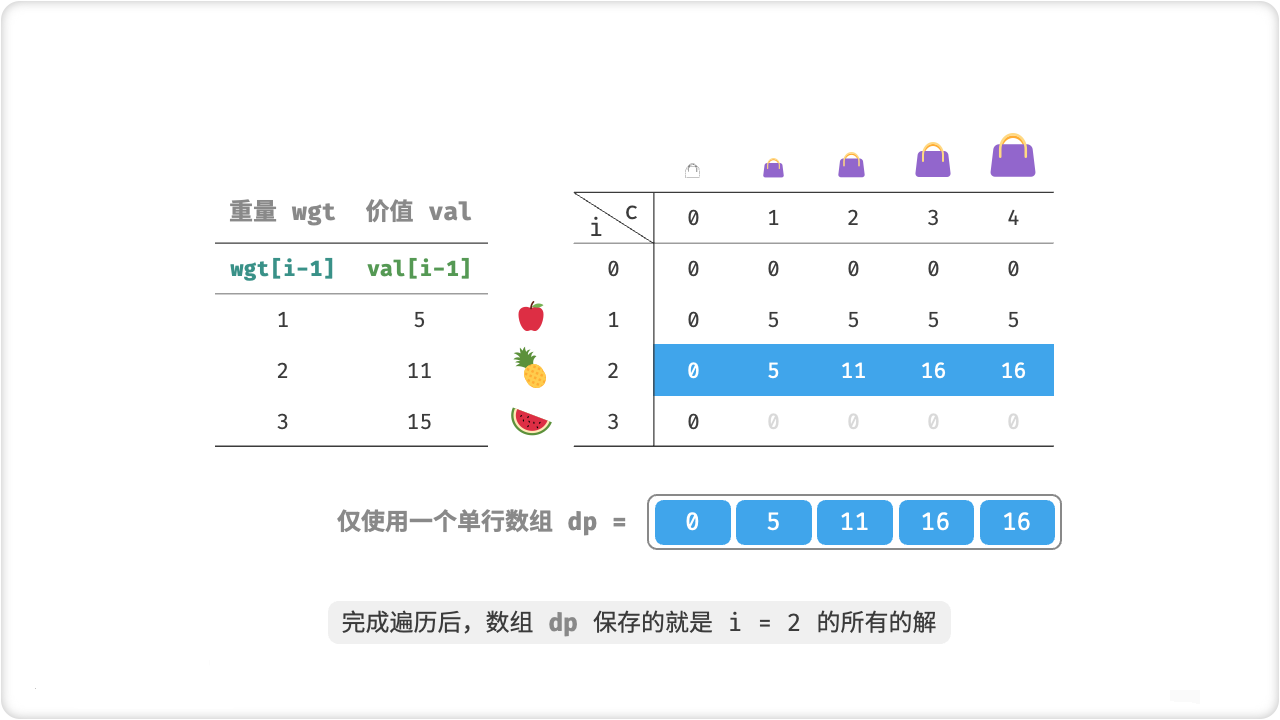
    /* 0-1 背包：空间优化后的动态规划 */
    public int knapsackDPComp(int[] weight, int[] val, int cap) {
        int n = weight.Length;
        // 初始化 dp 表
        int[] dp = new int[cap + 1];
        // 状态转移
        for (int i = 1; i <= n; i++) {
            // 倒序遍历
            for (int c = cap; c > 0; c--) {
                if (weight[i - 1] > c) {
                    // 若超过背包容量，则不选物品 i
                    dp[c] = dp[c];
                } else {
                    // 不选和选物品 i 这两种方案的较大值
                    dp[c] = Math.Max(dp[c], dp[c - weight[i - 1]] + val[i - 1]);
                }
            }
        }
        return dp[cap];
    }

    [Test]
    public void Test() {
        int[] weight = { 10, 20, 30, 40, 50 };
        int[] val = { 50, 120, 150, 210, 240 };
        int cap = 50;
        int n = weight.Length;

        // 暴力搜索
        int res = knapsackDFS(weight, val, n, cap);
        Console.WriteLine("不超过背包容量的最大物品价值为 " + res);

        // 记忆化搜索
        int[][] mem = new int[n + 1][];
        for (int i = 0; i <= n; i++) {
            mem[i] = new int[cap + 1];
            Array.Fill(mem[i], -1);
        }
        res = knapsackDFSMem(weight, val, mem, n, cap);
        Console.WriteLine("不超过背包容量的最大物品价值为 " + res);

        // 动态规划
        res = knapsackDP(weight, val, cap);
        Console.WriteLine("不超过背包容量的最大物品价值为 " + res);

        // 空间优化后的动态规划
        res = knapsackDPComp(weight, val, cap);
        Console.WriteLine("不超过背包容量的最大物品价值为 " + res);
    }
}

🔎5.完全背包问题

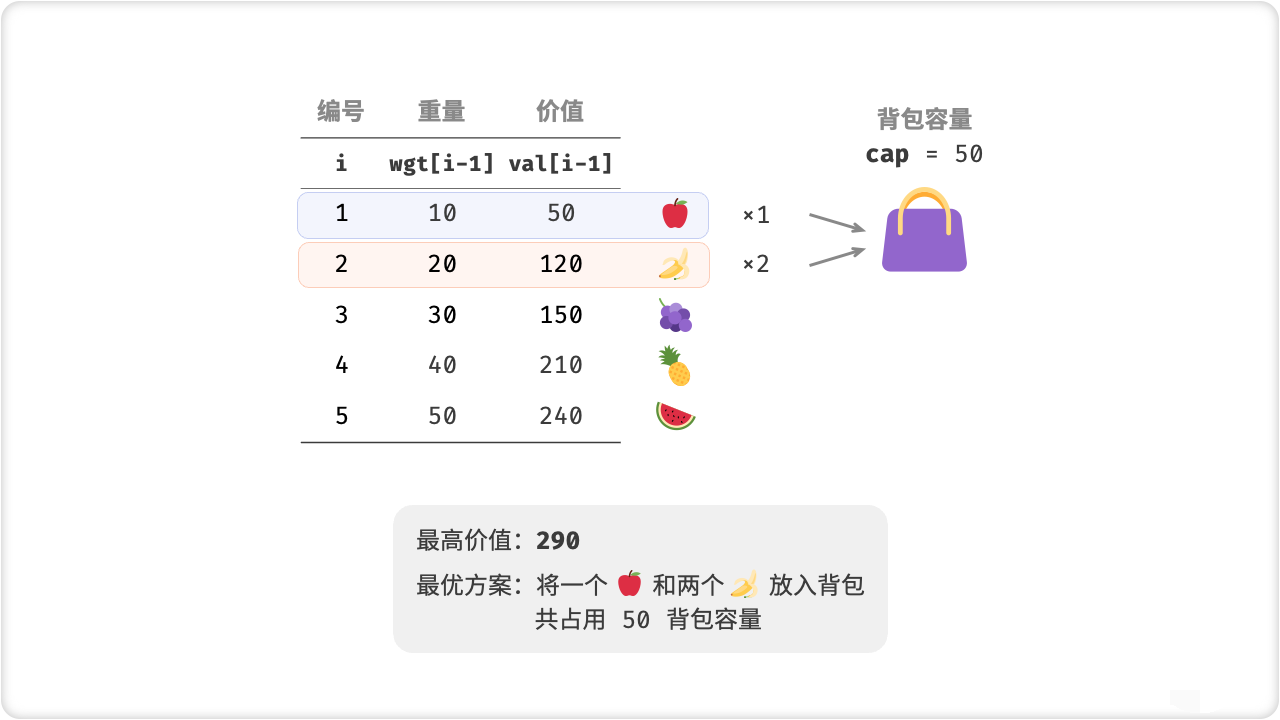
🦋5.1 完全背包

完全背包问题是指有一个容量为V的背包，和一些物品，每个物品的重量为w_i，价值为v_i。现在需要选择一些物品放入背包中，使得在不超过背包容量的前提下，背包中物品的总价值最大。

可以使用动态规划算法解决完全背包问题。具体步骤如下：

1. 定义状态：定义dp[i][j]表示前i个物品放入容量为j的背包中所得到的最大价值。

2. 定义状态转移方程：对于第i个物品，有两种情况：放入背包或不放入背包。如果放入背包，则背包中的总价值为dp[i][j-w[i]] + v[i]，即前i个物品放入容量为j-w[i]的背包中所得到的最大价值加上第i个物品的价值v[i]。如果不放入背包，则背包中的总价值为dp[i-1][j]，即前i-1个物品放入容量为j的背包中所得到的最大价值。综合两种情况，状态转移方程为dp[i][j] = max(dp[i][j-w[i]] + v[i], dp[i-1][j])。

3. 初始化：dp[0][j] = 0，表示前0个物品放入容量为j的背包中所得到的最大价值为0。

4. 计算结果：最终结果为dp[n][V]，其中n为物品的个数，V为背包的容量。

完全背包问题与01背包问题和多重背包问题不同，01背包问题中每个物品只能选择放或不放，而多重背包问题中每个物品有一定数量限制。而在完全背包问题中，每个物品可以无限制地选择放入背包中。

public class unbounded_knapsack {
    /* 完全背包：动态规划 */
    public int unboundedKnapsackDP(int[] wgt, int[] val, int cap) {
        int n = wgt.Length;
        // 初始化 dp 表
        int[,] dp = new int[n + 1, cap + 1];
        // 状态转移
        for (int i = 1; i <= n; i++) {
            for (int c = 1; c <= cap; c++) {
                if (wgt[i - 1] > c) {
                    // 若超过背包容量，则不选物品 i
                    dp[i, c] = dp[i - 1, c];
                } else {
                    // 不选和选物品 i 这两种方案的较大值
                    dp[i, c] = Math.Max(dp[i - 1, c], dp[i, c - wgt[i - 1]] + val[i - 1]);
                }
            }
        }
        return dp[n, cap];
    }

    /* 完全背包：空间优化后的动态规划 */
    public int unboundedKnapsackDPComp(int[] wgt, int[] val, int cap) {
        int n = wgt.Length;
        // 初始化 dp 表
        int[] dp = new int[cap + 1];
        // 状态转移
        for (int i = 1; i <= n; i++) {
            for (int c = 1; c <= cap; c++) {
                if (wgt[i - 1] > c) {
                    // 若超过背包容量，则不选物品 i
                    dp[c] = dp[c];
                } else {
                    // 不选和选物品 i 这两种方案的较大值
                    dp[c] = Math.Max(dp[c], dp[c - wgt[i - 1]] + val[i - 1]);
                }
            }
        }
        return dp[cap];
    }

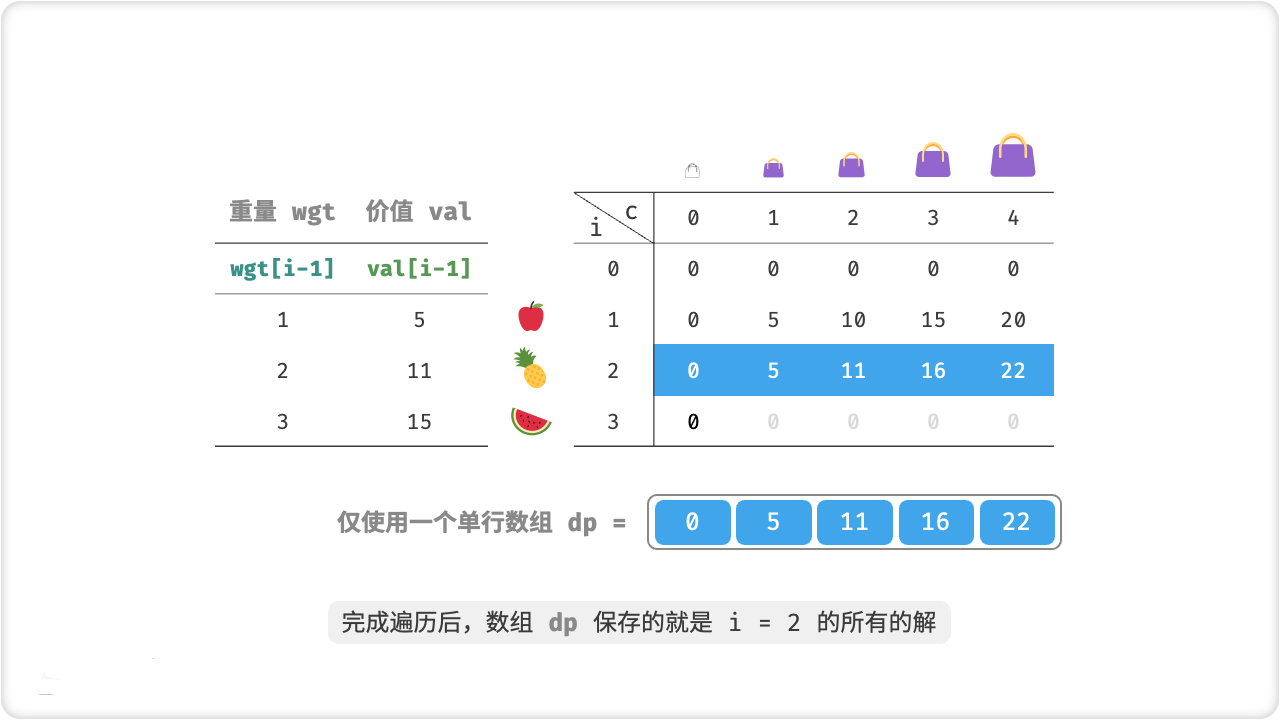
    [Test]
    public void Test() {
        int[] wgt = { 1, 2, 3 };
        int[] val = { 5, 11, 15 };
        int cap = 4;

        // 动态规划
        int res = unboundedKnapsackDP(wgt, val, cap);
        Console.WriteLine("不超过背包容量的最大物品价值为 " + res);

        // 空间优化后的动态规划
        res = unboundedKnapsackDPComp(wgt, val, cap);
        Console.WriteLine("不超过背包容量的最大物品价值为 " + res);
    }
}

🦋5.2 零钱兑换问题

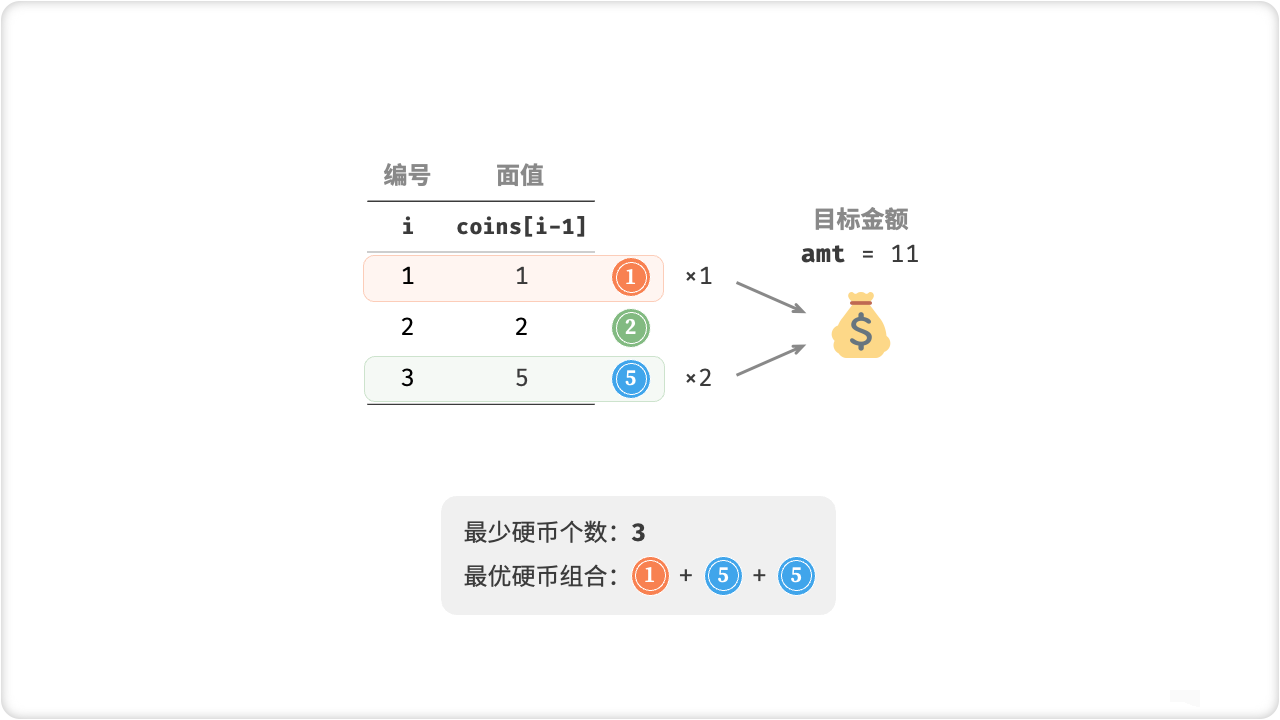
给定 (n) 种硬币，第 (i) 种硬币的面值为 (coins[i - 1]) ，目标金额为 (amt) ，每种硬币可以重复选取，问能够凑出目标金额的最少硬币个数。如果无法凑出目标金额则返回 (-1) 。

public class coin_change {
    /* 零钱兑换：动态规划 */
    public int coinChangeDP(int[] coins, int amt) {
        int n = coins.Length;
        int MAX = amt + 1;
        // 初始化 dp 表
        int[,] dp = new int[n + 1, amt + 1];
        // 状态转移：首行首列
        for (int a = 1; a <= amt; a++) {
            dp[0, a] = MAX;
        }
        // 状态转移：其余行列
        for (int i = 1; i <= n; i++) {
            for (int a = 1; a <= amt; a++) {
                if (coins[i - 1] > a) {
                    // 若超过背包容量，则不选硬币 i
                    dp[i, a] = dp[i - 1, a];
                } else {
                    // 不选和选硬币 i 这两种方案的较小值
                    dp[i, a] = Math.Min(dp[i - 1, a], dp[i, a - coins[i - 1]] + 1);
                }
            }
        }
        return dp[n, amt] != MAX ? dp[n, amt] : -1;
    }

    /* 零钱兑换：空间优化后的动态规划 */
    public int coinChangeDPComp(int[] coins, int amt) {
        int n = coins.Length;
        int MAX = amt + 1;
        // 初始化 dp 表
        int[] dp = new int[amt + 1];
        Array.Fill(dp, MAX);
        dp[0] = 0;
        // 状态转移
        for (int i = 1; i <= n; i++) {
            for (int a = 1; a <= amt; a++) {
                if (coins[i - 1] > a) {
                    // 若超过背包容量，则不选硬币 i
                    dp[a] = dp[a];
                } else {
                    // 不选和选硬币 i 这两种方案的较小值
                    dp[a] = Math.Min(dp[a], dp[a - coins[i - 1]] + 1);
                }
            }
        }
        return dp[amt] != MAX ? dp[amt] : -1;
    }

    [Test]
    public void Test() {
        int[] coins = { 1, 2, 5 };
        int amt = 4;

        // 动态规划
        int res = coinChangeDP(coins, amt);
        Console.WriteLine("凑到目标金额所需的最少硬币数量为 " + res);

        // 空间优化后的动态规划
        res = coinChangeDPComp(coins, amt);
        Console.WriteLine("凑到目标金额所需的最少硬币数量为 " + res);
    }
}

🦋5.3 零钱兑换问题 II

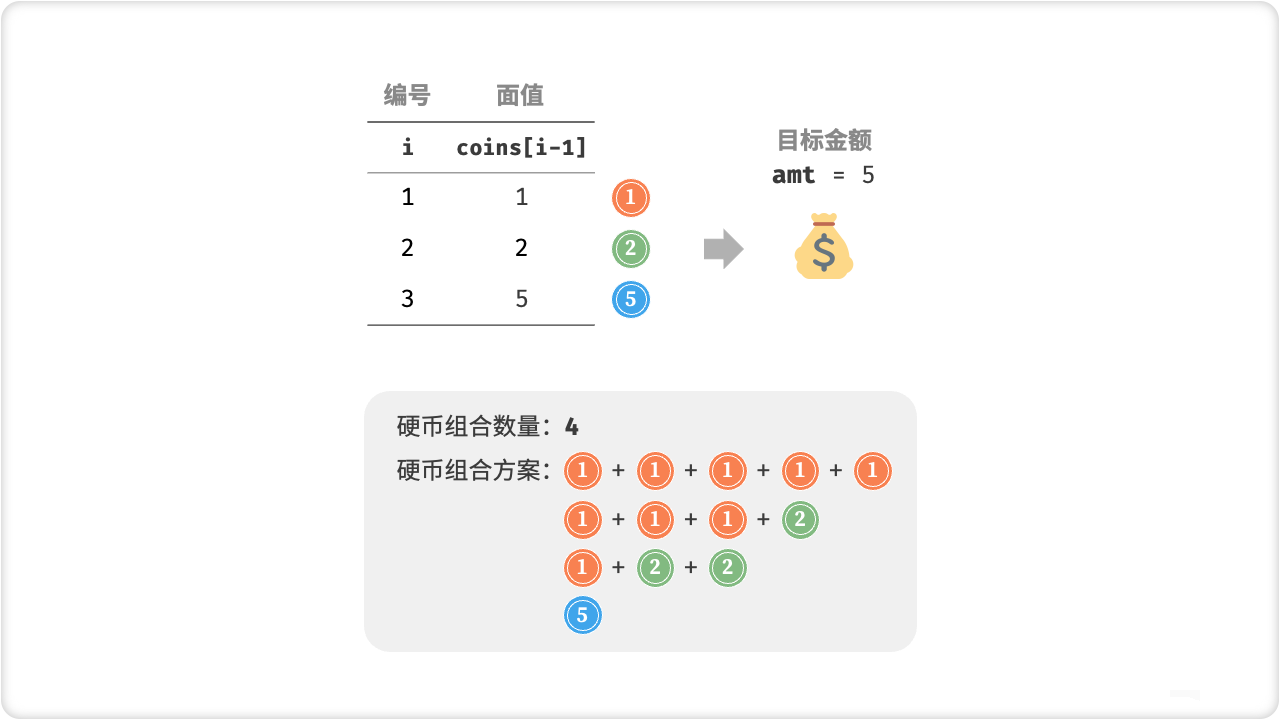
给定 (n) 种硬币，第 (i) 种硬币的面值为 (coins[i - 1]) ，目标金额为 (amt) ，每种硬币可以重复选取，问在凑出目标金额的硬币组合数量。

public class coin_change_ii {
    /* 零钱兑换 II：动态规划 */
    public int coinChangeIIDP(int[] coins, int amt) {
        int n = coins.Length;
        // 初始化 dp 表
        int[,] dp = new int[n + 1, amt + 1];
        // 初始化首列
        for (int i = 0; i <= n; i++) {
            dp[i, 0] = 1;
        }
        // 状态转移
        for (int i = 1; i <= n; i++) {
            for (int a = 1; a <= amt; a++) {
                if (coins[i - 1] > a) {
                    // 若超过背包容量，则不选硬币 i
                    dp[i, a] = dp[i - 1, a];
                } else {
                    // 不选和选硬币 i 这两种方案之和
                    dp[i, a] = dp[i - 1, a] + dp[i, a - coins[i - 1]];
                }
            }
        }
        return dp[n, amt];
    }

    /* 零钱兑换 II：空间优化后的动态规划 */
    public int coinChangeIIDPComp(int[] coins, int amt) {
        int n = coins.Length;
        // 初始化 dp 表
        int[] dp = new int[amt + 1];
        dp[0] = 1;
        // 状态转移
        for (int i = 1; i <= n; i++) {
            for (int a = 1; a <= amt; a++) {
                if (coins[i - 1] > a) {
                    // 若超过背包容量，则不选硬币 i
                    dp[a] = dp[a];
                } else {
                    // 不选和选硬币 i 这两种方案之和
                    dp[a] = dp[a] + dp[a - coins[i - 1]];
                }
            }
        }
        return dp[amt];
    }

    [Test]
    public void Test() {
        int[] coins = { 1, 2, 5 };
        int amt = 5;

        // 动态规划
        int res = coinChangeIIDP(coins, amt);
        Console.WriteLine("凑出目标金额的硬币组合数量为 " + res);

        // 空间优化后的动态规划
        res = coinChangeIIDPComp(coins, amt);
        Console.WriteLine("凑出目标金额的硬币组合数量为 " + res);
    }
}

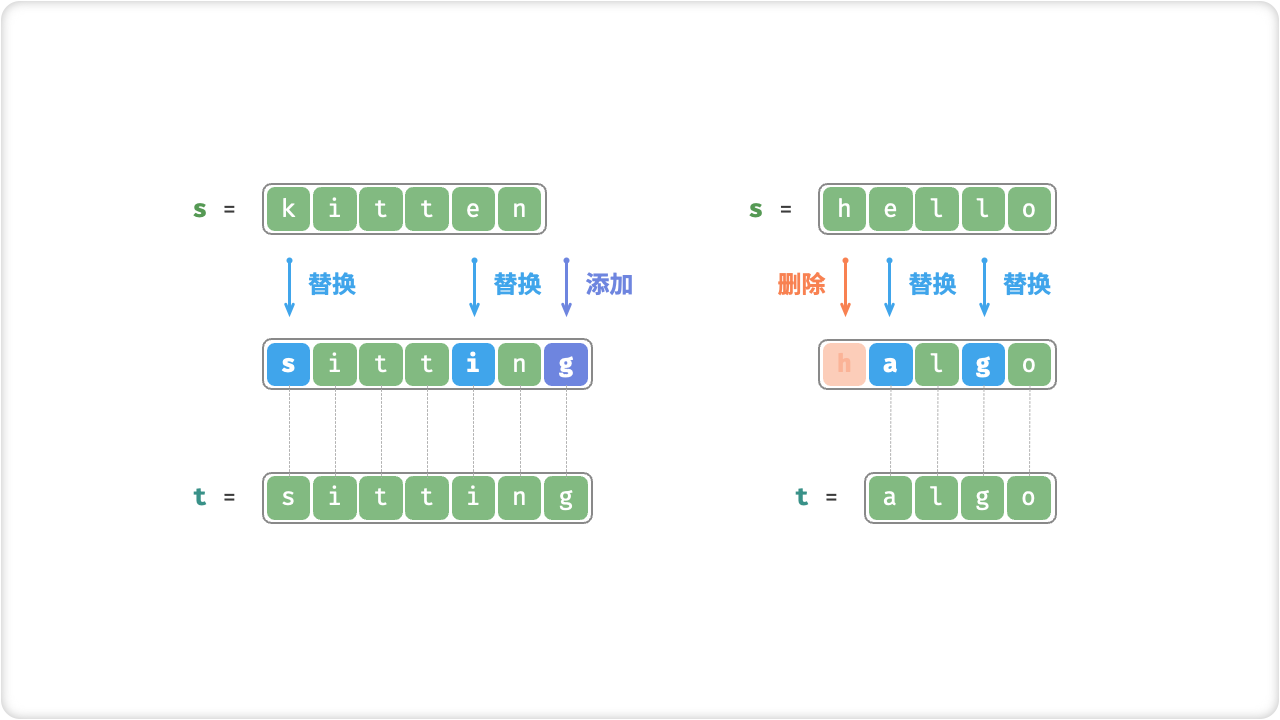
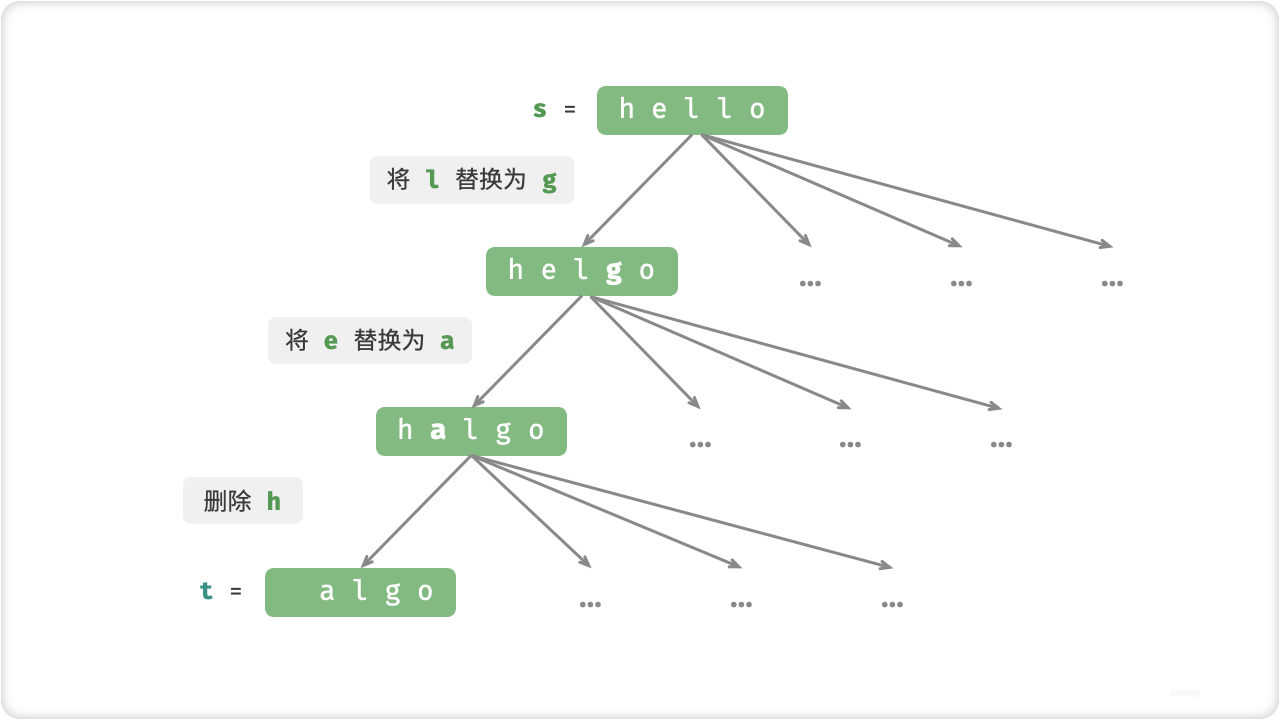
🔎6.编辑距离问题

编辑距离问题是指将一个字符串转化为另一个字符串所需的最少编辑操作数。编辑操作包括插入字符、删除字符、替换字符。动态规划算法可以解决这个问题。

假设有两个字符串s1和s2，它们的长度分别为m和n。令dp[i][j]表示将s1的前i个字符转化为s2的前j个字符所需的最少编辑操作数。考虑s1和s2的第i个字符和第j个字符是否一致：

1. 如果s1[i] == s2[j]，那么不需要编辑操作，dp[i][j] = dp[i-1][j-1]。
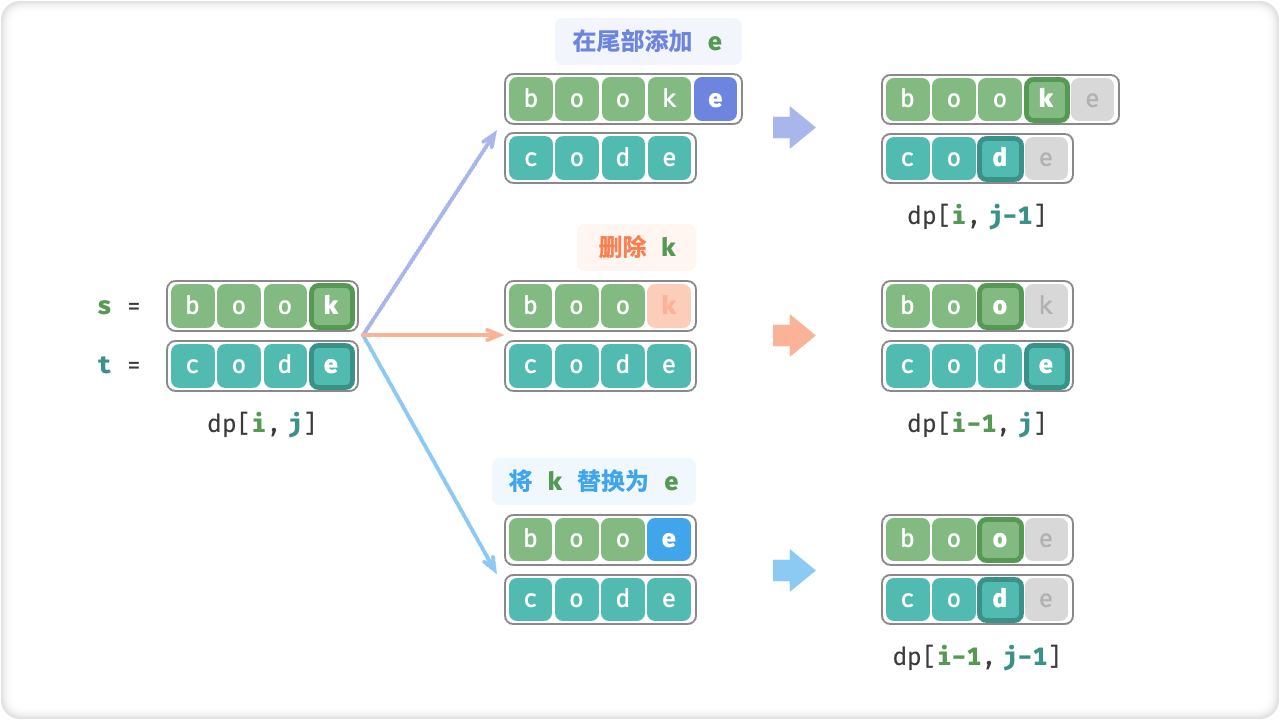
2. 如果s1[i] != s2[j]，那么有三种操作：
   a. 替换：将s1[i]替换为s2[j]，此时dp[i][j] = dp[i-1][j-1] + 1。
   b. 插入：在s1的第i个字符后插入一个字符，此时dp[i][j] = dp[i][j-1] + 1。
   c. 删除：删除s1的第i个字符，此时dp[i][j] = dp[i-1][j] + 1。

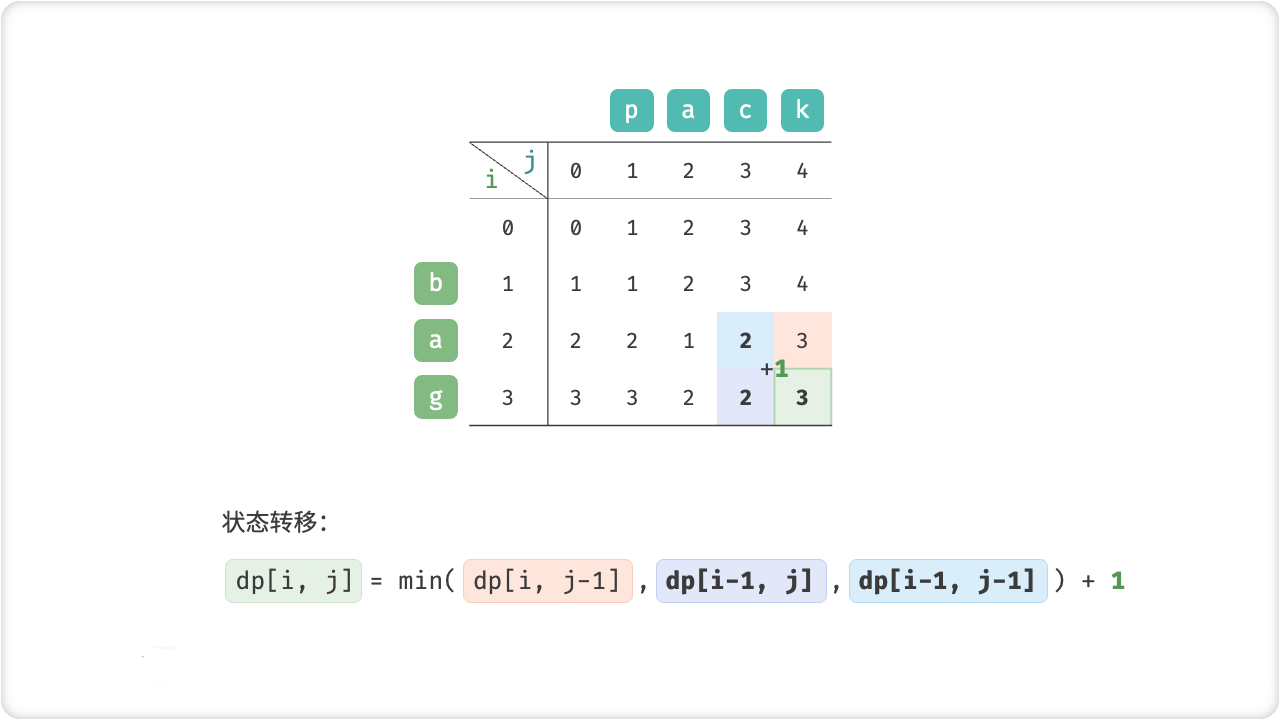
综上所述，可以得到如下的状态转移方程：

dp[i][j] = {
dp[i-1][j-1], s1[i] == s2[j]
min(dp[i-1][j-1], dp[i][j-1], dp[i-1][j]) + 1, s1[i] != s2[j]
}

其中，dp[0][0] = 0，表示将空串转化为空串不需要任何操作。最终答案为dp[m][n]。

时间复杂度为O(mn)，空间复杂度为O(mn)。可以通过滚动数组优化空间复杂度为O(min(m,n))。

public class edit_distance {
    /* 编辑距离：暴力搜索 */
    public int editDistanceDFS(string s, string t, int i, int j) {
        // 若 s 和 t 都为空，则返回 0
        if (i == 0 && j == 0)
            return 0;
        // 若 s 为空，则返回 t 长度
        if (i == 0)
            return j;
        // 若 t 为空，则返回 s 长度
        if (j == 0)
            return i;
        // 若两字符相等，则直接跳过此两字符
        if (s[i - 1] == t[j - 1])
            return editDistanceDFS(s, t, i - 1, j - 1);
        // 最少编辑步数 = 插入、删除、替换这三种操作的最少编辑步数 + 1
        int insert = editDistanceDFS(s, t, i, j - 1);
        int delete = editDistanceDFS(s, t, i - 1, j);
        int replace = editDistanceDFS(s, t, i - 1, j - 1);
        // 返回最少编辑步数
        return Math.Min(Math.Min(insert, delete), replace) + 1;
    }

    /* 编辑距离：记忆化搜索 */
    public int editDistanceDFSMem(string s, string t, int[][] mem, int i, int j) {
        // 若 s 和 t 都为空，则返回 0
        if (i == 0 && j == 0)
            return 0;
        // 若 s 为空，则返回 t 长度
        if (i == 0)
            return j;
        // 若 t 为空，则返回 s 长度
        if (j == 0)
            return i;
        // 若已有记录，则直接返回之
        if (mem[i][j] != -1)
            return mem[i][j];
        // 若两字符相等，则直接跳过此两字符
        if (s[i - 1] == t[j - 1])
            return editDistanceDFSMem(s, t, mem, i - 1, j - 1);
        // 最少编辑步数 = 插入、删除、替换这三种操作的最少编辑步数 + 1
        int insert = editDistanceDFSMem(s, t, mem, i, j - 1);
        int delete = editDistanceDFSMem(s, t, mem, i - 1, j);
        int replace = editDistanceDFSMem(s, t, mem, i - 1, j - 1);
        // 记录并返回最少编辑步数
        mem[i][j] = Math.Min(Math.Min(insert, delete), replace) + 1;
        return mem[i][j];
    }

    /* 编辑距离：动态规划 */
    public int editDistanceDP(string s, string t) {
        int n = s.Length, m = t.Length;
        int[,] dp = new int[n + 1, m + 1];
        // 状态转移：首行首列
        for (int i = 1; i <= n; i++) {
            dp[i, 0] = i;
        }
        for (int j = 1; j <= m; j++) {
            dp[0, j] = j;
        }
        // 状态转移：其余行列
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if (s[i - 1] == t[j - 1]) {
                    // 若两字符相等，则直接跳过此两字符
                    dp[i, j] = dp[i - 1, j - 1];
                } else {
                    // 最少编辑步数 = 插入、删除、替换这三种操作的最少编辑步数 + 1
                    dp[i, j] = Math.Min(Math.Min(dp[i, j - 1], dp[i - 1, j]), dp[i - 1, j - 1]) + 1;
                }
            }
        }
        return dp[n, m];
    }

    /* 编辑距离：空间优化后的动态规划 */
    public int editDistanceDPComp(string s, string t) {
        int n = s.Length, m = t.Length;
        int[] dp = new int[m + 1];
        // 状态转移：首行
        for (int j = 1; j <= m; j++) {
            dp[j] = j;
        }
        // 状态转移：其余行
        for (int i = 1; i <= n; i++) {
            // 状态转移：首列
            int leftup = dp[0]; // 暂存 dp[i-1, j-1]
            dp[0] = i;
            // 状态转移：其余列
            for (int j = 1; j <= m; j++) {
                int temp = dp[j];
                if (s[i - 1] == t[j - 1]) {
                    // 若两字符相等，则直接跳过此两字符
                    dp[j] = leftup;
                } else {
                    // 最少编辑步数 = 插入、删除、替换这三种操作的最少编辑步数 + 1
                    dp[j] = Math.Min(Math.Min(dp[j - 1], dp[j]), leftup) + 1;
                }
                leftup = temp; // 更新为下一轮的 dp[i-1, j-1]
            }
        }
        return dp[m];
    }

    [Test]
    public void Test() {
        string s = "bag";
        string t = "pack";
        int n = s.Length, m = t.Length;

        // 暴力搜索
        int res = editDistanceDFS(s, t, n, m);
        Console.WriteLine("将 " + s + " 更改为 " + t + " 最少需要编辑 " + res + " 步");

        // 记忆化搜索
        int[][] mem = new int[n + 1][];
        for (int i = 0; i <= n; i++) {
            mem[i] = new int[m + 1];
            Array.Fill(mem[i], -1);
        }

        res = editDistanceDFSMem(s, t, mem, n, m);
        Console.WriteLine("将 " + s + " 更改为 " + t + " 最少需要编辑 " + res + " 步");

        // 动态规划
        res = editDistanceDP(s, t);
        Console.WriteLine("将 " + s + " 更改为 " + t + " 最少需要编辑 " + res + " 步");

        // 空间优化后的动态规划
        res = editDistanceDPComp(s, t);
        Console.WriteLine("将 " + s + " 更改为 " + t + " 最少需要编辑 " + res + " 步");
    }
}

🚀感谢：给读者的一封信

亲爱的读者，

我在这篇文章中投入了大量的心血和时间，希望为您提供有价值的内容。这篇文章包含了深入的研究和个人经验，我相信这些信息对您非常有帮助。

如果您觉得这篇文章对您有所帮助，我诚恳地请求您考虑赞赏1元钱的支持。这个金额不会对您的财务状况造成负担，但它会对我继续创作高质量的内容产生积极的影响。

我之所以写这篇文章，是因为我热爱分享有用的知识和见解。您的支持将帮助我继续这个使命，也鼓励我花更多的时间和精力创作更多有价值的内容。

如果您愿意支持我的创作，请扫描下面二维码，您的支持将不胜感激。同时，如果您有任何反馈或建议，也欢迎与我分享。

再次感谢您的阅读和支持！

最诚挚的问候， “愚公搬代码”