【愚公系列】2023年12月 五大常用算法(二)-回溯算法
🏆 作者简介,愚公搬代码
🏆《头衔》:华为云特约编辑,华为云云享专家,华为开发者专家,华为产品云测专家,CSDN博客专家,阿里云专家博主,腾讯云优秀博主,掘金优秀博主,51CTO博客专家等。
🏆《近期荣誉》:2022年CSDN博客之星TOP2,2022年华为云十佳博主等。
🏆《博客内容》:.NET、Java、Python、Go、Node、前端、IOS、Android、鸿蒙、Linux、物联网、网络安全、大数据、人工智能、U3D游戏、小程序等相关领域知识。
🏆🎉欢迎 👍点赞✍评论⭐收藏
🚀前言
五大常用算法的特点如下:
-
分治:将一个大问题拆分成若干个小问题,分别解决,然后将解决结果合并起来得到整个问题的解。分治算法的特点是递归,效率高,但对数据的规律要求比较高,需要较高的算法设计技巧。常见应用领域为排序、查找和统计等。
-
动态规划:将一个大问题分解成若干个小问题,通过寻找子问题之间的递推关系,求解小问题的最优解,然后将小问题的最优解组合起来解决整个大问题。动态规划的特点是可以解决具有重叠子问题的问题,但需要较高的时间和空间复杂度。常见应用领域为求解最大子序列、背包问题等。
-
贪心:在处理问题的过程中,每次做出局部最优的选择,希望通过局部最优的选择达到全局最优。贪心算法的特点是快速、简单,但是无法保证每个局部最优解会导致全局最优解。常见应用领域为最小生成树、活动安排等。
-
回溯:通过不断尝试局部的解,如果不满足要求就回溯返回,直到找到解为止。回溯算法的特点是可以解决多种类型的问题,但需要搜索所有可能的解,时间复杂度较高。常见应用领域为八皇后问题、排列组合问题等。
-
分支限界:与回溯算法相似,但是在搜索的过程中,通过剪枝操作来减少搜索的空间,提高算法效率。常见应用领域为旅行商问题、图着色问题等。
🚀一、回溯算法
🔎1.基本思想
回溯算法的基本思想是在搜索过程中,对每个可能的步骤都尝试一遍,如果该步骤不行,则回溯到上一步,尝试其他可能的步骤,直到找到解决问题的方案。回溯算法通常用于解决搜索和优化问题,如数独游戏、全排列、组合、子集、棋盘问题等。
回溯算法的流程通常如下:
- 选择当前可选的一个路径。
- 对于当前路径进行搜索,如果路径达到了终止状态,则达到了结果。
- 如果路径不能到达终止状态,则返回上一个路径,即回溯,尝试其他可选路径。
- 重复步骤1至3,直到找到结果或者所有路径都尝试完毕。
在回溯算法中,一般需要定义三个关键部分:
- 选择列表:表示当前可以做出的所有选择。
- 路径:表示当前已经做出的选择。
- 结束条件:表示已经到达了终止状态,可以结束搜索。
回溯算法的时间复杂度通常很高,因为需要枚举所有可能的情况。因此,在实际应用中,通常需要通过剪枝等技巧来优化算法效率。
/**
* File: preorder_traversal_i_compact.cs
* Created Time: 2023-04-17
* Author: hpstory (hpstory1024@163.com)
*/
namespace hello_algo.chapter_backtracking;
public class preorder_traversal_i_compact {
static List<TreeNode> res;
/* 前序遍历:例题一 */
static void preOrder(TreeNode root) {
if (root == null) {
return;
}
if (root.val == 7) {
// 记录解
res.Add(root);
}
preOrder(root.left);
preOrder(root.right);
}
[Test]
public void Test() {
TreeNode root = TreeNode.ListToTree(new List<int?> { 1, 7, 3, 4, 5, 6, 7 });
Console.WriteLine("\n初始化二叉树");
PrintUtil.PrintTree(root);
// 前序遍历
res = new List<TreeNode>();
preOrder(root);
Console.WriteLine("\n输出所有值为 7 的节点");
PrintUtil.PrintList(res.Select(p => p.val).ToList());
}
}

🦋1.1 尝试与回退
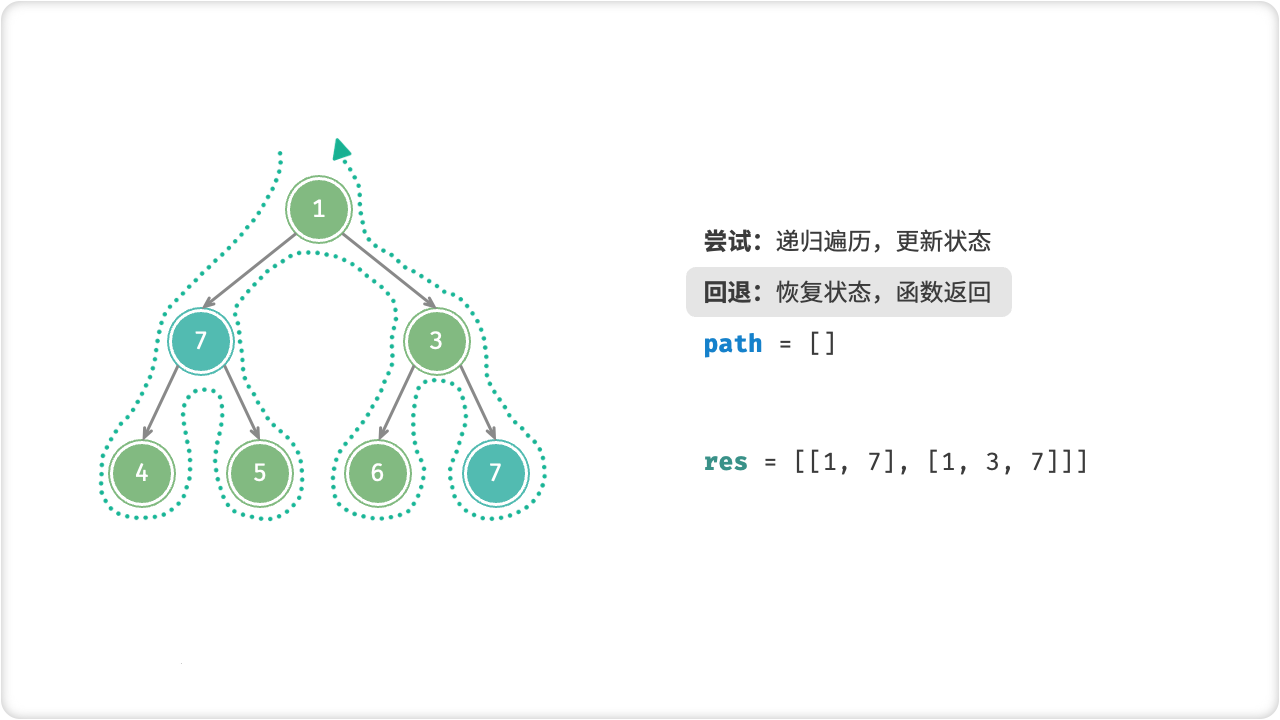
回溯算法是一种通过尝试不同的可能性来求解问题的算法。在回溯算法中,我们会从问题的起点开始,考虑所有可能的解法,每次选择一个可能的解法并前进,直到达到一个终止条件。如果到达了终止条件,则找到了一个解决方案;否则,我们需要回退到上一步,并选择另一个可能的解法,再次前进,直到找到一个解决方案或者所有的解法都被尝试过。
在回溯算法中,回退是很重要的。如果我们不回退,就会忽略掉一些可能的解法。回退操作可以让我们在选择错误的方案后,返回到之前的状态,选择另一个可能的解法。这个过程类似于在棋盘上走棋,如果一步走错了,就可以回到之前的状态,重新走一步棋。
回溯算法的关键在于如何选择可能的解法。这个过程需要根据具体的问题进行设计,对于不同的问题,可能需要不同的策略来选择解法。一般来说,回溯算法的时间复杂度比较高,因为需要尝试很多可能的解法。但是,在一些特殊情况下,回溯算法的时间复杂度可以被优化,例如使用剪枝技巧。
public class preorder_traversal_ii_compact {
static List<TreeNode> path;
static List<List<TreeNode>> res;
/* 前序遍历:例题二 */
static void preOrder(TreeNode root) {
if (root == null) {
return;
}
// 尝试
path.Add(root);
if (root.val == 7) {
// 记录解
res.Add(new List<TreeNode>(path));
}
preOrder(root.left);
preOrder(root.right);
// 回退
path.RemoveAt(path.Count - 1);
}
[Test]
public void Test() {
TreeNode root = TreeNode.ListToTree(new List<int?> { 1, 7, 3, 4, 5, 6, 7 });
Console.WriteLine("\n初始化二叉树");
PrintUtil.PrintTree(root);
// 前序遍历
path = new List<TreeNode>();
res = new List<List<TreeNode>>();
preOrder(root);
Console.WriteLine("\n输出所有根节点到节点 7 的路径");
foreach (List<TreeNode> path in res) {
PrintUtil.PrintList(path.Select(p => p.val).ToList());
}
}
}
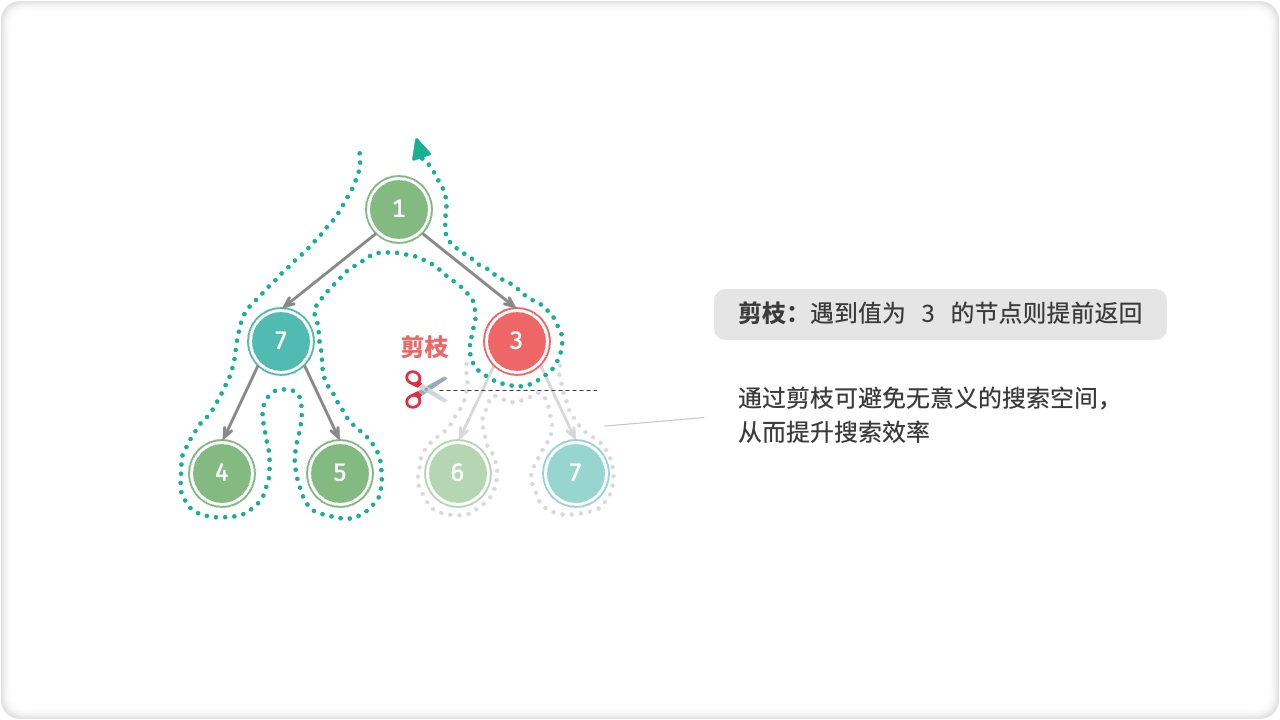
🦋1.2 剪枝
回溯算法是一种经典的搜索算法,可以用于解决很多问题,但是在搜索过程中,可能会出现无用的搜索,导致算法效率低下。因此,剪枝就是回溯算法中常用的优化方法之一,可以减少无用的搜索,从而提高算法效率。
以下是常见的回溯算法剪枝方法:
-
先排序再剪枝:在搜索前,对问题进行排序,优先搜索最有可能满足条件的情况,缩小搜索范围,减少不必要的搜索。
-
可行性剪枝:在搜索过程中,如果发现当前的状态不可能再满足条件,就直接剪枝,不继续搜索。比如,如果我们在搜索路径上的数之和已经大于目标值,就可以直接返回不继续搜索。
-
最优性剪枝:在搜索过程中,如果发现当前的状态已经不可能成为最优解,就剪枝,不继续搜索。比如,如果我们已经找到一个解并且当前解的长度已经大于已知的最短解的长度,则可以直接剪枝。
-
排除重复状态剪枝:在搜索过程中,如果发现已经搜索过相同状态,就直接剪枝,避免重复搜索。比如,在搜索一个有序数组时,如果当前数和上一个数相同,那么就可以直接剪枝。
这些剪枝方法可以结合使用,根据具体问题进行选择。剪枝可以减少搜索过程中无效的步骤,提高搜索效率,优化算法。
public class preorder_traversal_iii_compact {
static List<TreeNode> path;
static List<List<TreeNode>> res;
/* 前序遍历:例题三 */
static void preOrder(TreeNode root) {
// 剪枝
if (root == null || root.val == 3) {
return;
}
// 尝试
path.Add(root);
if (root.val == 7) {
// 记录解
res.Add(new List<TreeNode>(path));
}
preOrder(root.left);
preOrder(root.right);
// 回退
path.RemoveAt(path.Count - 1);
}
[Test]
public void Test() {
TreeNode root = TreeNode.ListToTree(new List<int?> { 1, 7, 3, 4, 5, 6, 7 });
Console.WriteLine("\n初始化二叉树");
PrintUtil.PrintTree(root);
// 前序遍历
path = new List<TreeNode>();
res = new List<List<TreeNode>>();
preOrder(root);
Console.WriteLine("\n输出所有根节点到节点 7 的路径,路径中不包含值为 3 的节点");
foreach (List<TreeNode> path in res) {
PrintUtil.PrintList(path.Select(p => p.val).ToList());
}
}
}
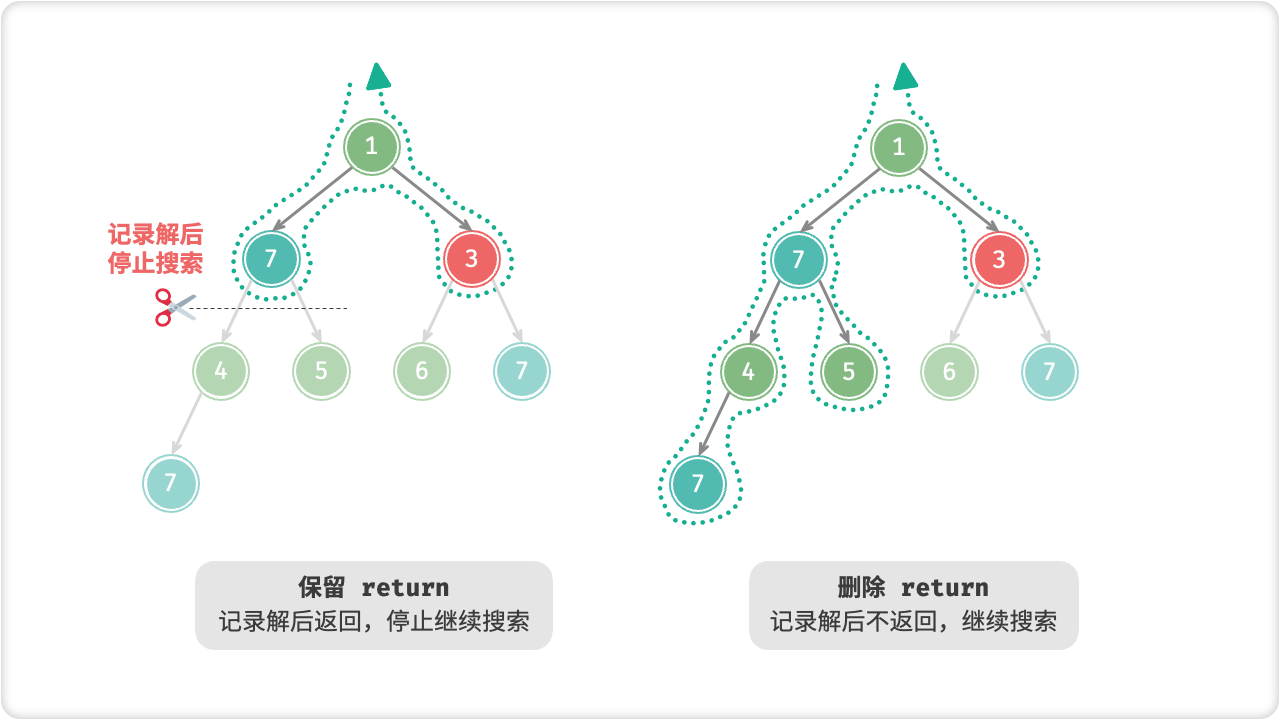
🦋1.3 框架代码
回溯的“尝试、回退、剪枝”的主体框架提炼出来进行封装如下:
/**
* File: preorder_traversal_iii_template.cs
* Created Time: 2023-04-17
* Author: hpstory (hpstory1024@163.com)
*/
namespace hello_algo.chapter_backtracking;
public class preorder_traversal_iii_template {
/* 判断当前状态是否为解 */
static bool isSolution(List<TreeNode> state) {
return state.Count != 0 && state[^1].val == 7;
}
/* 记录解 */
static void recordSolution(List<TreeNode> state, List<List<TreeNode>> res) {
res.Add(new List<TreeNode>(state));
}
/* 判断在当前状态下,该选择是否合法 */
static bool isValid(List<TreeNode> state, TreeNode choice) {
return choice != null && choice.val != 3;
}
/* 更新状态 */
static void makeChoice(List<TreeNode> state, TreeNode choice) {
state.Add(choice);
}
/* 恢复状态 */
static void undoChoice(List<TreeNode> state, TreeNode choice) {
state.RemoveAt(state.Count - 1);
}
/* 回溯算法:例题三 */
static void backtrack(List<TreeNode> state, List<TreeNode> choices, List<List<TreeNode>> res) {
// 检查是否为解
if (isSolution(state)) {
// 记录解
recordSolution(state, res);
}
// 遍历所有选择
foreach (TreeNode choice in choices) {
// 剪枝:检查选择是否合法
if (isValid(state, choice)) {
// 尝试:做出选择,更新状态
makeChoice(state, choice);
// 进行下一轮选择
backtrack(state, new List<TreeNode> { choice.left, choice.right }, res);
// 回退:撤销选择,恢复到之前的状态
undoChoice(state, choice);
}
}
}
[Test]
public void Test() {
TreeNode root = TreeNode.ListToTree(new List<int?> { 1, 7, 3, 4, 5, 6, 7 });
Console.WriteLine("\n初始化二叉树");
PrintUtil.PrintTree(root);
// 回溯算法
List<List<TreeNode>> res = new List<List<TreeNode>>();
List<TreeNode> choices = new List<TreeNode>() { root };
backtrack(new List<TreeNode>(), choices, res);
Console.WriteLine("\n输出所有根节点到节点 7 的路径,要求路径中不包含值为 3 的节点");
foreach (List<TreeNode> path in res) {
PrintUtil.PrintList(path.Select(p => p.val).ToList());
}
}
}
相比基于前序遍历的代码实现,基于回溯算法框架的代码实现虽然显得啰嗦,但通用性更好。实际上,许多回溯问题都可以在该框架下解决。我们只需根据具体问题来定义 state 和 choices ,并实现框架中的各个方法即可。
🦋1.4 常用术语
| 名词 | 定义 | 例题三 |
|---|---|---|
| 解 Solution | 解是满足问题特定条件的答案,可能有一个或多个 | 根节点到节点7的满足约束条件的所有路径 |
| 约束条件 Constraint | 约束条件是问题中限制解的可行性的条件,通常用于剪枝 | 路径中不包含节点 3 |
| 状态 State | 状态表示问题在某一时刻的情况,包括已经做出的选择 | 当前已访问的节点路径,即 path 节点列表 |
| 尝试 Attempt | 尝试是根据可用选择来探索解空间的过程,包括做出选择,更新状态,检查是否为解 | 递归访问左(右)子节点,将节点添加进 path ,判断节点的值是否为 7 |
| 回退 Backtracking | 回退指遇到不满足约束条件的状态时,撤销前面做出的选择,回到上一个状态 | 当越过叶结点、结束结点访问、遇到值为3的节点时终止搜索,函数返回 |
| 剪枝 Pruning | 剪枝是根据问题特性和约束条件避免无意义的搜索路径的方法,可提高搜索效率 | 当遇到值为3 的节点时,则终止继续搜索 |
🦋1.5 优势与局限性
回溯算法是一种通过尝试各种可能的解来解决问题的算法。它的优势在于它可以处理一些复杂的组合问题,如排列、组合、子集等。它可以在搜索树中进行剪枝来优化搜索效率,并且它的空间复杂度比较小,因为在搜索的过程中只需要保存当前状态,而不需要保存历史状态。
然而,回溯算法也有其局限性。一是它是一种暴力搜索算法,需要遍历搜索树的所有节点,时间复杂度较高,当问题规模较大时,它的效率会变得非常低下。二是它可能会出现重复解的问题。如果问题的解有重复的情况,可能会导致算法搜索的节点数增加,使得算法效率降低。因此,在实际应用中,需要对算法进行优化,减少搜索树的规模。三是它在选取候选解时必须保证候选解具有可行性,否则可能会导致算法找不到可行解的情况。
综上所述,回溯算法是一种灵活的算法,适用于一些复杂的组合问题,但也有一些局限性。在实际应用中,需要根据具体问题的特点来选择合适的算法,或者对回溯算法进行优化,以提高算法的效率。
🦋1.6 回溯典型例题
-
八皇后问题:在8×8的棋盘上放置8个皇后,使得它们互不攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
-
数独问题:给定一个9×9的数独,要求填充数字,使得每行、每列和每个3×3宫中的数字都是1到9,并且不能重复。
-
组合总和问题:给定一个无序数组和一个目标数,找出所有可能的组合,使得它们的和等于目标数。
-
单词搜索问题:给定一个二维字符数组和一个字符串,判断字符串能否在数组中被找到,要求按照上、下、左、右四个方向搜索,并且不能重复使用同一个字符。
-
全排列问题:给定一个不重复的整数数组,返回所有可能的全排列。
-
0/1背包问题:给定一些物品和一个固定大小的背包,要求选择一些物品放入背包中,使得它们的总价值最大,且不能超过背包的容量。
-
矩阵中的最长递增路径:给定一个矩阵,找到其中最长的递增路径,要求只能沿上、下、左、右四个方向移动。
-
最小路径和问题:给定一个矩阵,从左上角出发到右下角,只能向下或向右移动,找到一条路径,使得它经过的所有数字之和最小。
-
N皇后问题:在N×N的棋盘上放置N个皇后,使得它们互不攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
-
全排列 II:给定一个可能包含重复元素的整数数组,返回所有可能的全排列,要求不能有重复的排列。
🔎2.全排列问题
全排列问题是指给定一个序列,求出所有可能的排列方式。例如,对于序列 [1, 2, 3],所有的排列方式包括 [1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2] 和 [3, 2, 1]。这是一个经典的排列组合问题,在算法和编程中经常被遇到。
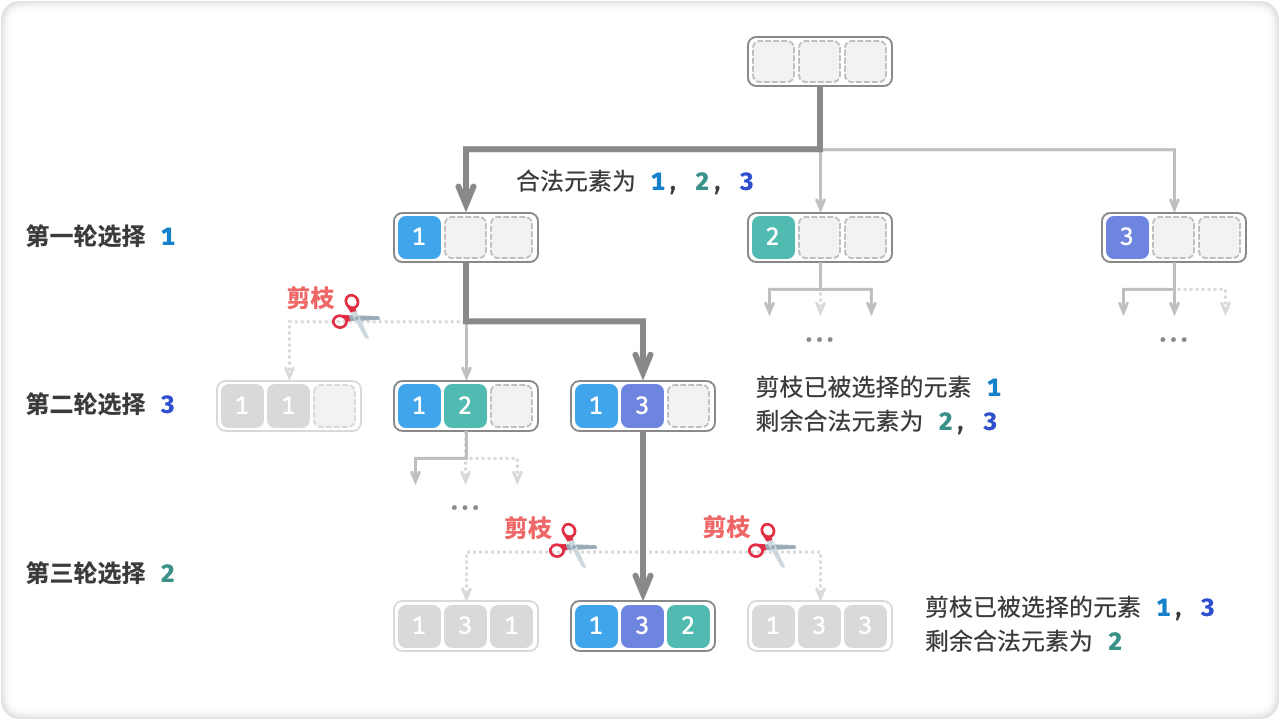
求解全排列问题的一种经典算法是回溯法。具体来说,可以从序列的第一个元素开始,依次尝试每个元素作为排列的第一个元素,然后递归求解剩下元素的排列问题。在递归过程中,需要记录已经选择过的元素,以避免重复选择。递归的退出条件是所有元素都已经被选择过,此时就可以输出一个排列结果。
🦋2.1 无相等元素的情况
全排列问题指的是对一个集合内的元素进行排列,求出所有可能的排列方式。如果集合内的元素没有重复,我们称为“无相等元素的情况”。
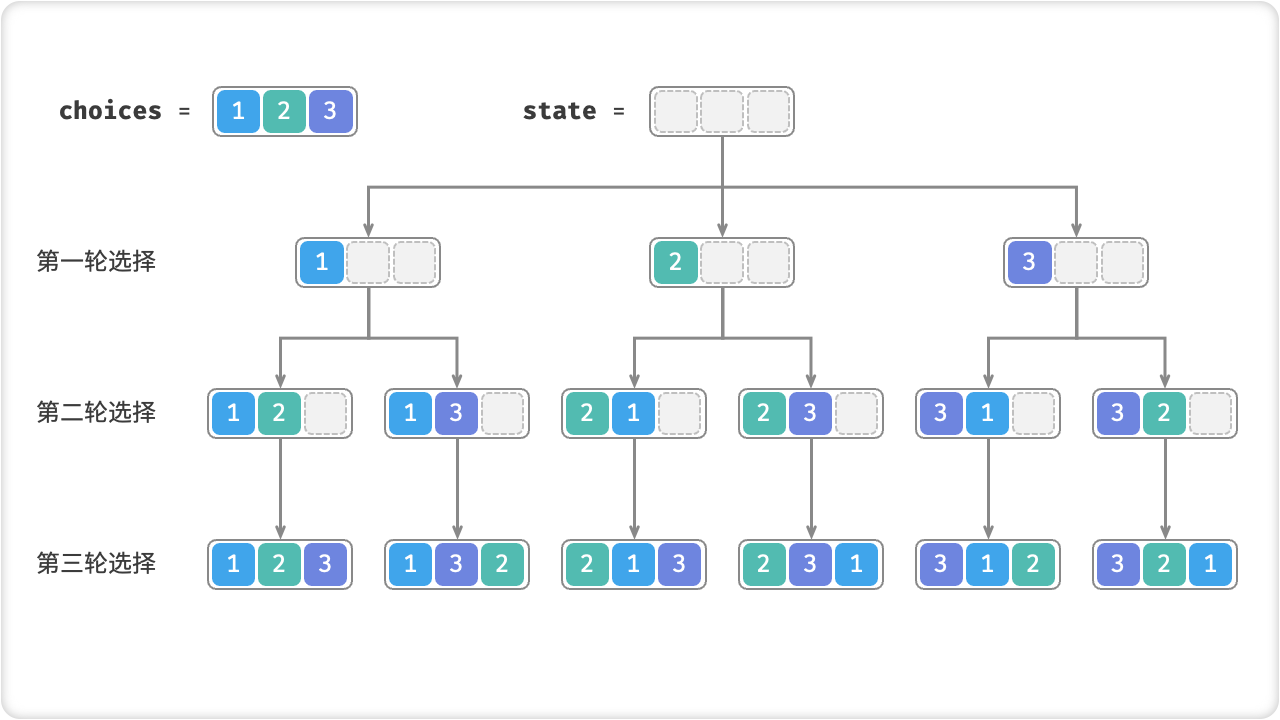
以集合 {1,2,3} 为例,它的全排列如下: {1,2,3},{1,3,2},{2,1,3},{2,3,1},{3,1,2},{3,2,1}
算法实现:
我们可以通过递归的方式实现全排列问题。首先选择第一个数,然后对剩下的数进行排列,得到剩下数的所有排列,再将第一个数与剩下数的每一个数交换,得到所有以第一个数开头的排列。接着对以第一个数开头的每一个排列做同样的操作,依次递归下去,直到最后只剩下一个数为止。
public class permutations_i {
/* 回溯算法:全排列 I */
static void backtrack(List<int> state, int[] choices, bool[] selected, List<List<int>> res) {
// 当状态长度等于元素数量时,记录解
if (state.Count == choices.Length) {
res.Add(new List<int>(state));
return;
}
// 遍历所有选择
for (int i = 0; i < choices.Length; i++) {
int choice = choices[i];
// 剪枝:不允许重复选择元素 且 不允许重复选择相等元素
if (!selected[i]) {
// 尝试:做出选择,更新状态
selected[i] = true;
state.Add(choice);
// 进行下一轮选择
backtrack(state, choices, selected, res);
// 回退:撤销选择,恢复到之前的状态
selected[i] = false;
state.RemoveAt(state.Count - 1);
}
}
}
/* 全排列 I */
static List<List<int>> permutationsI(int[] nums) {
List<List<int>> res = new List<List<int>>();
backtrack(new List<int>(), nums, new bool[nums.Length], res);
return res;
}
[Test]
public void Test() {
int[] nums = { 1, 2, 3 };
List<List<int>> res = permutationsI(nums);
Console.WriteLine("输入数组 nums = " + string.Join(", ", nums));
Console.WriteLine("所有排列 res = ");
foreach (List<int> permutation in res) {
PrintUtil.PrintList(permutation);
}
}
}
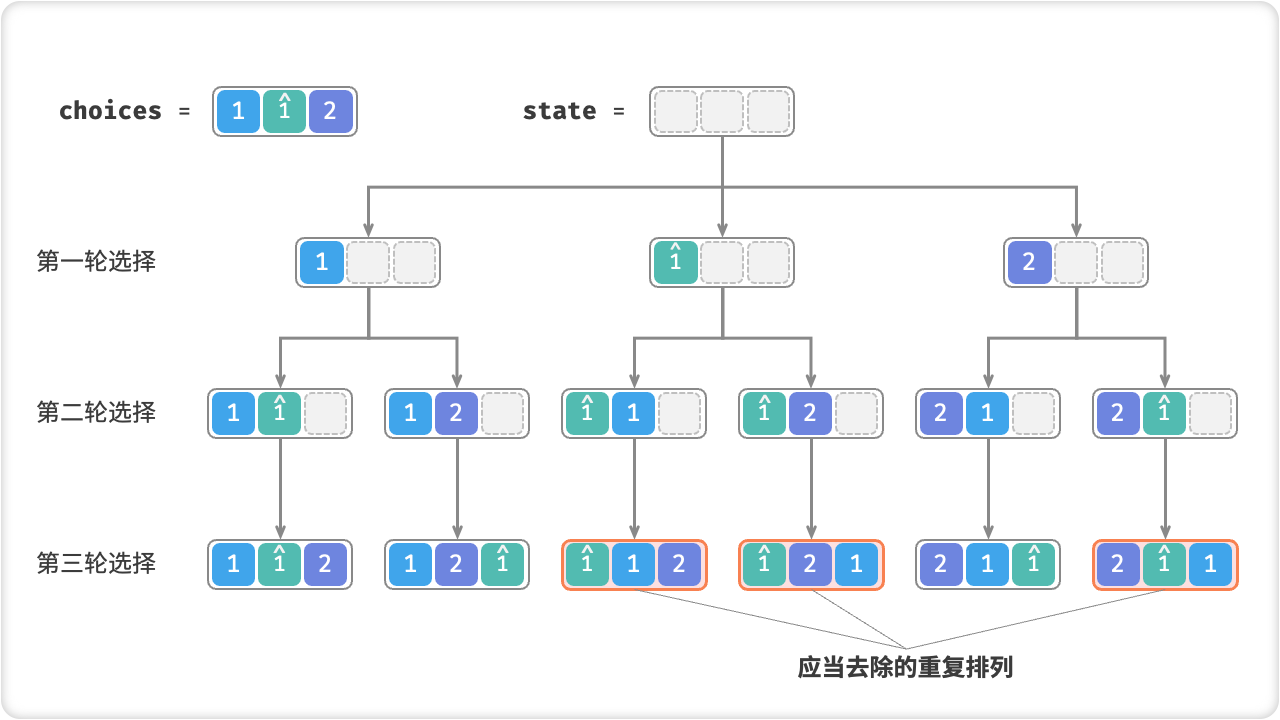
🦋2.2 有相等元素的情况
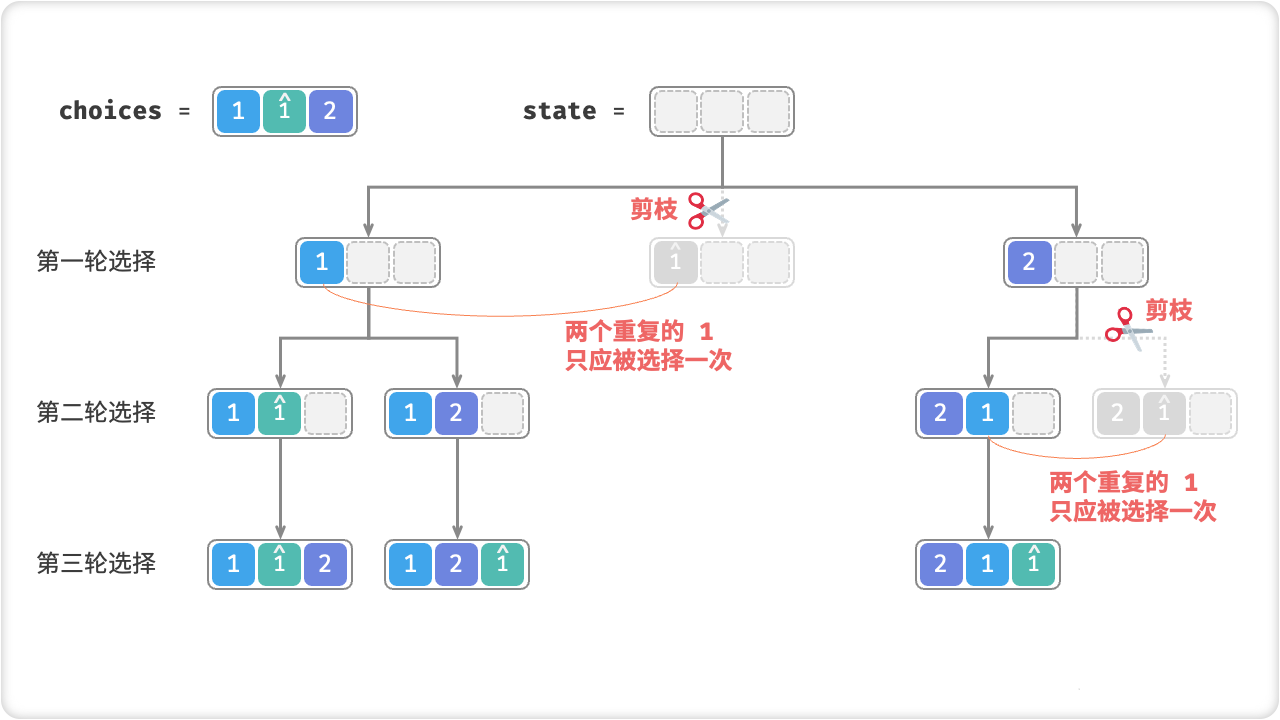
在回溯算法中,当遇到有相等元素的情况,可以通过限制重复使用相同元素的方法来避免出现重复的解。
具体来说,可以在搜索的过程中规定一个条件,例如只在当前元素与上一个元素不相等的情况下进行下一步的搜索。这样可以避免在搜索过程中出现相同元素重复放置的情况。
另外,如果需要输出所有的解,可以使用回溯算法+剪枝的思路,即在搜索过程中利用剪枝技巧避免生成重复的解,同时保留所有的解。例如可以在搜索过程中记录已经生成的解,判断当前状态是否与已有解相同,如果相同则不再进行搜索。
public class permutations_ii {
/* 回溯算法:全排列 II */
static void backtrack(List<int> state, int[] choices, bool[] selected, List<List<int>> res) {
// 当状态长度等于元素数量时,记录解
if (state.Count == choices.Length) {
res.Add(new List<int>(state));
return;
}
// 遍历所有选择
ISet<int> duplicated = new HashSet<int>();
for (int i = 0; i < choices.Length; i++) {
int choice = choices[i];
// 剪枝:不允许重复选择元素 且 不允许重复选择相等元素
if (!selected[i] && !duplicated.Contains(choice)) {
// 尝试:做出选择,更新状态
duplicated.Add(choice); // 记录选择过的元素值
selected[i] = true;
state.Add(choice);
// 进行下一轮选择
backtrack(state, choices, selected, res);
// 回退:撤销选择,恢复到之前的状态
selected[i] = false;
state.RemoveAt(state.Count - 1);
}
}
}
/* 全排列 II */
static List<List<int>> permutationsII(int[] nums) {
List<List<int>> res = new List<List<int>>();
backtrack(new List<int>(), nums, new bool[nums.Length], res);
return res;
}
[Test]
public void Test() {
int[] nums = { 1, 2, 2 };
List<List<int>> res = permutationsII(nums);
Console.WriteLine("输入数组 nums = " + string.Join(", ", nums));
Console.WriteLine("所有排列 res = ");
foreach (List<int> permutation in res) {
PrintUtil.PrintList(permutation);
}
}
}
🔎3.子集和问题
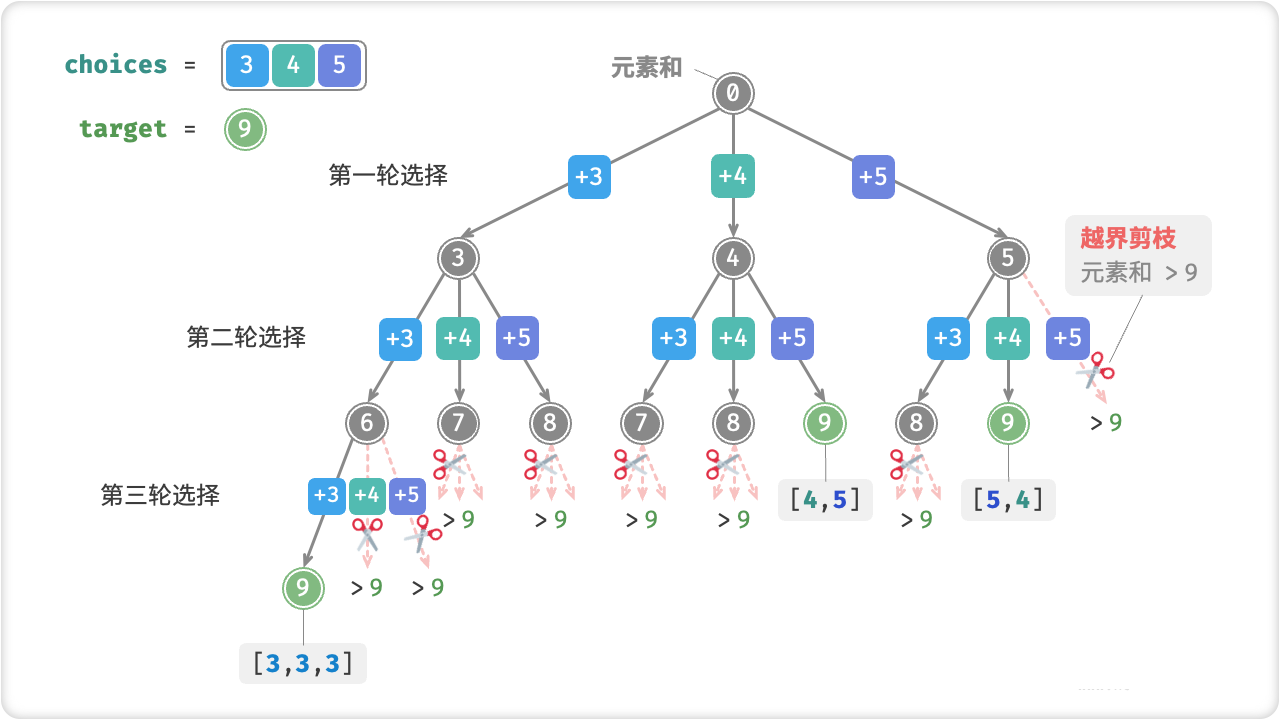
子集和问题是指给定一组正整数和一个目标数,求能否从给定的正整数中选取任意个数使其和等于目标数的问题。回溯算法可以用来解决子集和问题。例如,输入集合 ({3, 4, 5}) 和目标整数 (9) ,解为 ({3, 3, 3}, {4, 5})
回溯算法的基本思路是从一组可能的解中一步一步地逐个尝试,并在尝试过程中剪枝,以达到找到最优解的目的。在子集和问题中,回溯算法的核心是遍历所有可能的子集,对于每个子集判断其和是否等于目标数。
🦋3.1 无重复元素的情况
☀️3.1.1 全排列解法
我们可以把子集的生成过程想象成一系列选择的结果,并在选择过程中实时更新“元素和”,当元素和等于 target 时,就将子集记录至结果列表。(本题集合中的元素可以被无限次选取)
public class subset_sum_i_naive {
/* 回溯算法:子集和 I */
public static void backtrack(List<int> state, int target, int total, int[] choices, List<List<int>> res) {
// 子集和等于 target 时,记录解
if (total == target) {
res.Add(new List<int>(state));
return;
}
// 遍历所有选择
for (int i = 0; i < choices.Length; i++) {
// 剪枝:若子集和超过 target ,则跳过该选择
if (total + choices[i] > target) {
continue;
}
// 尝试:做出选择,更新元素和 total
state.Add(choices[i]);
// 进行下一轮选择
backtrack(state, target, total + choices[i], choices, res);
// 回退:撤销选择,恢复到之前的状态
state.RemoveAt(state.Count - 1);
}
}
/* 求解子集和 I(包含重复子集) */
public static List<List<int>> subsetSumINaive(int[] nums, int target) {
List<int> state = new List<int>(); // 状态(子集)
int total = 0; // 子集和
List<List<int>> res = new List<List<int>>(); // 结果列表(子集列表)
backtrack(state, target, total, nums, res);
return res;
}
[Test]
public void Test() {
int[] nums = { 3, 4, 5 };
int target = 9;
List<List<int>> res = subsetSumINaive(nums, target);
Console.WriteLine("输入数组 nums = " + string.Join(", ", nums) + ", target = " + target);
Console.WriteLine("所有和等于 " + target + " 的子集 res = ");
foreach (var subset in res) {
PrintUtil.PrintList(subset);
}
Console.WriteLine("请注意,该方法输出的结果包含重复集合");
}
}
为了去除重复子集,一种直接的思路是对结果列表进行去重。但这个方法效率很低,有两方面原因。
-
当数组元素较多,尤其是当 target 较大时,搜索过程会产生大量的重复子集。
-
比较子集(数组)的异同非常耗时,需要先排序数组,再比较数组中每个元素的异同。
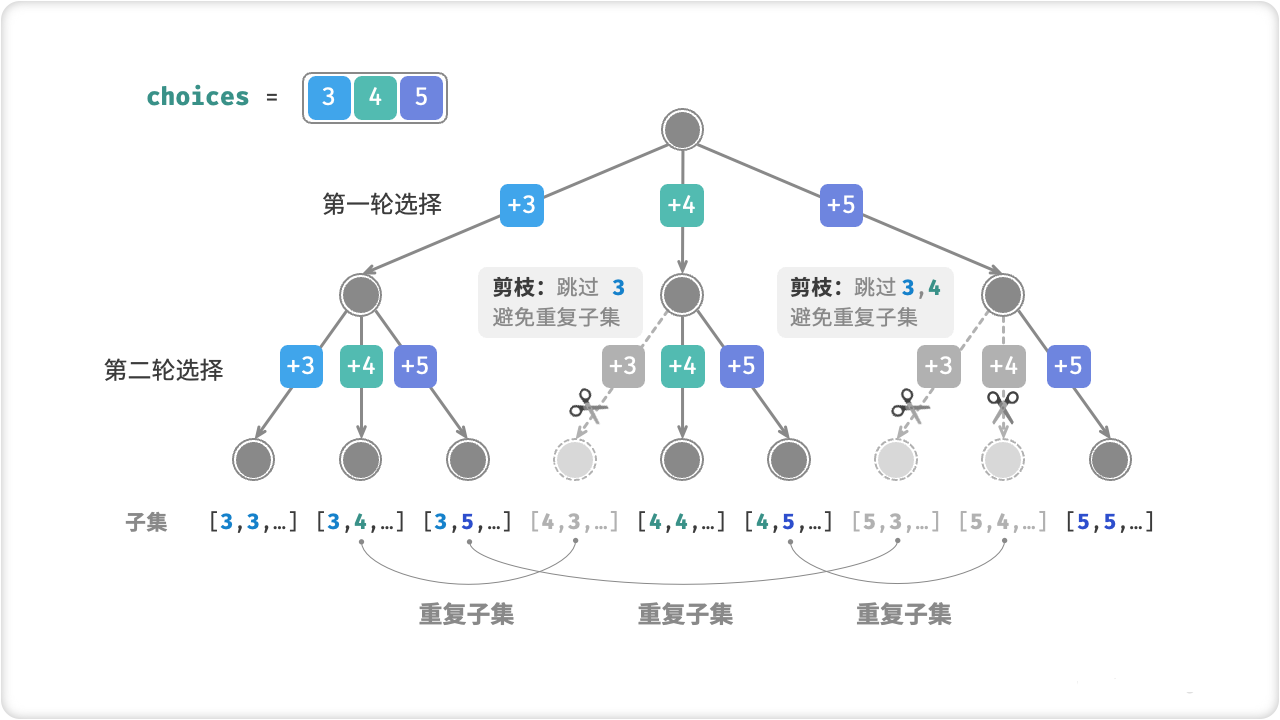
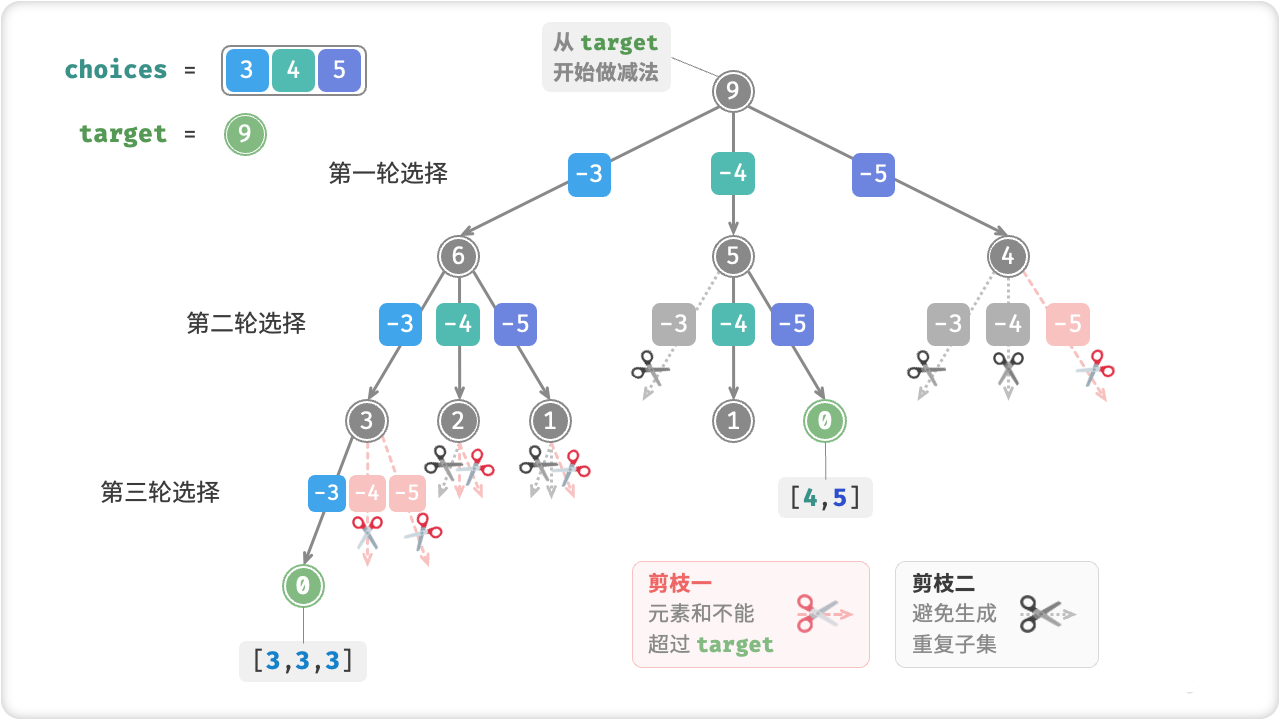
☀️3.1.2 重复子集剪枝解法
public class subset_sum_i {
/* 回溯算法:子集和 I */
public static void backtrack(List<int> state, int target, int[] choices, int start, List<List<int>> res) {
// 子集和等于 target 时,记录解
if (target == 0) {
res.Add(new List<int>(state));
return;
}
// 遍历所有选择
// 剪枝二:从 start 开始遍历,避免生成重复子集
for (int i = start; i < choices.Length; i++) {
// 剪枝一:若子集和超过 target ,则直接结束循环
// 这是因为数组已排序,后边元素更大,子集和一定超过 target
if (target - choices[i] < 0) {
break;
}
// 尝试:做出选择,更新 target, start
state.Add(choices[i]);
// 进行下一轮选择
backtrack(state, target - choices[i], choices, i, res);
// 回退:撤销选择,恢复到之前的状态
state.RemoveAt(state.Count - 1);
}
}
/* 求解子集和 I */
public static List<List<int>> subsetSumI(int[] nums, int target) {
List<int> state = new List<int>(); // 状态(子集)
Array.Sort(nums); // 对 nums 进行排序
int start = 0; // 遍历起始点
List<List<int>> res = new List<List<int>>(); // 结果列表(子集列表)
backtrack(state, target, nums, start, res);
return res;
}
[Test]
public void Test() {
int[] nums = { 3, 4, 5 };
int target = 9;
List<List<int>> res = subsetSumI(nums, target);
Console.WriteLine("输入数组 nums = " + string.Join(", ", nums) + ", target = " + target);
Console.WriteLine("所有和等于 " + target + " 的子集 res = ");
foreach (var subset in res) {
PrintUtil.PrintList(subset);
}
}
}
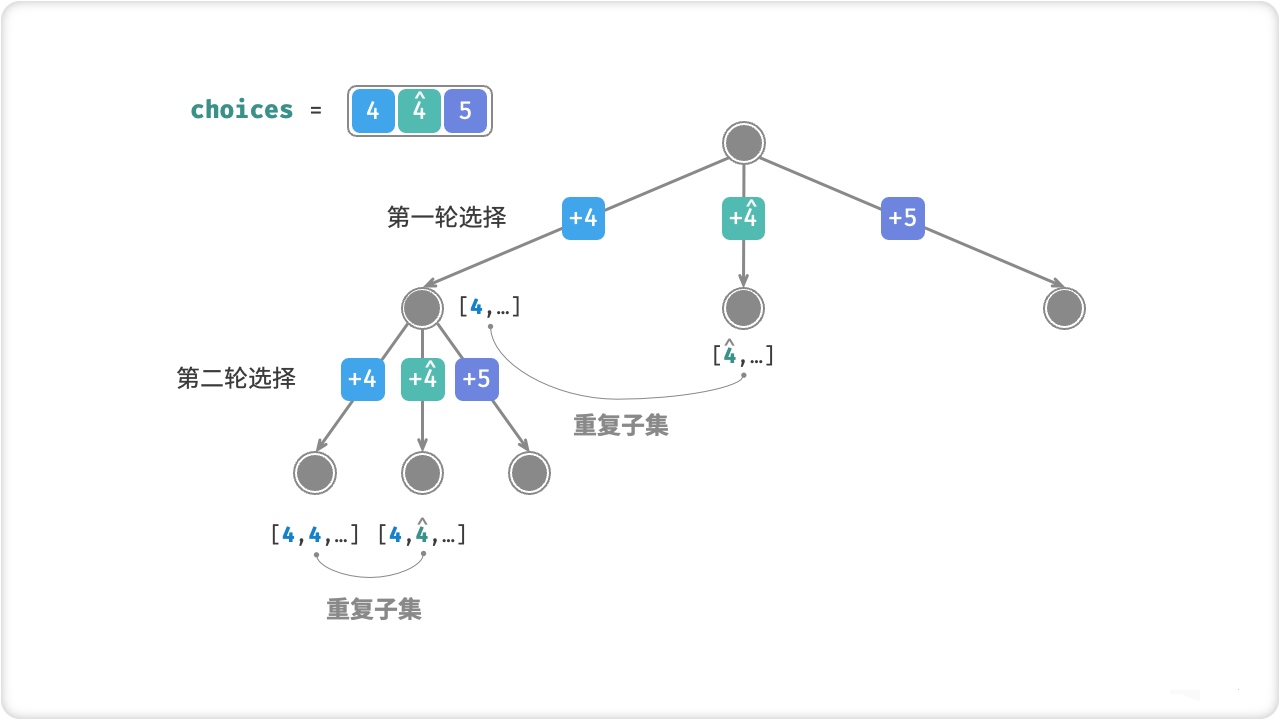
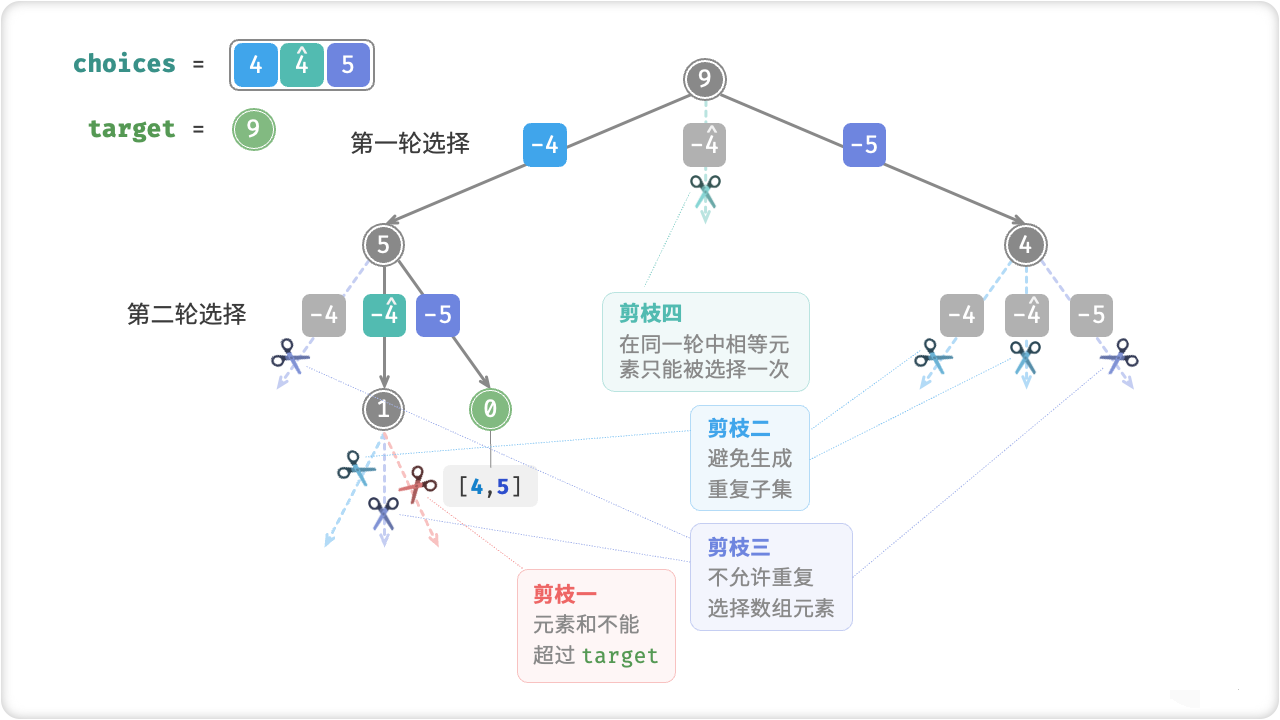
🦋3.2 有重复元素的情况
public class subset_sum_ii {
/* 回溯算法:子集和 II */
public static void backtrack(List<int> state, int target, int[] choices, int start, List<List<int>> res) {
// 子集和等于 target 时,记录解
if (target == 0) {
res.Add(new List<int>(state));
return;
}
// 遍历所有选择
// 剪枝二:从 start 开始遍历,避免生成重复子集
// 剪枝三:从 start 开始遍历,避免重复选择同一元素
for (int i = start; i < choices.Length; i++) {
// 剪枝一:若子集和超过 target ,则直接结束循环
// 这是因为数组已排序,后边元素更大,子集和一定超过 target
if (target - choices[i] < 0) {
break;
}
// 剪枝四:如果该元素与左边元素相等,说明该搜索分支重复,直接跳过
if (i > start && choices[i] == choices[i - 1]) {
continue;
}
// 尝试:做出选择,更新 target, start
state.Add(choices[i]);
// 进行下一轮选择
backtrack(state, target - choices[i], choices, i + 1, res);
// 回退:撤销选择,恢复到之前的状态
state.RemoveAt(state.Count - 1);
}
}
/* 求解子集和 II */
public static List<List<int>> subsetSumII(int[] nums, int target) {
List<int> state = new List<int>(); // 状态(子集)
Array.Sort(nums); // 对 nums 进行排序
int start = 0; // 遍历起始点
List<List<int>> res = new List<List<int>>(); // 结果列表(子集列表)
backtrack(state, target, nums, start, res);
return res;
}
[Test]
public void Test() {
int[] nums = { 4, 4, 5 };
int target = 9;
List<List<int>> res = subsetSumII(nums, target);
Console.WriteLine("输入数组 nums = " + string.Join(", ", nums) + ", target = " + target);
Console.WriteLine("所有和等于 " + target + " 的子集 res = ");
foreach (var subset in res) {
PrintUtil.PrintList(subset);
}
}
}
🔎4.N 皇后问题
N 皇后问题是指在 N*N 的棋盘上放置 N 个皇后,使得每个皇后都不会在同一行、同一列或同一斜线上。这是一个经典的回溯算法问题,其解法可以通过递归和剪枝实现。
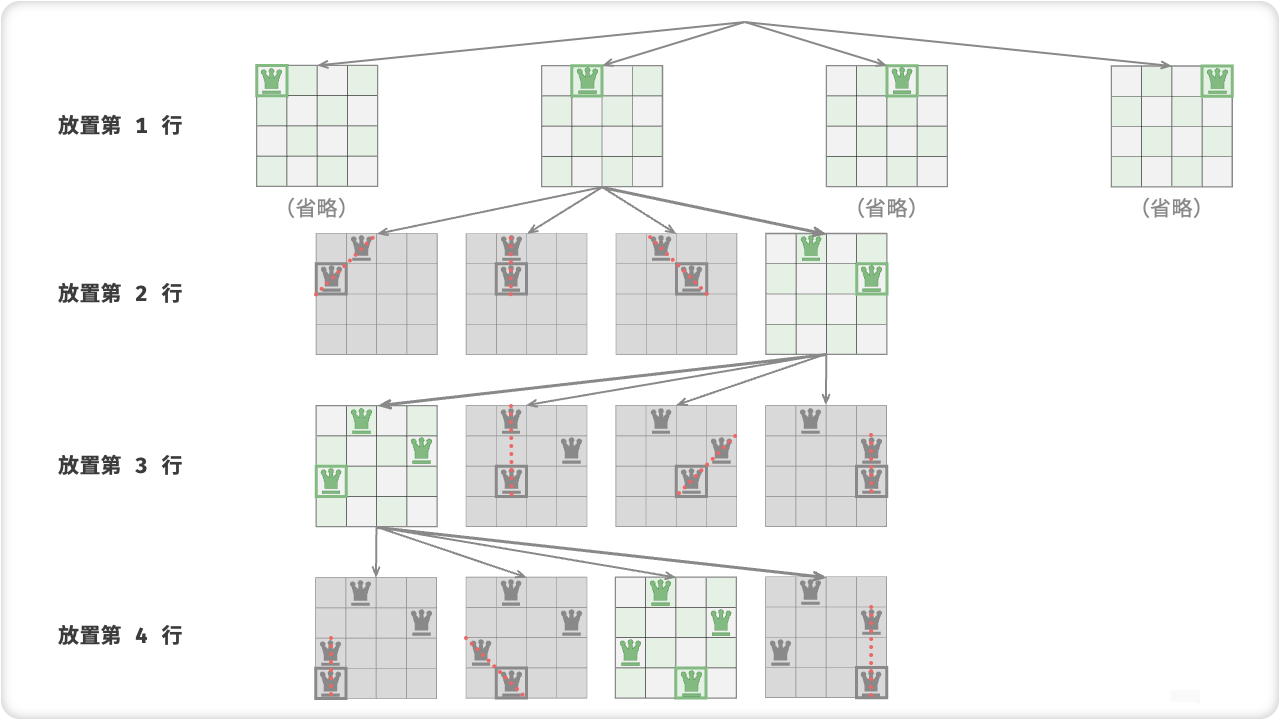
对于这个问题,我们可以采用一行一行地放置皇后的方法,从第一行开始逐行放置。在每一行中,我们尝试在该行的每一个位置都放置一个皇后,并检查当前放置是否合法。如果合法,我们继续递归地放置下一行的皇后。如果递归过程中发现某种情况不符合要求,则返回上一层进行回溯,尝试其他的位置。当递归到最后一行,且合法的放置方式已经找到时,我们就得到了一个合法解。
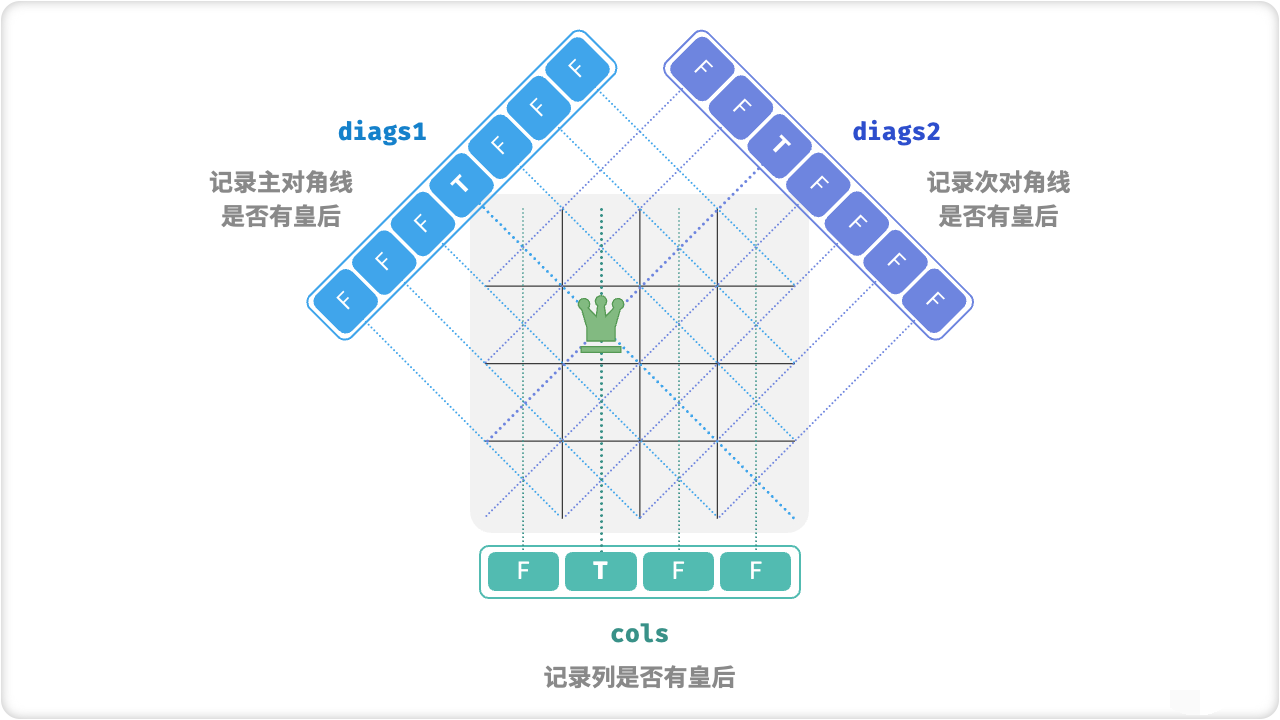
在实现过程中,我们需要注意如何检查放置是否合法。一种简单的方法是,对于每个位置检查其所在的行、列和两条对角线上是否已经有其他的皇后。如果没有,则该放置是合法的;否则,该放置是非法的。另一种更高效的方法是,使用三个集合来记录已经被占据的列、正对角线和斜对角线,从而避免重复判断。
N 皇后问题的时间复杂度为 O(N!),空间复杂度取决于具体实现方式。
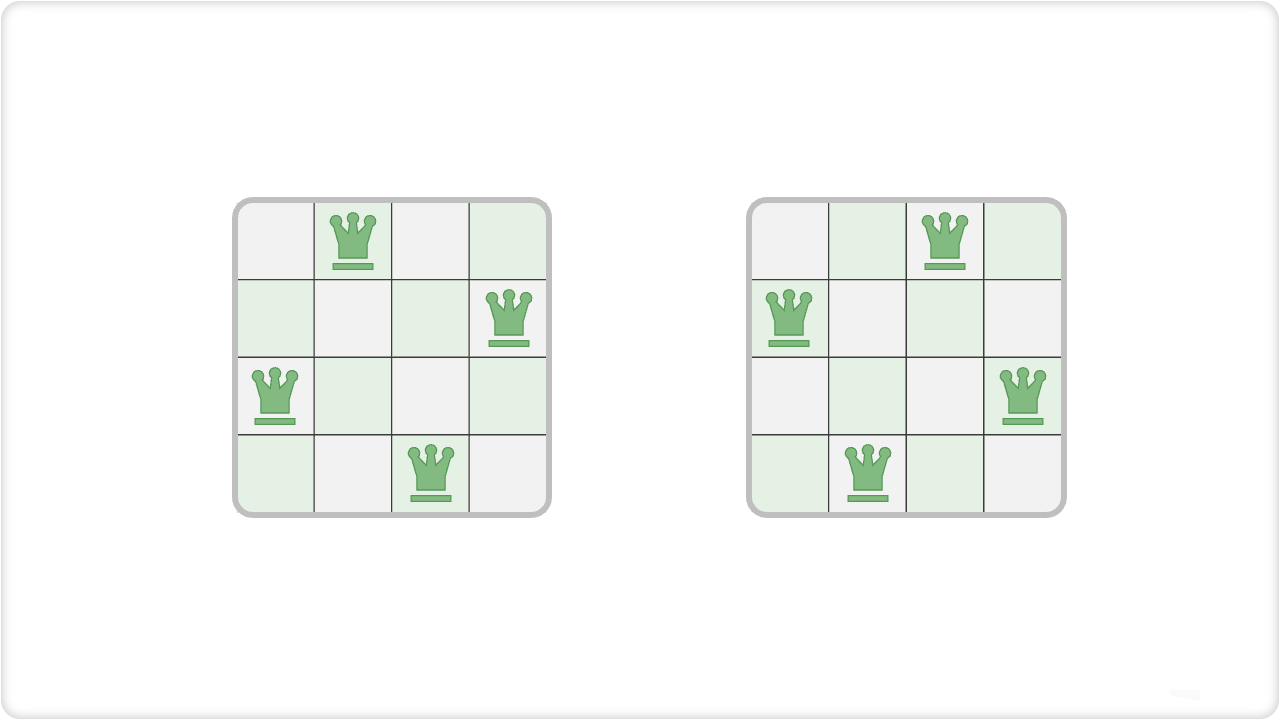
当 (n = 4) 时,共可以找到两个解。从回溯算法的角度看,(n \times n) 大小的棋盘共有 (n^2) 个格子,给出了所有的选择 choices 。在逐个放置皇后的过程中,棋盘状态在不断地变化,每个时刻的棋盘就是状态 state 。
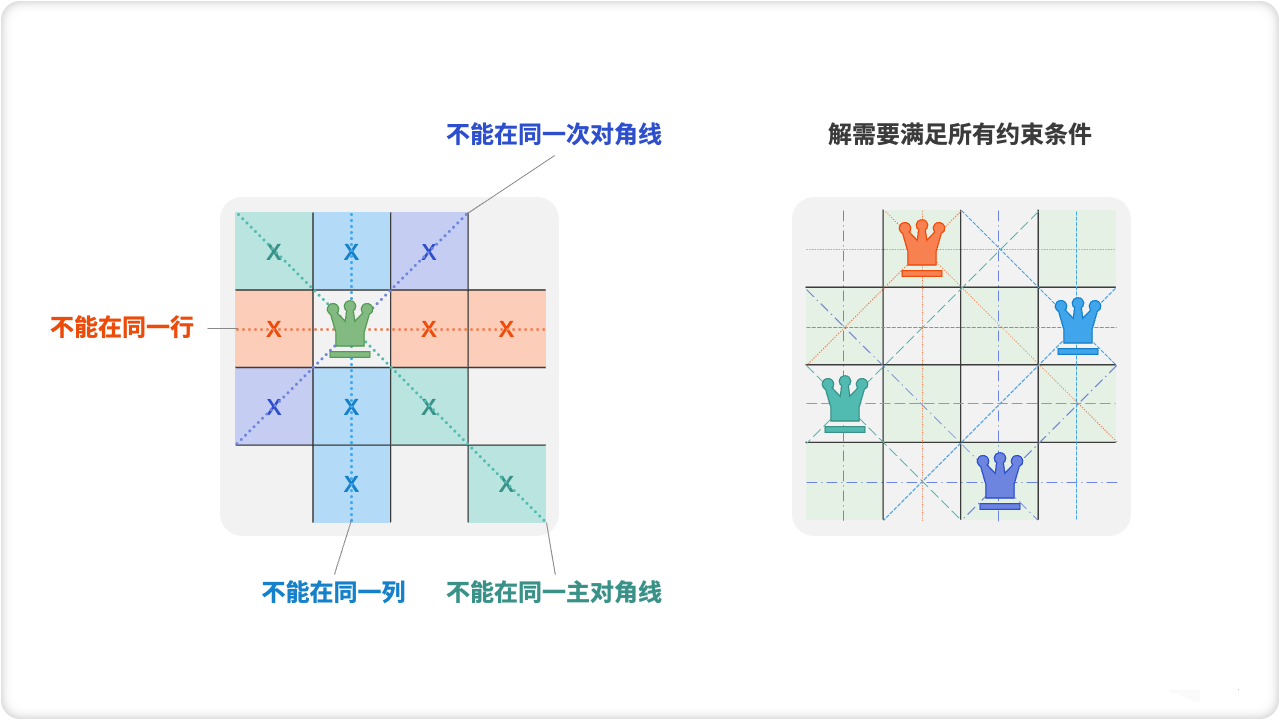
本题的三个约束条件:多个皇后不能在同一行、同一列、同一对角线。值得注意的是,对角线分为主对角线 \ 和次对角线 / 两种。
public class n_queens {
/* 回溯算法:N 皇后 */
static void backtrack(int row, int n, List<List<string>> state, List<List<List<string>>> res,
bool[] cols, bool[] diags1, bool[] diags2) {
// 当放置完所有行时,记录解
if (row == n) {
List<List<string>> copyState = new List<List<string>>();
foreach (List<string> sRow in state) {
copyState.Add(new List<string>(sRow));
}
res.Add(copyState);
return;
}
// 遍历所有列
for (int col = 0; col < n; col++) {
// 计算该格子对应的主对角线和副对角线
int diag1 = row - col + n - 1;
int diag2 = row + col;
// 剪枝:不允许该格子所在列、主对角线、副对角线存在皇后
if (!cols[col] && !diags1[diag1] && !diags2[diag2]) {
// 尝试:将皇后放置在该格子
state[row][col] = "Q";
cols[col] = diags1[diag1] = diags2[diag2] = true;
// 放置下一行
backtrack(row + 1, n, state, res, cols, diags1, diags2);
// 回退:将该格子恢复为空位
state[row][col] = "#";
cols[col] = diags1[diag1] = diags2[diag2] = false;
}
}
}
/* 求解 N 皇后 */
static List<List<List<string>>> nQueens(int n) {
// 初始化 n*n 大小的棋盘,其中 'Q' 代表皇后,'#' 代表空位
List<List<string>> state = new List<List<string>>();
for (int i = 0; i < n; i++) {
List<string> row = new List<string>();
for (int j = 0; j < n; j++) {
row.Add("#");
}
state.Add(row);
}
bool[] cols = new bool[n]; // 记录列是否有皇后
bool[] diags1 = new bool[2 * n - 1]; // 记录主对角线是否有皇后
bool[] diags2 = new bool[2 * n - 1]; // 记录副对角线是否有皇后
List<List<List<string>>> res = new List<List<List<string>>>();
backtrack(0, n, state, res, cols, diags1, diags2);
return res;
}
[Test]
public void Test() {
int n = 4;
List<List<List<string>>> res = nQueens(n);
Console.WriteLine("输入棋盘长宽为 " + n);
Console.WriteLine("皇后放置方案共有 " + res.Count + " 种");
foreach (List<List<string>> state in res) {
Console.WriteLine("--------------------");
foreach (List<string> row in state) {
PrintUtil.PrintList(row);
}
}
}
}
🚀感谢:给读者的一封信
亲爱的读者,
我在这篇文章中投入了大量的心血和时间,希望为您提供有价值的内容。这篇文章包含了深入的研究和个人经验,我相信这些信息对您非常有帮助。
如果您觉得这篇文章对您有所帮助,我诚恳地请求您考虑赞赏1元钱的支持。这个金额不会对您的财务状况造成负担,但它会对我继续创作高质量的内容产生积极的影响。
我之所以写这篇文章,是因为我热爱分享有用的知识和见解。您的支持将帮助我继续这个使命,也鼓励我花更多的时间和精力创作更多有价值的内容。
如果您愿意支持我的创作,请扫描下面二维码,您的支持将不胜感激。同时,如果您有任何反馈或建议,也欢迎与我分享。

再次感谢您的阅读和支持!
最诚挚的问候, “愚公搬代码”
- 点赞
- 收藏
- 关注作者


评论(0)