🏆 作者简介，愚公搬代码
🏆《头衔》：华为云特约编辑，华为云云享专家，华为开发者专家，华为产品云测专家，CSDN博客专家，阿里云专家博主，腾讯云优秀博主，掘金优秀博主，51CTO博客专家等。
🏆《近期荣誉》：2022年CSDN博客之星TOP2，2022年华为云十佳博主等。
🏆《博客内容》：.NET、Java、Python、Go、Node、前端、IOS、Android、鸿蒙、Linux、物联网、网络安全、大数据、人工智能、U3D游戏、小程序等相关领域知识。
🏆🎉欢迎 👍点赞✍评论⭐收藏

🚀前言

排序算法是一种将一组数据按照特定的规则进行排列的方法。排序算法通常用于对数据的处理，使得数据能够更容易地被查找、比较和分析。

下面是常见的11种排序算法：

1. 冒泡排序（Bubble Sort）：比较相邻的元素，如果前面的元素大于后面的元素，就交换这两个元素的位置。时间复杂度为O(n^2)。

2. 选择排序（Selection Sort）：在未排序的数据中找到最小（大）的元素，放置在已排序的数据末尾。时间复杂度为O(n^2)。

3. 插入排序（Insertion Sort）：将未排序的元素插入到已排序的序列中，时间复杂度为O(n^2)。

4. 希尔排序（Shell Sort）：希尔排序是插入排序的一种改进，它将原序列分割成若干个子序列，对每个子序列进行插入排序，最后对整个序列进行插入排序。时间复杂度为O(nlogn)。

5. 二路归并排序（Merge Sort）：二路归并排序是指将一个序列分成两个子序列，分别对两个子序列进行归并排序，然后将排序好的两个子序列合并成一个有序序列的过程。这种排序思想采用了分治算法的思想，排序效率较高，时间复杂度为 O(nlogn)。

6. 快速排序（Quick Sort）：选择一个基准元素，将大于基准元素的数放在一边，小于基准元素的数放在另一边，递归执行该过程，最后得到有序序列。时间复杂度为O(nlogn)。

7. 堆排序（Heap Sort）：将序列转换为一个大根堆，每次将堆顶元素与堆底元素交换，然后将剩余元素重新构建堆，重复执行该过程，最后得到有序序列。时间复杂度为O(nlogn)。

8. 计数排序（Counting Sort）：统计小于等于每个元素的个数，再依次计算出每个元素在有序序列中的位置。时间复杂度为O(n+k)，其中k为最大元素值。

9. 桶排序（Bucket Sort）：将元素分到多个桶中，对每个桶进行排序，最后将所有桶中的元素按顺序合并起来。时间复杂度为O(n)。

10. 基数排序（Radix Sort）：按照低位到高位的顺序对元素进行排序，依次排序后得到有序序列。时间复杂度为O(dn)，其中d为元素的位数。

11. 多路归并排序：多路归并排序是指将一个序列分成多个子序列，然后对每个子序列进行排序，最后将排好序的子序列合并成一个有序序列的过程。多路归并排序的时间复杂度不仅取决于序列长度，还取决于子序列个数。多路归并排序的优点是可以对比二路归并排序更加高效地利用计算机的多核心处理能力，因此在大规模数据处理中有广泛的应用。

🚀一、选择排序

🔎1.基本思想

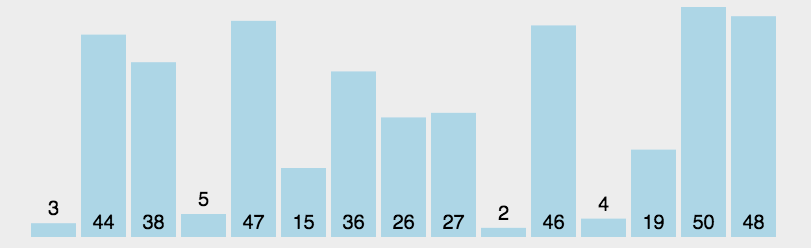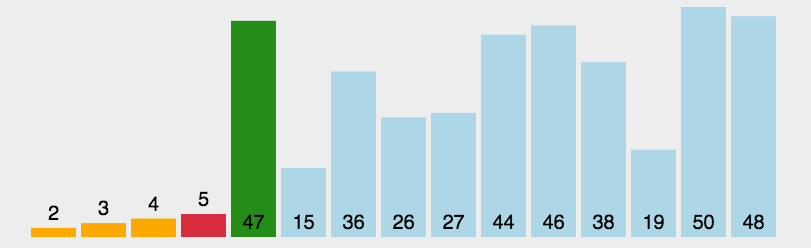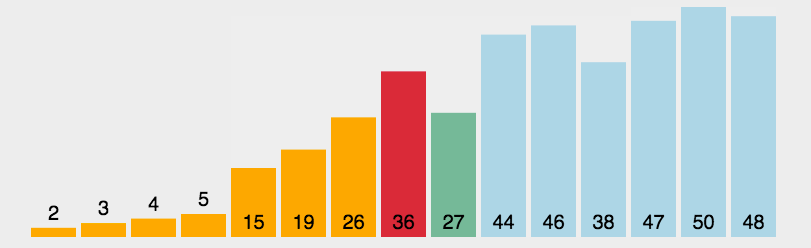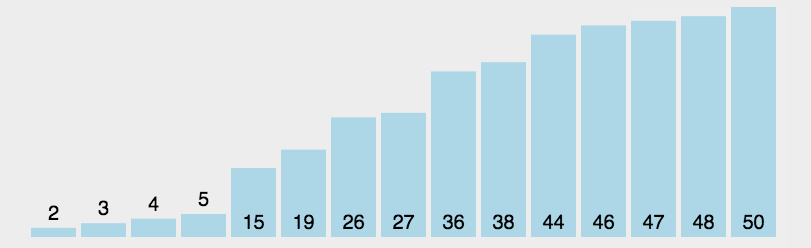
选择排序的基本思想是：在未排序的序列中，找到最小的元素，将其放置在序列的起始位置；然后从剩余未排序的元素中，继续找到最小的元素，放置在已排序序列的末尾；以此类推，直到所有元素都排完为止。这个过程可以看作是不断选择剩余元素中的最小值，将其放置在已排序序列的末尾的过程。这个过程类似于打牌时从一堆牌中选择最小的牌放到手中的牌堆里，然后再从剩余的牌中选择最小的牌放到手中的牌堆的末尾，直到所有牌都被选完为止。

🔎2.复杂度分析

选择排序的时间复杂度为$O(n^2)$，空间复杂度为$O(1)$。具体分析如下：

在选择排序过程中，需要找出剩余元素中的最小值，并将其放到已排序部分的末尾。假设待排序的数组长度为n，则第一次找最小值需要比较n-1次，第二次找最小值需要比较n-2次，以此类推，总的比较次数为：

$$(n-1)+(n-2)+\cdots+2+1=\frac{n(n-1)}{2}$$

因此，比较的时间复杂度为$O(n^2)$。

在选择排序过程中，只需要在原数组中进行元素的交换操作，不需要创建新的数组或者其他数据结构来保存中间结果，因此空间复杂度为$O(1)$。

选择排序的时间复杂度为$O(n^2)$，空间复杂度为$O(1)$。

🔎3.应用场景

选择排序适用于数据量较小、内存消耗较少的情况，不建议用于大规模数据排序。以下是选择排序的几个应用场景：

1. 数据量较小的排序场景：由于选择排序的时间复杂度为O(n^2)，因此适用于数据量较小的排序场景，比如10万以下的数据量。

2. 内存消耗有限的场景：选择排序不需要额外的内存空间，只需要一个临时变量来交换元素，因此适用于内存消耗有限的场景。

3. 初学者学习算法的练习场景：选择排序是比较简单、容易理解的排序算法，适合初学者学习算法时进行练习。

4. 数据基本有序的场景：选择排序在处理数据基本有序的情况下，效率比冒泡排序要高，因为选择排序只需要进行n-1次比较，而冒泡排序需要进行n^2次比较。

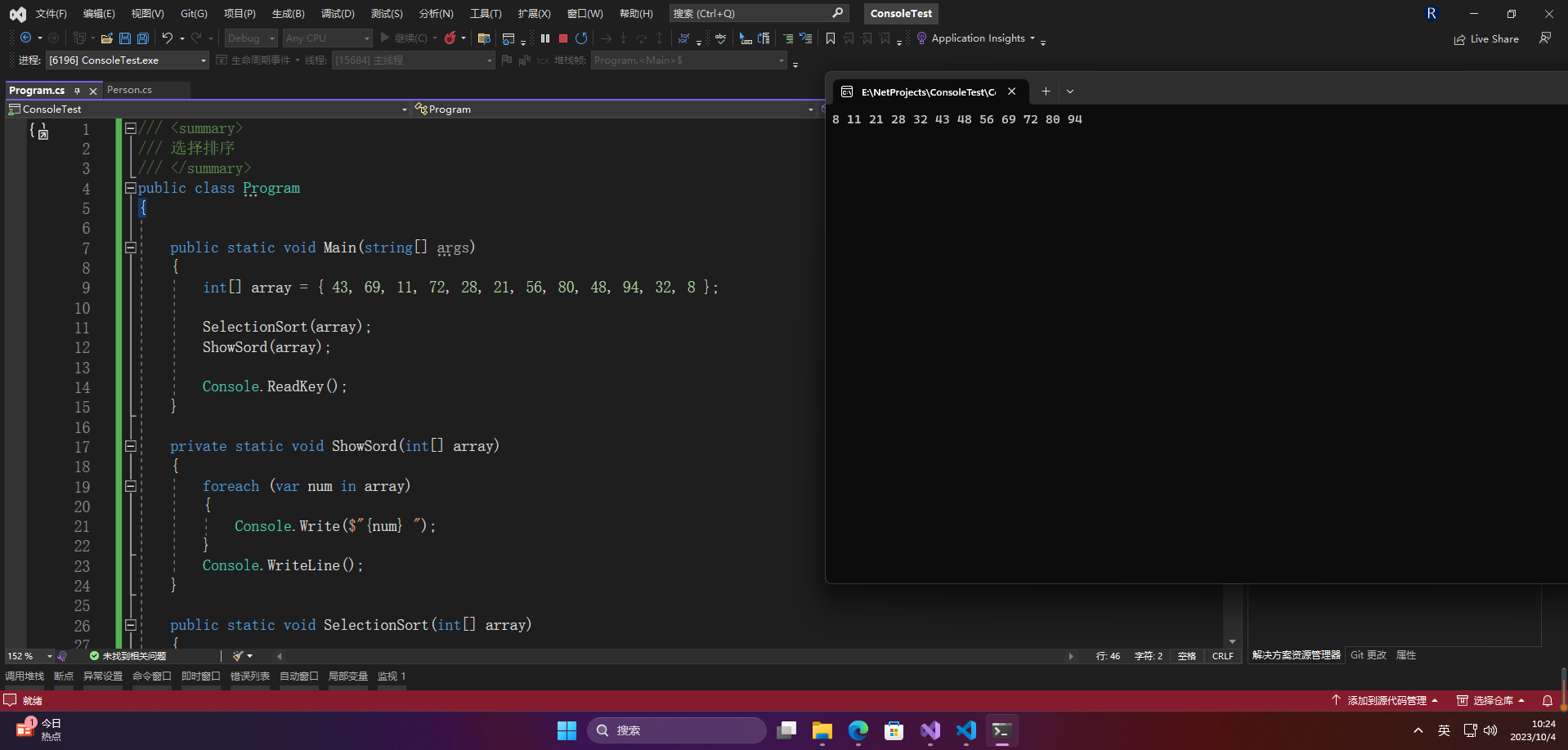
🔎4.示例

/// <summary>
/// 选择排序
/// </summary>
public class Program {

    public static void Main(string[] args) {
        int[] array = { 43, 69, 11, 72, 28, 21, 56, 80, 48, 94, 32, 8 };

        SelectionSort(array);
        ShowSord(array);

        Console.ReadKey();
    }

    private static void ShowSord(int[] array) {
        foreach(var num in array) {
            Console.Write($"{num} ");
        }
        Console.WriteLine();
    }

    public static void SelectionSort(int[] array) {
        int swap;
        int pos = 0;
        for(int i = 0; i < array.Length - 1; i++) {
            pos = i;
            for(int j = i + 1; j < array.Length; j++) {
                if(array[j] < array[pos]) {
                    pos = j;
                }
            }
            swap = array[pos];
            array[pos] = array[i];
            array[i] = swap;
        }
    }

}

🚀感谢：给读者的一封信

亲爱的读者，

我在这篇文章中投入了大量的心血和时间，希望为您提供有价值的内容。这篇文章包含了深入的研究和个人经验，我相信这些信息对您非常有帮助。

如果您觉得这篇文章对您有所帮助，我诚恳地请求您考虑赞赏1元钱的支持。这个金额不会对您的财务状况造成负担，但它会对我继续创作高质量的内容产生积极的影响。

我之所以写这篇文章，是因为我热爱分享有用的知识和见解。您的支持将帮助我继续这个使命，也鼓励我花更多的时间和精力创作更多有价值的内容。

如果您愿意支持我的创作，请扫描下面二维码，您的支持将不胜感激。同时，如果您有任何反馈或建议，也欢迎与我分享。

再次感谢您的阅读和支持！

最诚挚的问候， “愚公搬代码”