【愚公系列】2023年12月 七大查找算法(三)-插值查找
🏆 作者简介,愚公搬代码
🏆《头衔》:华为云特约编辑,华为云云享专家,华为开发者专家,华为产品云测专家,CSDN博客专家,阿里云专家博主,腾讯云优秀博主,掘金优秀博主,51CTO博客专家等。
🏆《近期荣誉》:2022年CSDN博客之星TOP2,2022年华为云十佳博主等。
🏆《博客内容》:.NET、Java、Python、Go、Node、前端、IOS、Android、鸿蒙、Linux、物联网、网络安全、大数据、人工智能、U3D游戏、小程序等相关领域知识。
🏆🎉欢迎 👍点赞✍评论⭐收藏
🚀前言
在编程语言中,查找算法是指在一个数据集合中查找某个元素是否存在的算法。常见的查找算法包括:
-
顺序查找(Sequential Search):逐个遍历数据集来查找目标元素,时间复杂度为O(n)。
-
二分查找(Binary Search):在有序数据集合中,从中间位置作为起点不断划分区间并查找,时间复杂度为O(log n)。
-
插值查找(Interpolation Search):在有序数据集合中,根据目标元素与数据集合首尾之间的差值,利用插值估算目标元素的位置,时间复杂度为O(log log n)或O(n)。
-
斐波那契查找(Fibonacci Search):在有序数据集合中,根据斐波那契数列调整中间点的位置来查找,时间复杂度为O(log n)。
-
B树查找(B-Tree Search):在平衡的B树中查找元素,时间复杂度为O(log n)。
-
哈希查找(Hash Search):通过哈希函数将元素映射到哈希表中,并在哈希表中查找元素,时间复杂度为O(1)。
-
分块查找(Block Search):将数据集合划分为若干块,在每个块中进行二分查找或顺序查找,时间复杂度为O(sqrt(n))。
以上算法都有各自适用的场景,开发者需要根据数据集合的特性和需求选择最适合的算法来进行查找。
🚀一、插值查找
🔎1.基本思想
插值查找算法基于二分查找算法,但是它对于数据分布较为均匀的情况下,能够提供更快的查找效率。
其基本思想是根据要查找的关键字值计算出一个相对位置,然后根据这个位置来进行查找。具体实现步骤如下:
-
根据要查找的关键字值和数组的第一个元素和最后一个元素的值,计算出要查找的元素在数组中的位置估计值。公式为:$$ pos = low + \frac{(key - arr[low]) \times (high - low)}{arr[high]-arr[low]} $$ 其中,arr为有序数组,key为要查找的关键字,low为数组的第一个元素的下标,high为数组的最后一个元素的下标。
-
如果估计值等于要查找的元素,则查找成功并返回下标。否则,将估计值与要查找的元素进行比较。
-
如果估计值小于要查找的元素,则在数组右半部分继续进行查找。否则,在数组左半部分继续进行查找。
-
重复步骤1~3,直到查找成功或者查找失败为止。
插值查找算法的时间复杂度为O(logn),但是它只适用于有序的连续元素结构,例如数组或有序表。如果数据分布不均匀,则会降低查找效率。
🔎2.复杂度分析
插值查找算法是一种二分查找算法的优化,将查找点的选取与查找值的分布情况联系起来,可以更快地找到目标值。其时间复杂度取决于查找值的分布情况,最好情况下为 O(loglogn),最坏情况下为 O(n),平均情况下为 O(loglogn)。
具体分析如下:
-
最好情况下,当查找值刚好在数组的中间位置时,查找的过程就可以直接结束,此时时间复杂度为 O(1)。
-
最坏情况下,当查找值在数组的两端时,每次查找都跨越了一大段,此时时间复杂度为 O(n)。
-
平均情况下,假设数组中查找值均匀分布,则每次查找时,可以大致估计目标值所在的位置,从而跨越更少的距离进行查找,时间复杂度可以达到 O(loglogn)。
总的来说,插值查找算法时间复杂度的效果取决于查找值在数组中的分布情况,如果分布均匀,则效果比较好,否则可能会退化为线性查找,效率较低。
🔎3.应用场景
插值查找算法适用于以下情况:
-
数据分布均匀的有序数组,且数据量较大。
-
数组中的数据有序排列,但是数据之间的差值不是固定的。比如:学生成绩(90、92、95、96、98、98、99、100)。
-
由于每次查找前都会根据查找值的大小动态计算查找的位置,因此适用于数据频繁变动的场景,比如动态更新的数据库。
插值查找算法适用于数据分布比较均匀,查找频率较高的有序数组场景,这种场景下插值查找算法可能会比二分查找效率更高。
🔎4.示例
int[] array = { 8, 11, 21, 28, 32, 43, 48, 56, 69, 72, 80, 94 };
Console.WriteLine(InterpolationSearch(array, 80, 0, array.Length - 1));
Console.ReadKey();
static int InterpolationSearch(int[] array, int key, int low, int high)
{
if (low > high) return -1;
var mid = (int)(low + ((double)key - array[low]) /
(array[high] - array[low]) * (high - low));
if (array[mid] == key)
return mid;
else if (array[mid] > key)
return InterpolationSearch(array, key, low, mid - 1);
else
return InterpolationSearch(array, key, mid + 1, high);
}
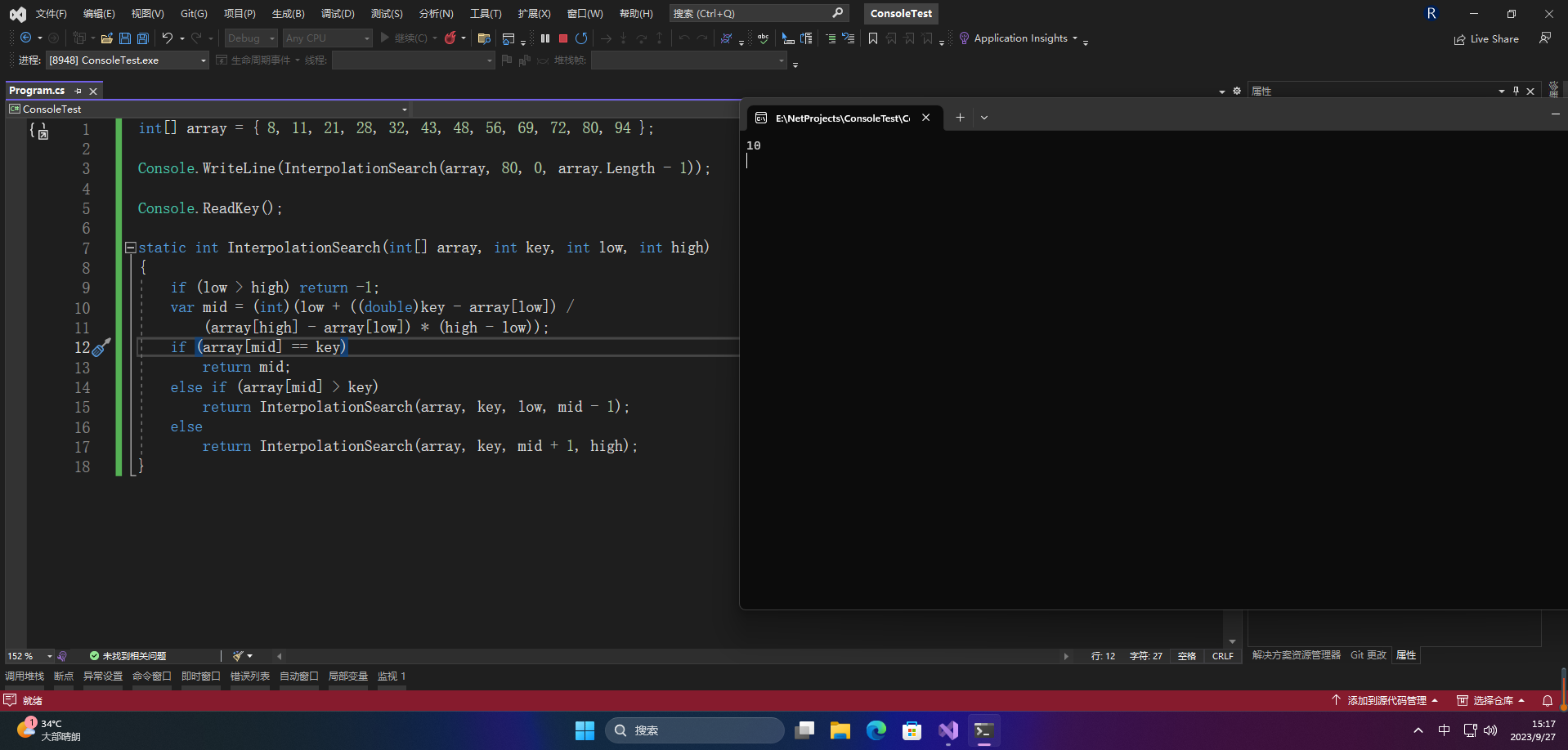
在最坏的情况下插值查找的时间复杂度为: O(log(logn)) 。
🚀感谢:给读者的一封信
亲爱的读者,
我在这篇文章中投入了大量的心血和时间,希望为您提供有价值的内容。这篇文章包含了深入的研究和个人经验,我相信这些信息对您非常有帮助。
如果您觉得这篇文章对您有所帮助,我诚恳地请求您考虑赞赏1元钱的支持。这个金额不会对您的财务状况造成负担,但它会对我继续创作高质量的内容产生积极的影响。
我之所以写这篇文章,是因为我热爱分享有用的知识和见解。您的支持将帮助我继续这个使命,也鼓励我花更多的时间和精力创作更多有价值的内容。
如果您愿意支持我的创作,请扫描下面二维码,您的支持将不胜感激。同时,如果您有任何反馈或建议,也欢迎与我分享。

再次感谢您的阅读和支持!
最诚挚的问候, “愚公搬代码”
- 点赞
- 收藏
- 关注作者


评论(0)