【愚公系列】2023年12月 数据结构(十四)-图
🏆 作者简介,愚公搬代码
🏆《头衔》:华为云特约编辑,华为云云享专家,华为开发者专家,华为产品云测专家,CSDN博客专家,阿里云专家博主,腾讯云优秀博主,掘金优秀博主,51CTO博客专家等。
🏆《近期荣誉》:2022年CSDN博客之星TOP2,2022年华为云十佳博主等。
🏆《博客内容》:.NET、Java、Python、Go、Node、前端、IOS、Android、鸿蒙、Linux、物联网、网络安全、大数据、人工智能、U3D游戏、小程序等相关领域知识。
🏆🎉欢迎 👍点赞✍评论⭐收藏
🚀前言
数据结构是计算机科学中的一个重要概念,它描述了数据之间的组织方式和关系,以及对这些数据的访问和操作。常见的数据结构有:数组、链表、栈、队列、哈希表、树、堆和图。
-
数组(Array):是一种线性数据结构,它将一组具有相同类型的数据元素存储在一起,并为每个元素分配一个唯一的索引。数组的特点是具有随机访问的能力。
-
链表(Linked List):也是一种线性数据结构,它由一系列的节点组成,每个节点包含数据和指向下一个节点的引用。链表的特点是可以动态地插入或删除节点,但访问某个节点时需要从头开始遍历。
-
栈(Stack):是一种后进先出(LIFO)的数据结构,它只能在栈顶进行插入和删除操作。栈通常用于实现递归算法、表达式求值和内存管理等场景。
-
队列(Queue):是一种先进先出(FIFO)的数据结构,它可以在队尾插入元素,在队头删除元素。队列通常用于数据的缓存、消息队列和网络通信等场景。
-
哈希表(Hash Table):也称为散列表,它是一种根据关键字直接访问数据的数据结构。哈希表通常由数组和散列函数组成,可以在常数时间内进行插入、删除和查找操作。
-
树(Tree):是一种非线性数据结构,它由一系列的节点组成,每个节点可以有若干个子节点。树的特点是可以动态地插入或删除节点,常见的树结构包括二叉树、平衡树和搜索树等。
-
堆(Heap):是一种特殊的树结构,它通常用于实现优先队列和堆排序等算法。堆分为最大堆和最小堆,最大堆的每个节点的值都大于等于其子节点的值,最小堆则相反。
-
图(Graph):是一种由节点和边组成的非线性数据结构,它可以用来表示各种实体之间的关系,如社交网络、路线图和电路图等。图的遍历和最短路径算法是常见的图算法。
🚀一、图
🔎1.基本思想
图是一种非线性数据结构,它由节点(顶点)和连接这些节点的边(边)组成。图用于描述不同对象之间的关系,例如人与人之间的社交网络、城市与道路之间的地理网络等。
图的基本思想包括以下几个方面:
-
节点和边的表示:图中的节点通常用一个唯一标识符表示,边则用一组连接两个节点的有向或无向边表示。
-
图的存储方式:图的存储方式通常有两种,即邻接矩阵和邻接表。邻接矩阵用二维数组表示,记录任意两个节点之间是否有边;邻接表则使用链表来表示每个节点的邻接节点。
-
图的遍历:图的遍历是指按照一定规则访问图中的所有节点。常用的遍历算法有深度优先搜索(DFS)和广度优先搜索(BFS)。DFS从某个节点开始遍历图,先访问它的所有邻接节点,再依次访问它们的邻接节点。BFS则从某个节点开始,先访问它的所有邻接节点,再按照距离从小到大依次访问它们的邻接节点。
-
最短路径:在图中,最短路径是指从一个节点到另一个节点的最短距离。常用的算法有Dijkstra算法和Floyd算法。Dijkstra算法通过贪心策略选取当前距离起点最小的节点,并更新其它节点的距离,直到到达终点。Floyd算法则通过动态规划求解所有节点之间的最短路径。
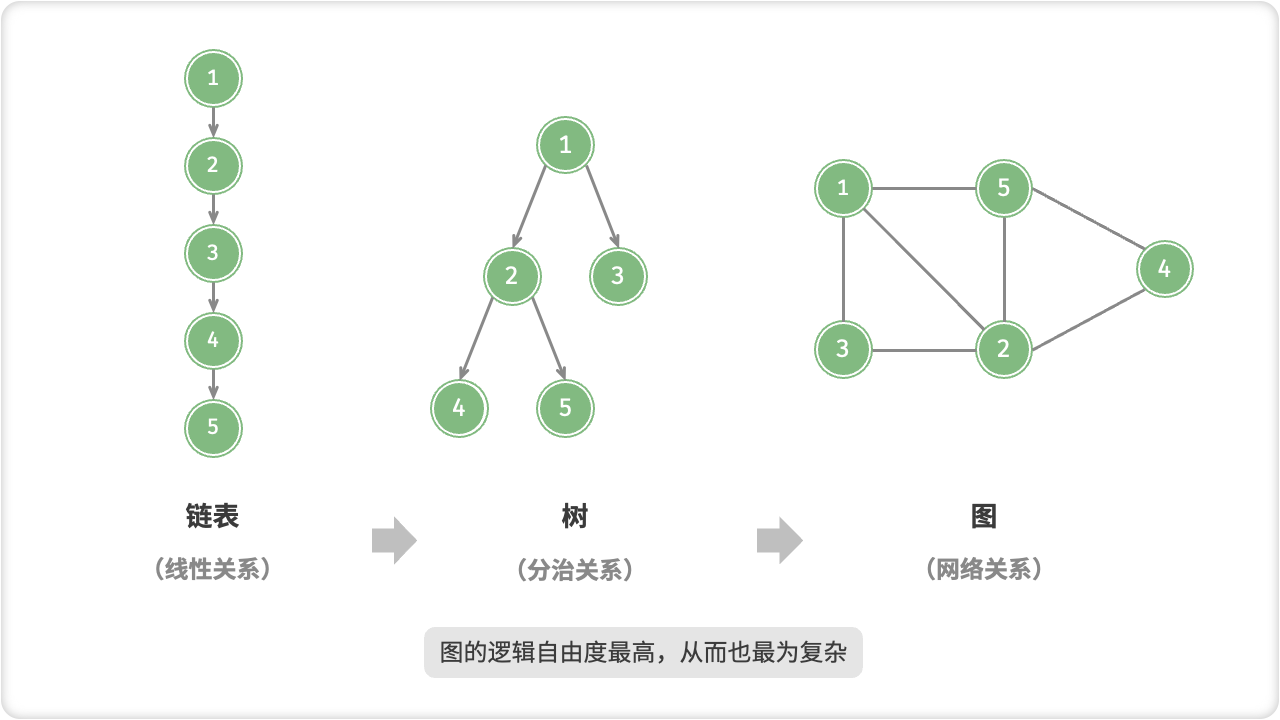
🦋1.1 图常见类型与术语
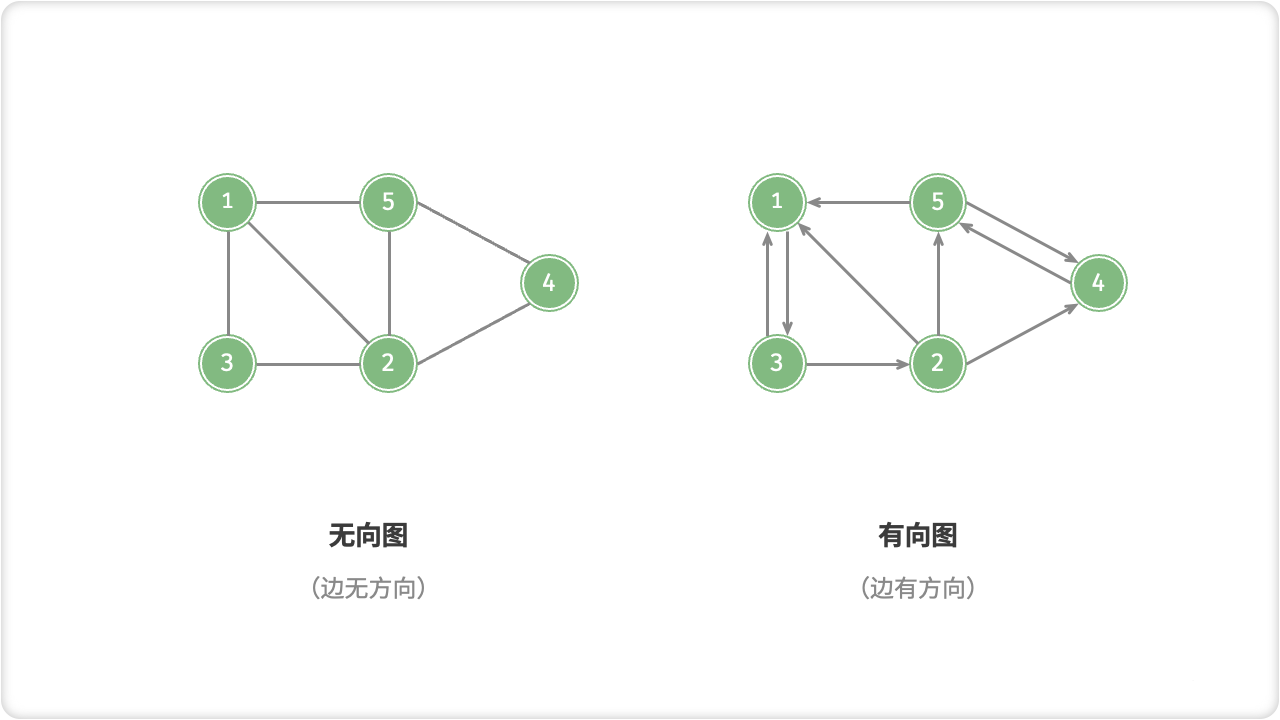
☀️1.1.1 无向图和有向图
无向图和有向图是两种常见的图形结构,都是由节点和边构成的。
无向图:每个节点之间的边没有方向,可以双向通行。例如,A节点和B节点之间存在一条边,即A->B和B->A都可以。
有向图:每个节点之间的边有方向,只能单向通行。例如,A节点指向B节点,即A->B,但B节点不能指向A节点。
在算法和数据结构中,无向图和有向图有不同的应用场景和算法。例如,最短路径算法只适用于无向图,而拓扑排序则只适用于有向图。
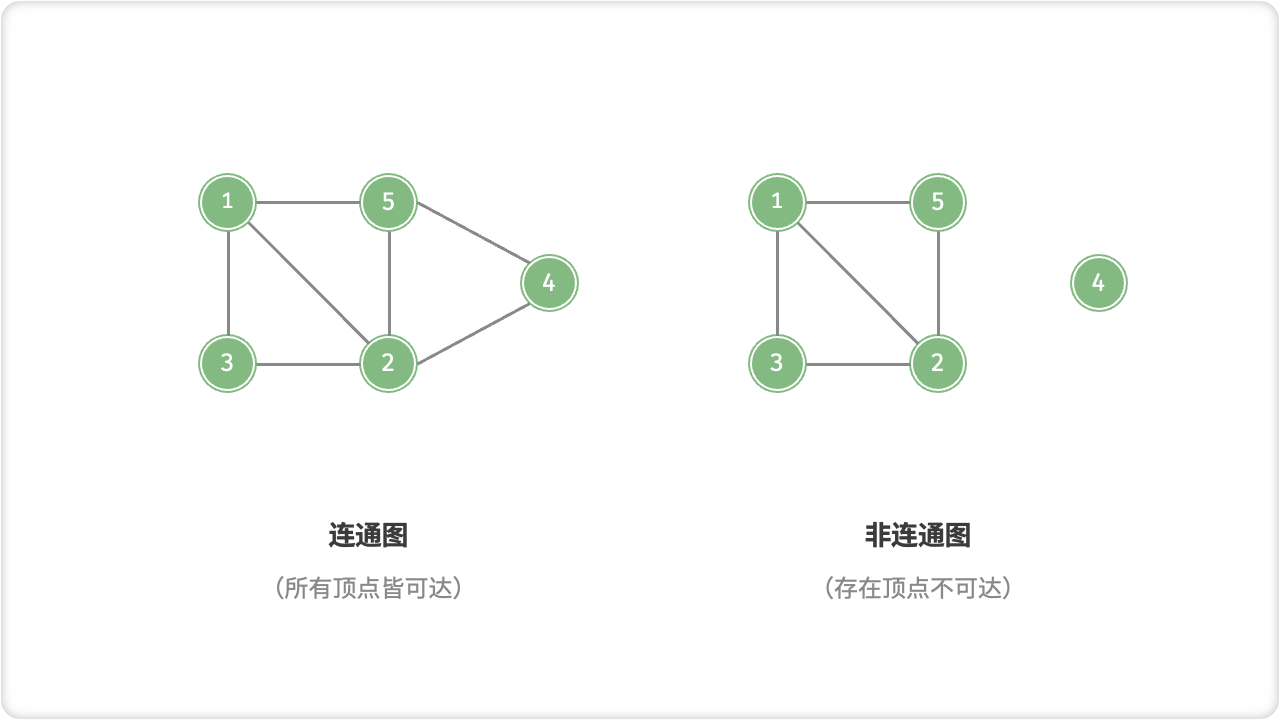
☀️1.1.2 连通图和非连通图
连通图是指图中任意两个顶点都可以通过路径相互到达的图,即不存在孤立的顶点。非连通图是指由多个连通分量组成的图,其中连通分量指的是一个连通的无向图。
在数据结构中,图的连通性具有重要意义。常用的检测图的连通性的算法有深度优先搜索和广度优先搜索。对于连通图,任意一个顶点可以作为起点进行遍历,而对于非连通图,则需要从未被遍历的顶点开始,继续遍历其他连通分量。
在实际应用中,连通图可以用来表示网络结构、社交网络等,非连通图可以用来表示多个独立的关系网。在算法设计中,连通图和非连通图的性质和特点也都需要被考虑到,以便设计出更加高效的算法。
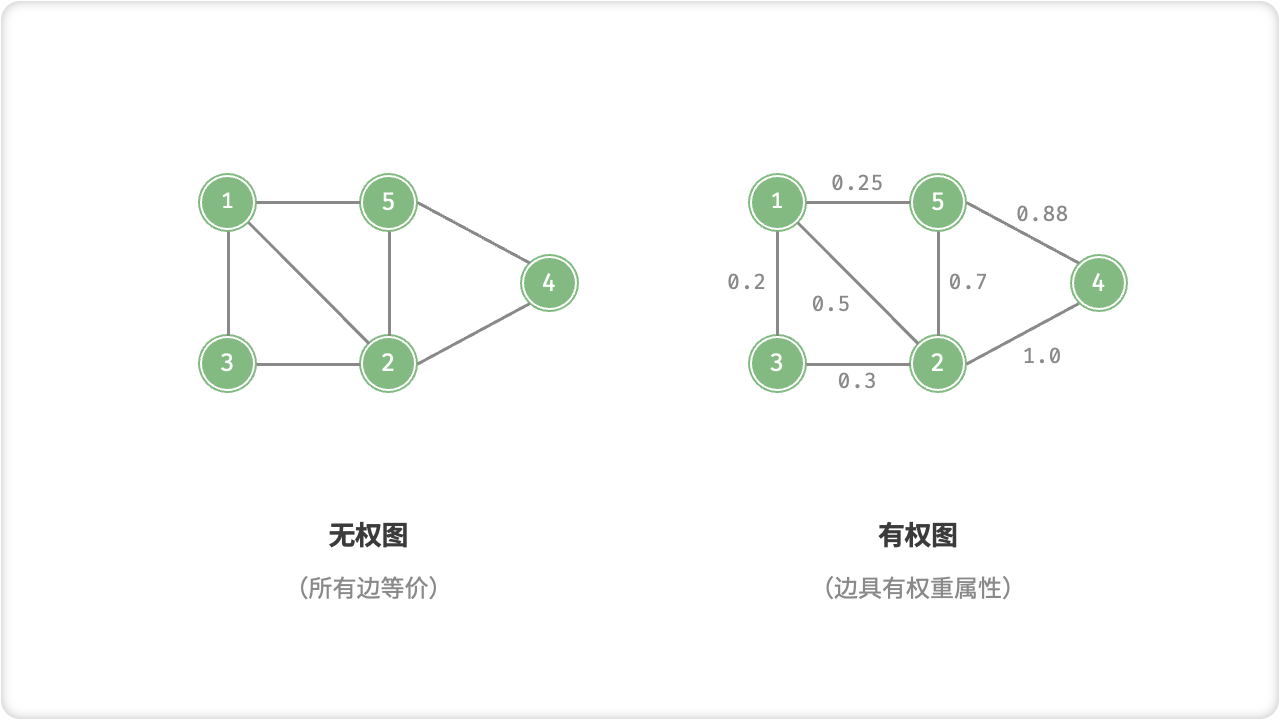
☀️1.1.3 无权图和有权图
无权图指的是图中每条边都没有权值或权重,只有节点之间的连接关系。在无权图中,寻找最短路径的算法可以使用广度优先搜索(BFS)。
有权图则是指图中每条边都有权值或权重,表示这条边的代价或距离。在有权图中,寻找最短路径的算法可以使用Dijkstra算法或A*算法。此外,有权图还可以用于最小生成树的问题,最常用的算法是Prim算法和Kruskal算法。
🦋1.2 图的表示
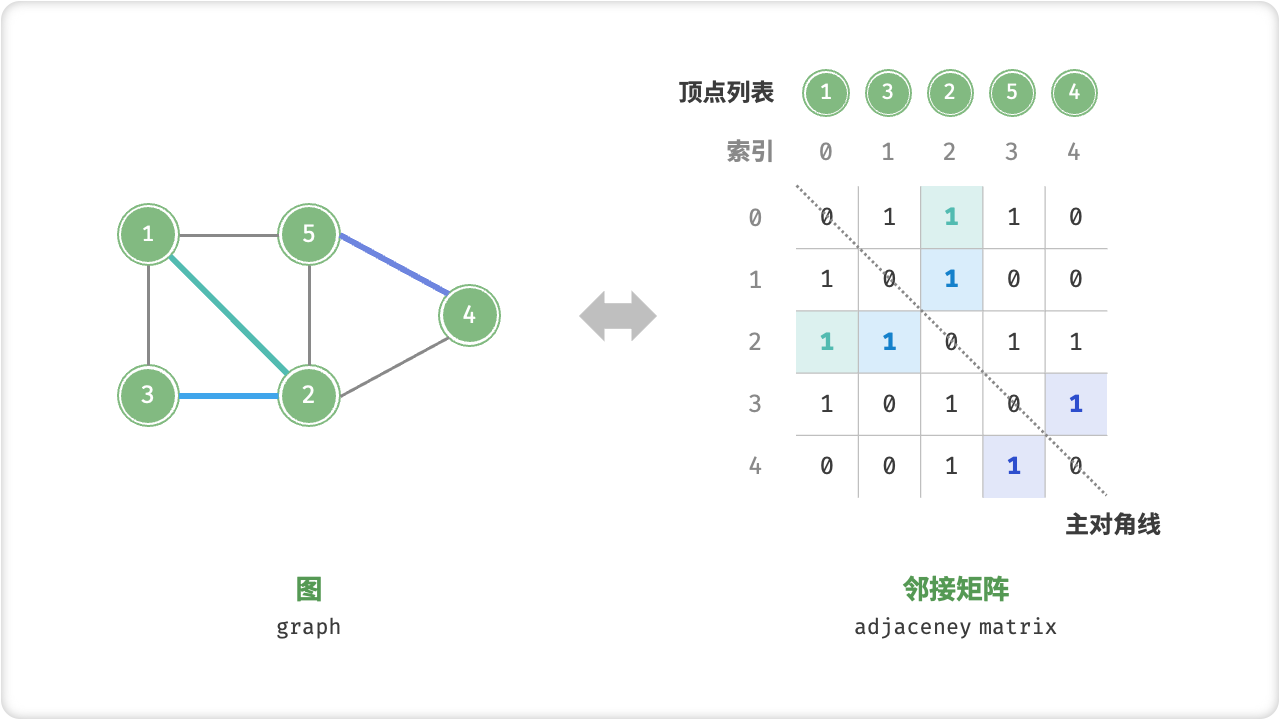
☀️1.2.1 邻接矩阵
邻接矩阵是一种用于表示图的数据结构,它是一个二维数组,其中数组的每个元素表示两个顶点之间是否有边。具体地,数组中每个元素的值为1表示存在边;为0表示不存在边。当图是有向图时,邻接矩阵是一个方阵,且只需要考虑一条边的方向。
邻接矩阵的优点是可以快速地判断两个顶点之间是否有边,时间复杂度为O(1),同时还可以在常数时间内获取一个顶点的所有相邻顶点。另外,邻接矩阵也比较容易实现存储和操作。
但是邻接矩阵的缺点是它需要占用大量的空间,尤其是当图比较稀疏时,即边数比顶点数的平方要小很多时,存储大量的0是浪费空间的。此外,邻接矩阵只适合表示静态图,即图中的边不会频繁地增加或删除。如果需要频繁地修改边,则需要重新分配内存,操作比较耗时。
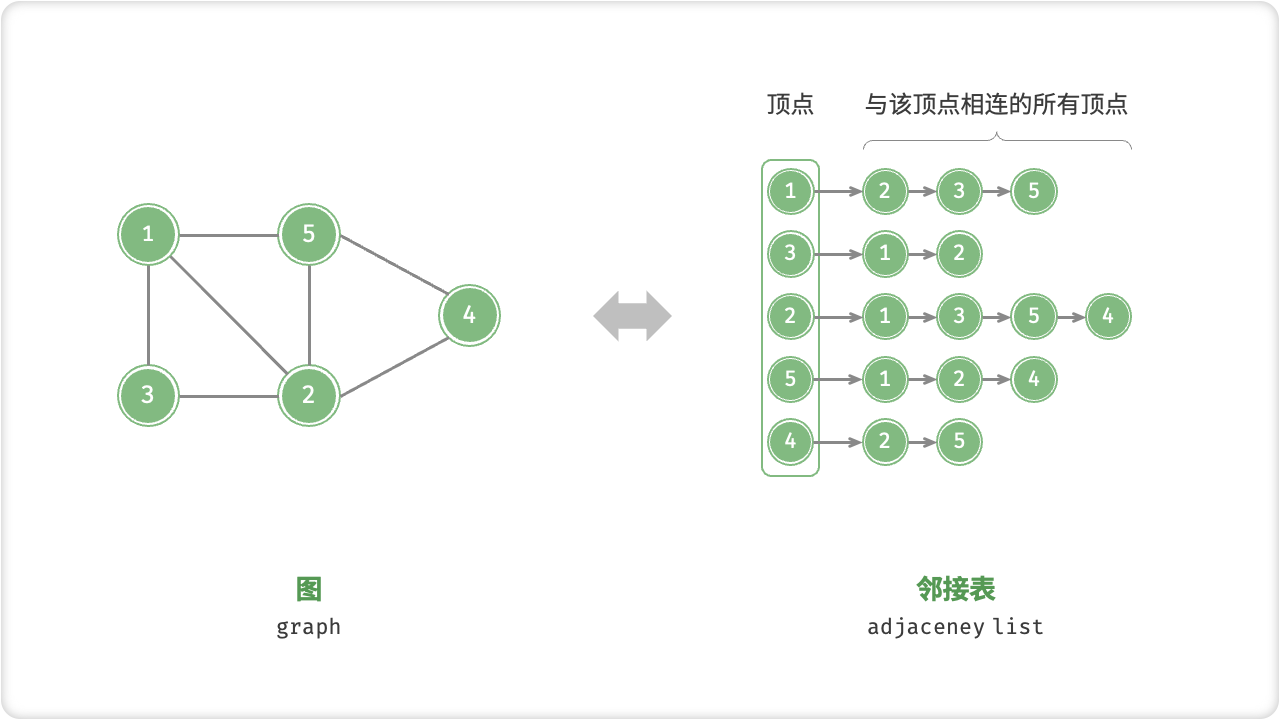
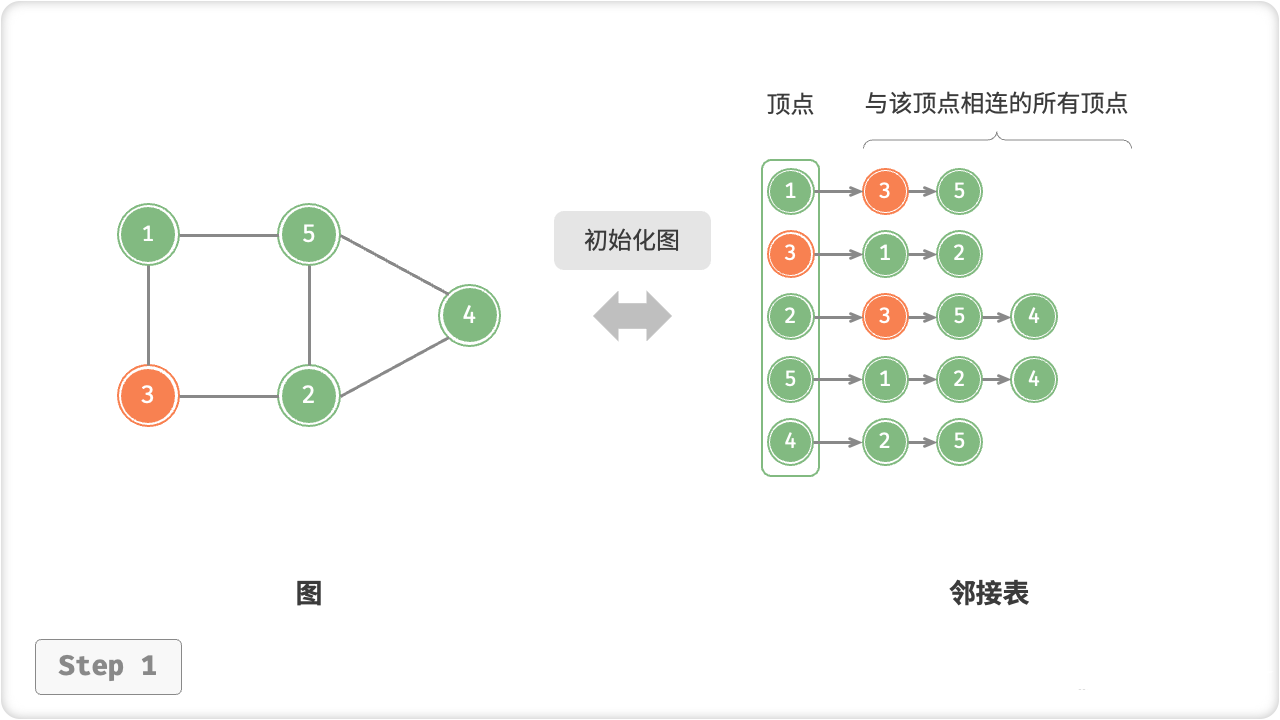
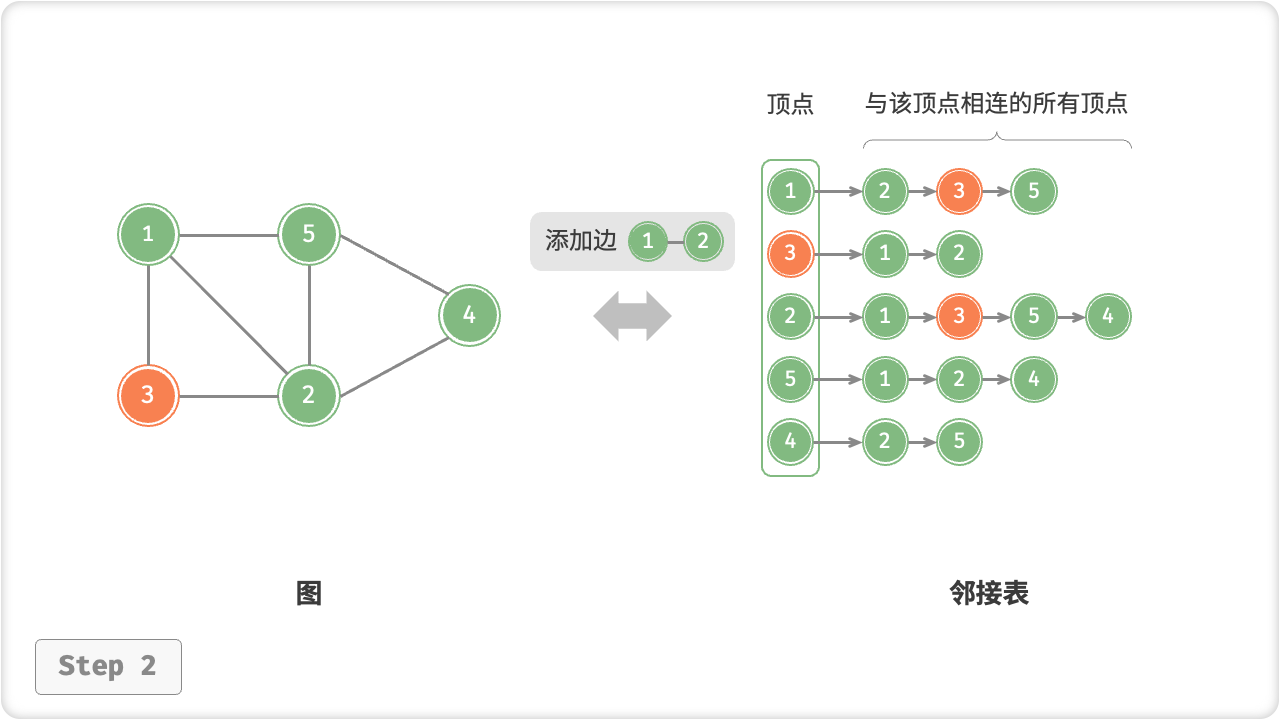
☀️1.2.2 邻接表
邻接表是一种图的表示方法,它用于存储无向图或有向图的邻接关系。在邻接表中,每个顶点v都对应一个链表,链表中存储的是与该顶点相邻的所有顶点。例如,假设有一个无向图G=(V,E),那么对于图中的每个顶点v(i),将其与相邻的顶点用链表连接起来,形成一个由v(i)和其相邻顶点集合组成的链表,就构成了该图的邻接表。邻接表通常比邻接矩阵更适用于稀疏图的表示,因为邻接表只对邻接的边进行存储,这样可以节省空间。同时,邻接表也提供了方便的遍历方法,可以快速访问所有与某个顶点相邻的顶点。
🦋1.3 图常见应用
| 顶点 边 | 图计算问题 |
|---|---|
| 社交网络 | 用户 好友关系 潜在好友推荐 |
| 地铁线路 | 站点 站点间的连通性 最短路线推荐 |
| 太阳系 | 星体 星体间的万有引力作用 行星轨道计算 |
🔎2.图的常用操作
🦋2.1 基于邻接矩阵的实现
/* 基于邻接矩阵实现的无向图类 */
class GraphAdjMat {
List<int> vertices; // 顶点列表,元素代表“顶点值”,索引代表“顶点索引”
List<List<int>> adjMat; // 邻接矩阵,行列索引对应“顶点索引”
/* 构造函数 */
public GraphAdjMat(int[] vertices, int[][] edges) {
this.vertices = new List<int>();
this.adjMat = new List<List<int>>();
// 添加顶点
foreach (int val in vertices) {
addVertex(val);
}
// 添加边
// 请注意,edges 元素代表顶点索引,即对应 vertices 元素索引
foreach (int[] e in edges) {
addEdge(e[0], e[1]);
}
}
/* 获取顶点数量 */
public int size() {
return vertices.Count;
}
/* 添加顶点 */
public void addVertex(int val) {
int n = size();
// 向顶点列表中添加新顶点的值
vertices.Add(val);
// 在邻接矩阵中添加一行
List<int> newRow = new List<int>(n);
for (int j = 0; j < n; j++) {
newRow.Add(0);
}
adjMat.Add(newRow);
// 在邻接矩阵中添加一列
foreach (List<int> row in adjMat) {
row.Add(0);
}
}
/* 删除顶点 */
public void removeVertex(int index) {
if (index >= size())
throw new IndexOutOfRangeException();
// 在顶点列表中移除索引 index 的顶点
vertices.RemoveAt(index);
// 在邻接矩阵中删除索引 index 的行
adjMat.RemoveAt(index);
// 在邻接矩阵中删除索引 index 的列
foreach (List<int> row in adjMat) {
row.RemoveAt(index);
}
}
/* 添加边 */
// 参数 i, j 对应 vertices 元素索引
public void addEdge(int i, int j) {
// 索引越界与相等处理
if (i < 0 || j < 0 || i >= size() || j >= size() || i == j)
throw new IndexOutOfRangeException();
// 在无向图中,邻接矩阵沿主对角线对称,即满足 (i, j) == (j, i)
adjMat[i][j] = 1;
adjMat[j][i] = 1;
}
/* 删除边 */
// 参数 i, j 对应 vertices 元素索引
public void removeEdge(int i, int j) {
// 索引越界与相等处理
if (i < 0 || j < 0 || i >= size() || j >= size() || i == j)
throw new IndexOutOfRangeException();
adjMat[i][j] = 0;
adjMat[j][i] = 0;
}
/* 打印邻接矩阵 */
public void print() {
Console.Write("顶点列表 = ");
PrintUtil.PrintList(vertices);
Console.WriteLine("邻接矩阵 =");
PrintUtil.PrintMatrix(adjMat);
}
}
public class graph_adjacency_matrix {
[Test]
public void Test() {
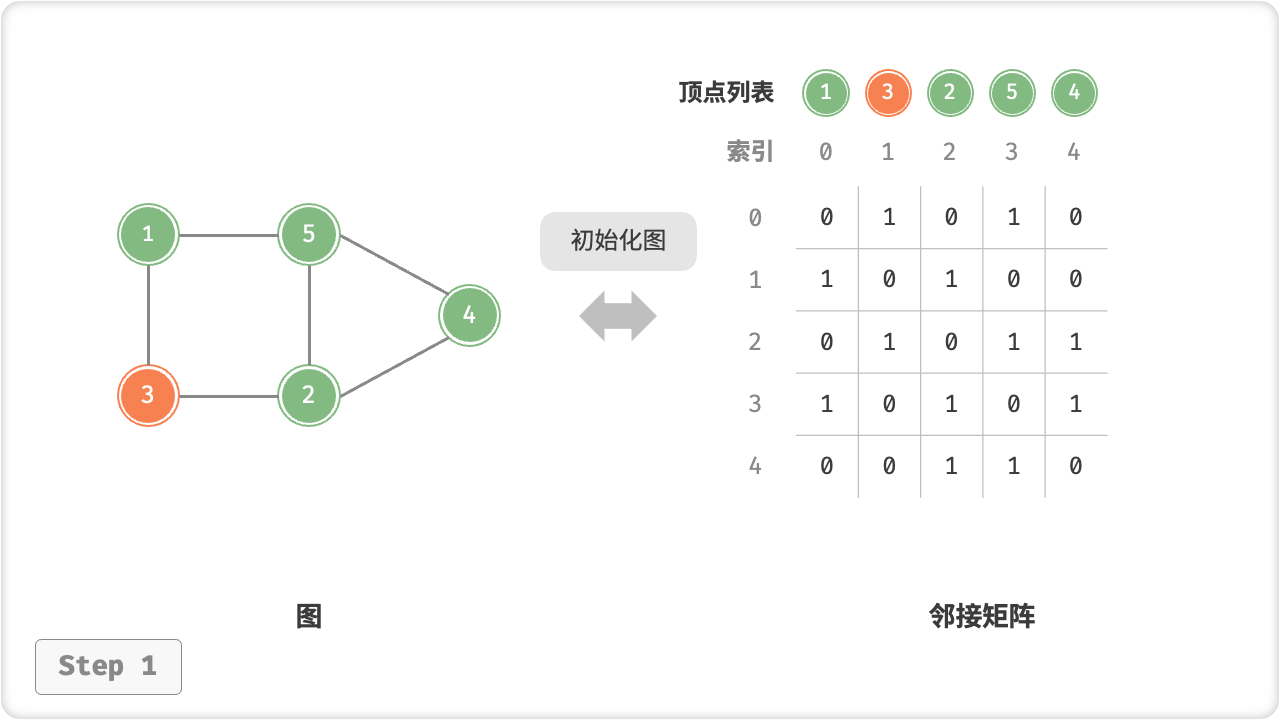
/* 初始化无向图 */
// 请注意,edges 元素代表顶点索引,即对应 vertices 元素索引
int[] vertices = { 1, 3, 2, 5, 4 };
int[][] edges = new int[][] { new int[] { 0, 1 }, new int[] { 0, 3 },
new int[] { 1, 2 }, new int[] { 2, 3 },
new int[] { 2, 4 }, new int[] { 3, 4 } };
GraphAdjMat graph = new GraphAdjMat(vertices, edges);
Console.WriteLine("\n初始化后,图为");
graph.print();
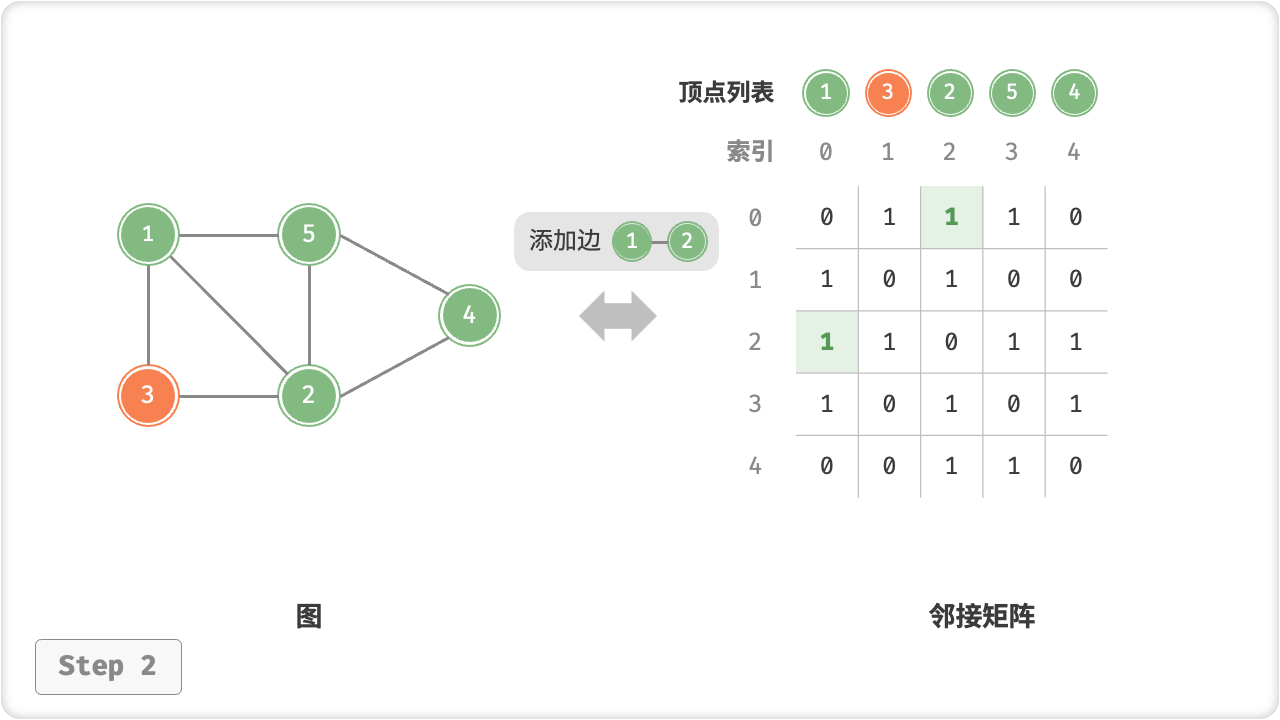
/* 添加边 */
// 顶点 1, 2 的索引分别为 0, 2
graph.addEdge(0, 2);
Console.WriteLine("\n添加边 1-2 后,图为");
graph.print();
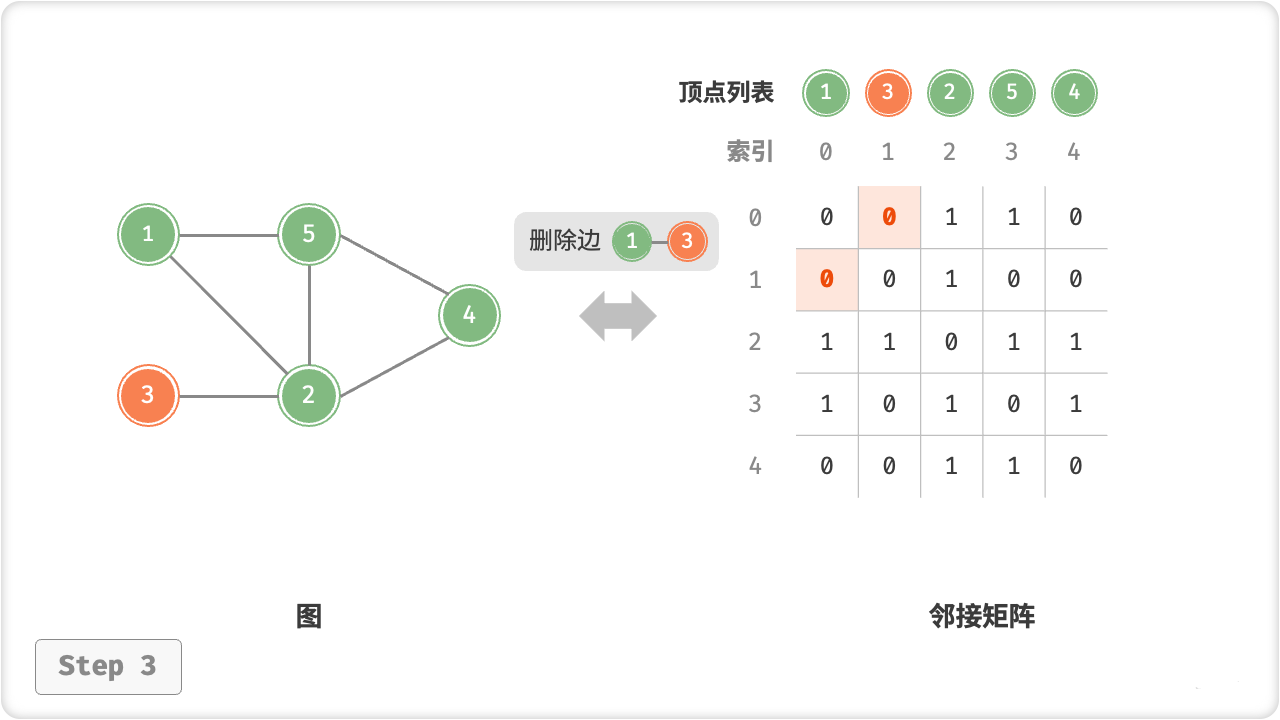
/* 删除边 */
// 顶点 1, 3 的索引分别为 0, 1
graph.removeEdge(0, 1);
Console.WriteLine("\n删除边 1-3 后,图为");
graph.print();
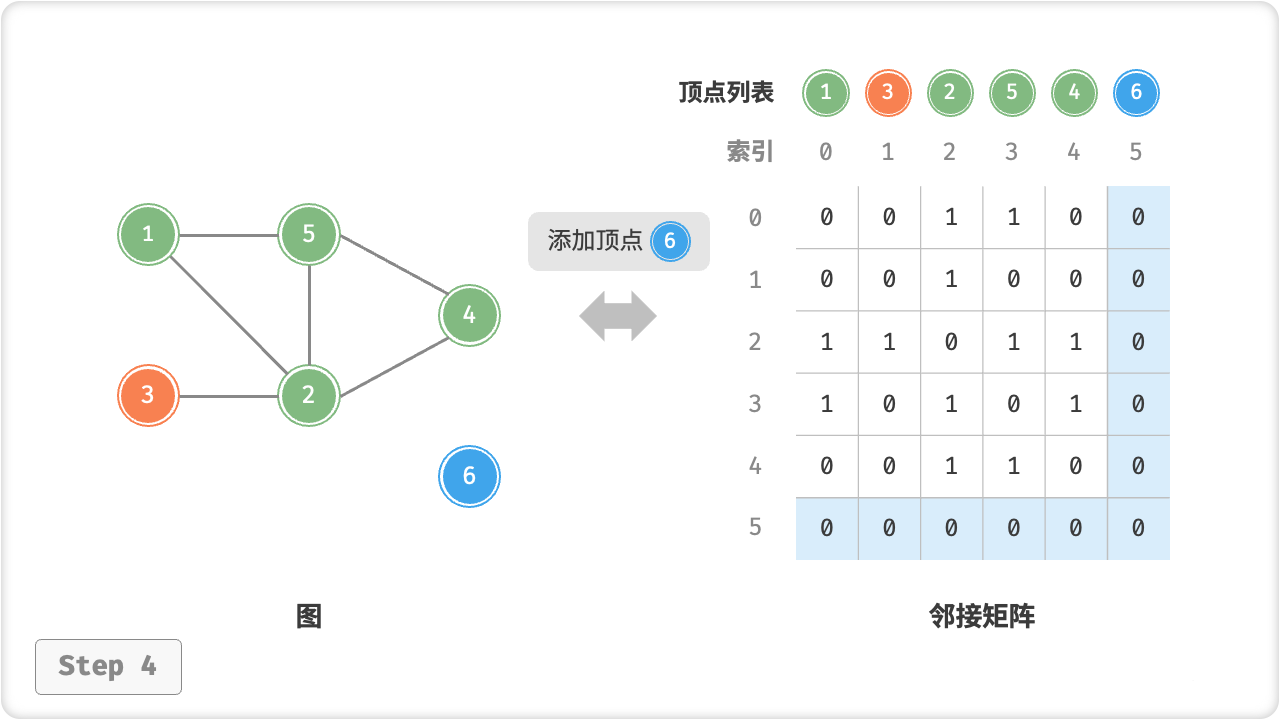
/* 添加顶点 */
graph.addVertex(6);
Console.WriteLine("\n添加顶点 6 后,图为");
graph.print();
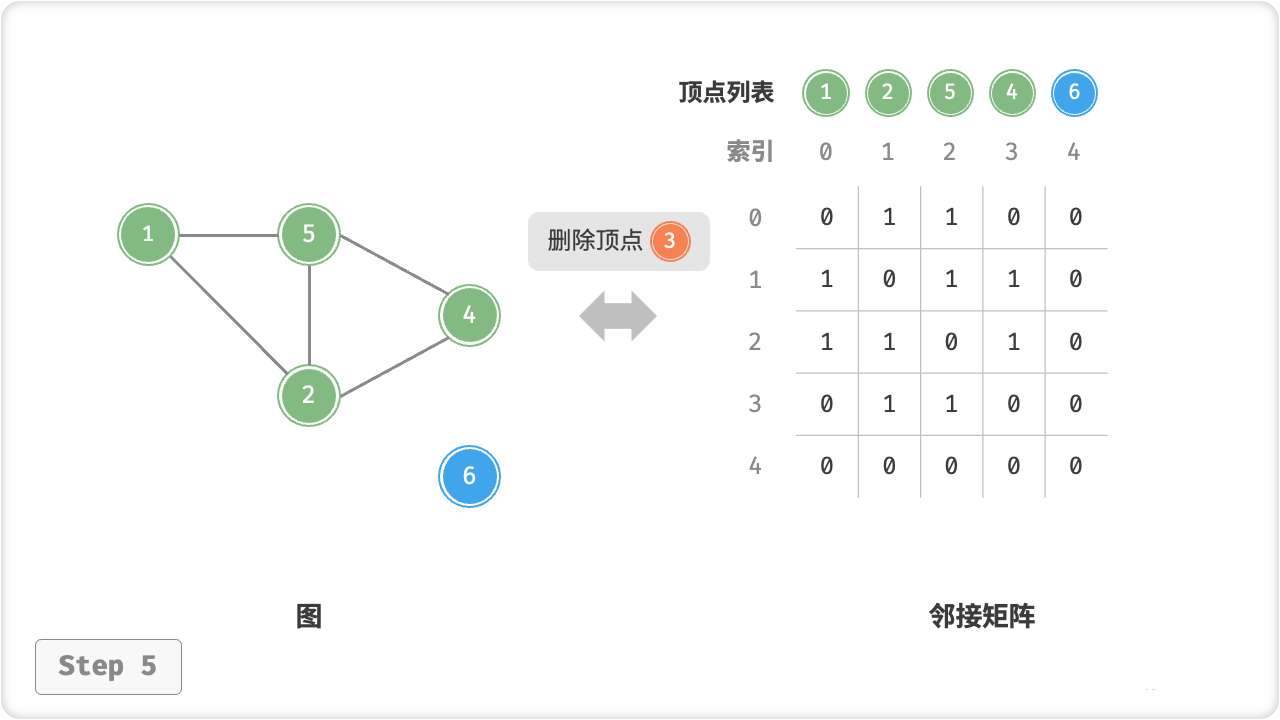
/* 删除顶点 */
// 顶点 3 的索引为 1
graph.removeVertex(1);
Console.WriteLine("\n删除顶点 3 后,图为");
graph.print();
}
}
🦋2.2 基于邻接表的实现
/* 基于邻接表实现的无向图类 */
public class GraphAdjList {
// 邻接表,key: 顶点,value:该顶点的所有邻接顶点
public Dictionary<Vertex, List<Vertex>> adjList;
/* 构造函数 */
public GraphAdjList(Vertex[][] edges) {
this.adjList = new Dictionary<Vertex, List<Vertex>>();
// 添加所有顶点和边
foreach (Vertex[] edge in edges) {
addVertex(edge[0]);
addVertex(edge[1]);
addEdge(edge[0], edge[1]);
}
}
/* 获取顶点数量 */
public int size() {
return adjList.Count;
}
/* 添加边 */
public void addEdge(Vertex vet1, Vertex vet2) {
if (!adjList.ContainsKey(vet1) || !adjList.ContainsKey(vet2) || vet1 == vet2)
throw new InvalidOperationException();
// 添加边 vet1 - vet2
adjList[vet1].Add(vet2);
adjList[vet2].Add(vet1);
}
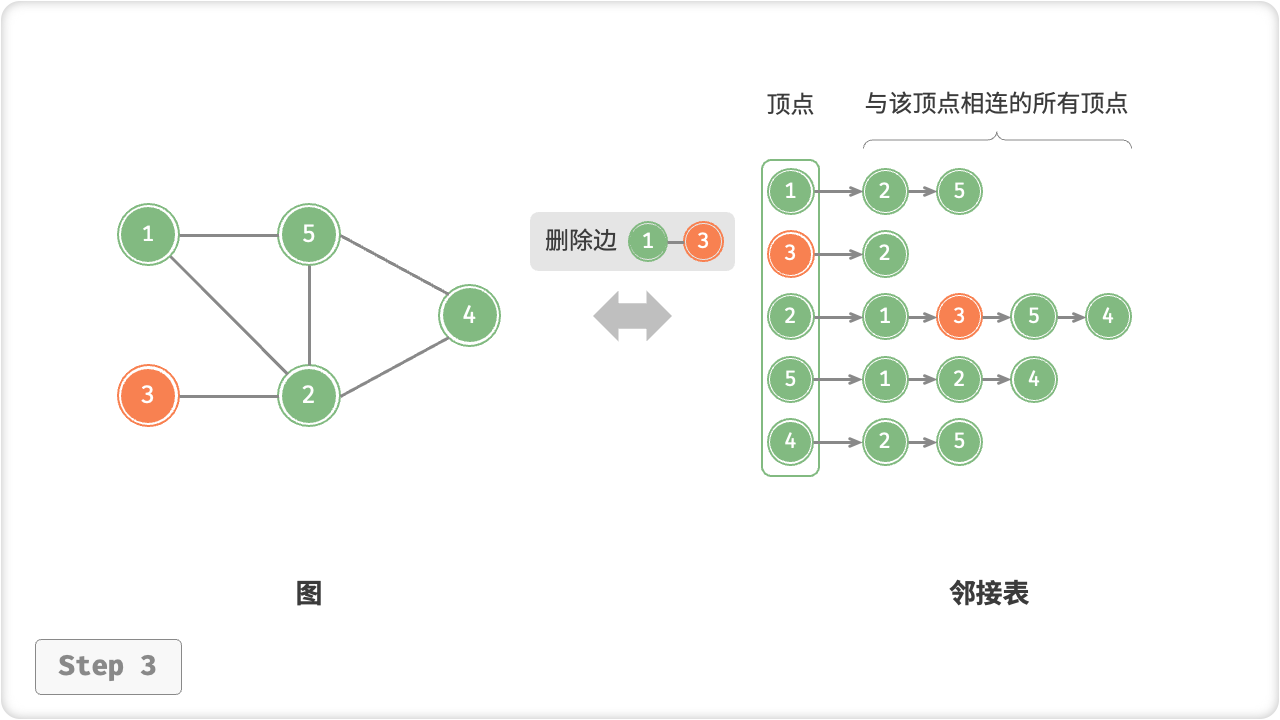
/* 删除边 */
public void removeEdge(Vertex vet1, Vertex vet2) {
if (!adjList.ContainsKey(vet1) || !adjList.ContainsKey(vet2) || vet1 == vet2)
throw new InvalidOperationException();
// 删除边 vet1 - vet2
adjList[vet1].Remove(vet2);
adjList[vet2].Remove(vet1);
}
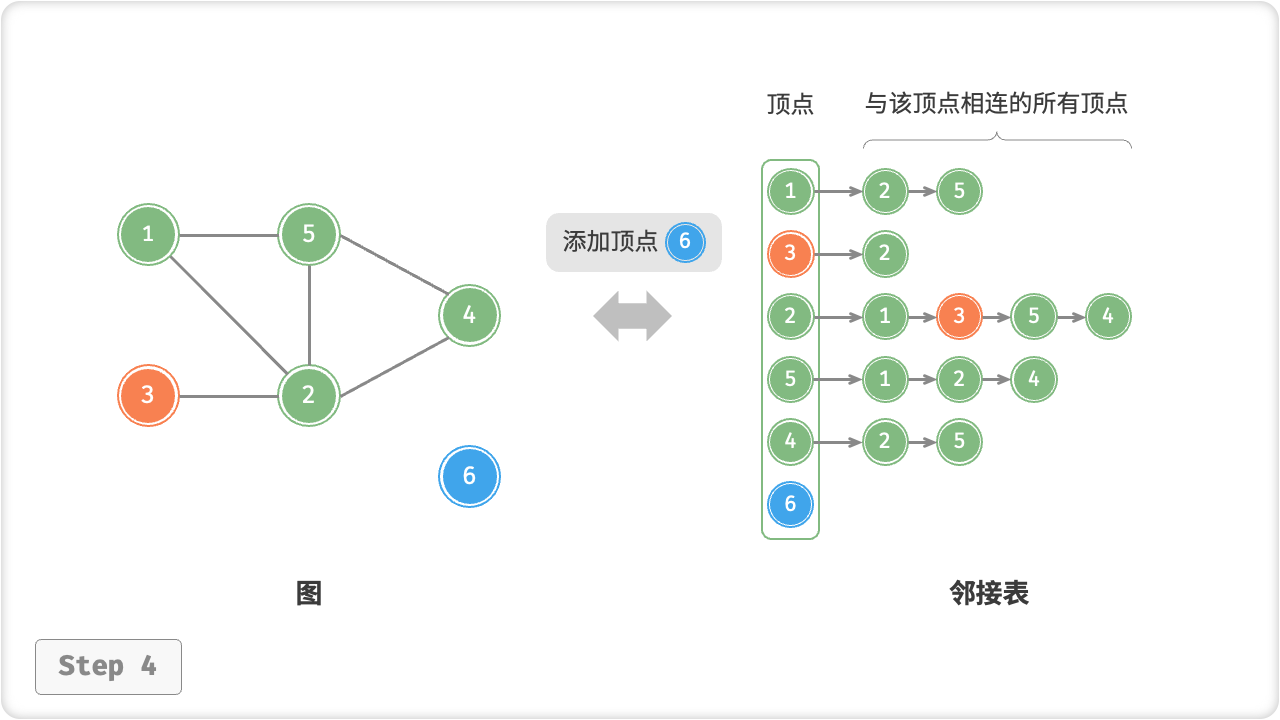
/* 添加顶点 */
public void addVertex(Vertex vet) {
if (adjList.ContainsKey(vet))
return;
// 在邻接表中添加一个新链表
adjList.Add(vet, new List<Vertex>());
}
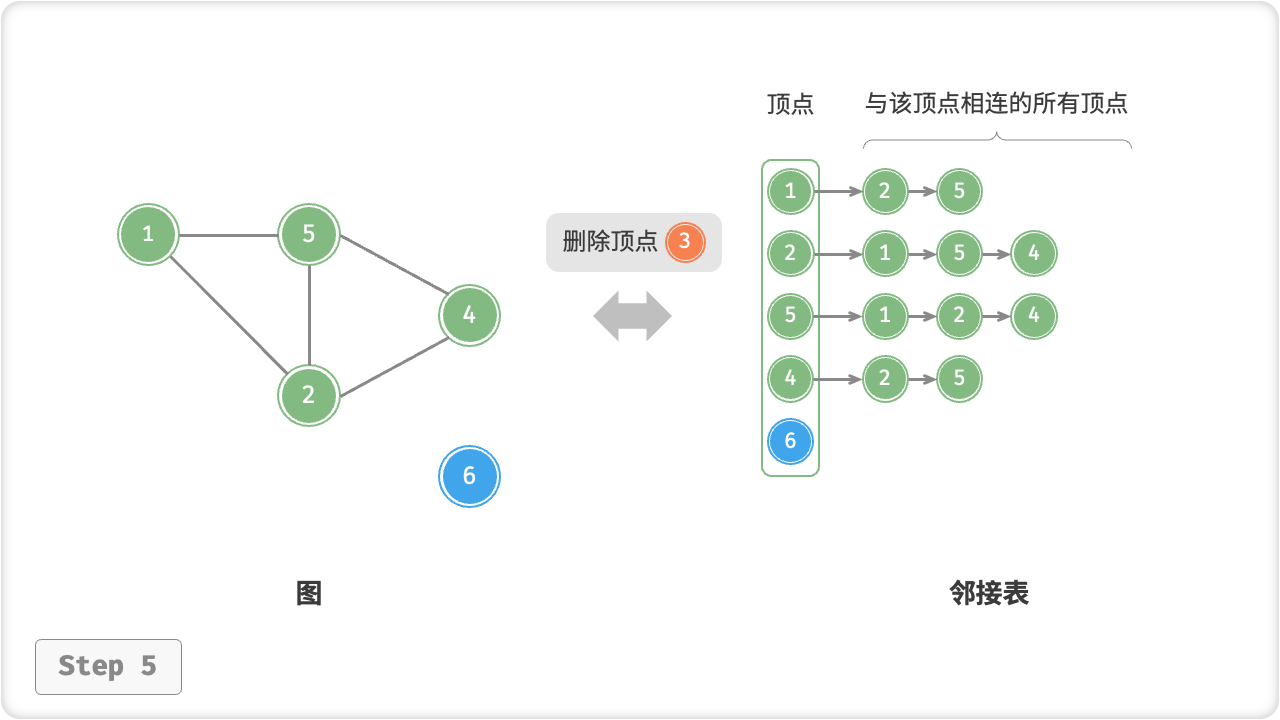
/* 删除顶点 */
public void removeVertex(Vertex vet) {
if (!adjList.ContainsKey(vet))
throw new InvalidOperationException();
// 在邻接表中删除顶点 vet 对应的链表
adjList.Remove(vet);
// 遍历其他顶点的链表,删除所有包含 vet 的边
foreach (List<Vertex> list in adjList.Values) {
list.Remove(vet);
}
}
/* 打印邻接表 */
public void print() {
Console.WriteLine("邻接表 =");
foreach (KeyValuePair<Vertex, List<Vertex>> pair in adjList) {
List<int> tmp = new List<int>();
foreach (Vertex vertex in pair.Value)
tmp.Add(vertex.val);
Console.WriteLine(pair.Key.val + ": [" + string.Join(", ", tmp) + "],");
}
}
}
public class graph_adjacency_list {
[Test]
public void Test() {
/* 初始化无向图 */
Vertex[] v = Vertex.ValsToVets(new int[] { 1, 3, 2, 5, 4 });
Vertex[][] edges = new Vertex[][] { new Vertex[] { v[0], v[1] }, new Vertex[] { v[0], v[3] },
new Vertex[] { v[1], v[2] }, new Vertex[] { v[2], v[3] },
new Vertex[] { v[2], v[4] }, new Vertex[] { v[3], v[4] } };
GraphAdjList graph = new GraphAdjList(edges);
Console.WriteLine("\n初始化后,图为");
graph.print();
/* 添加边 */
// 顶点 1, 2 即 v[0], v[2]
graph.addEdge(v[0], v[2]);
Console.WriteLine("\n添加边 1-2 后,图为");
graph.print();
/* 删除边 */
// 顶点 1, 3 即 v[0], v[1]
graph.removeEdge(v[0], v[1]);
Console.WriteLine("\n删除边 1-3 后,图为");
graph.print();
/* 添加顶点 */
Vertex v5 = new Vertex(6);
graph.addVertex(v5);
Console.WriteLine("\n添加顶点 6 后,图为");
graph.print();
/* 删除顶点 */
// 顶点 3 即 v[1]
graph.removeVertex(v[1]);
Console.WriteLine("\n删除顶点 3 后,图为");
graph.print();
}
}
🦋2.3 效率对比
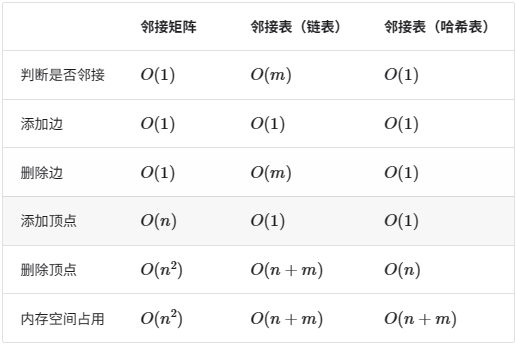
🔎3.图的遍历
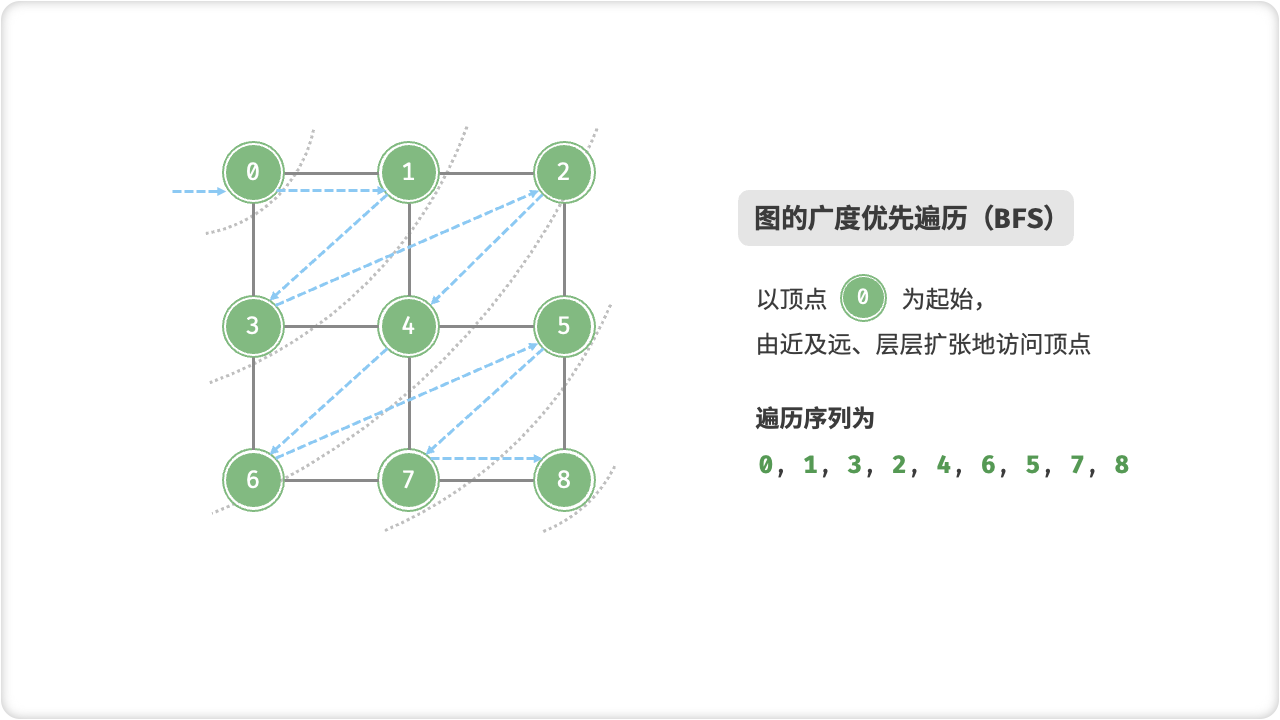
🦋3.1 广度优先遍历
图的广度优先遍历(BFS)是一种遍历图的方法,它从图的某一个顶点开始,遍历所有与这个顶点相邻的顶点,然后再遍历与这些顶点相邻的顶点……以此类推,直到图中所有可达顶点都被遍历一次。
BFS 通常使用队列来实现。首先将遍历起点入队,然后每次从队列中取出一个顶点,访问该顶点,并将该顶点的未访问过的邻居入队。这样直到队列为空,就完成了整个图的遍历。
BFS 可以用来求解最短路径问题,因为它按照距离递增的顺序遍历了所有可达顶点。当找到目标顶点时,所经过的路径即为最短路径。
public class graph_bfs {
/* 广度优先遍历 BFS */
// 使用邻接表来表示图,以便获取指定顶点的所有邻接顶点
public static List<Vertex> graphBFS(GraphAdjList graph, Vertex startVet) {
// 顶点遍历序列
List<Vertex> res = new List<Vertex>();
// 哈希表,用于记录已被访问过的顶点
HashSet<Vertex> visited = new HashSet<Vertex>() { startVet };
// 队列用于实现 BFS
Queue<Vertex> que = new Queue<Vertex>();
que.Enqueue(startVet);
// 以顶点 vet 为起点,循环直至访问完所有顶点
while (que.Count > 0) {
Vertex vet = que.Dequeue(); // 队首顶点出队
res.Add(vet); // 记录访问顶点
foreach (Vertex adjVet in graph.adjList[vet]) {
if (visited.Contains(adjVet)) {
continue; // 跳过已被访问过的顶点
}
que.Enqueue(adjVet); // 只入队未访问的顶点
visited.Add(adjVet); // 标记该顶点已被访问
}
}
// 返回顶点遍历序列
return res;
}
[Test]
public void Test() {
/* 初始化无向图 */
Vertex[] v = Vertex.ValsToVets(new int[10] { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 });
Vertex[][] edges = new Vertex[12][]
{
new Vertex[2] { v[0], v[1] }, new Vertex[2] { v[0], v[3] }, new Vertex[2] { v[1], v[2] },
new Vertex[2] { v[1], v[4] }, new Vertex[2] { v[2], v[5] }, new Vertex[2] { v[3], v[4] },
new Vertex[2] { v[3], v[6] }, new Vertex[2] { v[4], v[5] }, new Vertex[2] { v[4], v[7] },
new Vertex[2] { v[5], v[8] }, new Vertex[2] { v[6], v[7] }, new Vertex[2] { v[7], v[8] }
};
GraphAdjList graph = new GraphAdjList(edges);
Console.WriteLine("\n初始化后,图为");
graph.print();
/* 广度优先遍历 BFS */
List<Vertex> res = graphBFS(graph, v[0]);
Console.WriteLine("\n广度优先遍历(BFS)顶点序列为");
Console.WriteLine(string.Join(" ", Vertex.VetsToVals(res)));
}
}
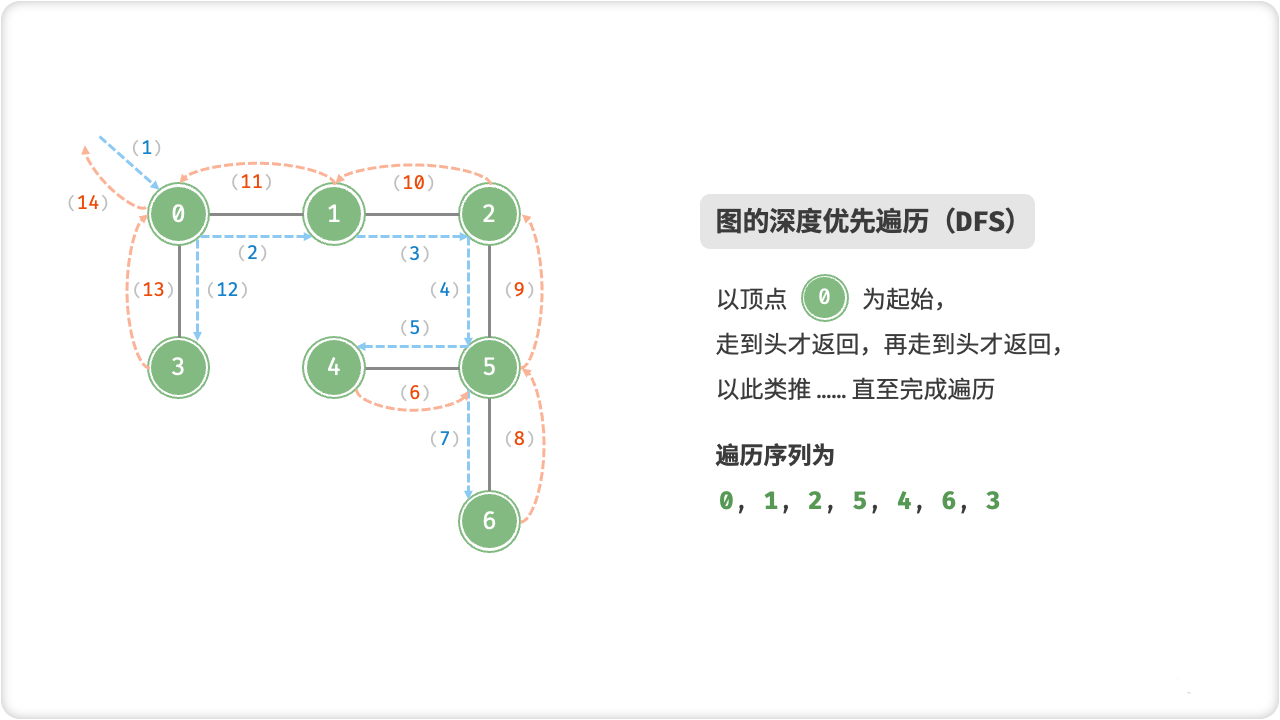
🦋3.2 深度优先遍历
图的深度优先遍历(Depth First Search,DFS)是一种遍历图的方法。这种遍历方式从一个起点开始,沿着一条路径遍历到底,直到不能继续为止,然后回溯到上一个节点,继续遍历其它路径,直到所有的节点都被访问过为止。具体实现可以用递归或栈的方式实现。
public class graph_dfs {
/* 深度优先遍历 DFS 辅助函数 */
public void dfs(GraphAdjList graph, HashSet<Vertex> visited, List<Vertex> res, Vertex vet) {
res.Add(vet); // 记录访问顶点
visited.Add(vet); // 标记该顶点已被访问
// 遍历该顶点的所有邻接顶点
foreach (Vertex adjVet in graph.adjList[vet]) {
if (visited.Contains(adjVet)) {
continue; // 跳过已被访问过的顶点
}
// 递归访问邻接顶点
dfs(graph, visited, res, adjVet);
}
}
/* 深度优先遍历 DFS */
// 使用邻接表来表示图,以便获取指定顶点的所有邻接顶点
public List<Vertex> graphDFS(GraphAdjList graph, Vertex startVet) {
// 顶点遍历序列
List<Vertex> res = new List<Vertex>();
// 哈希表,用于记录已被访问过的顶点
HashSet<Vertex> visited = new HashSet<Vertex>();
dfs(graph, visited, res, startVet);
return res;
}
[Test]
public void Test() {
/* 初始化无向图 */
Vertex[] v = Vertex.ValsToVets(new int[7] { 0, 1, 2, 3, 4, 5, 6 });
Vertex[][] edges = new Vertex[6][]
{
new Vertex[2] { v[0], v[1] }, new Vertex[2] { v[0], v[3] }, new Vertex[2] { v[1], v[2] },
new Vertex[2] { v[2], v[5] }, new Vertex[2] { v[4], v[5] }, new Vertex[2] { v[5], v[6] },
};
GraphAdjList graph = new GraphAdjList(edges);
Console.WriteLine("\n初始化后,图为");
graph.print();
/* 深度优先遍历 DFS */
List<Vertex> res = graphDFS(graph, v[0]);
Console.WriteLine("\n深度优先遍历(DFS)顶点序列为");
Console.WriteLine(string.Join(" ", Vertex.VetsToVals(res)));
}
}
🔎4.优点和缺点
图是一种非常灵活、广泛应用于现实世界中的数据结构。它的优点和缺点如下:
优点:
-
图可以表示非常复杂的数据结构和关系,能够应用于许多现实世界中的问题;
-
图能够用于建模网络结构,在社交网络分析、金融风险分析等领域有广泛应用;
-
图可以用于路线规划、最短路径搜索,比如在地图应用中,可以根据图来进行路径规划;
-
图可以用于图像处理,如在医学影像处理中,可以将人体器官等视为节点然后通过图形算法分析出病灶位置。
缺点:
- 图的数据结构较为复杂,需要花费更多的时间和精力进行建模和算法设计;
- 图的算法复杂度较高,在大规模图中会存在较大的时间和空间复杂度问题;
- 图算法在实现时需要较高的技术要求,在实际应用中可能会遇到不少困难;
- 图的可视化较为困难,在把图像展示给用户时需要进行大量的处理才能使结果清晰易懂。
🔎5.应用场景
图是一种非常常见的数据结构,在生活中有很多应用场景。以下是一些常见的图应用场景:
-
社交网络:社交网络就是一个图结构,每个用户就是一个节点,用户之间的关系就是边。通过分析这个图,可以分析出用户之间的关系、社交影响力等信息。
-
地图导航:地图导航也是一个图结构,每个道路交叉口就是一个节点,道路就是边。通过分析这个图,可以找出最优的路线。
-
网络拓扑:计算机网络中也有很多图结构,比如路由器、交换机之间的连接关系就可以用图来表示。
-
图像处理:图像处理中也会使用到图结构,比如将一张图片转换成一个图,节点就是像素点,边就是像素点之间的关系。
-
路径规划:在机器人、自动驾驶等领域中,路径规划也可以使用图结构,节点表示机器人/车辆的运动状态,边表示转移条件和成本。
-
表示键值对关系:数据库中也有很多使用图结构的应用,比如索引、关系表等。在图中,节点表示键,边表示值,可以查询和更新数据。
这些都是图在生活中的一些应用场景,图还有很多其他的应用,比如机器学习中的决策树、数据挖掘中的聚类等。
🚀感谢:给读者的一封信
亲爱的读者,
我在这篇文章中投入了大量的心血和时间,希望为您提供有价值的内容。这篇文章包含了深入的研究和个人经验,我相信这些信息对您非常有帮助。
如果您觉得这篇文章对您有所帮助,我诚恳地请求您考虑赞赏1元钱的支持。这个金额不会对您的财务状况造成负担,但它会对我继续创作高质量的内容产生积极的影响。
我之所以写这篇文章,是因为我热爱分享有用的知识和见解。您的支持将帮助我继续这个使命,也鼓励我花更多的时间和精力创作更多有价值的内容。
如果您愿意支持我的创作,请扫描下面二维码,您的支持将不胜感激。同时,如果您有任何反馈或建议,也欢迎与我分享。

再次感谢您的阅读和支持!
最诚挚的问候, “愚公搬代码”
- 点赞
- 收藏
- 关注作者


评论(0)