🏆 作者简介，愚公搬代码
🏆《头衔》：华为云特约编辑，华为云云享专家，华为开发者专家，华为产品云测专家，CSDN博客专家，阿里云专家博主，腾讯云优秀博主，掘金优秀博主，51CTO博客专家等。
🏆《近期荣誉》：2022年CSDN博客之星TOP2，2022年华为云十佳博主等。
🏆《博客内容》：.NET、Java、Python、Go、Node、前端、IOS、Android、鸿蒙、Linux、物联网、网络安全、大数据、人工智能、U3D游戏、小程序等相关领域知识。
🏆🎉欢迎 👍点赞✍评论⭐收藏

🚀前言

数据结构是计算机科学中的一个重要概念，它描述了数据之间的组织方式和关系，以及对这些数据的访问和操作。常见的数据结构有：数组、链表、栈、队列、哈希表、树、堆和图。

1. 数组（Array）：是一种线性数据结构，它将一组具有相同类型的数据元素存储在一起，并为每个元素分配一个唯一的索引。数组的特点是具有随机访问的能力。

2. 链表（Linked List）：也是一种线性数据结构，它由一系列的节点组成，每个节点包含数据和指向下一个节点的引用。链表的特点是可以动态地插入或删除节点，但访问某个节点时需要从头开始遍历。

3. 栈（Stack）：是一种后进先出（LIFO）的数据结构，它只能在栈顶进行插入和删除操作。栈通常用于实现递归算法、表达式求值和内存管理等场景。

4. 队列（Queue）：是一种先进先出（FIFO）的数据结构，它可以在队尾插入元素，在队头删除元素。队列通常用于数据的缓存、消息队列和网络通信等场景。

5. 哈希表（Hash Table）：也称为散列表，它是一种根据关键字直接访问数据的数据结构。哈希表通常由数组和散列函数组成，可以在常数时间内进行插入、删除和查找操作。

6. 树（Tree）：是一种非线性数据结构，它由一系列的节点组成，每个节点可以有若干个子节点。树的特点是可以动态地插入或删除节点，常见的树结构包括二叉树、平衡树和搜索树等。

7. 堆（Heap）：是一种特殊的树结构，它通常用于实现优先队列和堆排序等算法。堆分为最大堆和最小堆，最大堆的每个节点的值都大于等于其子节点的值，最小堆则相反。

8. 图（Graph）：是一种由节点和边组成的非线性数据结构，它可以用来表示各种实体之间的关系，如社交网络、路线图和电路图等。图的遍历和最短路径算法是常见的图算法。

🚀一、线段树

🔎1.基本思想

线段树的基本思想是将区间划分为若干个较小的区间，然后将这些小区间存储在树状结构中。通过使用线段树，我们可以有效地回答各种与区间有关的问题，例如区间最大值、区间求和等。

线段树的构建过程通常采用递归的方法。首先，将整个区间划分成两个子区间，然后递归对子区间继续进行划分，直到划分到单个元素为止。每个小区间的信息存储在一个对应的节点中，而这些节点通过父子关系组成了一棵树状结构，即线段树。

线段树的常见操作包括：查询区间信息、区间修改和单点修改。查询区间信息通常采用递归的方式，将区间不断划分为子区间，直到划分到与查询区间完全重叠或包含的小区间为止。对于修改操作，我们需要递归地修改涉及到的所有小区间，并更新父节点的信息。单点修改和区间修改的思想较为类似，都需要将修改操作递归地推至对应的叶节点，然后逐层向上传递修改后的信息。

线段树的时间复杂度通常为 O(logn)，其中 n 是区间长度。因此，线段树通常用于需要高效处理区间信息的问题。

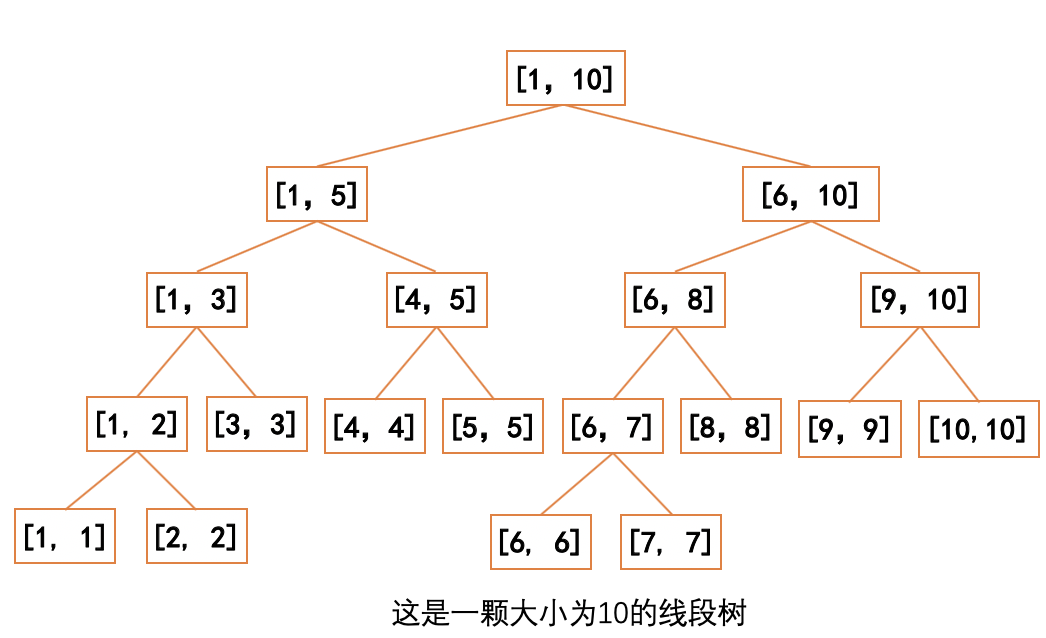
🔎2.线段树常用操作

以下是C#实现线段树的常用操作：

/// <summary>
/// 线段树:线段树是二叉树的一种,常常被用于求区间和与区间最大值等操作
/// </summary>
public class SegmentTree
{
    List<int> _orignalData = new List<int>();
    List<int?> _tree = new List<int?>();
    public SegmentTree()
    {
        for (int i = 0; i < 1000; i++)
        {
            _tree.Add(null);
        }
    }

    public void Print()
    {
        for (int i = 0; i < _tree.Count; i++)
        {
            if (_tree[i] == null)
            {
                continue;
            }
            Console.WriteLine($"第{i}:{_tree[i]}");
        }
    }


    public void Fill(List<int> data)
    {
        _orignalData = data;
        Fill(0, 0, _orignalData.Count - 1);
    }

    private void Fill(int node, int start, int end)
    {
        if (start == end)
        {
            _tree[node] = _orignalData[start];
        }
        else
        {
            int mid = (start + end) / 2;
            int leftNode = 2 * node + 1;
            int rightNode = 2 * node + 2;
            Fill(leftNode, start, mid);
            Fill(rightNode, mid + 1, end);
            _tree[node] = _tree[leftNode] + _tree[rightNode];
        }
    }

    public void Set(int index, int val)
    {
        SetValue(0, 0, _orignalData.Count - 1, index, val);
    }

    private void SetValue(int node, int start, int end, int index, int val)
    {
        if (start == end)
        {
            _orignalData[index] = val;
            _tree[node] = val;
        }
        else
        {
            int mid = (start + end) / 2;
            int leftNode = 2 * node + 1;
            int rightNode = 2 * node + 2;
            if (index >= start && index <= mid)
            {
                SetValue(leftNode, start, mid, index, val);
            }
            else
            {
                SetValue(rightNode, mid + 1, end, index, val);
            }
            _tree[node] = _tree[leftNode] + _tree[rightNode];
        }
    }


    public int? GetSum(int left, int right)
    {
        return Query(0, 0, _orignalData.Count - 1, left, right);
    }


    private int? Query(int node, int start, int end, int left, int right)
    {
        if (right < start || left > end)
        {
            return 0;
        }
        else if (left <= start && end <= right)
        {
            return _tree[node];
        }
        else if (start == end)
        {
            return _tree[node];
        }
        else
        {
            int mid = (start + end) / 2;
            int leftNode = 2 * node + 1;
            int rightNode = 2 * node + 2;
            int? sumLeft = Query(leftNode, start, mid, left, right);
            int? sumRight = Query(rightNode, mid + 1, end, left, right);
            return sumLeft + sumRight;
        }
    }
}

这里实现了线段树的构建、区间查询和区间修改操作。其中，构建操作通过递归实现，区间查询和区间修改采用类似的递归思想。可以通过传入数组 nums 构建线段树，并使用 Query 方法查询区间信息，使用 Update 方法修改区间信息。

🔎3.优点和缺点

线段树是一种基于分治思想的数据结构，主要用于解决区间查询、区间修改等问题。它具有以下优点和缺点。

优点：

1. 时间复杂度为 O(log n)，可以处理大规模数据。
2. 支持区间查询、区间修改、单点查询、单点修改等多种操作。
3. 适用于静态数据和动态数据。

缺点：

1. 空间复杂度较高，需要额外的空间存储线段树节点信息。
2. 维护线段树需要进行递归操作，容易出现栈溢出。
3. 在某些情况下，线段树的实现可能比其他数据结构更复杂。

线段树在解决区间查询、区间修改等问题时表现出色，但在一些特殊情况下可能并不是最优的选择。需要根据具体问题的特点选择合适的数据结构。

🔎4.应用场景

线段树（Segment Tree）是一种经典的数据结构，主要应用场景包括：

1. 区间查询：线段树可以方便地查询一个区间内的最大值、最小值、和、异或和、或和等，并且查询的时间复杂度为 O(logn)。

2. 区间修改：线段树可以支持单点修改和区间修改操作，时间复杂度为 O(logn)。

3. 区间覆盖：线段树可以支持区间覆盖操作，即将一个区间内的值全部替换为一个给定的值，时间复杂度为 O(logn)。

4. 区间加减：线段树可以支持区间加减操作，时间复杂度为 O(logn)。

5. 区间最值统计：线段树可以统计一个区间内出现次数最多的元素或者出现次数等于给定值的元素，时间复杂度为 O(logn)。

6. 区间离散化：线段树可以实现将一个区间内的元素进行离散化处理，时间复杂度为 O(nlogn)。

🚀感谢：给读者的一封信

亲爱的读者，

我在这篇文章中投入了大量的心血和时间，希望为您提供有价值的内容。这篇文章包含了深入的研究和个人经验，我相信这些信息对您非常有帮助。

如果您觉得这篇文章对您有所帮助，我诚恳地请求您考虑赞赏1元钱的支持。这个金额不会对您的财务状况造成负担，但它会对我继续创作高质量的内容产生积极的影响。

我之所以写这篇文章，是因为我热爱分享有用的知识和见解。您的支持将帮助我继续这个使命，也鼓励我花更多的时间和精力创作更多有价值的内容。

如果您愿意支持我的创作，请扫描下面二维码，您的支持将不胜感激。同时，如果您有任何反馈或建议，也欢迎与我分享。

再次感谢您的阅读和支持！

最诚挚的问候， “愚公搬代码”