【愚公系列】2023年12月 数据结构(六)-双向队列
🏆 作者简介,愚公搬代码
🏆《头衔》:华为云特约编辑,华为云云享专家,华为开发者专家,华为产品云测专家,CSDN博客专家,阿里云专家博主,腾讯云优秀博主,掘金优秀博主,51CTO博客专家等。
🏆《近期荣誉》:2022年CSDN博客之星TOP2,2022年华为云十佳博主等。
🏆《博客内容》:.NET、Java、Python、Go、Node、前端、IOS、Android、鸿蒙、Linux、物联网、网络安全、大数据、人工智能、U3D游戏、小程序等相关领域知识。
🏆🎉欢迎 👍点赞✍评论⭐收藏
🚀前言
数据结构是计算机科学中的一个重要概念,它描述了数据之间的组织方式和关系,以及对这些数据的访问和操作。常见的数据结构有:数组、链表、栈、队列、哈希表、树、堆和图。
-
数组(Array):是一种线性数据结构,它将一组具有相同类型的数据元素存储在一起,并为每个元素分配一个唯一的索引。数组的特点是具有随机访问的能力。
-
链表(Linked List):也是一种线性数据结构,它由一系列的节点组成,每个节点包含数据和指向下一个节点的引用。链表的特点是可以动态地插入或删除节点,但访问某个节点时需要从头开始遍历。
-
栈(Stack):是一种后进先出(LIFO)的数据结构,它只能在栈顶进行插入和删除操作。栈通常用于实现递归算法、表达式求值和内存管理等场景。
-
队列(Queue):是一种先进先出(FIFO)的数据结构,它可以在队尾插入元素,在队头删除元素。队列通常用于数据的缓存、消息队列和网络通信等场景。
-
哈希表(Hash Table):也称为散列表,它是一种根据关键字直接访问数据的数据结构。哈希表通常由数组和散列函数组成,可以在常数时间内进行插入、删除和查找操作。
-
树(Tree):是一种非线性数据结构,它由一系列的节点组成,每个节点可以有若干个子节点。树的特点是可以动态地插入或删除节点,常见的树结构包括二叉树、平衡树和搜索树等。
-
堆(Heap):是一种特殊的树结构,它通常用于实现优先队列和堆排序等算法。堆分为最大堆和最小堆,最大堆的每个节点的值都大于等于其子节点的值,最小堆则相反。
-
图(Graph):是一种由节点和边组成的非线性数据结构,它可以用来表示各种实体之间的关系,如社交网络、路线图和电路图等。图的遍历和最短路径算法是常见的图算法。
🚀一、双向队列
🔎1.基本思想
双向队列是一种具有前后端两个指针的特殊队列,可以在两端进行入队和出队操作。其基本思想是,使用两个指针指向双向队列的头尾,通过对头部和尾部的指针进行灵活的操作,实现对队列的操作。
双向队列可以在队列头部和尾部进行插入和删除操作,因此可以实现更加灵活的数据操作。比如,在需要实现“滑动窗口”这样的场景中,双向队列可以快速地进行插入和删除操作,从而快速地计算出窗口内的最大值或者最小值。
双向队列的实现方法有很多种,常用的有基于数组和基于链表的实现方法。数组实现的双向队列的优点是,支持随机访问,因此可以根据索引直接访问队列中的元素;链表实现的双向队列的优点是,可以支持动态扩容和缩容,适合于动态变化的数据。
综上所述,双向队列是一种非常实用的数据结构,可以在很多场景中灵活地应用,提高数据处理的效率和精度。

🔎2.双向队列常用操作
C#中双向队列(Deque)是一种支持在两端进行元素插入和删除操作的数据结构。常用的操作有:
- EnqueueFront(item):在队首插入元素item。
- EnqueueBack(item):在队尾插入元素item。
- DequeueFront():删除队首元素并返回其值。
- DequeueBack():删除队尾元素并返回其值。
- PeekFront():返回队首元素,但不删除。
- PeekBack():返回队尾元素,但不删除。
- Count:返回队列中元素的个数。
- Clear():清空队列中所有元素。
- Contains(item):判断队列中是否包含元素item。
- CopyTo(array, index):将队列中的所有元素复制到指定数组中的指定位置开始的位置。
示例代码:
using System.Collections.Generic;
Deque<int> deque = new Deque<int>();
deque.EnqueueFront(1);
deque.EnqueueBack(2);
deque.EnqueueBack(3);
int count = deque.Count; // count为3
int front = deque.PeekFront(); // front为1
int back = deque.PeekBack(); // back为3
deque.DequeueFront(); // 队列变为2, 3
deque.DequeueBack(); // 队列变为2
bool contains = deque.Contains(2); // contains为true
int[] array = new int[3];
deque.CopyTo(array, 0); // 数组变为2
deque.Clear(); // 清空队列中的所有元素
也可以使用LinkedList来实现双向队列
/* 初始化双向队列 */
// 在 C# 中,将链表 LinkedList 看作双向队列来使用
LinkedList<int> deque = new LinkedList<int>();
/* 元素入队 */
deque.AddLast(2); // 添加至队尾
deque.AddLast(5);
deque.AddLast(4);
deque.AddFirst(3); // 添加至队首
deque.AddFirst(1);
/* 访问元素 */
int peekFirst = deque.First.Value; // 队首元素
int peekLast = deque.Last.Value; // 队尾元素
/* 元素出队 */
deque.RemoveFirst(); // 队首元素出队
deque.RemoveLast(); // 队尾元素出队
/* 获取双向队列的长度 */
int size = deque.Count;
/* 判断双向队列是否为空 */
bool isEmpty = deque.Count == 0;
🔎3.队列的实现
🦋3.1 基于链表的实现
图解:
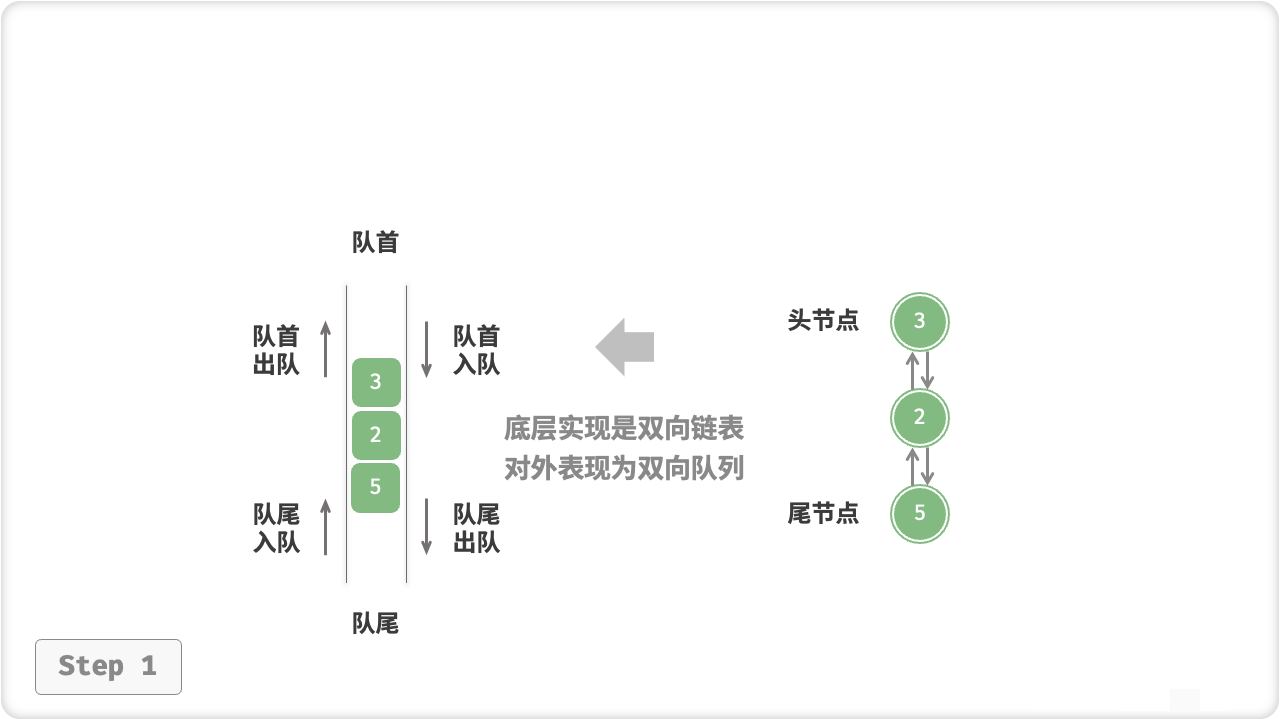
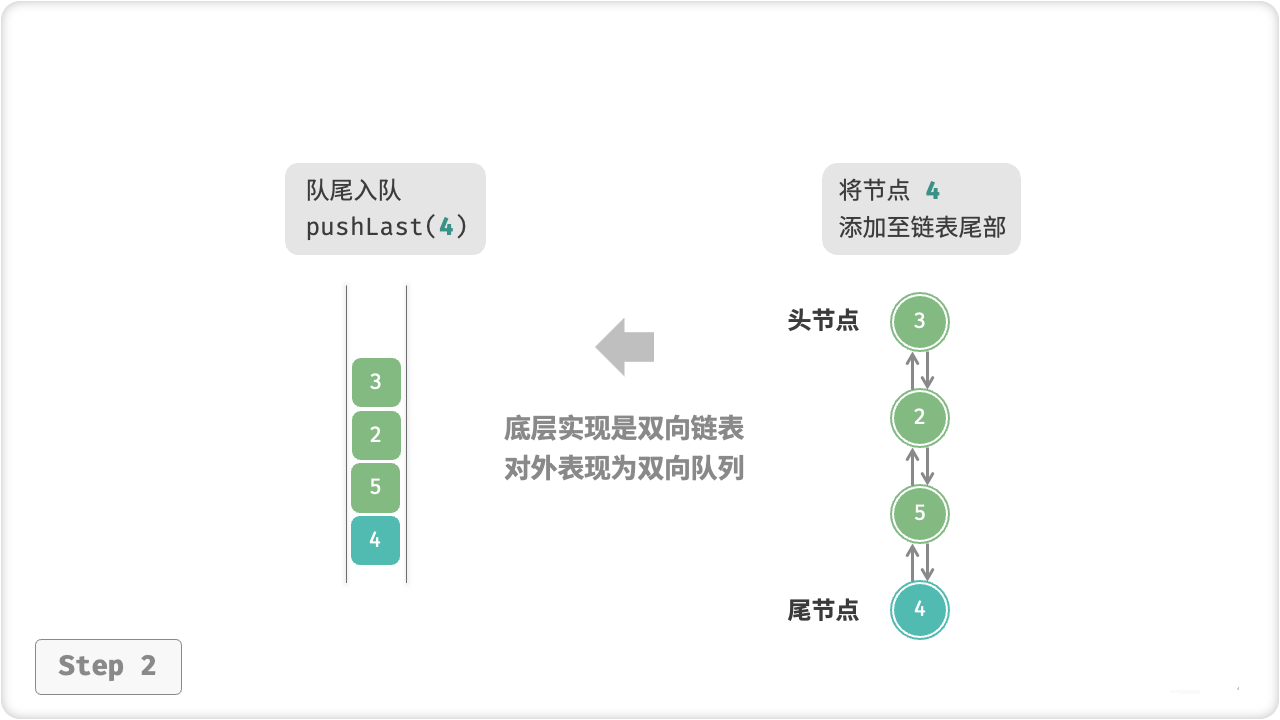
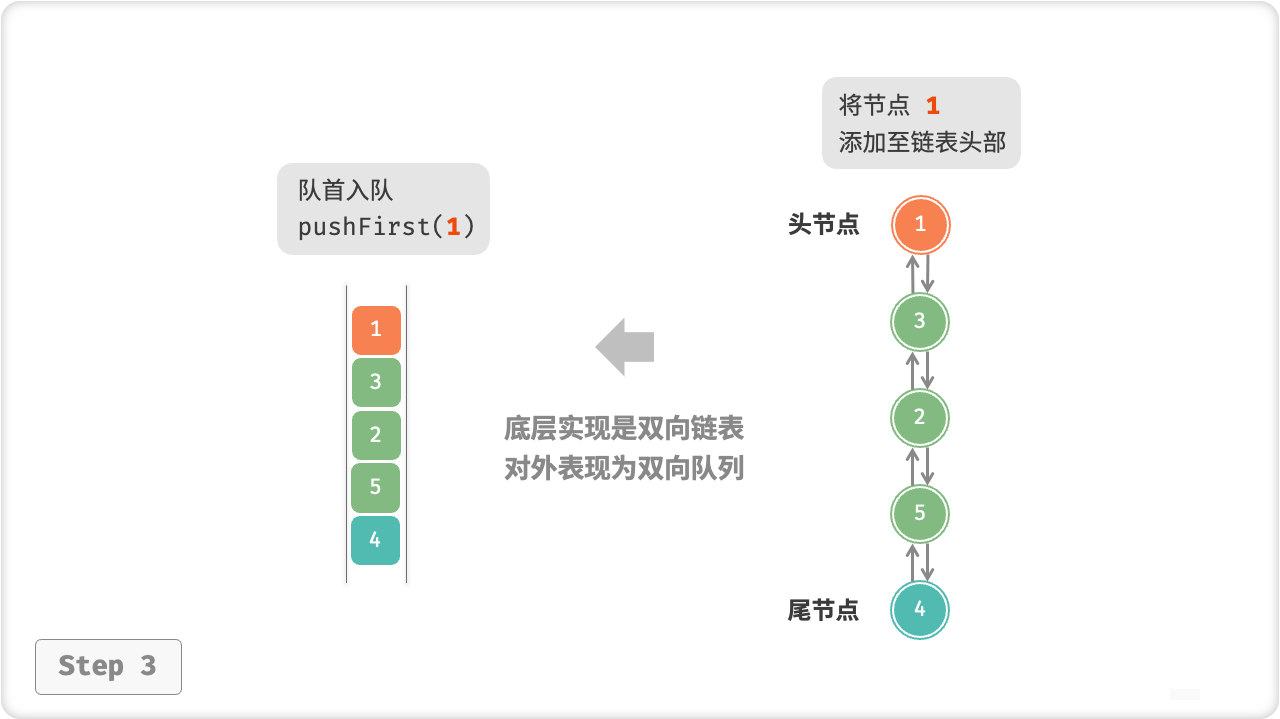
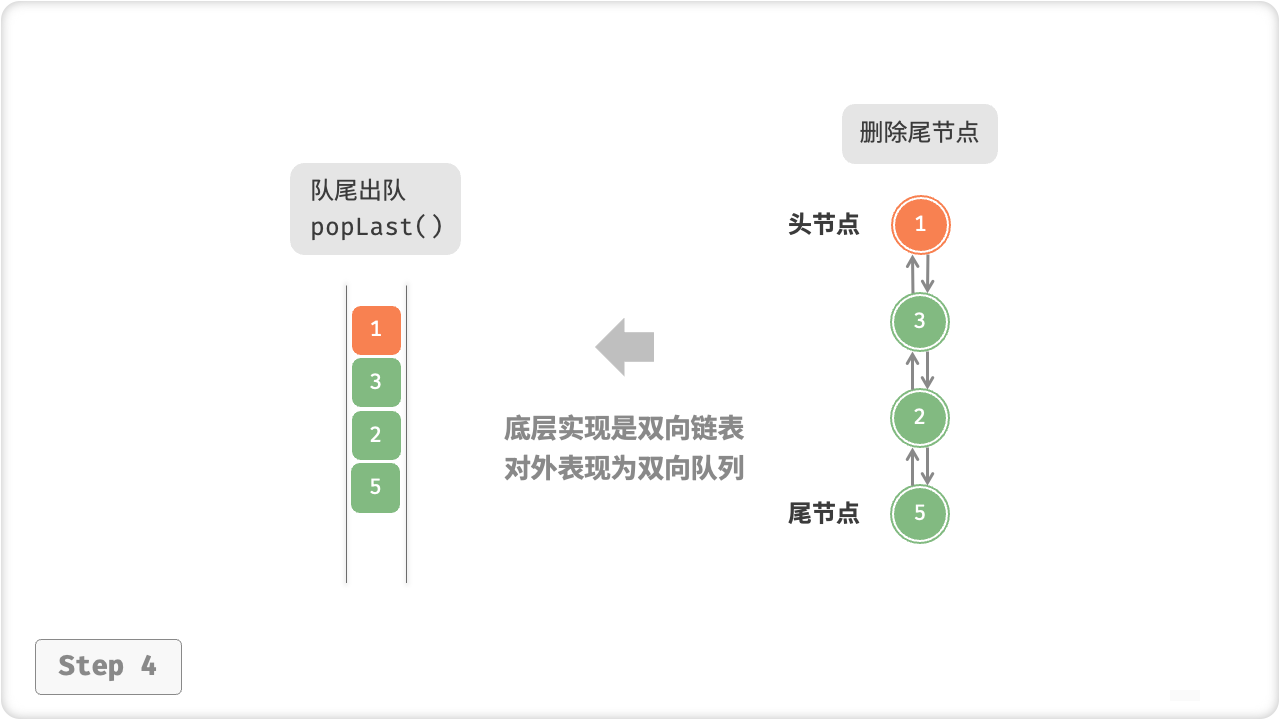
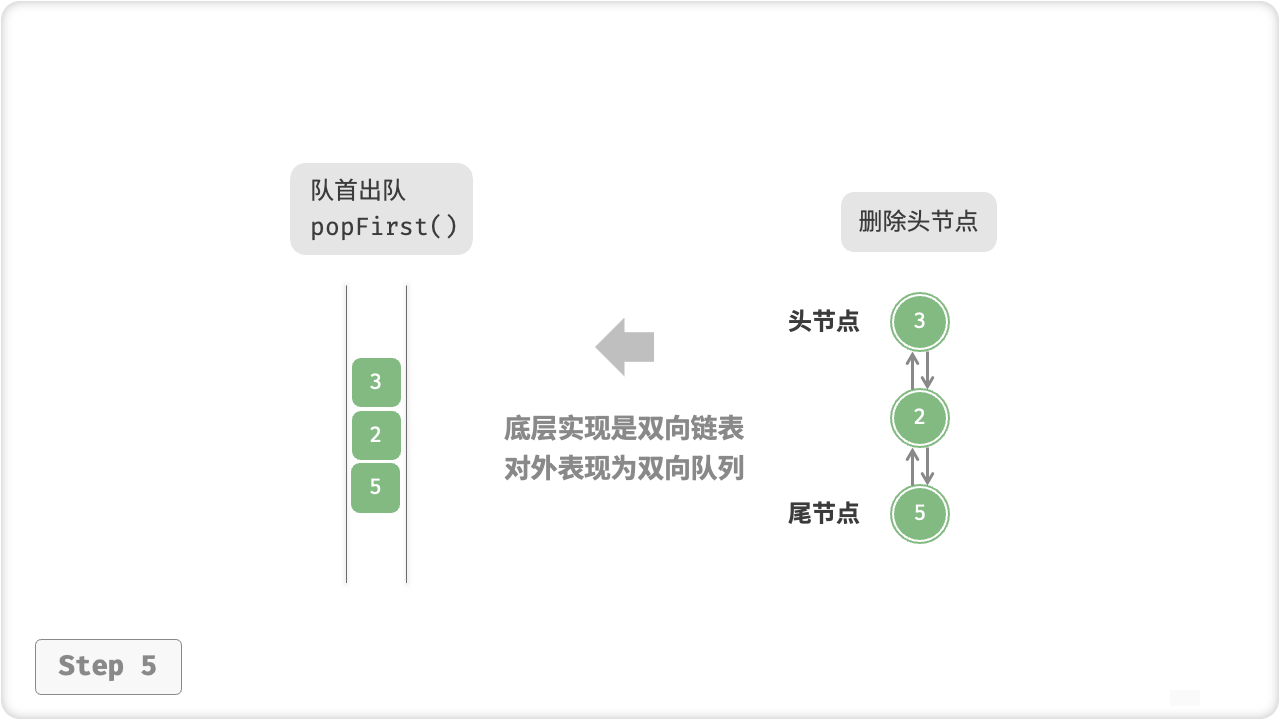
示例:
/* 双向链表节点 */
class ListNode {
public int val; // 节点值
public ListNode? next; // 后继节点引用
public ListNode? prev; // 前驱节点引用
public ListNode(int val) {
this.val = val;
prev = null;
next = null;
}
}
/* 基于双向链表实现的双向队列 */
class LinkedListDeque {
private ListNode? front, rear; // 头节点 front, 尾节点 rear
private int queSize = 0; // 双向队列的长度
public LinkedListDeque() {
front = null;
rear = null;
}
/* 获取双向队列的长度 */
public int size() {
return queSize;
}
/* 判断双向队列是否为空 */
public bool isEmpty() {
return size() == 0;
}
/* 入队操作 */
private void push(int num, bool isFront) {
ListNode node = new ListNode(num);
// 若链表为空,则令 front, rear 都指向 node
if (isEmpty()) {
front = node;
rear = node;
}
// 队首入队操作
else if (isFront) {
// 将 node 添加至链表头部
front.prev = node;
node.next = front;
front = node; // 更新头节点
}
// 队尾入队操作
else {
// 将 node 添加至链表尾部
rear.next = node;
node.prev = rear;
rear = node; // 更新尾节点
}
queSize++; // 更新队列长度
}
/* 队首入队 */
public void pushFirst(int num) {
push(num, true);
}
/* 队尾入队 */
public void pushLast(int num) {
push(num, false);
}
/* 出队操作 */
private int? pop(bool isFront) {
// 若队列为空,直接返回 null
if (isEmpty()) {
return null;
}
int val;
// 队首出队操作
if (isFront) {
val = front.val; // 暂存头节点值
// 删除头节点
ListNode fNext = front.next;
if (fNext != null) {
fNext.prev = null;
front.next = null;
}
front = fNext; // 更新头节点
}
// 队尾出队操作
else {
val = rear.val; // 暂存尾节点值
// 删除尾节点
ListNode rPrev = rear.prev;
if (rPrev != null) {
rPrev.next = null;
rear.prev = null;
}
rear = rPrev; // 更新尾节点
}
queSize--; // 更新队列长度
return val;
}
/* 队首出队 */
public int? popFirst() {
return pop(true);
}
/* 队尾出队 */
public int? popLast() {
return pop(false);
}
/* 访问队首元素 */
public int? peekFirst() {
return isEmpty() ? null : front.val;
}
/* 访问队尾元素 */
public int? peekLast() {
return isEmpty() ? null : rear.val;
}
/* 返回数组用于打印 */
public int[] toArray() {
ListNode node = front;
int[] res = new int[size()];
for (int i = 0; i < res.Length; i++) {
res[i] = node.val;
node = node.next;
}
return res;
}
}
🦋3.2 基于数组的实现表
图解:
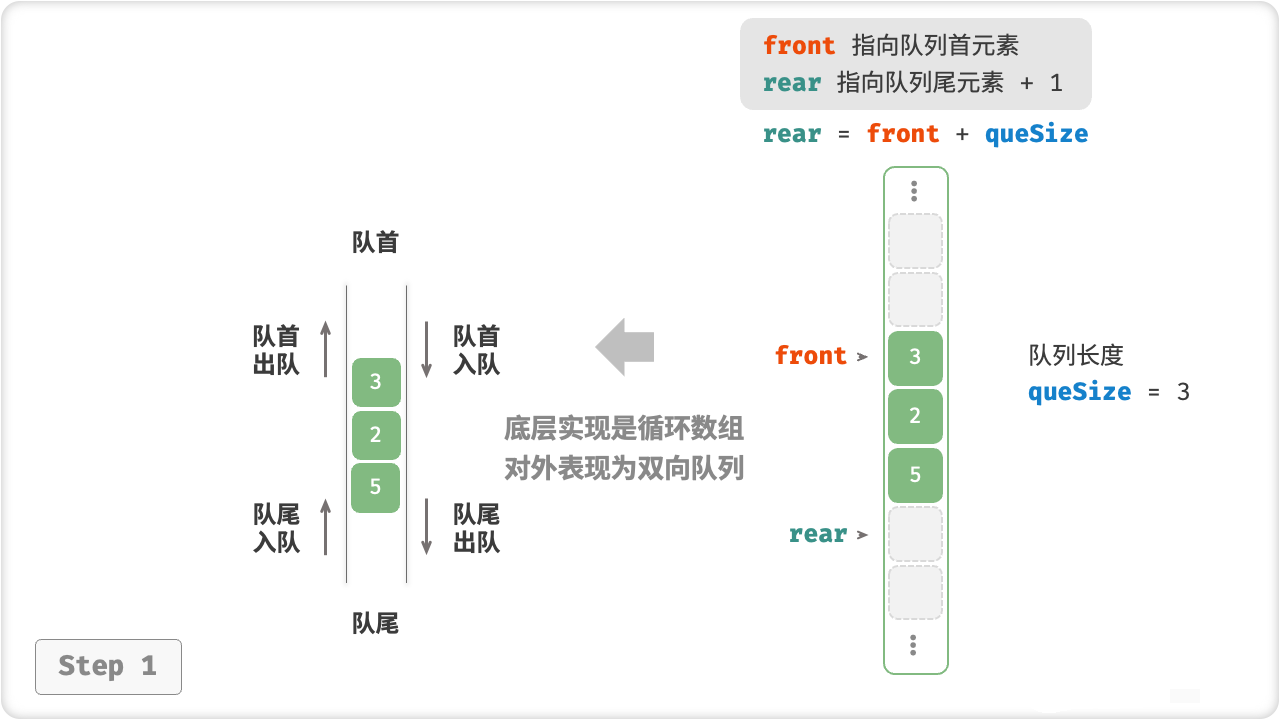
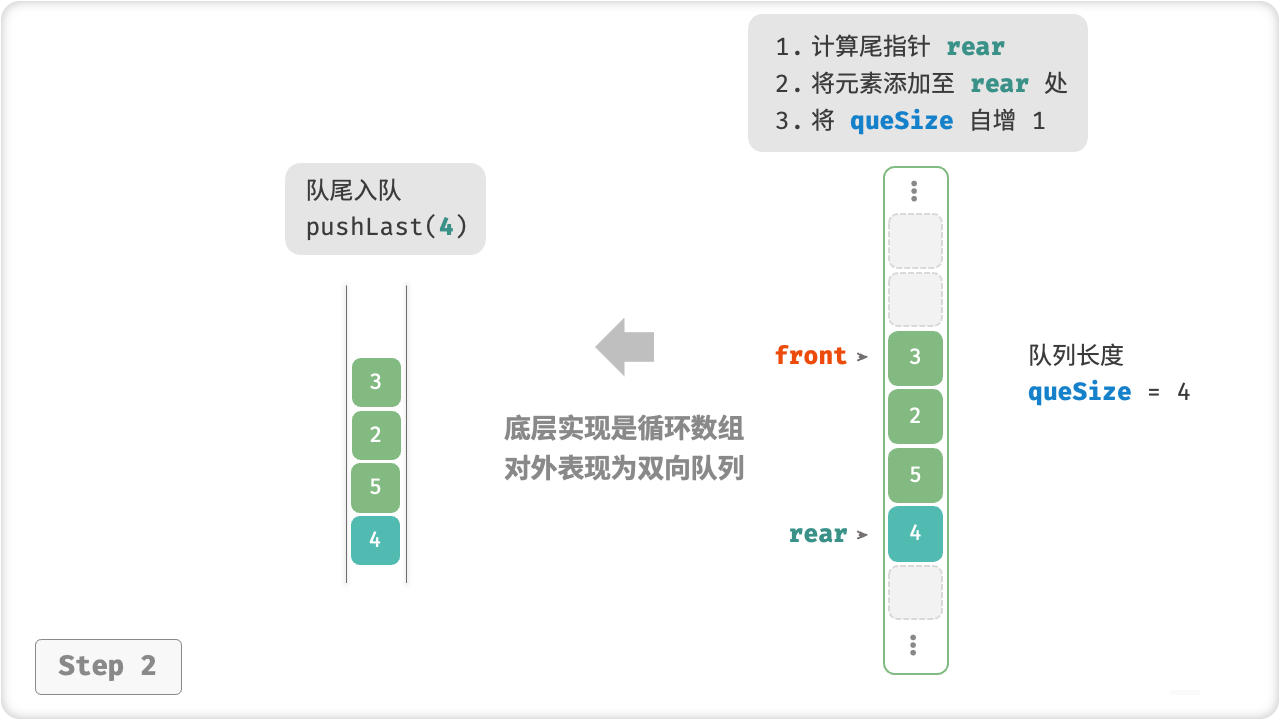
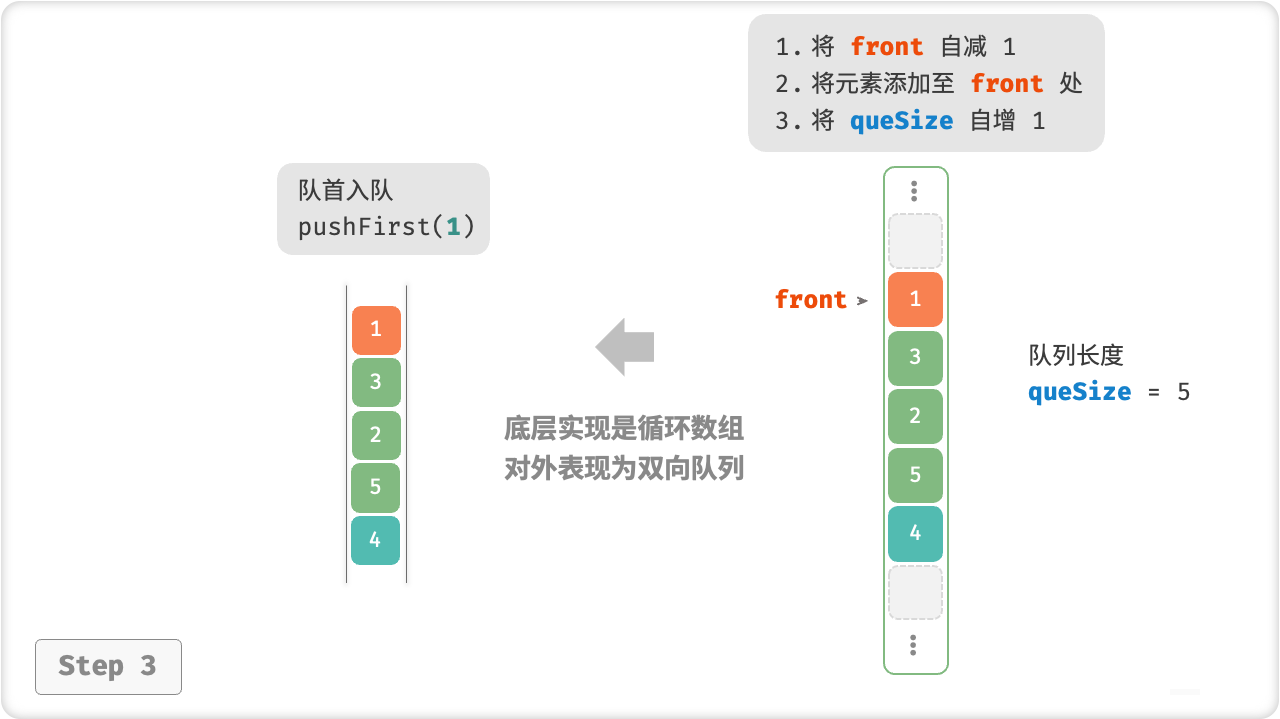
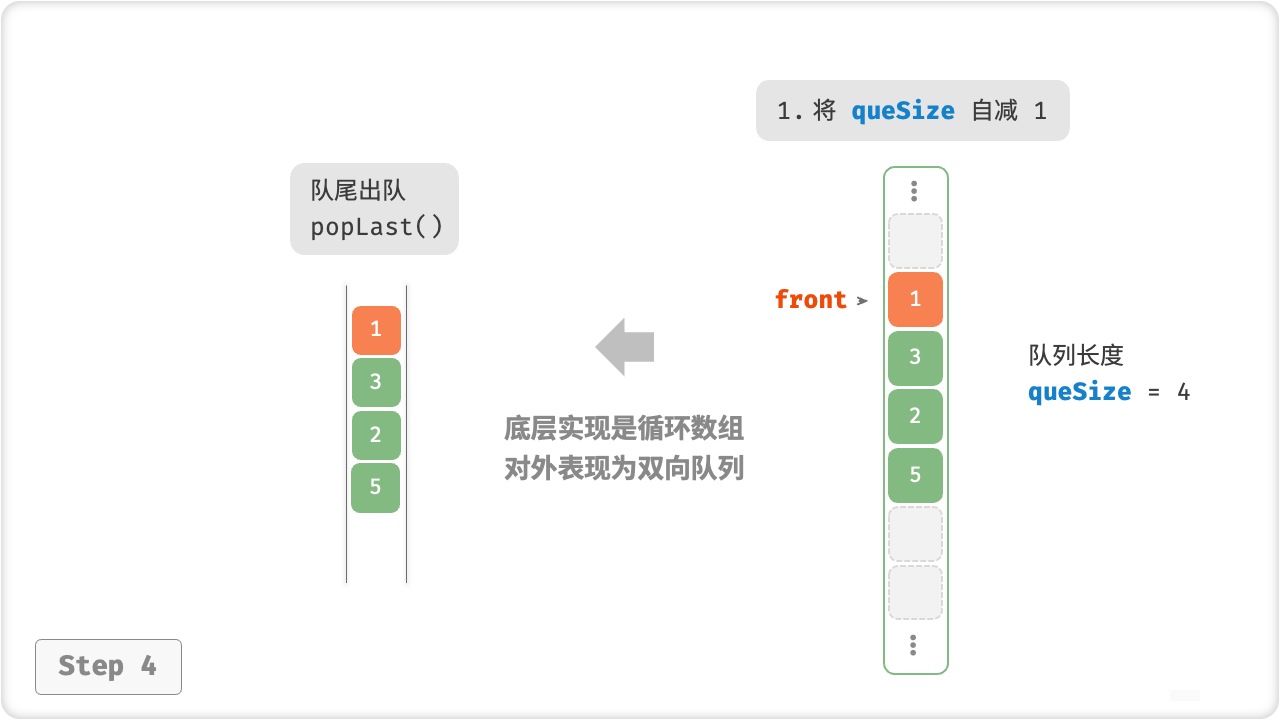
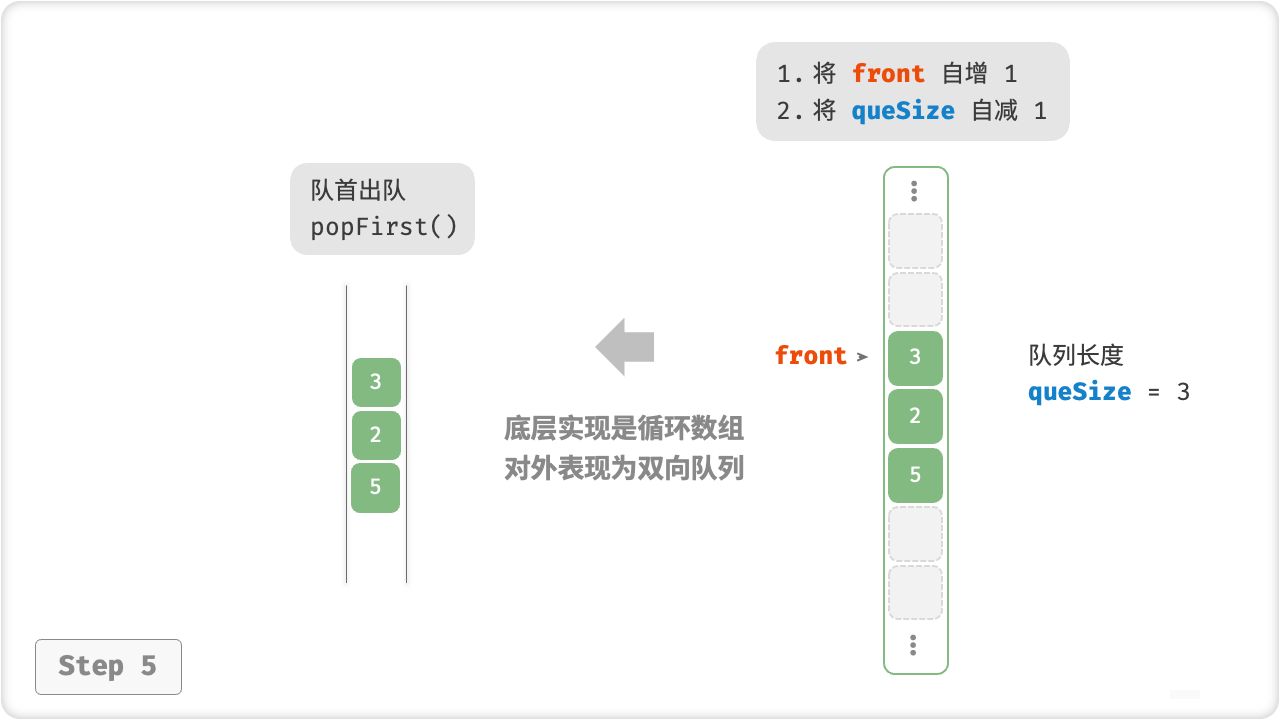
示例:
/* 基于环形数组实现的双向队列 */
class ArrayDeque {
private readonly int[] nums; // 用于存储双向队列元素的数组
private int front; // 队首指针,指向队首元素
private int queSize; // 双向队列长度
/* 构造方法 */
public ArrayDeque(int capacity) {
this.nums = new int[capacity];
front = queSize = 0;
}
/* 获取双向队列的容量 */
public int capacity() {
return nums.Length;
}
/* 获取双向队列的长度 */
public int size() {
return queSize;
}
/* 判断双向队列是否为空 */
public bool isEmpty() {
return queSize == 0;
}
/* 计算环形数组索引 */
private int index(int i) {
// 通过取余操作实现数组首尾相连
// 当 i 越过数组尾部后,回到头部
// 当 i 越过数组头部后,回到尾部
return (i + capacity()) % capacity();
}
/* 队首入队 */
public void pushFirst(int num) {
if (queSize == capacity()) {
Console.WriteLine(" 双向队列已满");
return;
}
// 队首指针向左移动一位
// 通过取余操作,实现 front 越过数组头部后回到尾部
front = index(front - 1);
// 将 num 添加至队首
nums[front] = num;
queSize++;
}
/* 队尾入队 */
public void pushLast(int num) {
if (queSize == capacity()) {
Console.WriteLine(" 双向队列已满");
return;
}
// 计算尾指针,指向队尾索引 + 1
int rear = index(front + queSize);
// 将 num 添加至队尾
nums[rear] = num;
queSize++;
}
/* 队首出队 */
public int popFirst() {
int num = peekFirst();
// 队首指针向后移动一位
front = index(front + 1);
queSize--;
return num;
}
/* 队尾出队 */
public int popLast() {
int num = peekLast();
queSize--;
return num;
}
/* 访问队首元素 */
public int peekFirst() {
if (isEmpty()) {
throw new InvalidOperationException();
}
return nums[front];
}
/* 访问队尾元素 */
public int peekLast() {
if (isEmpty()) {
throw new InvalidOperationException();
}
// 计算尾元素索引
int last = index(front + queSize - 1);
return nums[last];
}
/* 返回数组用于打印 */
public int[] toArray() {
// 仅转换有效长度范围内的列表元素
int[] res = new int[queSize];
for (int i = 0, j = front; i < queSize; i++, j++) {
res[i] = nums[index(j)];
}
return res;
}
}
🔎4.优点和缺点
双向队列(Deque)是一种具有队列和栈的特性的数据结构,可以从两端进行插入和删除元素操作。其优点和缺点如下:
优点:
- 支持在队列两端插入和删除元素,能够快速地进行队列和栈的操作。
- 可以模拟更复杂的数据结构,例如双端队列可以用来实现双端搜索、某些情况下的最短路径算法等。
- 在某些操作场景下比普通队列和栈更高效。
缺点:
- 双向队列需要使用更多内存空间来维护指针,比普通队列和栈更占内存。
- 插入和删除元素操作可能会引起指针的移动,导致时间复杂度比普通队列和栈更高。
- 双向队列难以维护某些特定的性质,例如优先队列的排序特性,需要额外的实现方式。
🔎5.应用场景
双向队列可以在以下情况下被应用:
-
在需要同时在队列的前面和后面添加或删除元素的情况下,双向队列是一个很好的选择。例如,一个任务队列,需要在队列头部添加新任务,同时在队列尾部移除已完成任务时,双向队列就非常适合。
-
双向队列常用于存储、访问和管理数据的情况下。例如,在电子表格中,用户可以通过列扩展和缩小以调整其大小,这在本质上是一个双向队列操作。
-
在计算机科学中,双向队列也被广泛用于实现优先级队列,以便迅速处理任务或查询,添加和删除操作的效率都比较高。
-
双向队列的广泛应用之一是双端搜索算法。在搜索问题中,从两端同时遍历可以得到更快的结果,双向队列实现了这一点。
🚀感谢:给读者的一封信
亲爱的读者,
我在这篇文章中投入了大量的心血和时间,希望为您提供有价值的内容。这篇文章包含了深入的研究和个人经验,我相信这些信息对您非常有帮助。
如果您觉得这篇文章对您有所帮助,我诚恳地请求您考虑赞赏1元钱的支持。这个金额不会对您的财务状况造成负担,但它会对我继续创作高质量的内容产生积极的影响。
我之所以写这篇文章,是因为我热爱分享有用的知识和见解。您的支持将帮助我继续这个使命,也鼓励我花更多的时间和精力创作更多有价值的内容。
如果您愿意支持我的创作,请扫描下面二维码,您的支持将不胜感激。同时,如果您有任何反馈或建议,也欢迎与我分享。

再次感谢您的阅读和支持!
最诚挚的问候, “愚公搬代码”
- 点赞
- 收藏
- 关注作者


评论(0)