📋 前言

  🌈hello！ 各位宝子们大家好啊，二叉树的概念大家都了解了那么我们今天就看一下
  ⛳️顺序存储究竟是怎么存储的，如何实现增删查改这些功能。
  📚本期文章收录在《数据结构&算法》，大家有兴趣可以看看呐！
  ⛺️ 欢迎铁汁们 ✔️ 点赞 👍 收藏 ⭐留言 📝！

一、堆的概念

二叉树顺序存储的最大的一个应用就是堆，也是我们后面学习堆排序以及我们日常生活中的 找大小 TOPK 问题的应用。

• 那么什么是堆呢？

堆就是由二叉树组成把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中。

• 其中他一定是一个完全二叉树或者满二叉树
• 堆中某个结点的值总是不大于或不小于其父结点的值；

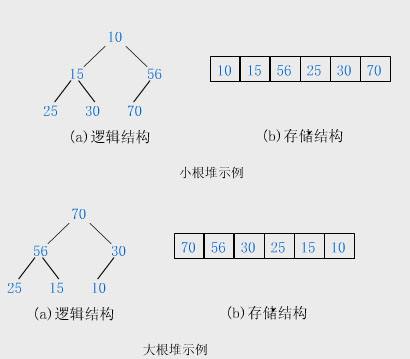
其中堆又分大堆和小堆：

• 将根结点最大的堆叫做最大堆或大根堆。
• 根结点最小的堆叫做最小堆或小根堆。

二、堆的实现

二叉树的最大应用就是“堆”，所以我们今天来看一下堆是怎么实现的他到底有什么功能呢? 他的结构到底是什么?

• 其实堆的结构和二叉树是一模一样的，只不过存储方式有差别

我们上面介绍过堆中某个结点的值总是不大于或不小于其父结点的值：

2.1 堆的结构

堆的结构很简单前面介绍的时候其实已经介绍过了：

• 我们采用数组存储的方法，使用size来记录堆的个数
• capacity来标识堆的容量

📚 代码演示：

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<string.h>

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}Heap;

2.2 堆的销毁

俗话说做题先从容易得写诶这次我们就先来从堆的销毁来写这个大家在熟悉不过了：

• 既然是动态申请的空间直接释放就好了
• 其他 数据个数 和 容量 置为零

📚 代码演示：

//堆的销毁
void HeapDestory(hp* hp)
{
	assert(hp);

	free(hp->a);
	hp->a = NULL;
	hp->size = hp->capacity = 0;
}

2.3 堆的插入

堆的插入就是本篇文章的重点了，堆的插入方式有很多比如说插入之后向上取整，或者向下取整我们选那个呢？

• 🔥 因为堆要向下取整的时候，左右子树一定要是堆
• 所以一般选取的是尾插向上取整

向上取整算法

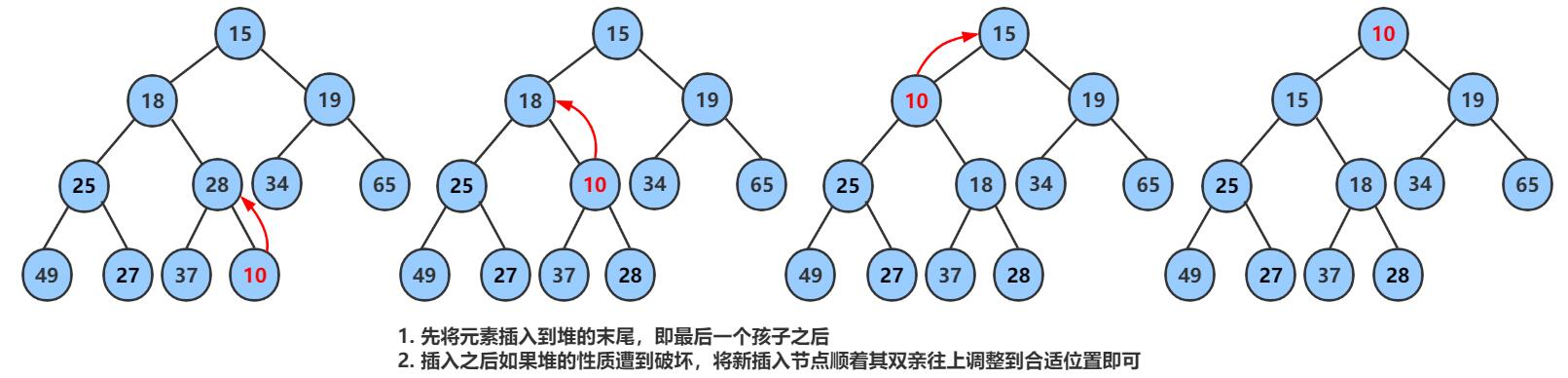
上述就是向上取整的全部流程就是拿我们插入的数据和他的 父节点 进行比较然后调整交换：

• 这里有一个特点 parent = （child-1）/ 2 ;
• 父节点等于子节点 -1 除二

所以我们可以根据这一特性来进行循环调整堆

📚 代码演示：

//向上调整
void adjustup(HeapTypeData* a, int child)
{
	int parent = (child - 1) / 2;

	while (child > 0)
	{
		//建小堆
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (parent - 1) / 2;
		}
		else
		{
			break;
		}
	}

}

这样我们不就把堆的插入OK了吗？既然建堆都会了那么插入还不简单嘛？

📑注意事项：

1. 检查容量进行扩容
2. 注意写入数据
3. 有效个数要++

📚 代码演示：

//堆的插入
void HeapPush(hp* hp, int x)
{
	assert(hp);

	if (hp->capacity == hp->size)
	{
		int newcapacity = hp->capacity * 2;
		HeapTypeData* tmp = (HeapTypeData*)realloc(hp->a, newcapacity * sizeof(HeapTypeData));
		if (tmp == NULL)
		{
			perror("realloc file");
			exit(-1);
		}

		hp->a = tmp;
		hp->capacity = newcapacity;
	}

	hp->a[hp->size] = x;
	hp->size++;

	adjustup(hp->a, hp->size - 1);
}

2.4 堆的删除

堆的删除一般我们都是删除其堆顶的数据：

• 所以一般是采用向下取整，把堆顶和堆尾进行互换然后再删除堆尾。
• 把堆顶数据向下调整

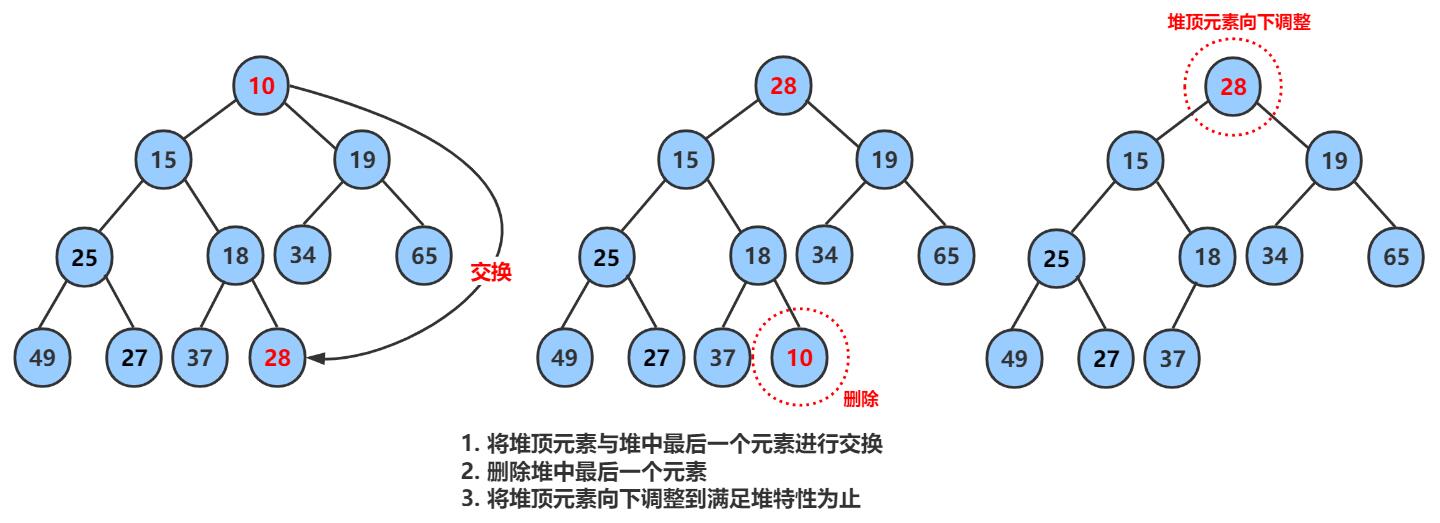
这里要控制好循环结束的条件当child < 堆的个数的时候就停止：

• 而且左孩子节点一定是 child = parent* 2+1;
  

📚 代码演示：

//向下调整
void adjustdown(HeapTypeData* a, int n, int parent)
{
	int child = parent* 2+1;

	while (child < n)
	{
		if (child+1 < n && a[child + 1] < a[child])
		{
			child++;
		}

		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent*2 +1;
		}
		else
		{
			break;
		}
	}
}

然后我们进行交换堆顶 和堆数据在进行更改有效个数

• 调整一下堆的删除就完了

📚 代码演示：

//堆的删除
void HeapPop(hp* hp)
{
	assert(hp);

	Swap(&hp->a[0], &hp->a[hp->size-1]);
	--hp->size;

	adjustdown(hp->a, hp->size, 0);

}

2.5 取堆顶的数据

这个很简单啦！直接秒杀堆顶数据，我们是从数组开头顺序存放的所以 hp->a[ 0 ]

• 数组访问就好了

📚 代码演示：

//堆顶元素
void HeapTop(hp* hp)
{
	assert(hp);
	return hp->a[0];
}

2.6 堆的数据个数

数据个数 hp->size就是用来记录有效数据个数的我们直接返回就可以了：

📚 代码演示：

//堆的数据个数
void HeapSize(hp* hp)
{
	assert(hp);

	return hp->size;
}

2.7 堆的判空

当堆的有效数据为零的时候堆就是空的

//堆的判空 
void HeapEmpty(hp* hp)
{
	assert(hp);

	return hp->size == 0;
}

📝全篇总结

☁️ 好了以上就是全部的建堆代码啦，大家快去实践起来吧！
看到这里了还不给博主扣个：
⛳️ 点赞☀️收藏 ⭐️ 关注！
💛 💙 💜 ❤️ 💚💓 💗 💕 💞 💘 💖
拜托拜托这个真的很重要！
你们的点赞就是博主更新最大的动力！
有问题可以评论或者私信呢秒回哦。