时间序列预测问题是一类常见的数据分析问题。数据中往往包含时间标签，这类问题往往根据过去一段时间的数据，建立能够比较精确地反映序列中所包含的动态依存关系的数学模型，并对未来的数据进行预测。

01、问题描述及数据挖掘目标

本案例给出二战时期的某气象站温度记录值，通过分析之前的天气状况来预测将来天气情况。与回归分析模型进行预测不同，时间序列模型依赖于事件发生的先后顺序预测接下来的输出模型的结果，改变输入值的先后顺序对模型产生不同的结果。相较于前两个案例，该案例探索时间序列数据的分析方式。

02、数据导入和预处理

导入数据处理阶段使用的库函数，numpy和pandas用于数据处理；matplotlib和seaborn用于可视化操作：

In[1]:import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

使用pandas库的read_csv函数导入数据，示例代码中的csv路径和本地csv路径保持一致。

In[2]:
weather data = pd.read csv("../data/2/Summary of weather.csv"

由于数据集已经经过数据清洗，数据预处理过程简单。我们可以直接观察数据的信息：

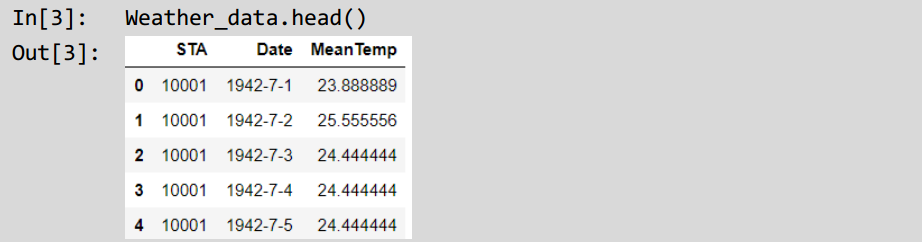
观察可知，数据由3个特征构成，其中STA表示气象台站号，Date表示气象台测量温度的日期和MeanTemp表示测量的平均温度值。由于STA表示不同地区气象站，因此我们随机挑选MAISON BLANCHE地区来进行时序分析来观察当地温度随时间的变化，其中横轴表示时间，纵轴表示温度：

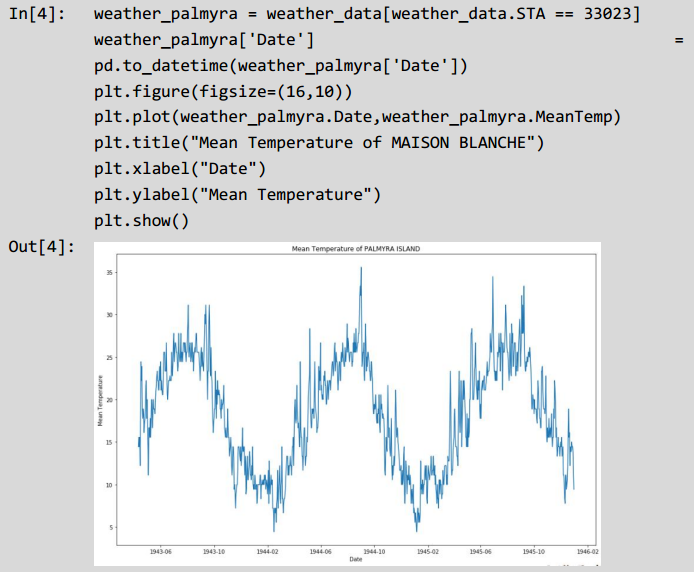
 观察图像，该时间序列可能是一个平稳序列，平稳序列是存在某种周期性、季节性和趋势的方差和均值不随着时间变化的序列。与基于线性回归模型的假设不同，时序序列的观察结果不是相互独立的。

03、数据探索

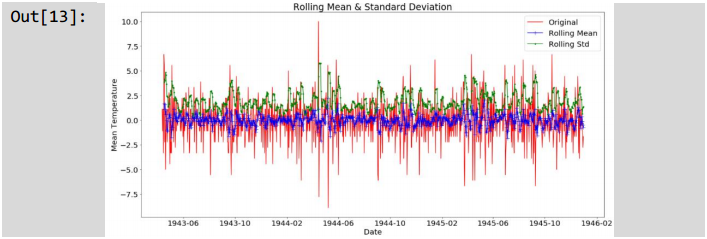
数据可视化效果表明MAISON BLANCHE地区的时间序列具有季节性，每年的夏季平均气温高，冬季平均气温低。现在检测该时间序列是否为平稳序列，可以采用以下两种方法来检查稳定性：1) 绘制滚动平均数和滚动方差，观察数据是否随着时间变化；2) 使用迪基-福勒检验来检查数据稳定性，测试结果由测试统计量和置信区间的临界统计值组成，如果“测试统计量”少于“临界值”，该时间序列是稳定的。我们下面会依次介绍这两种方法。首先，从原始数据中创建时间序列类型数据。

In[5]:
timeSeries = weather_palmyra.loc[:,["Date","MeanTemp"]]
timeSeries.index = timeSeries .Date
timeSeries = timeSeries.drop("Date",axis=1)

随时间的变化，对数据的滚动平均数和滚动方差进行可视化表示，观察数据的变化趋势。代码如下面所示。

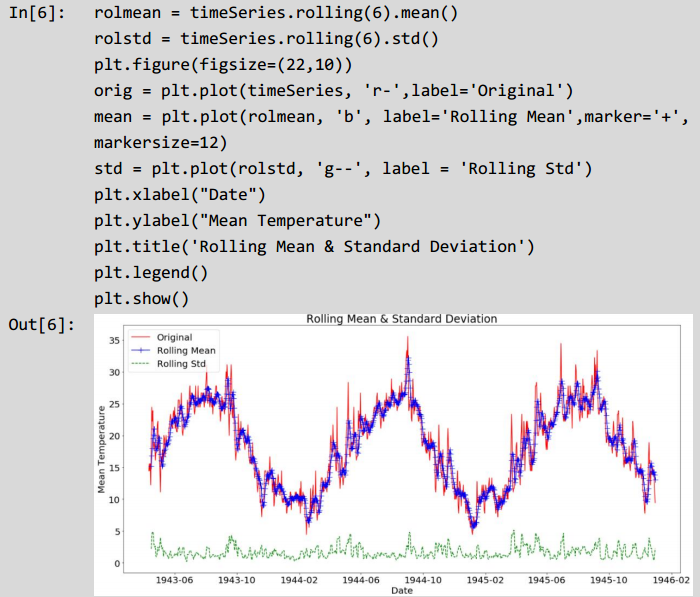
上述代码计算滚动平均数和滚动方差时，使用6个时间点的数据进行计算。时序序列稳定性的第一个标准是稳定的均值，如图滚动平均值的曲线所示，均值不是恒定的数值；第二个标准是恒定的方差，如图滚动方差的曲线所示，方差是恒定的数值。上述信息可以判定该时间序列数据不稳定，为了验证的完整性，仍然加上迪基-福勒检验来检测时间序列的完整性，迪基-福勒检验即测试一个自回归模型是否存在单位根，从而帮助判断序列是否平稳。判断代码如下面所示。

In[7]:
from statsmodels .tsa.stattools import adfuller
res = adfuller(timeSeries .MeanTemp, autolag='AIC')
print('Test statistic: %.4f; p-value: %.4f%(res[o], res[1]))
print("Critical Values: ",res[4])
Out[7]:
Test statistic: -1.9031; p-value: .3306
CriticalValues:'1%':-3 4369994999319355  5%：-2.8644757356011743，10% : -2.56833313274278037}

 由于检验统计量大于临界值的5%，时间序列数据不是稳定序列数据。综上所述，可以确定时间序列数据是不稳定的。上述分析可知，该时间序列数据为非平稳序列数据，将该时间序列数据转换成平稳时间序列，常用的方法是差分法和滚动平均法。差分法是采用一个特定时间差内数据的差值来表示原始时间数据，能够处理序列数据中的趋势和季节性。滚动平均法是用一组最近的实际数据来预测未来数据的方法，该方法能够保证时间序列数据随时间变化产生稳定的均值。在这里，check_DF函数表示迪基-福勒检验，check_mean_std函数表示检测数据的滚动均值和滚动方差平稳性。

In[8]: defcheck DF(timeSeries):
res = adfuller(timeSeries .MeanTemp, autolag='AIC')
print('Test statistic:%.4f;p-value: %.4f'%(res[e],res[1]))
print("Critical Values: ",res[4])
defcheck mean std(timeSeries)
:rolmean = timeSeries.rolling(6).mean()
rolstd = timeSeries.rolling(6).std()
plt.figure(figsize=(22,10))
orig = plt.plot(timeSeries,r-',label='Original')
mean=plt.plot(rolmean,"b',label='Rolling Mean',marker='+"markersize=1)std=plt.plot(rolstd,'g',label = 'Rolling Std',marker='o'
markersize=3)
plt.xlabel("Date")plt.ylabel("Mean Temperature")
plt.title('Rolling Mean & Standard Deviation')
plt.legend()
plt.show()

1） 采用一阶差分处理时间序列数据，时序间隔为1。

In[9]: timeSeries diff = timeSeries - timeSeries.shift(periods=1)

上述代码对时间序列数据做一阶差分处理，得到数据增量，消除数据波动。因此，可视化该时间序列数据的增量。

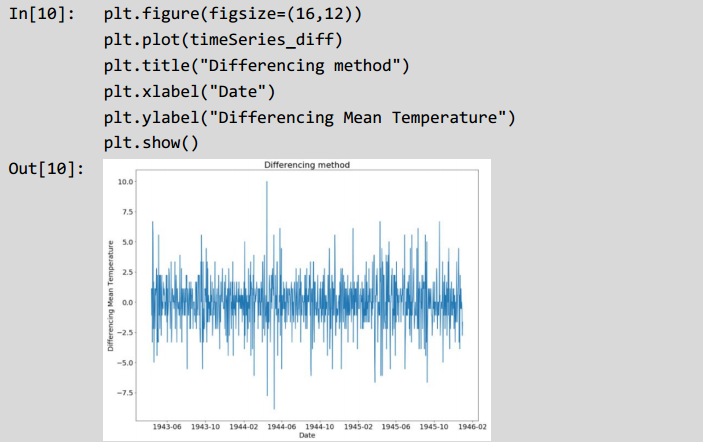
在滚动差值的计算过程中，会产生nan值，需要丢弃该部分数据进行进一步分析。

In[11]: timeSeries diff = timeSeries - timeSeries.shift(periods=1)

       对时间序列数据进行一阶差分后，观察数据的滚动均值和滚动方差是否平稳，并对数据进行迪基-福勒检验，观察整个数据是否时序平稳。

In[12]:check DF(timeSeries diff)
0ut[12]:CriticalValues :
Test statistic:-15.4648; p-value: .0000
-3.4369994990319355
['1%':
5%':
-2.8644757356011743， 10%': -2.56833313274278031

检测统计量小于1% 的临界值，因此有99% 把握认为时间序列为平稳序列。

观察滚动平均值和滚动方差，可以发现平均值和方差是稳定的。上述检验过程证明了做了差分操作之后，原始时间序列数据变成平稳时间序列数据。

2） 采用移动平均法处理时间序列数据，滚动平均的窗口为5。

移动平均是一种平滑技术，通过消除时间序列中的周期变动和不规则波动的影响，以便看出时间序列中的总体发展趋势(即趋势线)，然后结合趋势线分析序列的长期趋势。移动平均的计算公式为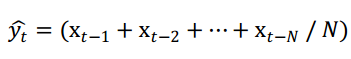

，即前N个窗口内的数据平均值。该样例中采用的窗口数为5，对于不同窗口数N，预测效果不一样。

In[14]:
timeSeries moving diff = timeSeries.rolling(5).mean()
plt.figure(figsize=(16,12))
plt.plot(timeSeries, color = "r",label = "Original")
plt.plot(timeSeries moving avg,color='b',label="moving avg mean")
plt.title("Mean Temperature of Maison Blanche")
plt.xlabel("Date")
plt.ylabel("Mean Temperature"）
plt.legend()
plt.show()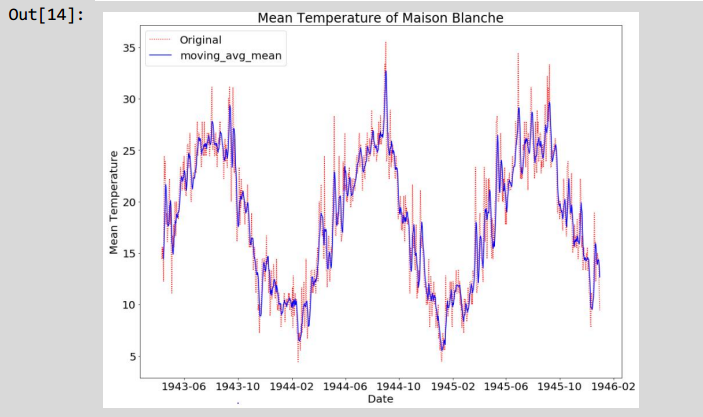

 输出图像的实线表示的是滚动平均值数量，时间间隔为5个月，因此计算第五个月数值时才计算出一个滚动平均值，前4个月没有滚动平均值。和前面差分法处理过程类似，代码如下所示。

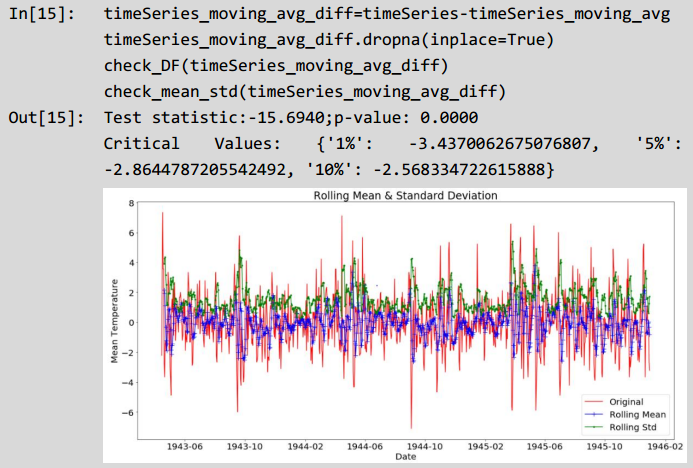
观察滚动平均值和滚动方差，可以发现平均值和方差是稳定。同时数据通过迪基-福勒检验，发现经过移动平均法后的数据能够保证数据的时序稳定性。

04、模型构建

在数据探索部分，我们使用了差分法和移动平均法来消除时间序列数据中的趋势和季节性问题。运用前面学到消除数据趋势性的方法，使用ARIMA算法进行时间预测，ARIMA模型的基本思想是将非平稳时间序列转化为平稳时间序列。其中包含三个部分，1)自回归函数(AR)条件(p)：自回归条件表示因变量的滞后值，例如当p=2时，使用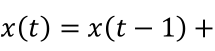

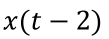
；2) 差分值(d)：非时序性的差值，对其取一阶差分，对应值d=0；3) 移动平均数(MA)条件(q)：MA项表示预测方程的滞后预测误差。

ARIMA模型选择p、d和q参数，使用自相关函数(ACF)分析相距k个时间间隔的序列值之间的相关性，偏自相关函数(PACF)相距k个时间间隔的序列值之间的相关性的同时，考虑间隔之间的值。自相关和偏自相关用于测量时间序列数值之间的相关性，并指示预测将来最有用的序列值。自相关函数决定q值，并且偏自相关函数决定p值。接下来进行ACF和PACF分析。

In[16]:
from statsmodels.tsa.stattools import acf, pacf，ARIMA
acf = acf(timeSeries diff,nlags=20)
pacf = pacf(timeSeries diff, nlags=20, method='ols')
plt.figure(figsize=(22,10))
len ts = len(timeSeries diff)
plt.subplot(121)
plt.plot( acf)
plt.axhline(y=0,ls='--',color='gray')plt.axhline(y=-1.96/np.sqrt(len ts),ls='--',color='gray')
plt.axhline(y=1.96/np.sqrt(len ts),ls='--',color='gray')plt.title('ACF')
plt.subplot(122)
plt.plot( pacf)plt.axhline(y=0,ls='--',color=gray')
plt.axhline(y=-1.96/np.sqrt(len ts),s='--',color='gray'
plt.axhline(y=1.96/np.sqrt(len ts),s='--',color='gray')
plt.title('PACF')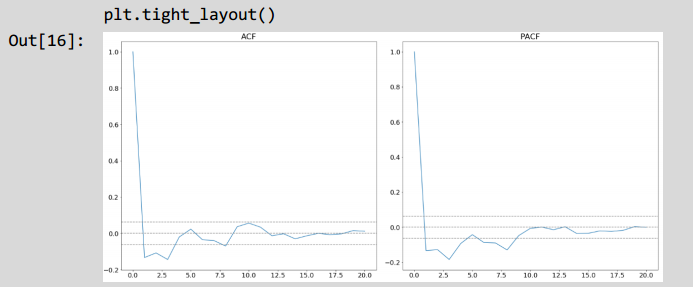

 ACF和PACF中的两条相邻虚线之间为置信区间，当PACF第一次越过上置信区间滞后值确定p的大小，如图所示p=1；当ACF第一次越过上置信区间滞后值确定q的大小如图所示q=1，因此该ARIMA模型采用的p=1，d=0和q=1作为参数进行预测。

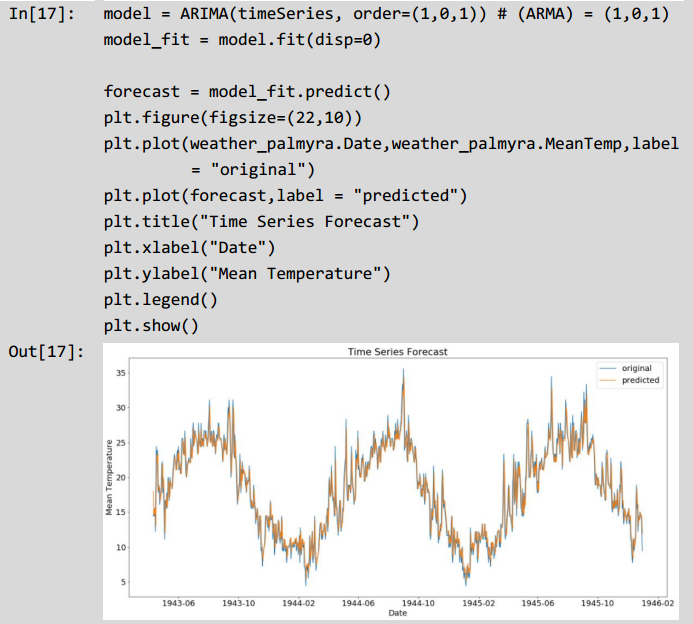
如图中两条曲线所示，通过ARIMA模型，我们能够从原始的非平稳的时间序列数据预测出未来时间序列中的数据。为了直观的表现出模型的效果，可以直接预测一段时间的天气值。

In[18]:
data = timeSeries.MeanTemp.values.tolist()
train_data, test_data = data[:-5],
 data[-5:]for t in range(len(test data)):
model = ARIMA(train_data,order=(1,0,1))
model fit = model.fit(disp=@)
output = model fit.forecast()yhat = output[0]obs = test data[t]
train data.append(obs)
Out[18]:
print('predicted=%f，expected=%f' % (yhat，obs))
predicted=14.961205，expected=14.444444predicted=14.665928,expected=14.444444predicted=14.616089，expected=13.888889predicted=14.164753expected=11.111111predicted=11.872587，expected=9.444444

观察可知，预测结果和真实值的差值不大，使用ARIMA时间预测算法能够拟合时间序列模型的数据。