数学( math )在计算机科学中的应用非常广泛,是程序设计的一门辅助学科,有人这样说过:“一切计算机问题终归于数学问题!”,而数论是一个非常庞大的数学分支,对于程序设计来说很重要,但它不是程序设计的全部,本章将讨论几类数论问题,并用程序实现它们。

01、实例分析：阿里巴巴的宝藏

问题描述:

阿里巴巴和马尔吉娜来到一条布满黄金的街道。他们想带几块黄金回去，然而这里的城管担心他们拿得太多，于是要求阿里巴巴和马尔吉娜通过做一个游戏决定最后得到的黄金数量。

游戏规则是这样的:

假设道路长度为n米(左端点为0，右端点为n)，同时给出一个数k(下面会提到k的用法)。

设阿里巴巴初始时的黄金数量为A，马尔吉娜初始时的黄金数量为B。阿里巴巴从1出发走向n-1，马尔吉娜从n-1出发走向1，两人的速度均为1m/s。

假设某一时刻(必须为整数)阿里巴巴的位置为x，马尔吉娜的位置为y，若gcd(n,x)=1且gcd(n,y)=1，那么阿里巴巴的黄金数量A会变为A*kxkg，马尔吉娜的黄金数量B会变为B*kykg。当阿里巴巴到达n-1时，游戏结束。

阿里巴巴想知道游戏结束时A+B的值。

答案为对109+7取模。

输入描述:

一行四个整数n,k,A,B。

输出描述:

输出一个整数，表示答案。

样例:

 
示例1:
输入:
4 2 1 1
输出:
32
示例2:
输入:
5 1 1 1
输出:
2

思路如下。

若gcd(n,x)=1，则gcd(n,n-x)=1，同时，若在某个位置得到kx的贡献，那么一定存在一个位置会获得小于或等于k∧n-x的贡献，且两人贡献相同。

将贡献单独写出来:

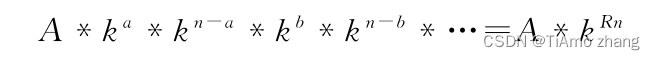
因此需要考虑如何得到R的值，通过题目可知，能产生答案的数一定是与n互质的数，即欧拉函数的值。

由于前n个数的欧拉函数的和为

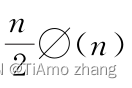
，因此最终答案为

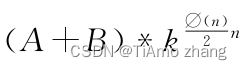
 参考程序:

#include<iostream>
# include< cstdio>
#include<cstdlib>
#include< string>
#include<cstring>
# include< cmath>
#include< ctime>
#include<algorithm>
# include<utility>
# include< stack>
# include< queue>
#include< deque>
#include<vector>
#include< set>
#include<map>
#define PI acos(-1.0)
#define E e-6
#define INF Ox3f3f3f3f
#define N 10001
#define LL long long
onst int MOD=1e9+ 7;
const int dx[]={-1,1,0,0);
const int dy[]={0,0,-1,1};
using namespace std;
int getPhi(int x) { //获取欧拉函数
int res=x;
for(int i=2;i<=sqrt(x+ 0.5);i++){
if(x%i==0){
res=res/i*(i-1);
while(x%i==0)
X/=i;
}
}
if(X>1)
res=res/x * (x-1) ;
return res;
}
LL quickPOw(LL X,LL a){ //快速幂
LL res=1;
while(a){
if(a&1)
res=res*x%MOD;
X=X*X%MOD;
a>>=1;
}
return res;
}
int main(){
int n;
LL a,b,k;
cin>>n>> k>>a>>b;
int phi=getPhi(n);
LL res=quickPow(k,phi/2 *n);
res=res*(a+b)%MOD;
cout<<res<<endl;
return 0;
}

02、实例分析：欧拉函数例题

问题描述:

给定一个数字N，输出N的欧拉函数值。

输入:

输入包含一个正整数N，2≤N≤2000000000。

输出:

输出一个整数，表示N的欧拉函数值。

输入样例:

6
5

输出样例:

2
4

解题思路:

设一个数

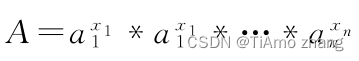
，那么A的欧拉函数

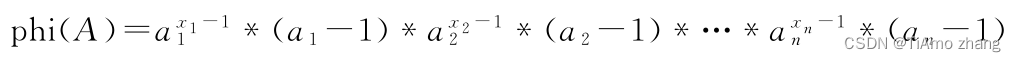
整理公式后得

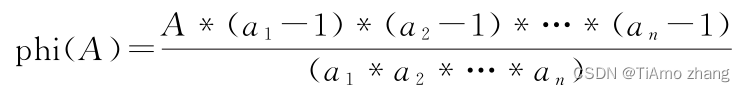
当整理出这个公式的时候，不难发现，从这个公式出发能很容易地用程序实现求phi(A)的操作。

具体做法就是先令temp=A，然后每找到一个A的质因子,就从temp中除掉一个此因子，然后再乘上（此因子-1）。

通过这道题目，我们发现在解一些数学类问题的时候，往往推出的公式能帮我们简化程序。

参考程序:

# include <stdio.h>
# include <stdlib.h>
typedef_int64 inta;
inta phi(inta a) {  //求 a 的欧拉函数值
inta temp=a;
for (inta i=2;i*i<=a;i++)  //寻找 a 的质因子
if (a%i==0){
while (!(a%i)) a/=i;
temp=temp/i*(i-1) ;
}
if (a!=1) temp= temp/a* (a- 1);
return temp;
}
int main(){
inta a;
while (scanf("%I64d",&a) !=EOF)
printf("%I64d\n",phi(a));
return 0;
}