用PyTorch轻松实现二分类:逻辑回归入门
🥦引言
当谈到机器学习和深度学习时,逻辑回归是一个非常重要的算法,它通常用于二分类问题。在这篇博客中,我们将使用PyTorch来实现逻辑回归。PyTorch是一个流行的深度学习框架,它提供了强大的工具来构建和训练神经网络,适用于各种机器学习任务。
在机器学习中已经使用了sklearn库介绍过逻辑回归,这里重点使用pytorch这个深度学习框架
🥦什么是逻辑回归?
我们首先来回顾一下什么是逻辑回归?
逻辑回归是一种用于二分类问题的监督学习算法。它的主要思想是通过一个S形曲线(通常是Sigmoid函数)将输入特征映射到0和1之间的概率值,然后根据这些概率值进行分类决策。在逻辑回归中,我们使用一个线性模型和一个激活函数来实现这个映射。
🥦分类问题
这里以MINIST Dataset手写数字集为例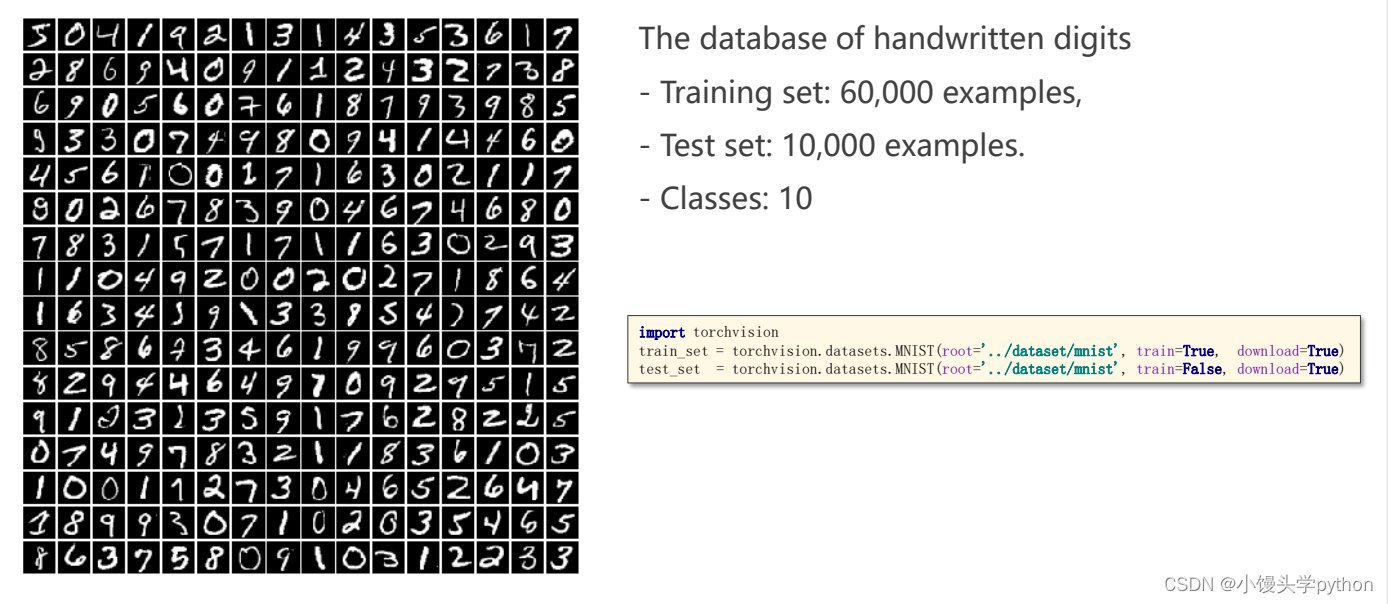
这个数据集中包含了6w个训练集1w个测试集,类别10个
这里我们不再向之前线性回归那样,根据属于判断具体的数值大小;而是根据输入的值判断从0-9每个数字的概率大小记为p(0)、p(1)…而且十个概率值和为1,我们的目标就是根据输入得到这十个分类对于输入的每一个的概率值,哪个大就是我们需要的。
这里介绍一下与torch相关联的库—torchvision
torchvision:
- “torchvision” 是一个PyTorch的附加库,专门用于处理图像和视觉任务。
它包含了一系列用于数据加载、数据增强、计算机视觉任务(如图像分类、目标检测等)的工具和数据集。 - “torchvision” 提供了许多预训练的视觉模型(例如,ResNet、VGG、AlexNet等),可以用于迁移学习或作为基准模型。
此外,它还包括了用于图像预处理、转换和可视化的函数。
上图已经清楚的显示了,这个库包含了一些自带的数据集,但是并不是我们安装完这个库就有了,而且需要进行调用的,类似在线下载,root指定下载的路径,train表示你需要训练集还是测试集,通常情况下就是两个一个训练,一个测试,download就是判断你下没下载,下载了就是摆设,没下载就给你下载了
我们再来看一个数据集(CIFAR-10)
包含了5w训练样本,1w测试样本,10类。调用方式与上一个类似。
接下来我们从一张图更加直观的查看分类和回归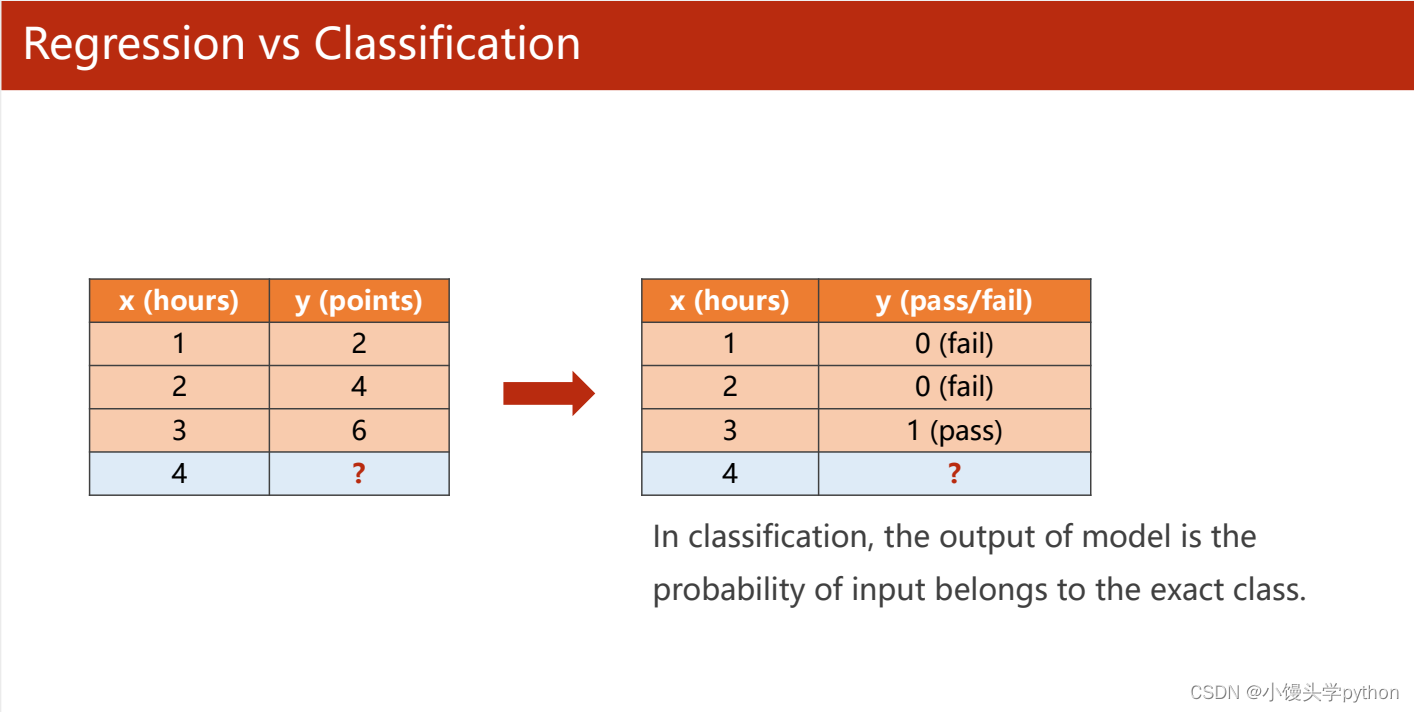
左边的是回归,右边的是分类
过去我们使用回归例如y ^ \hat{y}y^=wx+b∈R,这是属于一个实数的;但是在分类问题,y ^ \hat{y}y^∈[0,1]
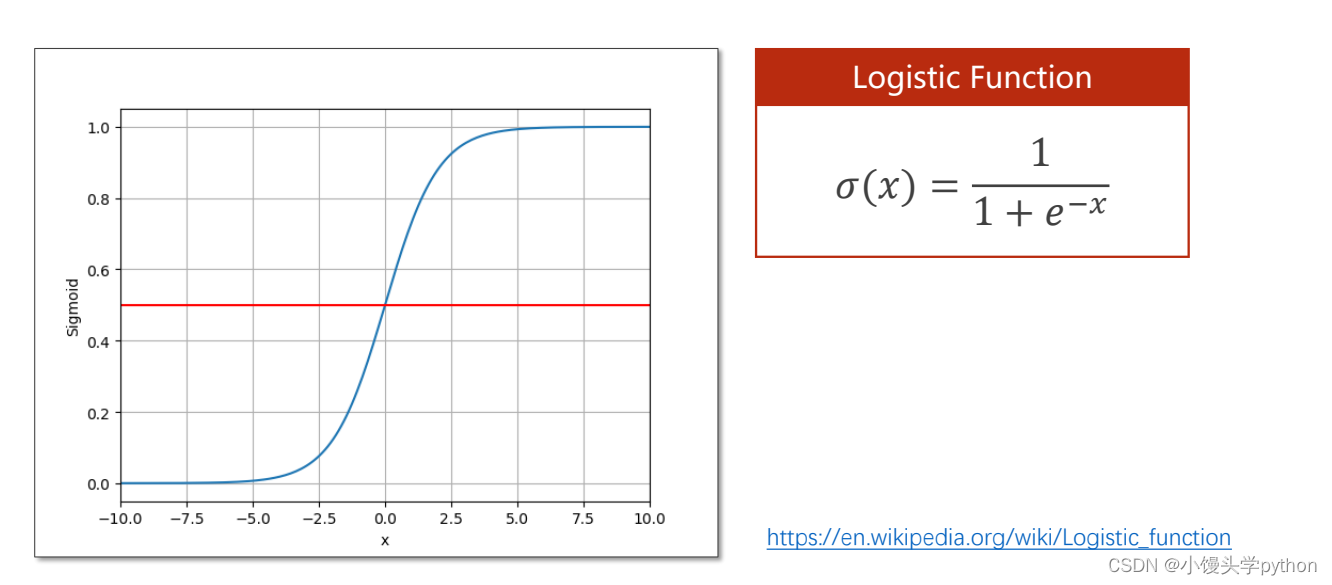
这说明我们需要寻找一个函数,将原本实数的值经过函数的映射转化为[0,1]之间。这里我们引入Logistic函数,使用极限很清楚的得出x趋向于正无穷的时候函数为1,x趋向于负无穷的时候,函数为0,x=0的时候,函数为0.5,当我们计算的时候将y ^ \hat{y}y^带入这样就会出现一个0到1的概率了。
下图展示一些其他的Sigmoid函数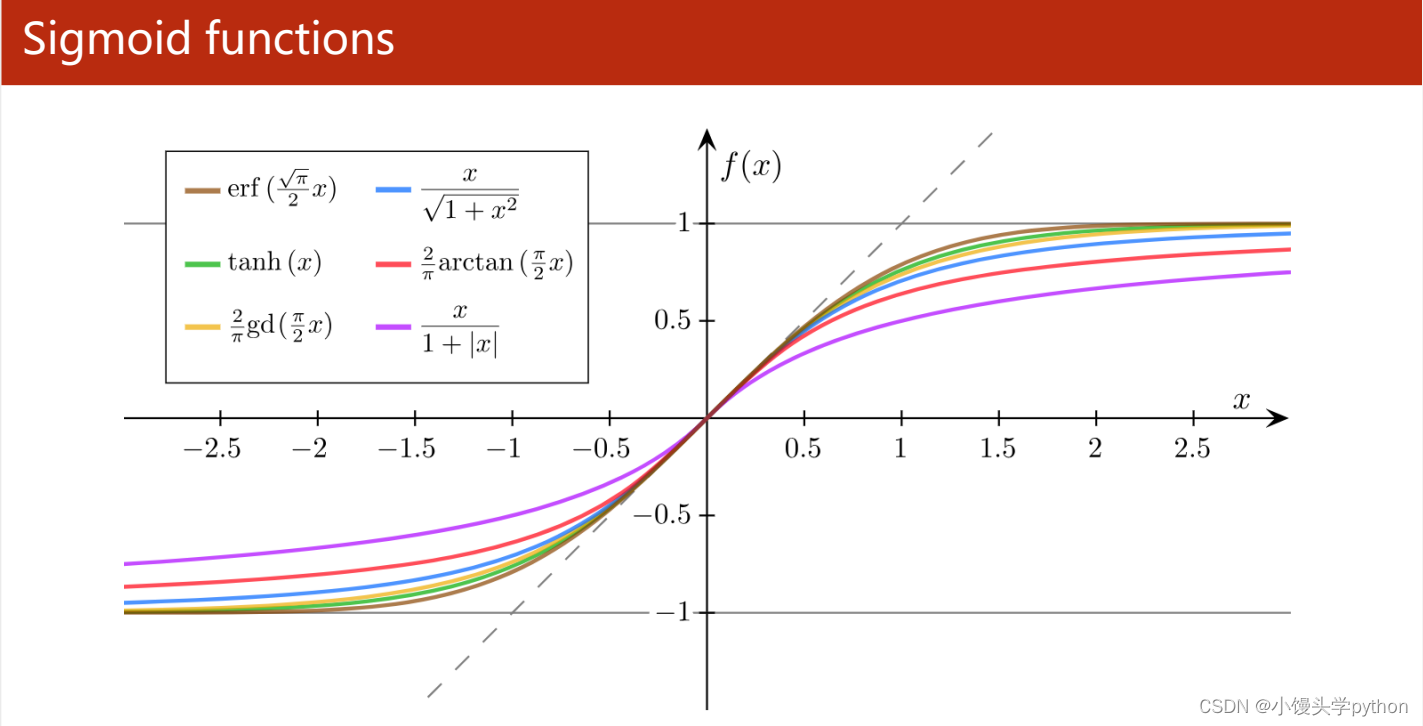
🥦交叉熵
过去我们所使用的损失函数普遍都是MSE,这里引入一个新的损失函数—交叉熵
==交叉熵(Cross-Entropy)==是一种用于衡量两个概率分布之间差异的数学方法,常用于机器学习和深度学习中,特别是在分类问题中。它是一个非常重要的损失函数,用于衡量模型的预测与真实标签之间的差异,从而帮助优化模型参数。
在交叉熵的上下文中,通常有两个概率分布:
真实分布(True Distribution): 这是指问题的实际概率分布,表示样本的真实标签分布。通常用p ( x ) p(x)p(x)表示,其中x xx表示样本或类别。
预测分布(Predicted Distribution): 这是指模型的预测概率分布,表示模型对每个类别的预测概率。通常用q ( x ) q(x)q(x)表示,其中x xx表示样本或类别。
交叉熵的一般定义如下: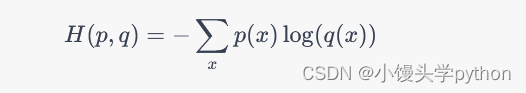 其中,H ( p , q ) H(p, q)H(p,q) 表示真实分布 p pp 和预测分布 q qq 之间的交叉熵。
其中,H ( p , q ) H(p, q)H(p,q) 表示真实分布 p pp 和预测分布 q qq 之间的交叉熵。
交叉熵的主要特点和用途包括:
度量差异性: 交叉熵度量了真实分布和预测分布之间的差异。当两个分布相似时,交叉熵较小;当它们之间的差异增大时,交叉熵增大。
损失函数: 在机器学习中,交叉熵通常用作损失函数,用于衡量模型的预测与真实标签之间的差异。在分类任务中,通常使用交叉熵作为模型的损失函数,帮助模型优化参数以提高分类性能。
反向传播: 交叉熵在训练神经网络时非常有用。通过计算交叉熵的梯度,可以使用反向传播算法来调整神经网络的权重,从而使模型的预测更接近真实标签。
在分类问题中,常见的交叉熵损失函数包括二元交叉熵(Binary Cross-Entropy)和多元交叉熵(Categorical Cross-Entropy)。二元交叉熵用于二分类问题,多元交叉熵用于多类别分类问题。
刘二大人的PPT中也介绍了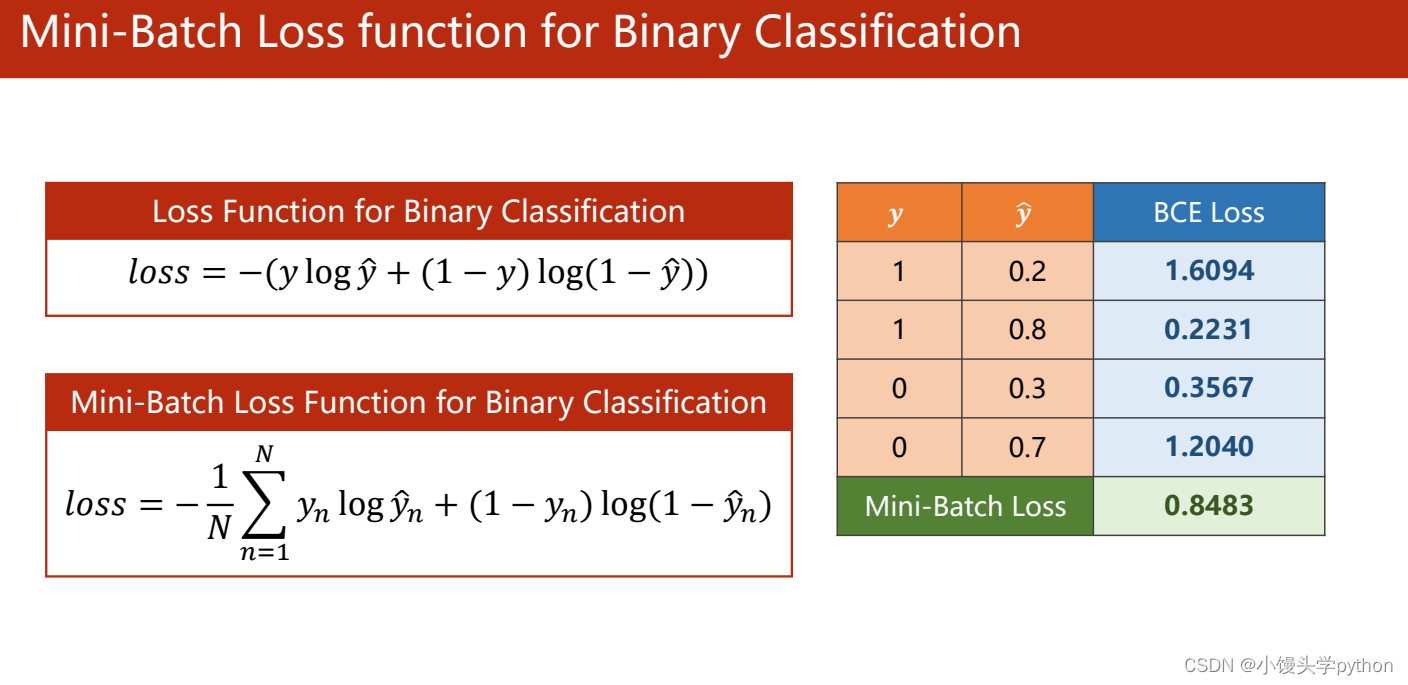
右边的表格中每组y与y ^ \hat{y}y^对应的BCE,BCE越高说明越可能,最后将其求均值
🥦代码实现
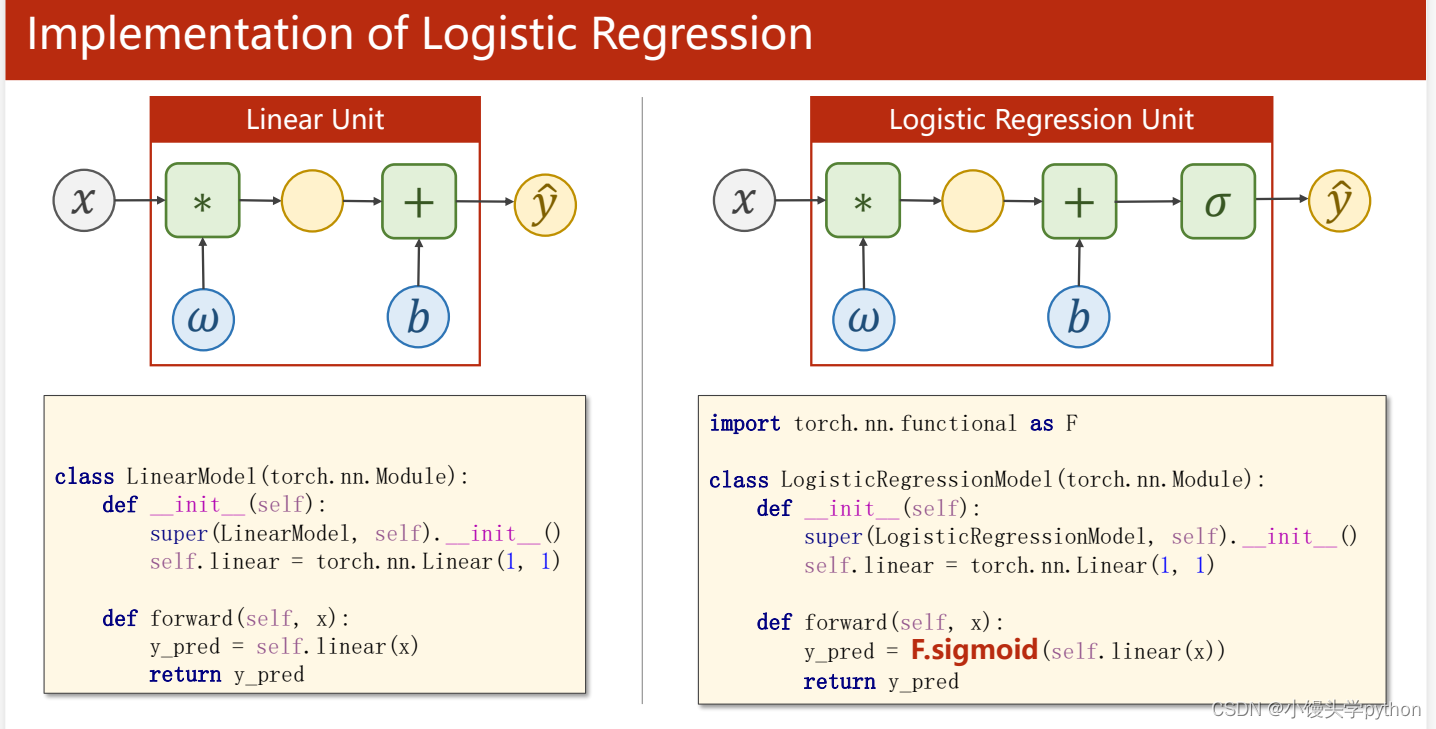
根据上图可知,线性回归和逻辑回归的流程与函数只区别于Sigmoid函数
这里就是BCEloss的调用,里面的参数代表求不求均值
完整代码如下
import torch.nn.functional as F
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[0], [0], [1]])
class LogisticRegressionModel(torch.nn.Module):
def __init__(self):
super(LogisticRegressionModel, self).__init__()
self.linear = torch.nn.Linear(1, 1)
def forward(self, x):
y_pred = F.sigmoid(self.linear(x))
return y_pred
model = LogisticRegressionModel()
criterion = torch.nn.BCELoss(size_average=False)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
for epoch in range(1000):
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
print(epoch, loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
最后绘制一下
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 10, 200)
x_t = torch.Tensor(x).view((200, 1)) # 相当于reshape
y_t = model(x_t)
y = y_t.data.numpy()
plt.plot(x, y)
plt.plot([0, 10], [0.5, 0.5], c='r')
plt.xlabel('Hours')
plt.ylabel('Probability of Pass')
plt.grid()
plt.show()
运行结果如下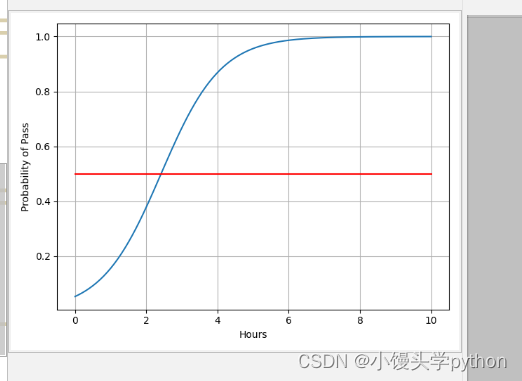
🥦总结
这就是使用PyTorch实现逻辑回归的基本步骤。逻辑回归是一个简单但非常有用的算法,可用于各种分类问题。希望这篇博客能帮助你开始使用PyTorch构建自己的逻辑回归模型。如果你想进一步扩展你的知识,可以尝试在更大的数据集上训练模型或探索其他深度学习算法。祝你好运!

挑战与创造都是很痛苦的,但是很充实。
- 点赞
- 收藏
- 关注作者



评论(0)