逻辑回归与多项式特征：解密分类问题的强大工具

🍋引言

在机器学习领域，逻辑回归是一种常用的分类算法，它可以用于解决诸如垃圾邮件过滤、疾病预测和客户流失分析等各种分类问题。然而，有时候简单的线性逻辑回归模型无法捕捉到数据中的复杂关系。为了更好地处理这些情况，我们可以引入多项式特征，从而提高模型的表现。

🍋逻辑回归简介

逻辑回归是一种广泛应用于二元分类问题的监督学习算法。它通过将输入特征线性组合并通过一个逻辑函数（也称为Sigmoid函数）将结果映射到0和1之间的概率值。这个概率值可以用来进行分类决策，通常当概率值大于0.5时，将样本分类为正类，否则为负类。

逻辑回归的数学表示如下：

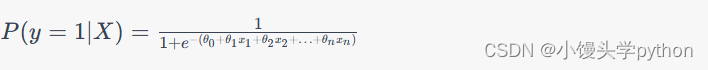
其中，$P(y=1|X)$ 是样本为正类的概率，$X$ 是输入特征向量，$\theta$ 是模型参数。

🍋引入多项式特征

有时候，数据中的关系并不是简单的线性关系。这时，使用线性模型可能无法很好地拟合数据。为了解决这个问题，我们可以引入多项式特征。多项式特征是原始特征的幂次方程，例如，如果原始特征是$x$，那么x 2 x^2x2、x 3 x^3x3等都可以作为多项式特征。

考虑一个简单的例子，假设我们要预测一个学生的考试成绩与其学习时间之间的关系。如果我们只使用学习时间作为特征，那么这个关系可能是非线性的。但是，如果我们引入学习时间的平方作为多项式特征，模型就能更好地拟合数据。

多项式特征的数学表示如下：

将多项式特征引入逻辑回归模型后，模型的表达式将变得更复杂，但它将能够更好地适应非线性数据。

🍋为什么要使用多项式特征？

使用多项式特征的主要原因是增加模型的复杂性，从而更好地拟合非线性关系的数据。这对于许多现实世界的问题非常重要，因为大多数问题的数据都不会完全遵循线性关系。使用多项式特征还可以防止欠拟合，提高模型的准确性。

但是，需要谨慎使用多项式特征，因为它们可能导致过拟合，特别是在高次多项式的情况下。过拟合会使模型在训练数据上表现很好，但在未见过的数据上表现糟糕。因此，在使用多项式特征时，通常需要进行模型选择和超参数调整，以确保模型的泛化能力。

🍋代码演示

首先还是导入numpy和matplotlib库，并假设一组数据

import numpy as np
import matplotlib.pyplot as plt
np.random.seed(666)
X = np.random.normal(0,1,size=(200,2))
y = np.array(X[:,0]**2+X[:,1]**2<1.6,dtype='int')
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

运行结果如下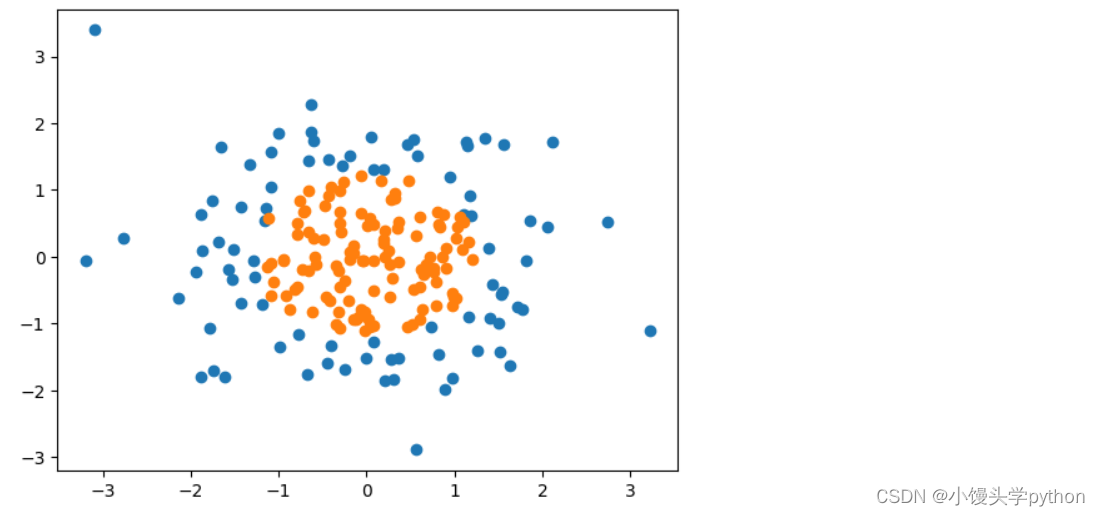

之后我们简单的看一下，在没有进行任何处理的情况下使用逻辑回归拟合后的模型准确率

from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X,y)
log_reg.score(X,y)

不难看出准确率真的差的离谱

在进行之后的学习前，这里引入一个决策边界

def plot_decision_boundary(model,axis):   #  绘制决策边界
    x0,x1 = np.meshgrid(
    np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
    np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1)
    )
    X_new = np.c_[x0.ravel(),x1.ravel()]
    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(["#EF9A9A",'#FFF59D','#90CAF9'])
    plt.contourf(x0,x1,zz,cmap=custom_cmap)

结尾我会进行说明
接下来我们进行绘制

plot_decision_boundary(log_reg,[-4,4,-4,4])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

运行结果如下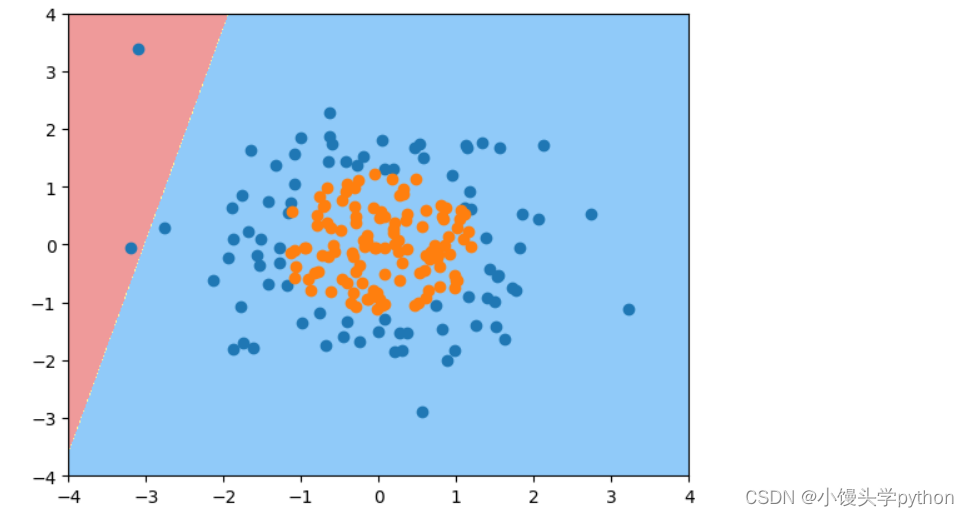

这有助于直观地理解模型如何对数据进行分类，以及决策边界的位置和形状如何影响分类结果

之后我们引入多项式特征，还是创建一个管道，并进行拟合

from sklearn.preprocessing import StandardScaler,PolynomialFeatures
from sklearn.pipeline import Pipeline
def ployRegression(degree):
    return Pipeline([
        ('ploy',PolynomialFeatures(degree)),
        ('std_scaler',StandardScaler()),
        ('log_reg',LogisticRegression())
    ])
log_reg = ployRegression(2)
log_reg.fit(X,y)
log_reg.score(X,y)

运行结果如下

这个准确率看起来不错的羊子~

使用决策边界再看看

plot_decision_boundary(log_reg,[-4,4,-4,4])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

运行结果如下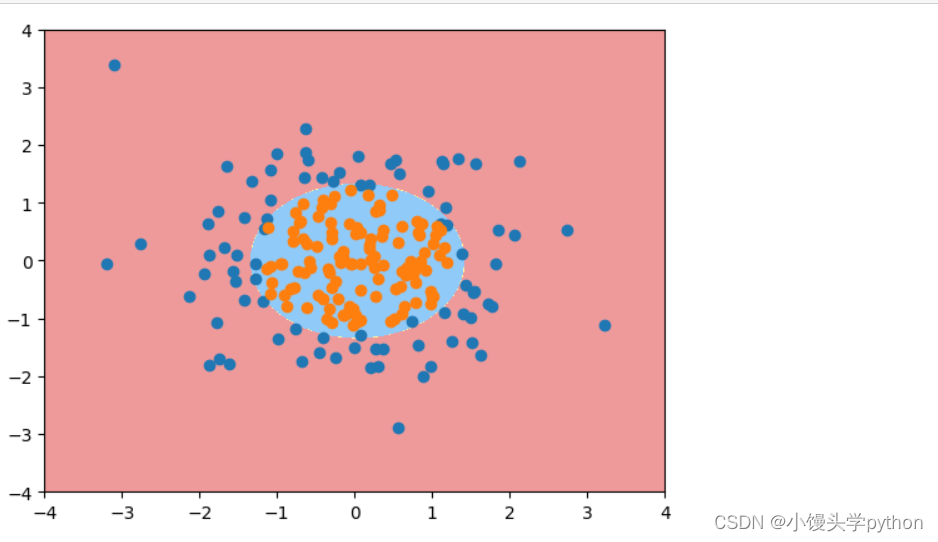

如果将参数degree调大一点，调成20呢

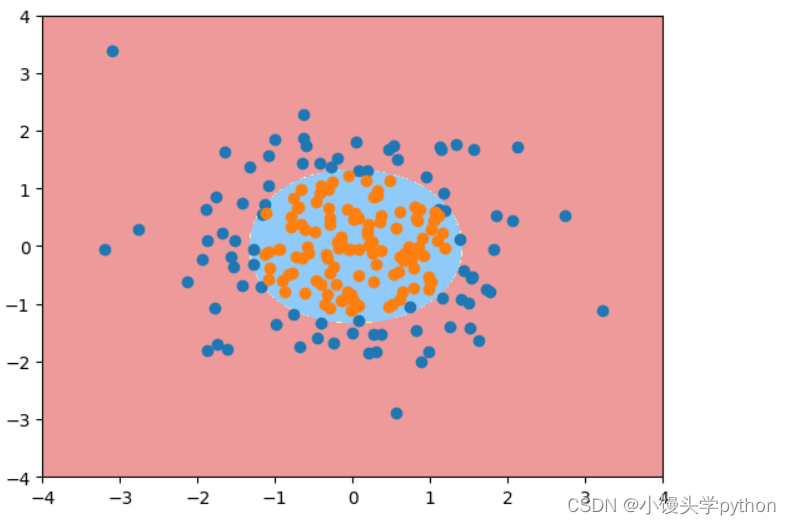
过大就容易过拟合了

接下来我们假设数据换成抛物线的形式，再来看看

np.random.seed(666)
X = np.random.normal(0,1,size=(200,2))
y = np.array(X[:,0]**2+X[:,1]<1.5,dtype='int')

for _ in range(20):
    y[np.random.randint(0,200)] = 1

plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

运行结果如下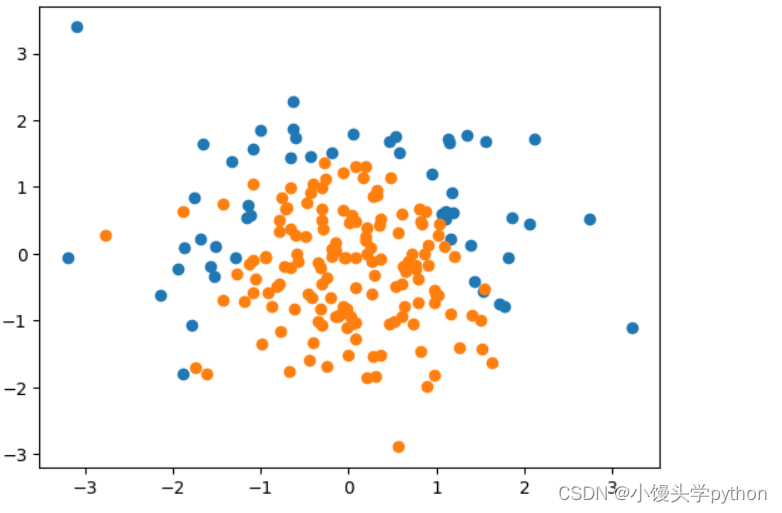

for _ in range(20): y[np.random.randint(0, 200)] = 1：这个循环用于随机地将 y 中的20个标签从0改为1。它通过在0到199之间的随机索引位置上将 y 中的元素设置为1来实现。这个操作相当于将一部分数据点的分类标签更改为1，从而使数据集更具挑战性和复杂性。其实就是添加噪音分子

和之前一样，我们看看对应的决策边界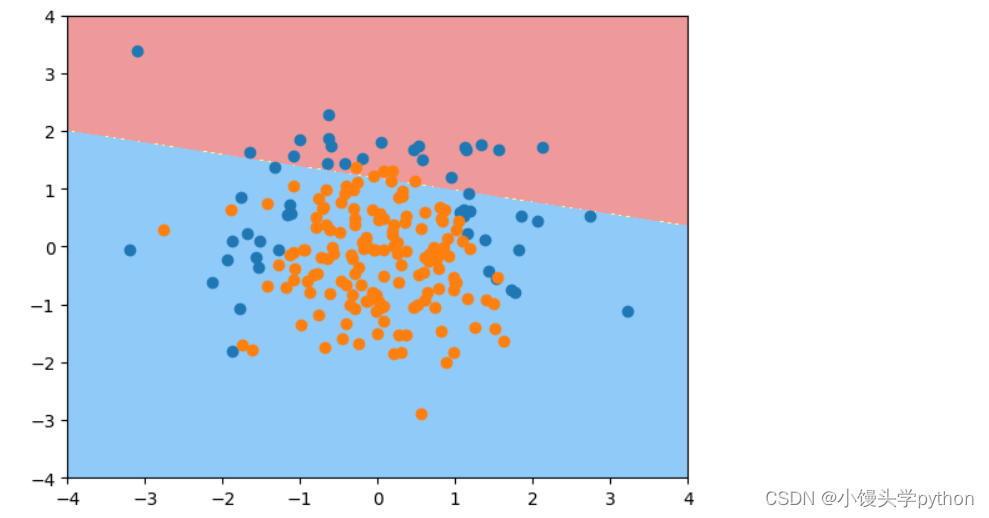

接下来我们采用多项式特征

def polyRegression(degree,C):
    return Pipeline([
        ('poly',PolynomialFeatures(degree)),
        ('std_scaler',StandardScaler()),
        ('log_reg',LogisticRegression(C=C))
    ])

这次我们新引入了一个参数C，代表正则化的强度

log_reg = polyRegression(2,1)
log_reg.fit(X_train,y_train)
print(log_reg.score(X_test,y_test))
plot_decision_boundary(log_reg,[-4,4,-4,4])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

运行结果如下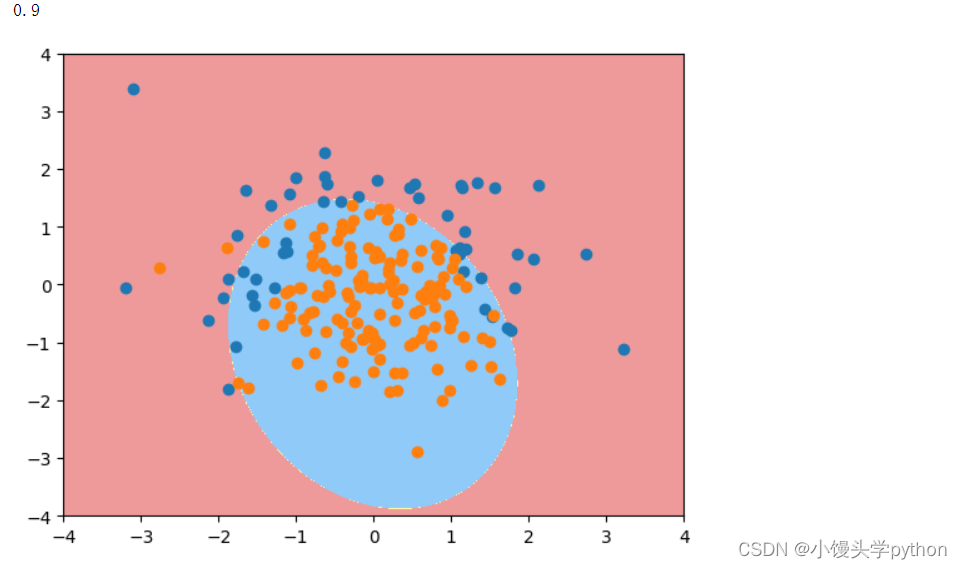

可以将degree调到20再来看看

log_reg = polyRegression(20,1)
log_reg.fit(X_train,y_train)
print(log_reg.score(X_test,y_test))
plot_decision_boundary(log_reg,[-4,4,-4,4])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

运行结果如下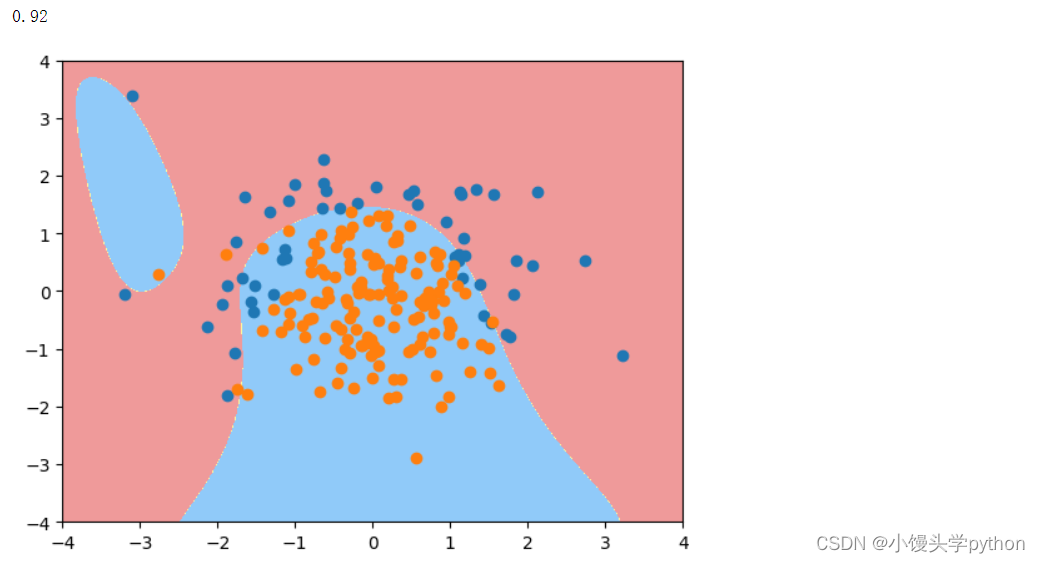

最后我们可以再看看penalty参数

def polyRegression(degree,C,penalty):
    return Pipeline([
        ('poly',PolynomialFeatures(degree)),
        ('std_scaler',StandardScaler()),
        ('log_reg',LogisticRegression(C=C,penalty=penalty,solver='liblinear' if penalty=='l1' else 'lbfgs'))
    ])
log_reg = polyRegression(20,0.1,'l1')
log_reg.fit(X_train,y_train)
print(log_reg.score(X_test,y_test))
plot_decision_boundary(log_reg,[-4,4,-4,4])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

solver：求解器，根据正则化类型不同而选择不同的求解方法。如果是 L1 正则化，使用 ‘liblinear’ 求解器，否则使用 ‘lbfgs’ 求解器。

这个管道的目的与前面的函数一样，是将多项式特征转换、特征标准化和逻辑回归组合在一起，形成一个整体的机器学习模型。不同之处在于，这次可以通过参数 penalty 来指定正则化类型，并根据不同的类型选择不同的求解方法。

运行结果如下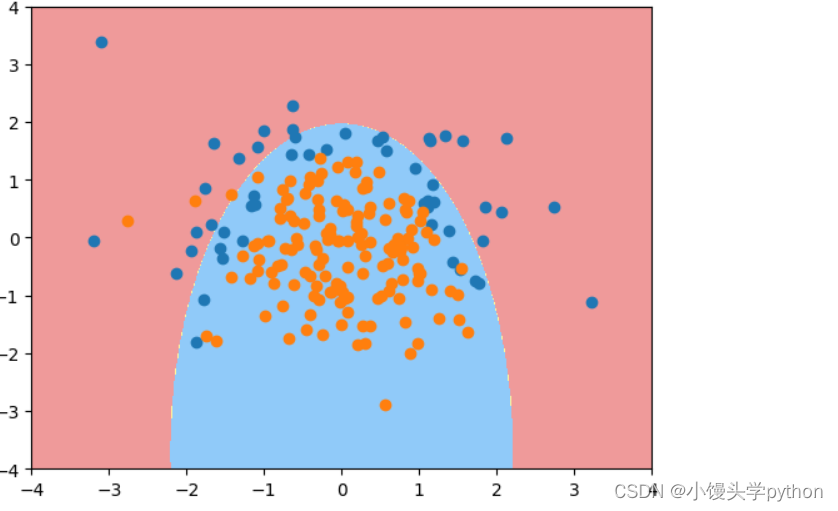

最后总结一下：使用这个函数时，你需要提供 degree、C 和 penalty 参数的值来配置管道中的多项式特征的阶数、逻辑回归的正则化强度和正则化类型。然后，你可以使用这个管道来训练和测试机器学习模型，具体配置取决于你传递给函数的参数。

🍋决策边界

在机器学习和统计建模中，决策边界（Decision Boundary）是一个重要的概念，它表示模型将数据分为不同类别或类别的界限。决策边界可以是一个超平面、曲线或者更复杂的形状，具体取决于所使用的分类算法和数据的特性。

决策边界的主要作用是将特征空间分割成不同的区域，每个区域对应于模型预测的不同类别或类别的决策。通常，数据点位于决策边界的一侧被分为一个类别，而位于另一侧的数据点被分为另一个类别。决策边界的位置和形状直接受到模型的参数和算法的影响。

以下是一些示例：

• 线性决策边界：在线性分类问题中，决策边界通常是一个直线（在二维空间中）或一个超平面（在高维空间中），将数据分为两个类别。例如，线性支持向量机（Linear SVM）通常使用线性决策边界。

• 非线性决策边界：在某些情况下，数据可能无法用简单的直线或超平面分隔。此时，需要使用非线性决策边界，如多项式回归、核方法等。这些方法可以捕捉到数据中的非线性关系。

• 复杂决策边界：在某些复杂问题中，决策边界可能具有复杂的形状，如曲线、多边形等。这通常出现在深度学习和复杂的神经网络模型中，这些模型可以学习高度复杂的特征边界。

挑战与创造都是很痛苦的，但是很充实。