2023-10-18：用go语言，给定一个数组arr，长度为n，表示有0~n-1号设备，

arr[i]表示i号设备的型号，型号的种类从0~k-1，一共k种型号，

给定一个k*k的矩阵map，来表示型号之间的兼容情况，

map[a][b] == 1，表示a型号兼容b型号，

map[a][b] == 0，表示a型号不兼容b型号，

兼容关系是有向图，也就是a型号兼容b型号，不代表b型号同时兼容a型号，

如果i设备的型号兼容j设备的型号，那么可以从i设备修建一条去往j设备的线路，

修建线路的代价是i设备到j设备的距离：|i-j|，

你的目标是从0号设备到达n-1号设备，并不一定每个设备都联通，只需要到达即可。

返回最小的修建代价，如果就是无法到达返回-1。

1 <= n <= 1000，

1 <= k <= 50。

来自招商银行。

来自左程云。

答案2023-10-18：

大体步骤:

1.创建一个二维切片 own，长度为 k，用于记录每个型号的设备编号。

2.创建一个二维切片 nexts，长度为 k，用于记录每个型号兼容的下一个型号。

3.遍历数组 arr，将每个设备的编号添加到对应型号的 own 中。

4.遍历兼容矩阵 m，将每个型号兼容的下一个型号添加到对应型号的 nexts 中。

5.创建一个二叉堆 heap，并定义排序函数，按照修建代价升序排列。

6.将起始设备 (0, 0) 添加到堆中，表示从 0 号设备开始，修建代价为 0。

7.创建一个长度为 n 的布尔型切片 visited，用于标记设备是否被访问过。

8.当堆不为空时，进行以下操作：

• 弹出堆顶元素 t，表示当前位置和当前的修建代价。

• 获取当前位置 cur 的设备编号和修建代价。

• 如果当前位置为目标位置 n-1，则返回当前的修建代价。

• 将当前位置标记为已访问。

9.获取当前设备的型号 model。

10.遍历下一个兼容的型号 nextModel，以及拥有下一个型号 nextModel 的设备位置 nextPosition：

 - 如果设备位置未被访问过，则将 `(nextPosition, cost + abs(nextPosition, position))` 添加到堆中。

11.如果无法到达目标位置，返回 -1。

12.在 main 函数中调用 minCost 函数，并输出结果。

总的时间复杂度为 $O(nk^2logn)$，其中 n 是设备数量，k 是型号数量。遍历拥有型号的设备位置的过程复杂度为 O(n)，堆操作的复杂度为 O(logn)，遍历所有可能的型号和设备位置的复杂度为 $O(k^2$)，所以总的时间复杂度为 $O(nk^2logn)$。

总的额外空间复杂度为 O(n)，其中 n 是设备数量。需要额外的空间来存储 own、nexts、visited 和堆 heap，它们的空间复杂度都为 O(n)。

go完整代码如下：

package main

import (
	"fmt"

	"github.com/emirpasic/gods/trees/binaryheap"
)

func minCost(arr []int, m [][]int, n int, k int) int {
	// 0 : {4,7,13,26}
	// 1 : {5,45,3,17}
	own := make([][]int, k)
	nexts := make([][]int, k)
	for i := 0; i < k; i++ {
		own[i] = []int{}
		nexts[i] = []int{}
	}

	for i := 0; i < n; i++ {
		own[arr[i]] = append(own[arr[i]], i)
	}

	for i := 0; i < k; i++ {
		for j := 0; j < k; j++ {
			if m[i][j] == 1 {
				nexts[i] = append(nexts[i], j)
			}
		}
	}

	heap := binaryheap.NewWith(func(a, b interface{}) int {
		return a.([]int)[1] - b.([]int)[1]
	})
	heap.Push([]int{0, 0})

	visited := make([]bool, n)

	for heap.Size() > 0 {
		t, _ := heap.Pop()
		cur := t.([]int)
		position := cur[0]
		cost := cur[1]

		if !visited[position] {
			visited[position] = true

			if position == n-1 {
				return cost
			}

			model := arr[position]

			for _, nextModel := range nexts[model] {
				for _, nextPosition := range own[nextModel] {
					if !visited[nextPosition] {
						heap.Push([]int{nextPosition, cost + abs(nextPosition, position)})
					}
				}
			}
		}
	}

	return -1
}

func abs(a, b int) int {
	if a-b < 0 {
		return b - a
	}
	return a - b
}

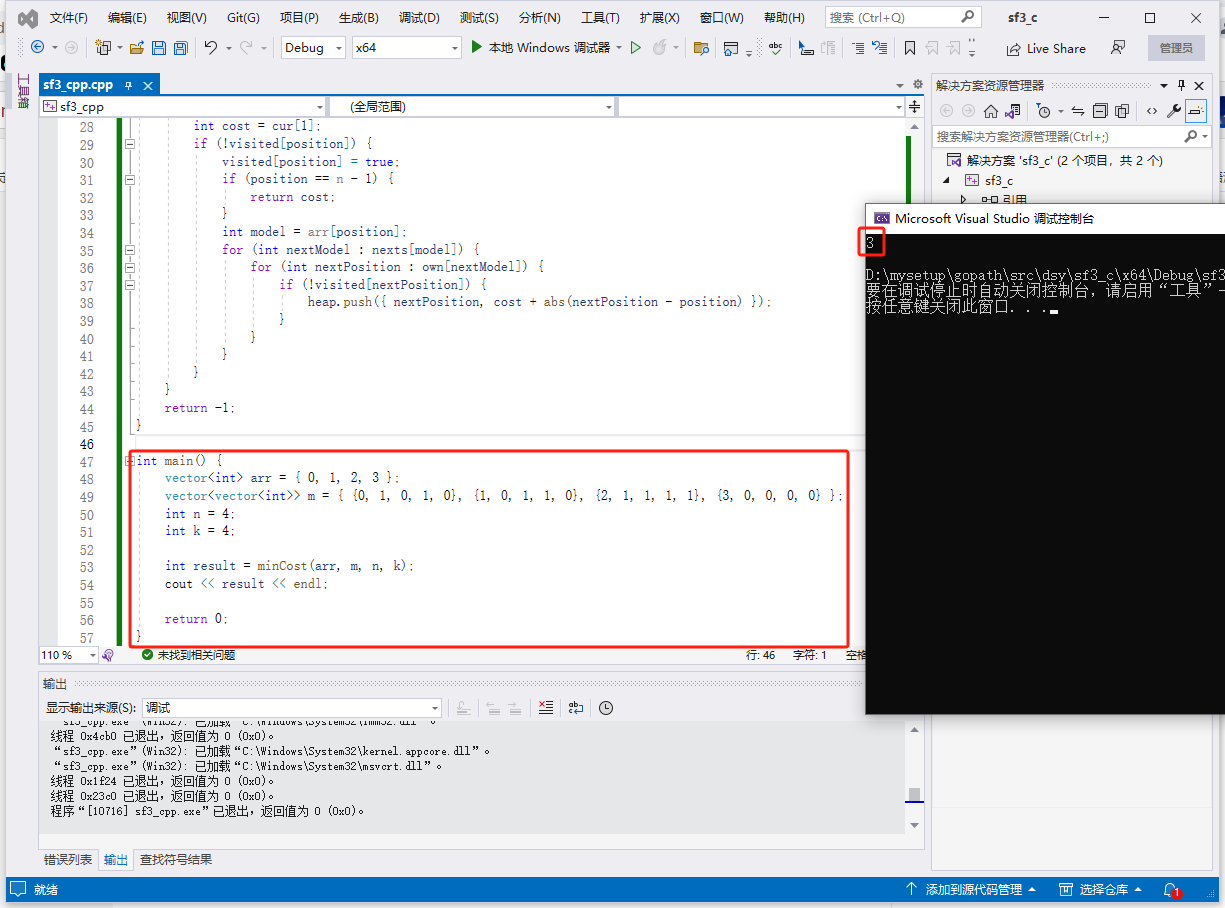
func main() {
	arr := []int{0, 1, 2, 3}
	m := [][]int{{0, 1, 0, 1, 0}, {1, 0, 1, 1, 0}, {2, 1, 1, 1, 1}, {3, 0, 0, 0, 0}}
	n := 4
	k := 4
	result := minCost(arr, m, n, k)
	fmt.Println(result)
}

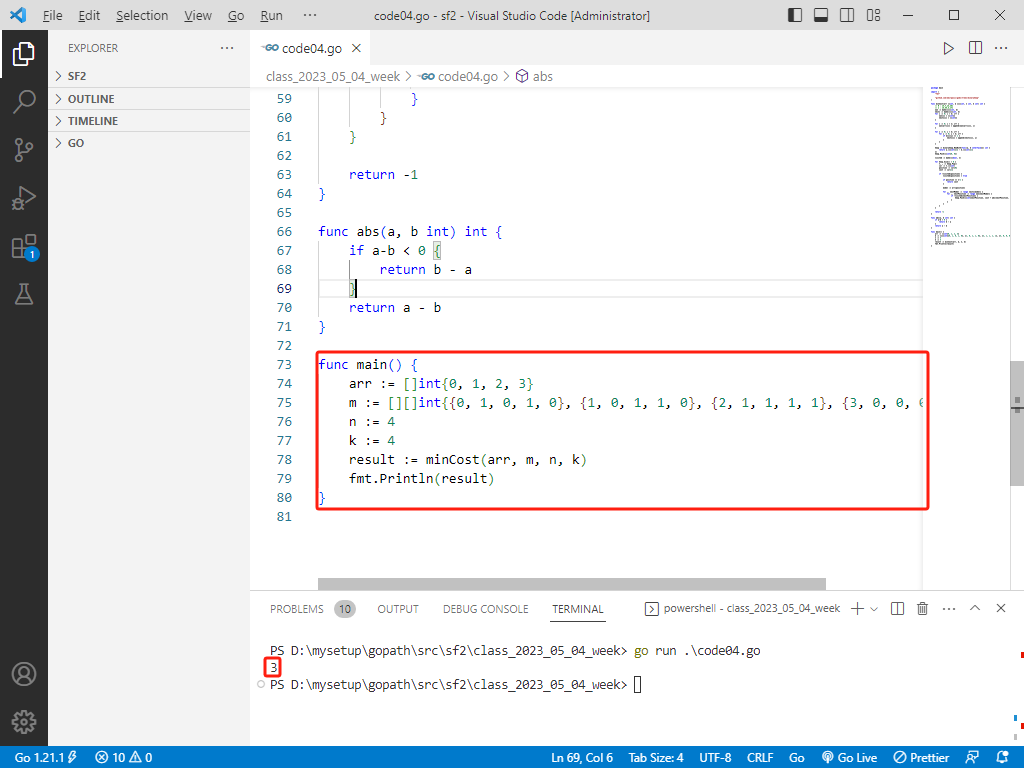
rust完整代码如下：

use std::cmp::Reverse;
use std::collections::BinaryHeap;

fn min_cost(arr: &[i32], map: &[Vec<i32>], n: usize, k: usize) -> i32 {
    let mut own: Vec<Vec<i32>> = vec![Vec::new(); k];
    let mut nexts: Vec<Vec<i32>> = vec![Vec::new(); k];

    for (i, &value) in arr.iter().enumerate() {
        own[value as usize].push(i as i32);
    }

    for (i, row) in map.iter().enumerate() {
        for (j, &value) in row.iter().enumerate() {
            if value == 1 {
                nexts[i as usize].push(j as i32);
            }
        }
    }

    let mut heap: BinaryHeap<(i32, i32)> = BinaryHeap::new();
    heap.push((0, 0));
    let mut visited: Vec<bool> = vec![false; n];

    while let Some((position, cost)) = heap.pop() {
        let position = position as usize;
        let cost = cost;

        if !visited[position] {
            visited[position] = true;

            if position == n - 1 {
                return cost;
            }

            let model = arr[position] as usize;

            for &next_model in &nexts[model] {
                for &next_position in &own[next_model as usize] {
                    if !visited[next_position as usize] {
                        heap.push((
                            next_position,
                            cost + (next_position - position as i32).abs(),
                        ));
                    }
                }
            }
        }
    }

    -1
}

fn main() {
    let arr = [0, 1, 2, 3];
    let m = [
        vec![0, 1, 0, 1, 0],
        vec![1, 0, 1, 1, 0],
        vec![2, 1, 1, 1, 1],
        vec![3, 0, 0, 0, 0],
    ];
    let n = 4;
    let k = 4;

    let result = min_cost(&arr, &m, n, k);
    println!("Minimum Cost: {}", result);
}

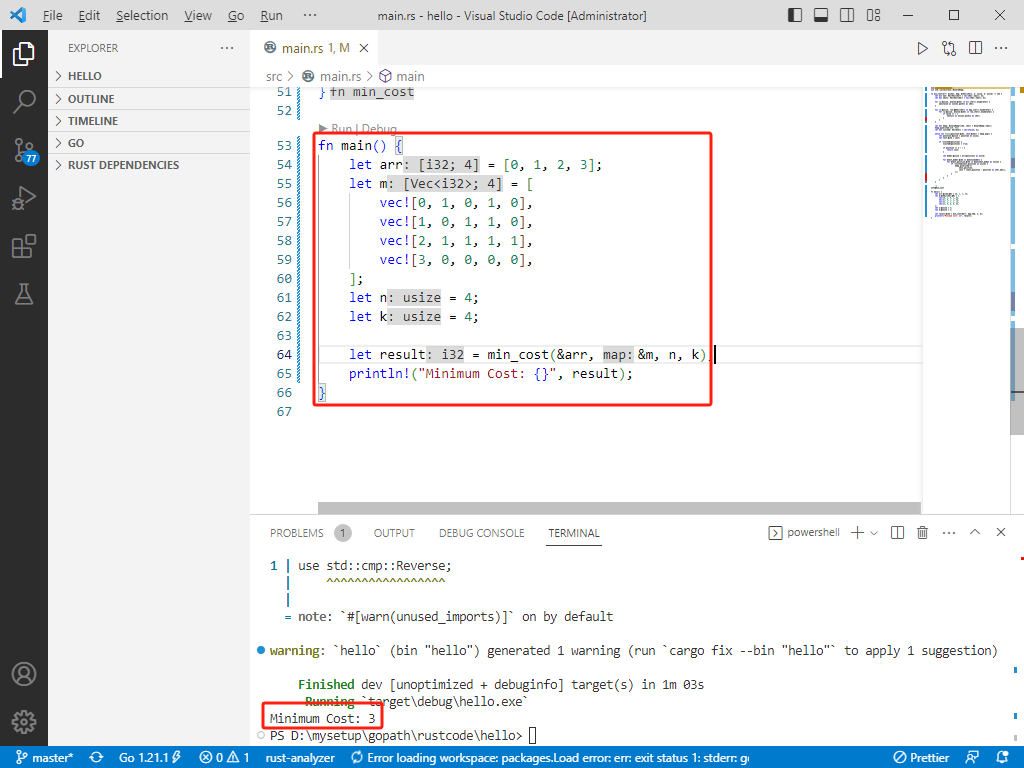
c++完整代码如下：

#include <iostream>
#include <queue>
#include <vector>
#include <cmath>

using namespace std;

int minCost(vector<int>& arr, vector<vector<int>>& map, int n, int k) {
    vector<vector<int>> own(k);
    vector<vector<int>> nexts(k);
    for (int i = 0; i < n; i++) {
        own[arr[i]].push_back(i);
    }
    for (int i = 0; i < k; i++) {
        for (int j = 0; j < k; j++) {
            if (map[i][j] == 1) {
                nexts[i].push_back(j);
            }
        }
    }
    priority_queue<vector<int>, vector<vector<int>>, greater<vector<int>>> heap;
    heap.push({ 0, 0 });
    vector<bool> visited(n, false);
    while (!heap.empty()) {
        vector<int> cur = heap.top();
        heap.pop();
        int position = cur[0];
        int cost = cur[1];
        if (!visited[position]) {
            visited[position] = true;
            if (position == n - 1) {
                return cost;
            }
            int model = arr[position];
            for (int nextModel : nexts[model]) {
                for (int nextPosition : own[nextModel]) {
                    if (!visited[nextPosition]) {
                        heap.push({ nextPosition, cost + abs(nextPosition - position) });
                    }
                }
            }
        }
    }
    return -1;
}

int main() {
    vector<int> arr = { 0, 1, 2, 3 };
    vector<vector<int>> m = { {0, 1, 0, 1, 0}, {1, 0, 1, 1, 0}, {2, 1, 1, 1, 1}, {3, 0, 0, 0, 0} };
    int n = 4;
    int k = 4;

    int result = minCost(arr, m, n, k);
    cout << result << endl;

    return 0;
}