《深入浅出强化学习：原理入门》课后习题答案整理

1 绪论

2 马尔科夫决策过程

2.4 习题

1. Q:马尔科夫过程与马尔科夫决策过程的区别。

A: 马尔科夫过程的定义：马尔科夫过程是一个二元组(S,P),且满足：S是有限状态集合，P是状态转移概率。状态转移概率矩阵为：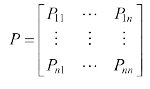

下面我们以一个例子来进行阐述。

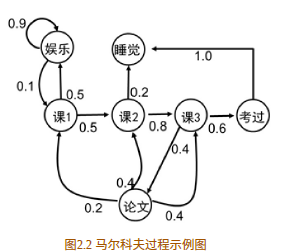
如图2.2所示为一个学生的7种状态{娱乐，课程1，课程2，课程3，考过，睡觉，论文}，每种状态之间的转换概率如图所示。则该生从课程1开始一天可能的状态序列为:

课1-课2-课3-考过-睡觉

课1-课2-睡觉

以上状态序列称为马尔科夫链。当给定状态转移概率时，从某个状态出发存在多条马尔科夫链。对于游戏或者机器人，马尔科夫过程不足以描述其特点，因为不管是游戏还是机器人，他们都是通过动作与环境进行交互，并从环境中获得奖励，而马尔科夫过程中不存在动作和奖励。将动作（策略）和回报考虑在内的马尔科夫过程称为马尔科夫决策过程。

马尔科夫决策过程

马尔科夫决策过程是由元组(S,A,P,R,γ)描述，其中：

S为有限的状态集

A为有限的动作集

P为状态转移概率

R为回报函数

γ为折扣因子，用来计算累积回报。

注意，跟马尔科夫过程不同的是，马尔科夫决策过程的状态转移概率是包含动作的，即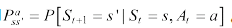

举个例子如图2.3所示。

图2.3为马尔科夫决策过程的示例图，图2.3与图2.2对应。在图2.3中，学生有5个状态，状态集为S={s1,s2,s3,s4,s5},动作集为A={玩，退出，学习，发表，睡觉}，在图2.3中立即回报用R标记。

强化学习的目标是给定一个马尔科夫决策过程，寻找最优策略。所谓策略是指状态到动作的映射。

2. Q:随机策略的理解

A:在强化学习算法中，随机策略得到⼴泛应⽤，因为随机策略耦合了探索。后⾯要介绍的很多强化学习算
法的策略都采⽤随机策略，所以，很有必要理解什么是随机策略。随机策略常⽤符号π表⽰，它是指给定状态s时动作集上的⼀个分布。要理解分布⾸先要理解随机变量[2] 。
（1）随机变量。
随机变量是指可以随机地取不同值的变量，常⽤⼩写字⺟表⽰。在MDP中随机变量指的是当前的动作，⽤字⺟ 表⽰。在图2.3的例⼦中，随机变量 可取的值为“玩”、“退出”、“学习”、“发表”和“睡觉”。随机变量可以是离散的也可以是⾮离散的，在该例⼦中随机变量是离散的。有了随机变量，我们就可以描述概率分布了。
（2）概率分布。
概率分布⽤来描述随机变量在每个可能取到的值处的可能性⼤⼩。离散型随机变量的概率分布常⽤概率质量函数来描述，即随机变量在离散点处的概率。连续型随机变量的概率分布则⽤概率密度函数来描述。在图 2.3的例⼦中，指定⼀个策略π就是指定取每个动作的概率。
（3）条件概率。
策略π（a|s）是条件概率。条件概率是指在其他事件发⽣时，我们所关⼼的事件所发⽣的概率。在我们的例⼦中π（a|s）是指在当前状态s处，采取某个动作a的概率。当给定随机变量后，状态s处的累积回报G(s)也是随机变量，⽽且其分布由随机策略π决定。状态值函数定义为该累积回报的期望。

最常⽤的概率分布也就是最常⽤的随机策略。

（1）贪婪策略

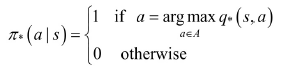
贪婪策略是⼀个确定性策略，即只有在使得动作值函数q* （s，a）最⼤的动作处取概率1，选其他动作的概率为0。

（2）ε-greedy策略。

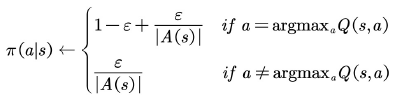
ε-greedy平衡了利⽤（exploitation）和探索（exploration），其中选取动作值函数最⼤的部分为利⽤，其他⾮最优动
作仍有概率为探索部分。

（3）⾼斯策略。
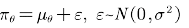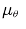⼀般⾼斯策略可以写成 。其中为确定性部分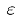， 为零均值的⾼斯随机噪声。⾼斯策略也平衡了利⽤和探索，其中利⽤由确定性部分完成，探索由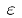完成。⾼斯策略在连续系统的强化学习中应⽤⼴泛。

（4）玻尔兹曼分布。
对于动作空间是是离散的或者动作空间并不⼤的情况，可采⽤玻尔兹曼分布作为随机策略，即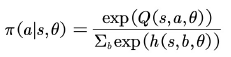

其中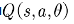，为动作值函数。该策略的含义是，动作值函数⼤的动作被选中的概率⼤，动作值函数⼩的动作被选中的概率⼩。

3. Q:安装gym并测试其中的CartPole实例

A:

4. 基于gym构建如下迷宫世界：

3 基于模型的动态规划算法

3.5 习题

1. 什么是策略迭代算法，什么是值迭代算法，两者的区别和联系是什么。

策略迭代算法：

策略迭代泛包括策略评估和策略改善两个步骤。在策略评估中，给定策略，通过数值迭代算法不断计算该策略下每个状态的值函数，利用该数值迭代算法不断计算该策略下每个状态的值函数，利用该值函数和贪婪策略得到新的策略。如此循环下去，最终得到最优策略。这是一个策略收敛的过程。

值迭代算法：

**基于策略迭代的方法是交替进行策略评估和策略改善。其中策略评估中需要迭代多次，以保证当前策略评估收敛。值迭代的方法则是在策略评估步只迭代一次。**其伪代码和Python代码实现如图3.21所示。

值迭代需要三重循环，第一重大循环用来保证值函数收敛，第二重中间的循环用来遍历整个状态空间，对应着一次策略评估，第三重最里面的循环则是遍历动作空间，用来选最优动作。

2. 高斯赛德尔迭代算法和雅克比迭代算法的区别是什么。

**当求得新的分量之后，⻢上⽤来计算的迭代算法称为⾼斯-赛德尔迭代法。**对于线性⽅程组，对应于雅克⽐迭代过程（3.21）的⾼斯-赛德尔迭代过程为：

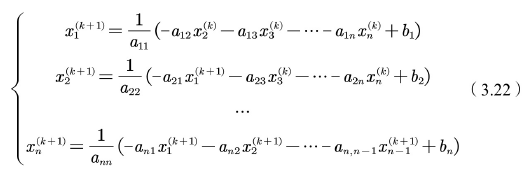
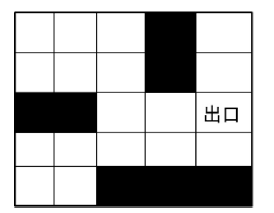
3. 利用动态规划的方法求解如下迷宫问题：

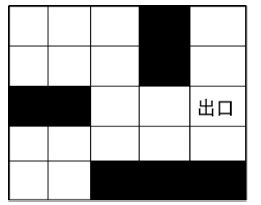
4. 基于HJB方程分别用数值法和DDP的方法分别求解如下带有非完整约束使得机器人路径最优的规划问题：

4 基于蒙特卡罗的强化学习方法

4.4 习题

1. 蒙特卡罗方法可以解决哪些强化学习问题

在没有模型时，我们可以采⽤蒙特卡罗的⽅法计算该期望，即利⽤随机样本估计期望。蒙特卡罗⽅法是利⽤经验平均代替随机变量的期望。由于智能体与环境交互的模型是未知的，蒙特卡罗⽅法是利⽤经验平均来估计值函数，⽽能否得到正确的值函数，则取决于经验——因此，如何获得充⾜的经验是⽆模型强化学习的核⼼所在。

2. 什么是同策略(on-policy),什么是异策略(off-policy),两者的优缺点各是什么。

根据探索策略（⾏动策略）和评估的策略是否为同⼀个策略，蒙特卡罗⽅法⼜分为on-policy和off-policy两种⽅法。
若⾏动策略和评估及改善的策略是同⼀个策略，我们称为on-policy，可翻译为同策略。
若⾏动策略和评估及改善的策略是不同的策略，我们称为off-policy，可翻译为异策略。

异策略可以保证充分的探索性。例如⽤来评估和改善的策略 是贪婪策略，⽤于产⽣数据的探索性策略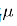为探索性策略，如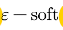策略。
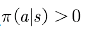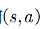⽤于异策略的⽬标策略π和⾏动策略μ并⾮任意选择的，⽽是必须满⾜⼀定的条件。这个条件是覆盖性条件，即⾏动策略μ产⽣的⾏为覆盖或包含⽬标策略π产⽣的⾏为。利⽤式⼦表⽰：满⾜ 的任何均满⾜。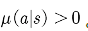

3. 利用蒙特卡罗方法求解下列迷宫问题：

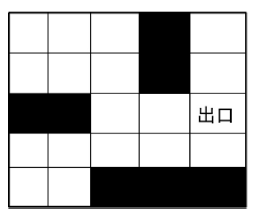
4. 手动编写正态分布的随机样本生成方法

5 基于时间差分的强化学习方法

5.3 习题

1.时间差分方法与蒙特卡罗方法、动态规划方法的区别和联系

第4章我们已经阐述了⽆模型强化学习最基本的⽅法蒙特卡罗⽅法。本章我们阐述另外⼀个⽆模型的⽅法：时间差分⽅法。
时间差分（Temporal-Difference，简称TD）⽅法（如图5.1所⽰）是另⼀种⽆模型强化学习⽅法，也是强化学习理论中最核⼼的内容。与动态规划的⽅法和蒙特卡罗的⽅法相⽐，时间差分⽅法的主要不同在于值函数的估计。

相⽐于动态规划的⽅法，蒙特卡罗的⽅法需要等到每次试验结束，所以学习速度慢，学习效率不⾼。通过对两者的⽐较，我们很⾃然地会想到：能不能借鉴动态规划中bootstrapping的⽅法，在试验未结束时就估计当前的值函数呢？

答案是肯定的，这是时间差分⽅法的精髓。时间差分⽅法结合了蒙特卡罗的采样⽅法（即做试验）和动态规划⽅法的bootstrapping（利⽤后继状态的值函数估计当前值函数），它的计算过程如图5.4所⽰。

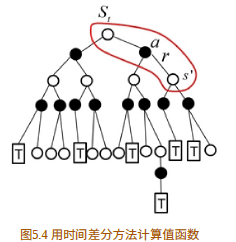
2.如何理解TD(λ)算法的前向视角和后向视角。

如图5.9所⽰为TD(λ)⽅法的前向视⾓解释。假设⼀个⼈坐在状态流上拿着望远镜看前⽅，前⽅是将来的状态。估计当前状态的值函数时，从TD(λ)的定义中可以看到，它需要⽤将来时刻的值函数。也就是说，TD(λ)前向观点通过观看将来状态的值函数来估计当前的值函数。

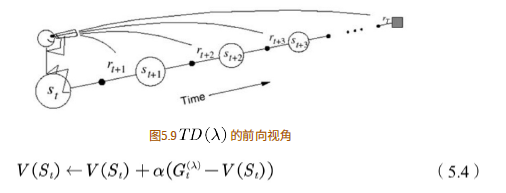
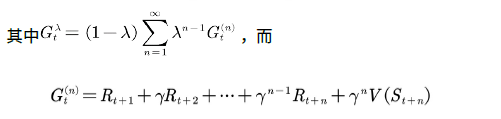
利⽤TD(λ)的前向观点估计值函数时，TD(λ)的计算⽤到了将来时刻的值函数，因此需要整个试验结束后才能计算，这和蒙特卡罗⽅法相似。是否有某种更新⽅法不需要等到试验结束就可以更新当前状态的值函数？

有！这种增量式的更新⽅法需要利⽤TD(λ)的后向观点。

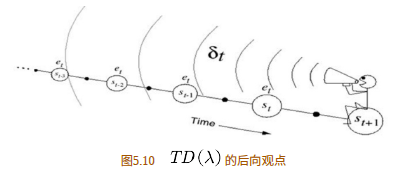
如图 5.10 所⽰为TD(λ)后向观点⽰意图。⼈骑坐在状态流上，⼿⾥拿着话筒，⾯朝已经经历过的状态流，获得当前回报并利⽤下⼀个状态的值函数得到TD偏差后，此⼈会向已经经历过的状态喊话，告诉这些状态处的值函数需要利⽤当前时刻的 TD偏差更新。此时过往的每个状态值函数更新的⼤⼩应该与距离当前状态的步数有关。假设当前状态为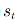，TD偏差为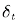，那么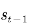处的值函数更新应该乘以⼀个衰减因⼦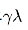，状态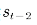处的值函数更新应该乘以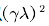，以此类推。

3. 利用Sarsa和Qlearning方法解决下列迷宫问题，并比较它们的差别。

4.修改Qlearning中的探索策略，如使用玻尔兹曼探索，解决上述迷宫问题，并试着比较两者的优劣。

6 基于值函数逼近的强化学习方法

6.4 习题

1. 为什么要引入值函数逼近，他可以解决哪些问题。

前⾯已经介绍了强化学习的基本⽅法：基于动态规划的⽅法，基于蒙特卡罗的⽅法和基于时间差分的⽅法。这些⽅法有⼀个基本的前提条件：状态空间和动作空间是离散的，⽽且状态空间和动作空间不能太⼤。

这些强化学习⽅法的基本步骤是先评估值函数，再利⽤值函数改善当前的策略。其中值函数的评估是关键。
对于模型已知的系统，可以利⽤动态规划的⽅法得到值函数；对于模型未知的系统，可以利⽤蒙特卡罗的⽅法或时间差分的⽅法得到值函数。
注意，这时的值函数其实是⼀个表格。对于状态值函数，其索引是状态；对于⾏为值函数，其索引是状态-⾏为对。值函数的迭代更新实际上就是这张表的迭代更新。因此，之前讲的强化学习算法⼜称为表格型强化学习。对于状态值函数，其表格的维数为状态的个数 ，其中 为状态空间。若状态空间的维数很⼤，或者状态空间为连续空间，此时值函数⽆法⽤⼀张表格来表⽰。这时我们需要利⽤函数逼近的⽅法表⽰值函数，如图6.1所⽰。当值函数利⽤函数逼近的⽅法表⽰后，可以利⽤策略迭代和值迭代⽅法构建强化学习算法。

2. 试着用DQN方法玩雅利达游戏

3. 试着比较DQN及其变种的效果

4. 修改神经网络的优化方法并比较效果

9 基于确定性策略搜索的强化学习方法

9.2 习题

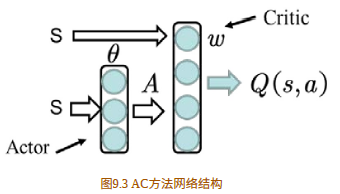
2.AC算法的⽹络结构是什么？

AC 算法包括两个同等地位的元素，⼀个元素是 Actor 即⾏动策略，另⼀个元素是Critic策略即评估，这⾥是指利⽤函数逼近⽅法估计值函数。

我们先看看随机策略AC的⽅法。

随机策略的梯度为

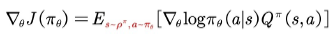
如图 9.3 所⽰，其中 Actor ⽅法⽤来调整θ值；Critic ⽅法逼近值函数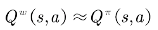其中w为待逼近的参数，可⽤TD学习的⽅法评估值函数。

本文转自 https://blog.csdn.net/weixin_35764841/article/details/102416510，如有侵权，请联系删除。