javaScript实现动态规划(Dynamic Programming)01背包问题
前言
动态规划(Dynamic Programming,DP)是运筹学的一个分支,是求解决策过程最优化的过程。
问题描述
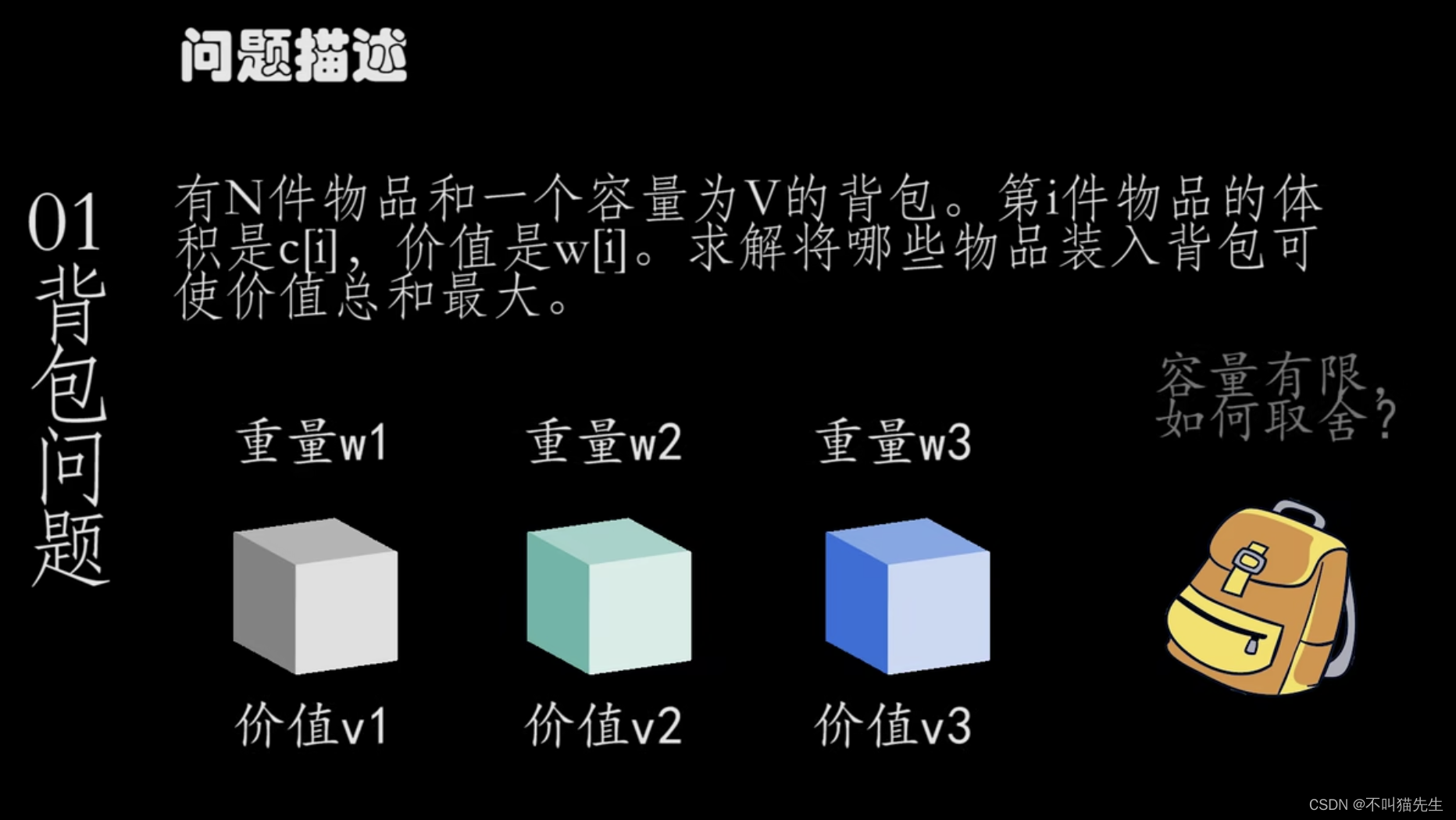
01背包问题是一个经典的算法问题,简单来说就是一个包要装许多水果,水果有体积和大小两个属性,怎么把包装满价值最大(最值钱)。
专业描述问题:有N件物品和一个容量为v的背包,第i件物品的体积是c[i],价值是w[i],求将那些物品怎么装进背包使价值总和最大。
注意:物品只能取一次或者不取,不能多次获取
原理
f(i,c) = math.Max( f(i-1,c),(f(i-1,c-w[i]) + v[i])) //取最大值
枚举第i个物品,选还是不选
- 选:容量减少了w[i]
- 不选:剩余容量不变
然后需要考虑在剩余容量为c的情况下,从前i个物品中能得到的最大价值和。
- 不选:在剩余容量为c时,从前i-1个物品中获得最大价值和
- 选:在剩余容量为c-w[i]的时候,从前i-1个物品中获取最大价值和
最终取两者的最大值
案例
背包的最大容量为6,其他物品信息如下:
| 体积 | 价值 | |
|---|---|---|
| 葡萄 | 2 | 3 |
| 矿泉水 | 3 | 5 |
| 西瓜 | 4 | 6 |
根据背包容量从0-6以及物品,初始化表格。
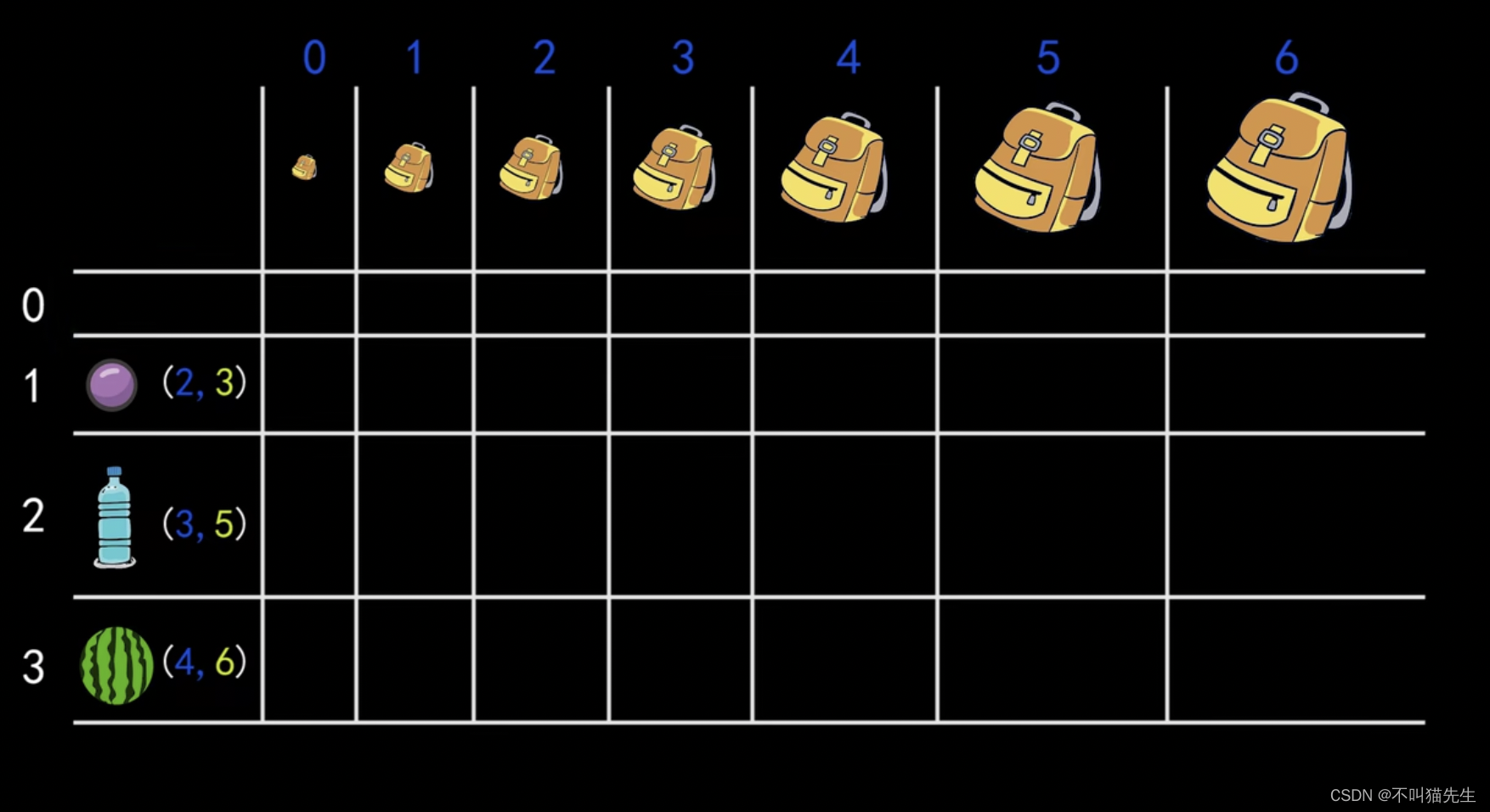
表格中的单元格代表的是什么意思呢?以图中为例:第2行第4列的单元格表示背包容量最大为3的情况下,对前2类物品进行选择,使得背包的价值为最大值。
第i行第j列的单元格 表示背包容量最大为j的情况下,对前i类物品进行选择,能使得背包的价值为最大值。每个单元格都是当前条件下的最优解,表格的右下角的单元格就是最优解。
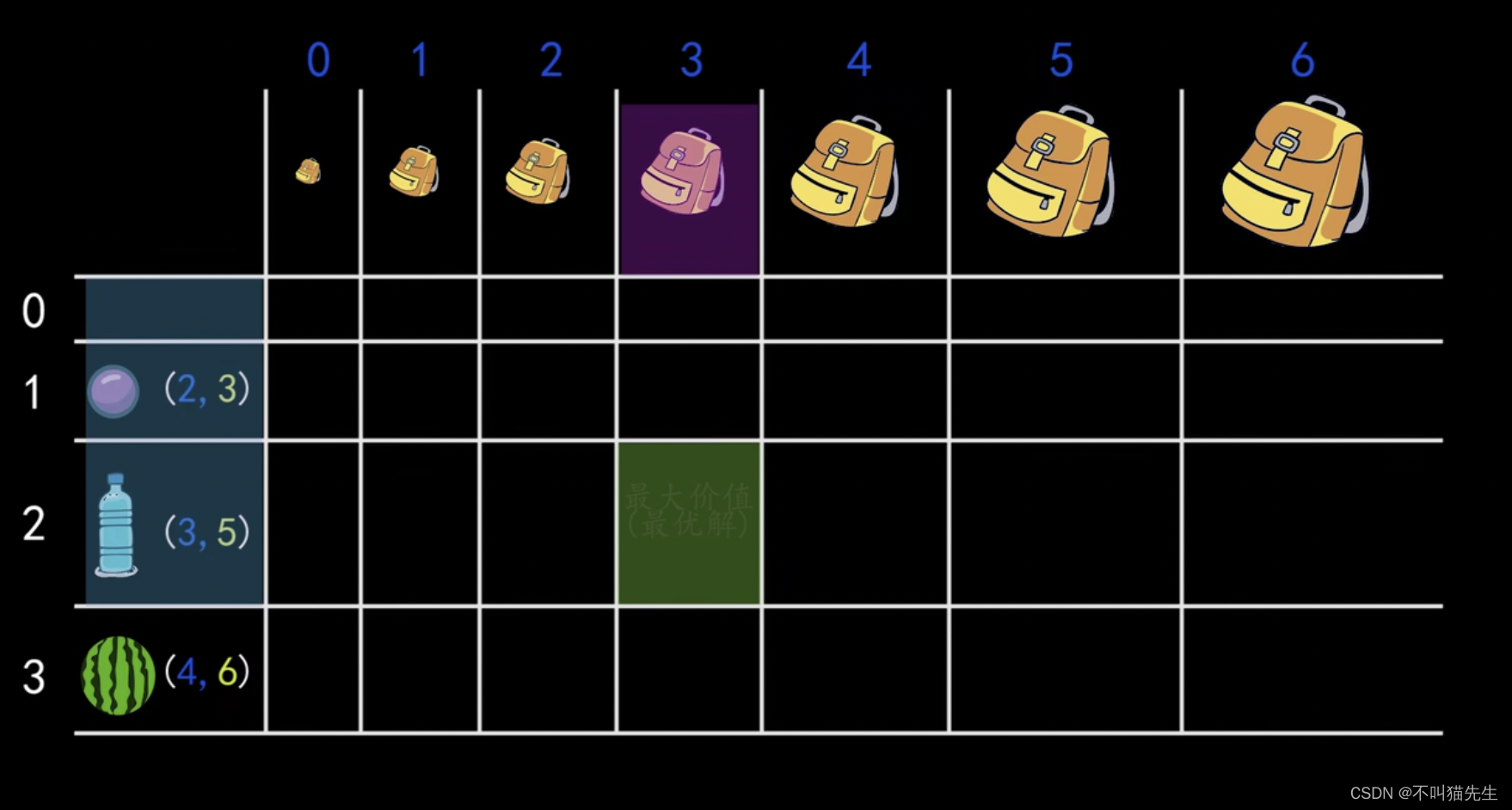
第0行在任何容量体积下,没有任何物品,所以都为0,即前0个物品装进背包的价值都为0 。
对于第0列来说,因为背包容量为0,所以任何物品都不能装进背包,所以价值都为0,即第0列数据都为0。虽然是第0行第0列,但是都是在各自限制条件下的最优解。
分析第一行第一列的单元格
在背包容量最大为1的条件下,对前一种物品取舍选择后获得的最大价值。在考虑单元格的时候需要进行判断:新纳入考量的物品是否超过背包的总容量。第一行第一列这里新纳入的物品为葡萄,葡萄的体积(2)大于背包体积(1),所以放不进去。
我们已经计算出不考虑葡萄时候,最大价值为0 ,此时我们的最优解继承自其上方单元格也就是(0,1)的值分析第一行第二列的单元格
在背包容量最大为2的条件下,对前一种物品取舍选择后获得的最大价值。此时物体体积等于背包体积,此时不能继承上方单元格的值,也就是不能继承(0,2)的数据。此时需要比较两种数据的大小:- 不考虑新纳入物品(也就是说不考虑此时葡萄获得的最优解),这个最优解为上方单元格的最优解(第0个物品在背包体积为2的情况的最优解:0)
- 背包容量为2的情况下,对前一种物品取舍选择后获得的最大价值,此时刚好可以放进背包,那么问题就变成了背包容量为0的情况下对前一种物品取舍选择后获得的最大价值 + 当前物品的价值(此时为葡萄🍇)。变成了背包容量为0的情况是通过当前背包容量(2) - 此时物品容量(2) = 0。
- 然后比较两者大小,取最大值
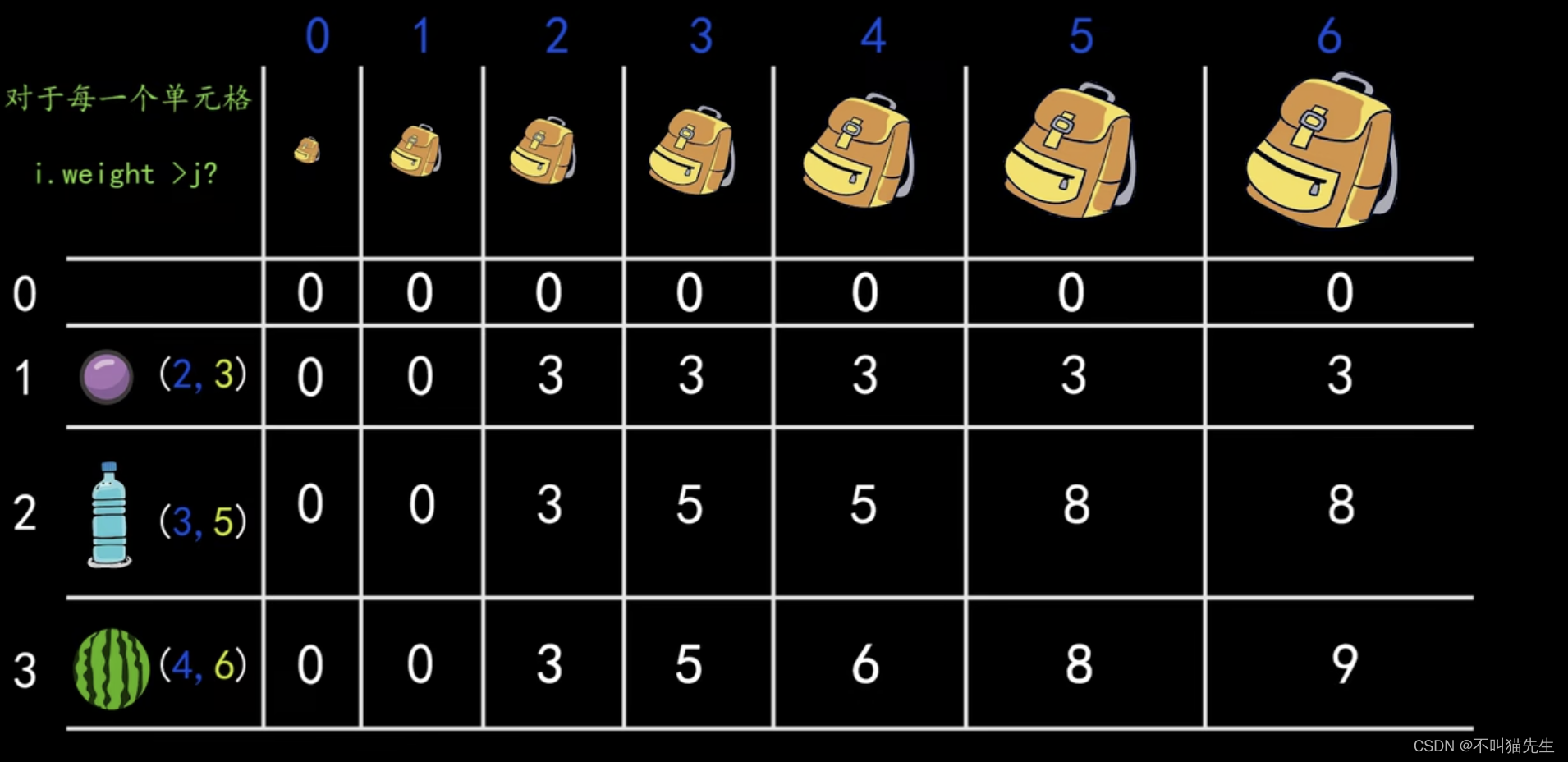
分析其他单元格与上面类似,最终得到右下方单元格的值(最优解)
最终计算完得到以下结果

<script>
let weight = [2, 3, 4];//物体体积
let value = [3, 5, 6];//物体价值
let bagWeight = 6;//背包最大容纳量
function bagProblem(weight, value, bagWeight) {
// 初始化dp,生成二维数组,长度为物体种类总长度,里面的数组长度为(背包最大容纳量+1)
const dp = new Array(weight.length + 1).fill(0).map(() => new Array(bagWeight + 1).fill(0));
//此时dp为
//[[0, 0, 0, 0, 0,0, 0],
//[0, 0, 0, 0, 0,0, 0],
//[0, 0, 0, 0, 0,0, 0],
//[0, 0, 0, 0, 0,0, 0],
//[0, 0, 0, 0, 0,0, 0]]
// 设置第一个物品在背包体积为(0-6)中的最优解
for (let j = weight[0]; j <= bagWeight; j++) { //i<= 4
dp[0][j] = value[0]
}
//此时dp为
//[[0, 0, 3, 3, 3,3,3],
//[0, 0, 0, 0, 0,0, 0],
//[0, 0, 0, 0, 0,0, 0],
//[0, 0, 0, 0, 0,0, 0],
//[0, 0, 0, 0, 0,0, 0]]
for (let j = 0; j <= bagWeight; j++) { //0<=4 j为包的最大重量
for (let i = 1; i < weight.length; i++) { // 1<=3 i为三个包的索引
if (j < weight[i]) { // 包的最大重量 < 第i个包的重量,此时最优解为继承上一个单元格
dp[i][j] = dp[i - 1][j] //dp[i][j]
} else {
// 包的最大重量 < 第i个包的重量
//Math.max(前一条数据最优解,(此时容纳量-当前选择物体的容纳量)的最优解 + 此时物体的价值)
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
}
}
}
return dp[weight.length - 1][bagWeight]
}
bagProblem(weight, value, bagWeight)
console.log(bagProblem(weight, value, bagWeight))
</script>
- 点赞
- 收藏
- 关注作者


评论(0)