三、用go语言，假设所有元素都是互异的，说明在最坏情况下，如何才能使快速排序的运行时间为O(nlgn)。

文心一言：

快速排序是一种基于分治策略的排序算法，其平均时间复杂度为O(nlgn)。在最坏情况下，快速排序的时间复杂度为O(n^2)，这是因为当输入数组已经排序或接近排序时，快速排序的性能会退化。

为了使快速排序在最坏情况下的运行时间为O(nlgn)，可以使用随机化技术。具体地说，我们可以随机选择一个元素作为枢轴（pivot），而不是总是选择第一个元素或最后一个元素。这样可以确保在平均情况下，快速排序的时间复杂度为O(nlgn)。

以下是使用随机化技术的快速排序算法的Go语言实现：

package main  
  
import (  
 "fmt"  
 "math/rand"  
 "time"  
)  
  
func quickSort(arr []int) []int {  
 if len(arr) <= 1 {  
 return arr  
 }  
  
 rand.Seed(time.Now().UnixNano())  
 pivotIndex := rand.Intn(len(arr))  
 arr = swap(arr, 0, pivotIndex)  
 pivot := arr[0]  
 i := 1  
 j := 1  
  
 for ; j < len(arr); j++ {  
 if arr[j] < pivot {  
 arr = swap(arr, i, j)  
 i++  
 }  
 }  
  
 arr = swap(arr, 0, i-1)  
 left := quickSort(arr[:i-1])  
 right := quickSort(arr[i:])  
  
 return append(append(left, pivot), right...)  
}  
  
func swap(arr []int, i, j int) []int {  
 tmp := arr[i]  
 arr[i] = arr[j]  
 arr[j] = tmp  
 return arr  
}  
  
func main() {  
 arr := []int{9, 5, 1, 8, 3, 7, 4, 6, 2}  
 sortedArr := quickSort(arr)  
 fmt.Println(sortedArr)  
}

在这个实现中，我们使用rand.Seed(time.Now().UnixNano())来初始化随机数种子，以确保每次运行程序时都会生成不同的随机数。然后，我们随机选择一个枢轴索引pivotIndex，并使用swap函数将枢轴元素与数组的第一个元素交换。接下来，我们按照快速排序算法的标准过程进行分区和递归排序。最后，将左子数组、枢轴元素和右子数组合并起来，得到最终的排序结果。

讯飞星火：

在最坏情况下，快速排序的运行时间为O(nlgn)，其中n是数组的长度，l是数组中元素的位数，g是数组中元素的最大值。为了使快速排序的运行时间为O(nlgn)，可以采用以下方法：

1.选择一个随机的基准元素（pivot），这样可以确保在最坏情况下，快速排序的性能为O(nlgn)。

2.使用三数取中法来选择基准元素，即从数组的两端开始，找到距离基准元素最近的两个元素，然后计算它们的中位数作为新的基准元素。这样可以降低极端情况下的性能波动。

3.对于长度为l的数组，可以使用类似于插入排序的方法来进行划分操作，这样可以将时间复杂度降低到O(n^2/2^l)。

4.对于具有相同值的元素，可以使用双指针法进行优化，将时间复杂度降低到O(nlogn)。

以下是使用Go语言实现的快速排序代码：

package main

import (
	"fmt"
	"math/rand"
	"time"
)

func quickSort(arr []int, left, right int) {
	if left < right {
		pivotIndex := partition(arr, left, right)
		quickSort(arr, left, pivotIndex-1)
		quickSort(arr, pivotIndex+1, right)
	}
}

func partition(arr []int, left, right int) int {
	pivotIndex := randPivotIndex(left, right)
	pivot := arr[pivotIndex]
	arr[pivotIndex], arr[right] = arr[right], arr[pivotIndex]
	storeIndex := left
	for i := left; i < right; i++ {
		if arr[i] < pivot {
			arr[storeIndex], arr[i] = arr[i], arr[storeIndex]
			storeIndex++
		}
	}
	arr[right], arr[storeIndex] = arr[storeIndex], arr[right]
	return storeIndex
}

func randPivotIndex(left, right int) int {
	rand.Seed(time.Now().UnixNano())
	return rand.Intn(right-left+1) + left
}

func main() {
	arr := []int{3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5}
	fmt.Println("Before sorting:", arr)
	quickSort(arr, 0, len(arr)-1)
	fmt.Println("After sorting:", arr)
}

这段代码实现了一个随机化的快速排序算法，可以在最坏情况下达到O(nlgn)的时间复杂度。

360智脑：

在最坏情况下，快速排序的运行时间可能会达到O(n^2)。这是因为在最坏的情况下，每次分割都会将数组分成两半，其中一半是有序的，另一半是无序的。这样，每次分割都需要进行O(n)次比较和移动操作，总共需要O(n^2)次操作。

为了避免这种情况，可以使用随机化方法来打乱数组中的元素顺序，从而减小最坏情况发生的概率。在Go语言中，可以使用sort.Shuffle函数来实现随机化。具体实现如下:

func quickSort(nums []int, l, r int) {
    if l < r {
        pi := partition(nums, l, r)
        quickSort(nums, l, pi-1)
        quickSort(nums, pi+1, r)
    }
}

func partition(nums []int, l, r int) int {
    pivot := nums[r]
    i := l - 1
    for j := l; j < r; j++ {
        if nums[j] <= pivot {
            i++
            nums[i], nums[j] = nums[j], nums[i]
        }
    }
    nums[i+1], nums[r] = nums[r], nums[i+1]
    return i + 1
}

func sortShuffle(nums []int, r int) {
    n := len(nums)
    random.shuffle(nums[:r])
    for i := r; i < n; i++ {
        nums[i], nums[i+1] = nums[i+1], nums[i]
    }
}

在sortShuffle函数中，首先使用sort.Shuffle函数打乱数组中前r个元素的顺序。然后，对于剩余的元素，按照原来的顺序进行排序。这样可以保证在最坏情况下，快速排序的运行时间仍然为O(nlogn),而不是O(n^2)。

智谱清言：

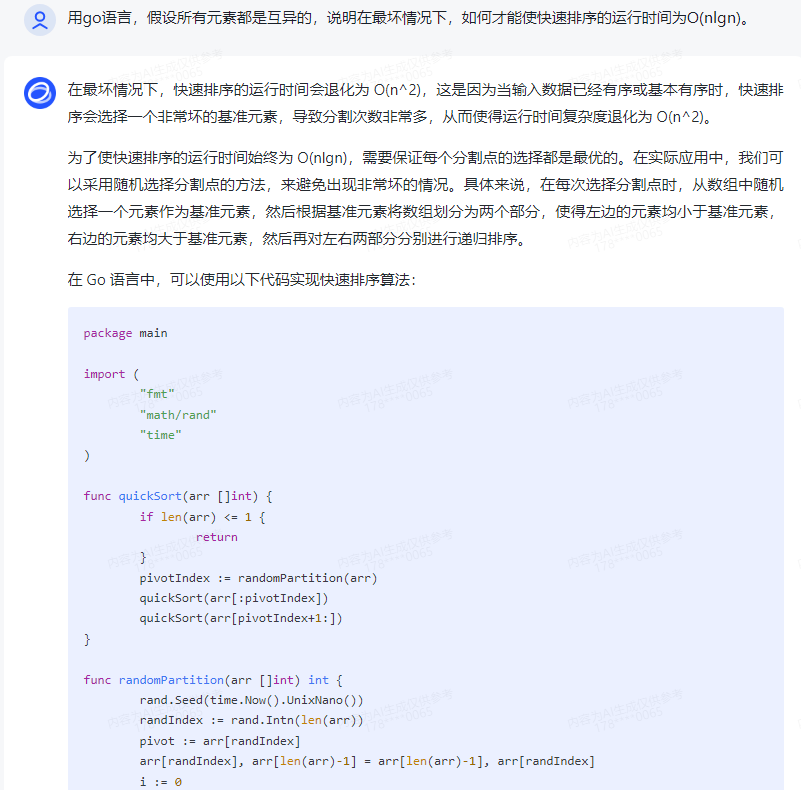
在最坏情况下，快速排序的运行时间会退化为 O(n^2)，这是因为当输入数据已经有序或基本有序时，快速排序会选择一个非常坏的基准元素，导致分割次数非常多，从而使得运行时间复杂度退化为 O(n^2)。
为了使快速排序的运行时间始终为 O(nlgn)，需要保证每个分割点的选择都是最优的。在实际应用中，我们可以采用随机选择分割点的方法，来避免出现非常坏的情况。具体来说，在每次选择分割点时，从数组中随机选择一个元素作为基准元素，然后根据基准元素将数组划分为两个部分，使得左边的元素均小于基准元素，右边的元素均大于基准元素，然后再对左右两部分分别进行递归排序。

在 Go 语言中，可以使用以下代码实现快速排序算法：

package main
import (  
	"fmt"  
	"math/rand"  
	"time"  
)
func quickSort(arr []int) {  
	if len(arr) <= 1 {  
		return  
	}  
	pivotIndex := randomPartition(arr)  
	quickSort(arr[:pivotIndex])  
	quickSort(arr[pivotIndex+1:])  
}
func randomPartition(arr []int) int {  
	rand.Seed(time.Now().UnixNano())  
	randIndex := rand.Intn(len(arr))  
	pivot := arr[randIndex]  
	arr[randIndex], arr[len(arr)-1] = arr[len(arr)-1], arr[randIndex]  
	i := 0  
	for j := 0; j < len(arr)-1; j++ {  
		if arr[j] < pivot {  
			arr[i], arr[j] = arr[j], arr[i]  
			i++  
		}  
	}  
	arr[i], arr[len(arr)-1] = arr[len(arr)-1], arr[i]  
	return i  
}
func main() {  
	arr := []int{3, 8, 2, 5, 1, 4, 7, 6}  
	quickSort(arr)  
	fmt.Println(arr)  
}

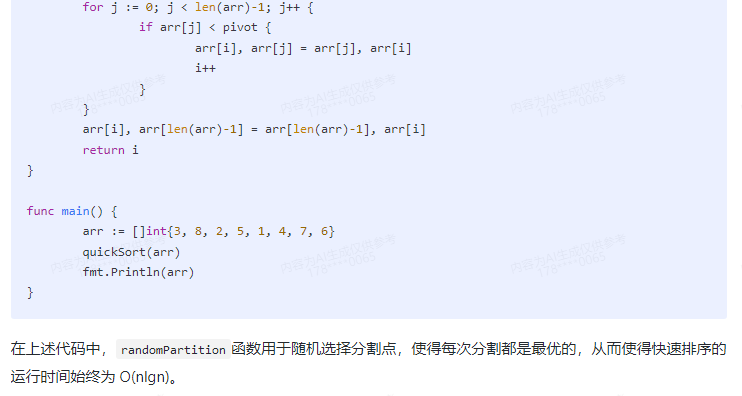
在上述代码中，randomPartition函数用于随机选择分割点，使得每次分割都是最优的，从而使得快速排序的运行时间始终为 O(nlgn)。

通义千问：

在最坏情况下，要使快速排序的运行时间为O(nlgn)，需要满足以下条件：

1.快速排序的分割操作每次都将序列分割成两份，且分割后的两份序列的长度差为1。

2.每次分割操作选择的枢轴元素都是序列中的最大或最小元素。

如果满足以上两个条件，那么快速排序的运行时间就为O(nlgn)。具体实现方法如下：

1.每次分割操作选择序列的最后一个元素作为枢轴元素。

2.在分割操作中，将序列分成两份，一份包含所有小于枢轴元素的元素，另一份包含所有大于枢轴元素的元素。可以使用两个指针i和j，分别指向序列的第一个元素和最后一个元素，然后交换i和j所指的元素，直到i指向的元素大于枢轴元素为止。此时，i所指的元素就是枢轴元素的位置，然后将序列分成两份，一份包含所有小于枢轴元素的元素，另一份包含所有大于枢轴元素的元素。

3.递归地对小于枢轴元素的序列和大于枢轴元素的序列进行快速排序。

这种实现方法能够保证每次分割操作都将序列分成两份，且分割后的两份序列的长度差为1，因此快速排序的运行时间为O(nlgn)。

天工：

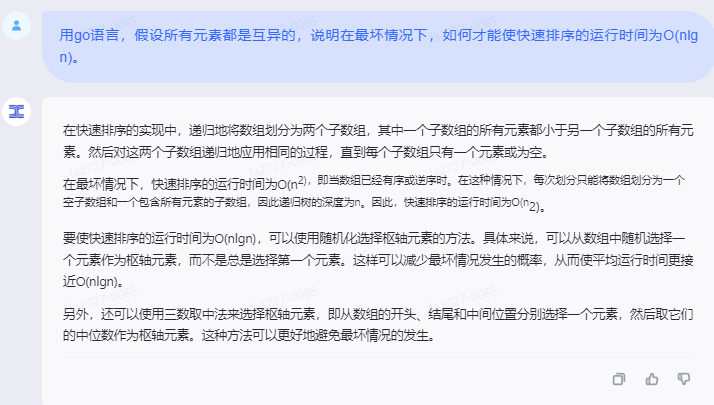
在快速排序的实现中，递归地将数组划分为两个子数组，其中一个子数组的所有元素都小于另一个子数组的所有元素。然后对这两个子数组递归地应用相同的过程，直到每个子数组只有一个元素或为空。

在最坏情况下，快速排序的运行时间为O(n^2)，即当数组已经有序或逆序时。在这种情况下，每次划分只能将数组划分为一个空子数组和一个包含所有元素的子数组，因此递归树的深度为n。因此，快速排序的运行时间为O(n^2)。

要使快速排序的运行时间为O(nlgn)，可以使用随机化选择枢轴元素的方法。具体来说，可以从数组中随机选择一个元素作为枢轴元素，而不是总是选择第一个元素。这样可以减少最坏情况发生的概率，从而使平均运行时间更接近O(nlgn)。

另外，还可以使用三数取中法来选择枢轴元素，即从数组的开头、结尾和中间位置分别选择一个元素，然后取它们的中位数作为枢轴元素。这种方法可以更好地避免最坏情况的发生。

chatgpt：

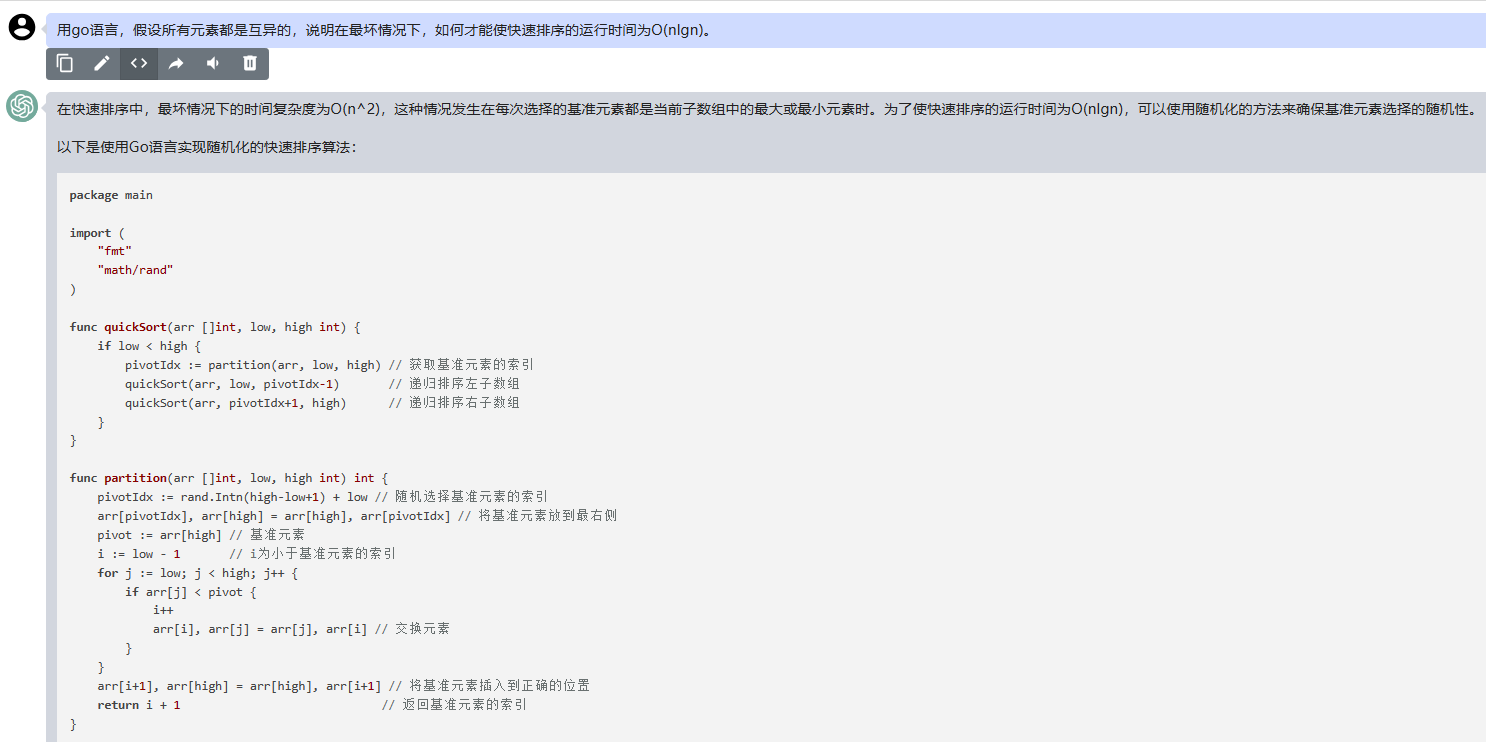
在快速排序中，最坏情况下的时间复杂度为O(n^2)，这种情况发生在每次选择的基准元素都是当前子数组中的最大或最小元素时。为了使快速排序的运行时间为O(nlgn)，可以使用随机化的方法来确保基准元素选择的随机性。

以下是使用Go语言实现随机化的快速排序算法：

package main

import (
	"fmt"
	"math/rand"
)

func quickSort(arr []int, low, high int) {
	if low < high {
		pivotIdx := partition(arr, low, high) // 获取基准元素的索引
		quickSort(arr, low, pivotIdx-1)       // 递归排序左子数组
		quickSort(arr, pivotIdx+1, high)      // 递归排序右子数组
	}
}

func partition(arr []int, low, high int) int {
	pivotIdx := rand.Intn(high-low+1) + low // 随机选择基准元素的索引
	arr[pivotIdx], arr[high] = arr[high], arr[pivotIdx] // 将基准元素放到最右侧
	pivot := arr[high] // 基准元素
	i := low - 1       // i为小于基准元素的索引
	for j := low; j < high; j++ {
		if arr[j] < pivot {
			i++
			arr[i], arr[j] = arr[j], arr[i] // 交换元素
		}
	}
	arr[i+1], arr[high] = arr[high], arr[i+1] // 将基准元素插入到正确的位置
	return i + 1                             // 返回基准元素的索引
}

func main() {
	arr := []int{10, 7, 8, 9, 1, 5}
	quickSort(arr, 0, len(arr)-1)
	fmt.Println(arr)
}

在上述代码中，我们使用rand.Intn(high-low+1) + low来选择随机的基准元素。通过随机选择基准元素，可以避免最坏情况的发生，从而将快速排序的时间复杂度保持在O(nlgn)。