哈夫曼树概念：

哈夫曼树（Huffman Tree），也被称为最优二叉树（Optimal binary
tree），是根节点到叶子节点路径和最小的二叉树。是一种用于数据压缩的树形结构。它利用字符出现频率来构建一种编码方式，使得频率高的字符获得较短的编码，频率低的字符获得较长的编码。

概念和特点：

1. 最优性：哈夫曼树是一棵最优二叉树，其具有最小的平均编码长度。换句话说，它能够以最小的位数编码来表示数据。

2. 前缀编码：哈夫曼树的编码是一种前缀编码（Prefix Code）。这意味着没有一个字符的编码是另一个字符编码的前缀，使得编码的解码过程是唯一的。

3. 字符频率：构建哈夫曼树的关键在于字符的频率信息。频率高的字符在哈夫曼树中对应的路径较短，频率低的字符对应的路径较长。

4. 唯一性：对于给定的字符频率，哈夫曼树是唯一的。不同的字符频率会产生不同的哈夫曼树。

使用场景

哈夫曼树（Huffman Tree）是一种用于数据压缩和编码的树结构。它的主要使用场景包括以下几个方面：

1. 数据压缩：哈夫曼树被广泛应用于数据压缩算法中，例如文件压缩、图像压缩和音频压缩等。通过构建哈夫曼树，可以根据字符或符号出现的频率来生成对应的编码，将频率高的字符用较短的编码表示，从而实现数据的压缩。

2. 文件存储：在文件存储方面，哈夫曼树可以用于构建索引结构或搜索树，提高查找和访问文件的效率。例如在文件系统中，可以使用哈夫曼树构建文件的索引，并根据索引来快速查找和访问文件。

3. 数据传输：在数据传输过程中，哈夫曼树可以用于数据的压缩和加密。通过哈夫曼编码，可以将待传输的数据压缩成较小的数据包，并在传输过程中实现数据的解压缩和恢复。这在网络传输、通信系统和嵌入式系统中都有应用。

4. 数据库和搜索引擎：哈夫曼树可以用于数据库的索引优化和搜索引擎的倒排索引构建。通过利用哈夫曼树的编码特性，可以实现高效的数据检索和查询操作，提高数据搜索的速度和效率。

5. 数据加密和安全：哈夫曼树可以用于数据的加密和解密，通过构建哈夫曼编码表，可以实现对敏感数据的加密和解密操作，并提高数据的安全性和保密性。

总之，哈夫曼树在数据压缩、编码、存储和传输等领域具有广泛的应用，能够提高数据的效率、节省存储空间，并在数据处理和通信中起到重要的作用。
哈夫曼树的构建步骤：

6. 统计字符频率：根据给定的数据，统计每个字符出现的频率。

7. 构建优先队列：将每个字符及其频率封装成节点，并使用优先队列（如最小堆）来按照频率排序。

8. 构建哈夫曼树：将优先队列中频率最低的两个节点进行合并，生成一个新的内部节点，并将其插入回优先队列。重复此过程，直到只剩下一个节点，即哈夫曼树的根节点。

9. 生成编码：通过遍历哈夫曼树，沿着左子树走为0，右子树走为1，获得每个字符的编码。

10. 数据压缩与解压缩：利用生成的编码，将原始数据压缩成哈夫曼编码表示的二进制数据。在解压缩时，根据哈夫曼编码和哈夫曼树进行解码，还原原始数据。

哈夫曼树的思想被广泛应用于数据压缩、通信传输、文件存储等领域。通过构建最优编码方式，可以有效地减少数据的存储空间和传输带宽。

哈夫曼编码模板

#include <iostream>
#include <queue>
using namespace std;

// 哈夫曼树节点
struct HuffmanNode {
    char data;
    int frequency;
    HuffmanNode* left;
    HuffmanNode* right;

    HuffmanNode(char ch, int freq) {
        data = ch;
        frequency = freq;
        left = right = nullptr;
    }
};

// 比较函数，用于优先队列中的排序
struct Compare {
    bool operator()(HuffmanNode* a, HuffmanNode* b) {
        return a->frequency > b->frequency;
    }
};

// 建立哈夫曼树
HuffmanNode* buildHuffmanTree(priority_queue<HuffmanNode*, vector<HuffmanNode*>, Compare>& pq) {
    while (pq.size() > 1) {
        HuffmanNode* left = pq.top();
        pq.pop();

        HuffmanNode* right = pq.top();
        pq.pop();

        int sum_freq = left->frequency + right->frequency;
        HuffmanNode* parent = new HuffmanNode('$', sum_freq);

        parent->left = left;
        parent->right = right;

        pq.push(parent);
    }

    return pq.top();
}

// 打印哈夫曼编码
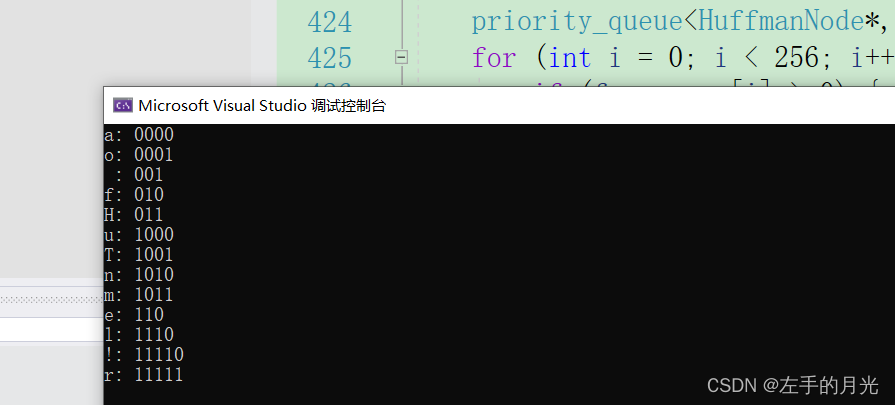
void printHuffmanCodes(HuffmanNode* root, string code) {
    if (root == nullptr)
        return;

    if (root->data != '$')
        cout << root->data << ": " << code << endl;

    printHuffmanCodes(root->left, code + '0');
    printHuffmanCodes(root->right, code + '1');
}

// 主函数
int main() {
    string input = "Hello Huffman Tree!";
    int frequency[256] = { 0 };

    // 统计字符频率
    for (char ch : input)
        frequency[ch]++;

    // 构建优先队列
    priority_queue<HuffmanNode*, vector<HuffmanNode*>, Compare> pq;
    for (int i = 0; i < 256; i++) {
        if (frequency[i] > 0) {
            HuffmanNode* node = new HuffmanNode(i, frequency[i]);
            pq.push(node);
        }
    }

    // 建立哈夫曼树
    HuffmanNode* root = buildHuffmanTree(pq);

    // 打印哈夫曼编码
    printHuffmanCodes(root, "");

    return 0;
}

哈夫曼练习题

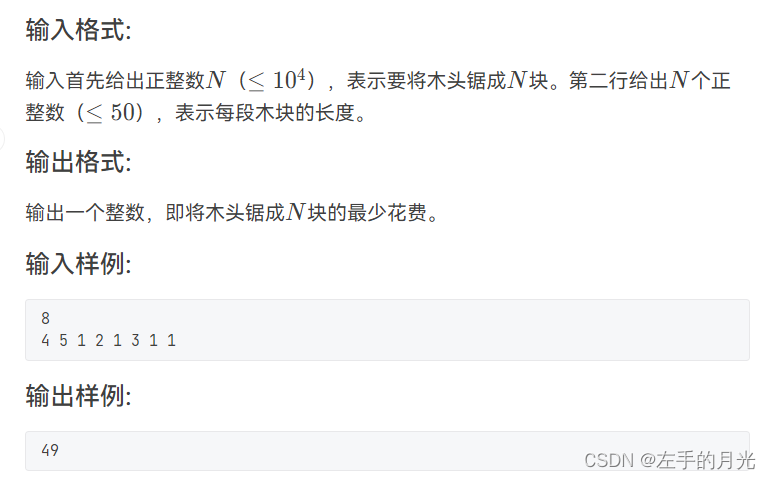
7-29 修理牧场

农夫要修理牧场的一段栅栏，他测量了栅栏，发现需要N块木头，每块木头长度为整数Li
​个长度单位，于是他购买了一条很长的、能锯成N块的木头，即该木头的长度是Li的总和。

但是农夫自己没有锯子，请人锯木的酬金跟这段木头的长度成正比。为简单起见，不妨就设酬金等于所锯木头的长度。例如，要将长度为20的木头锯成长度为8、7和5的三段，第一次锯木头花费20，将木头锯成12和8；第二次锯木头花费12，将长度为12的木头锯成7和5，总花费为32。如果第一次将木头锯成15和5，则第二次锯木头花费15，总花费为35（大于32）。

请编写程序帮助农夫计算将木头锯成N块的最少花费。

代码：

#include <iostream>
#include <queue>
#include <vector>
#include <functional>
using namespace std;
int main()
{
    int len, temp, min1, min2, sum = 0;
    //greater<int>升序排列，小的在队列出口
    priority_queue<int,vector<int>, greater<int> > q;
    cin>> len;
    for (int i = 0; i < len; ++i) {
        cin >> temp;
        q.push(temp);
    }
    while (q.size()>1 ){
        min1 = q.top();
        q.pop();
        min2 = q.top();
        q.pop();
        //sum代表根节点到每个叶子节点的最小和
            sum = sum + min1 + min2;
        q.push(min1 + min2);
    }
    cout << sum;
    return 0;
}