LeetCode刷题笔记
目录
1937.扣分后的最大分
思路：动态规划
1.先遍历出points数组的第一行，放入dp数组，因为第一行不需要通过上面的计算结果来求最大值。
2.如果dp数组挨个去加当前行的每一列，再求最大值，则肯定超时。
3.所以对于当前行的当前列points[i][j],我们可以求出Math.max(max - 1,dp[i - 1][j]),其中max为i - 1行中，j这一列前面的列的最大值，我们从j = 0开始，总是能求出max的值，max - 1即为所求的前缀，最大值，然后通过前缀最大值和dp[i - 1][j]比较。
4.考虑到i - 1这一行，有可能最大值出现在后缀列，所以通过同样的方法，我们求出后缀列与dp[i - 1][j]作比较，同时与前缀列的dp[i][j]作比较。。
代码:
/*********************************************
状态转移方程：
f[i][j]=max{f[i−1][x]-∣j−x∣}+points[i][j]
优化：
j>=x时
f[i][j]=max{f[i−1][x]+x∣}+points[i][j]-j
j<=x时
f[i][j]=max{f[i−1][x]-x∣}+points[i][j]+j
**********************************************/
class Solution {
public:
long long maxPoints(vector<vector<int>>& points) {
int m=points.size(); //行数
int n=points[0].size(); //列数
vector<long long> end(n); //建立保存状态的数组
for(int i=0;i<m;i++){ //遍历每一行
vector<long long> temp(n); //保存某一行的数据
long long best=LLONG_MIN;
//best存储上一行，并且小于等于当前列的最大值,即max{f[i−1][x]+x∣}
for(int j=0;j<n;j++){ //正序遍历,每次j++保证j>x;
best=max(best,end[j]+j);
temp[j]=best+points[i][j]-j; //第i行第j列正序的最大值
}
best=LLONG_MIN;
for(int j=n-1;j>=0;j--){ //倒叙序遍历,每次j--保证j<x;
best=max(best,end[j]-j);
//best存储上一行，并且大于等于当前列的最大值,即max{f[i−1][x]-x∣}
temp[j]=max(temp[j],best+points[i][j]+j);
//第i行第j列的最大值(正序倒叙取最大值)
}
end=move(temp); //把temp状态转移到end，end在本次循环存储上一行的状态
}
return *max_element(end.begin(), end.end());
}
};LLONG_MIN:long long的最小值
move()：状态转移
max_element():algorithm库中的函数，用于求[first，last）迭代器中的最大值，返回值是一个迭代器，需要解引用获得其值。
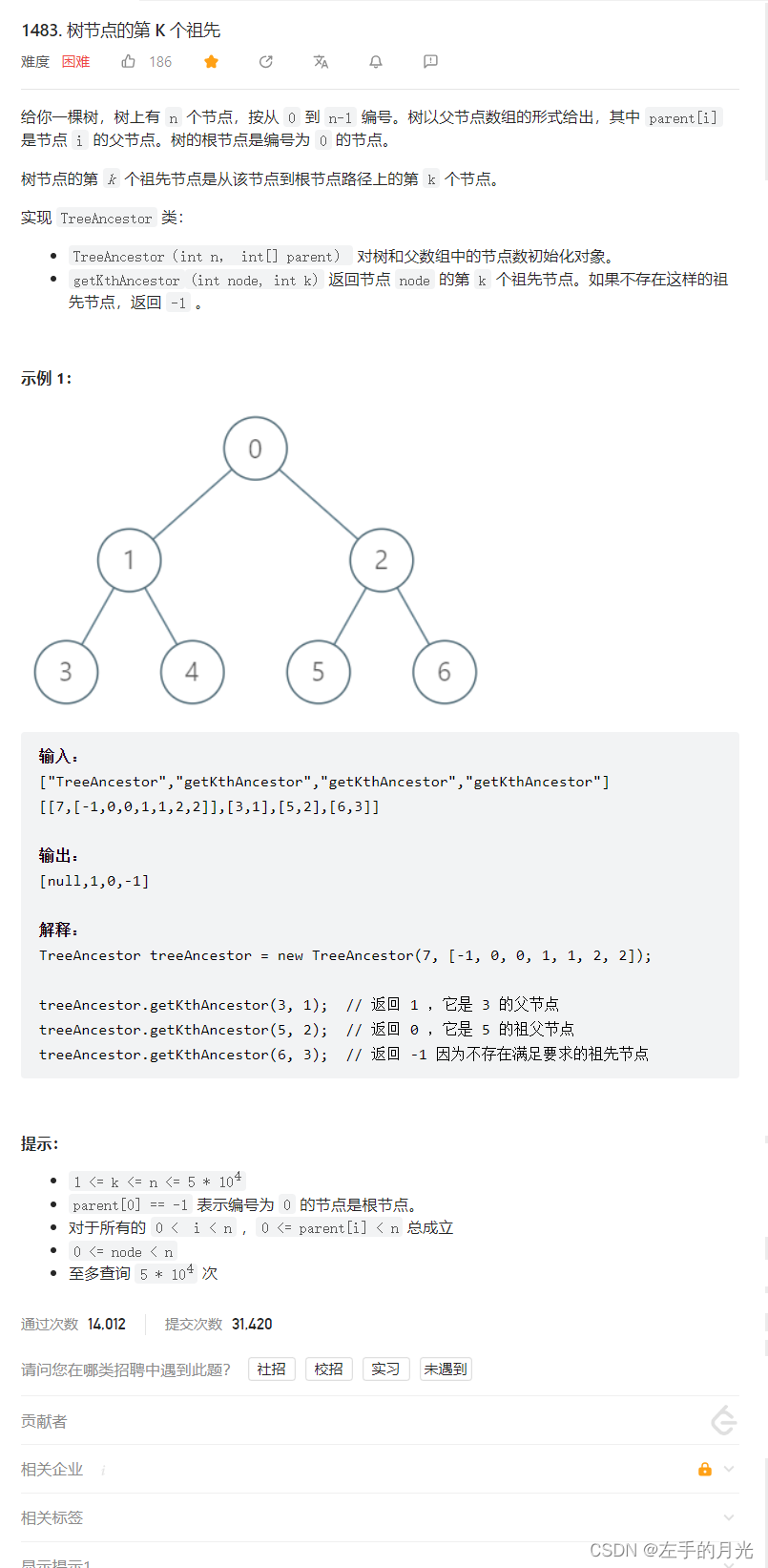
1483.树节点的第K个祖先
思路：
倍增的思路类似于动态规划，定义 ancestors[i][j] 表示节点 i 的第 2 的j次方个祖先。此题中，树最多有 50000 个节点，因此 ancestors 的第二维度的最大值可以设为 16。根据定义，ancestors[i][0]=parent[i]。状态转移方程是 ancestors[i][j]=ancestors[ancestors[i][j−1]][j−1]，即当前节点的第 个祖先的第 2的j−1次方个祖先。当第 2 的j次方个祖先不存在时，记为 −1。查询时，需要将 k 的二进制表示从最低位到最高位依次进行判断，如果第 j 位为 1，则节点 node 需要进行转移到 ancestors[node][j]，表示 node向祖先方向移动了 2的j次方次。直至遍历完 k 所有位或者 node 变为 −1。
代码：
class TreeAncestor {
public:
vector<vector<int>> ance;
const static int MAX_MAX=16;
TreeAncestor(int n, vector<int>& parent) {
ance=vector<vector<int>>(n,vector(MAX_MAX,-1));
for(int i=0;i<n;i++){
ance[i][0]=parent[i]; //初始化父节点
}
for(int j=1;j<MAX_MAX;j++){
for(int i=0;i<n;i++){
if(ance[i][j-1]!=-1){
ance[i][j]=ance[ance[i][j-1]][j-1]; //倍增
//ance[i][j]=ance[ance[i][j-1]][0]; //下一位是父节点
}
}
}
}
int getKthAncestor(int node, int k) {
for(int i=0;i<MAX_MAX;i++){
if((k>>i)&1){
node=ance[node][i];
if(node==-1){
return -1;
}
}
}
return node;
}
};
/**
* Your TreeAncestor object will be instantiated and called as such:
* TreeAncestor* obj = new TreeAncestor(n, parent);
* int param_1 = obj->getKthAncestor(node,k);
*/709.转换成小写字母
思路：枚举
遍历每一个字母，判断是否是大写字母，是大写字母，转化为小写字母。
/* 位运算（解题区的思路
大写变小写、小写变大写 : 字符 ^= 32;
大写变小写、小写变小写 : 字符 |= 32;
小写变大写、大写变大写 : 字符 &= -33;
eg：
65(A)->二进制表示为100 0001
32的二进制表示为 010 0000
100 0001|010 0000=110 0001->97(a)
*/
代码：
class Solution {
public:
string toLowerCase(string s) {
int len=s.size();
for(int i=0;i<len;i++){
if('A'<=s[i]&&s[i]<='Z'){
s[i]|=32;
}
}
return s;
}
};
/* 位运算（解题区的思路
大写变小写、小写变大写 : 字符 ^= 32;
大写变小写、小写变小写 : 字符 |= 32;
小写变大写、大写变大写 : 字符 &= -33;
eg：
65(A)->二进制表示为100 0001
32的二进制表示为 010 0000
100 0001|010 0000=110 0001->97(a)
*/
- 点赞
- 收藏
- 关注作者
评论（0）