计数排序详解

计数排序（非比较排序）

那到现在为止：

前面我们学的所有的排序算法，它们都是一大类的，即比较排序，就是我们在排序的过程中都对数据进行了大小的比较。 那接下来我们还要学习一个非比较排序——计数排序。 当然非比较排序肯定不止这一种，但我们这里重点给大家讲一下这个计数排序，因为计数排序在生活和工作中还是可能应用会比较多一点的，而且在找工作的时候也有可能会被考到。

接下来我们就一起来学习一下：

计数排序是一个非基于比较的排序算法，该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时，它的复杂度为Ο(n+k)（其中k是整数的范围），快于任何比较排序算法。

算法思想

<font color = blue>计数排序又称为鸽巢原理，是对哈希直接定址法的变形应用。

那具体的操作步骤是怎么样的呢？举个例子一起来看一下：

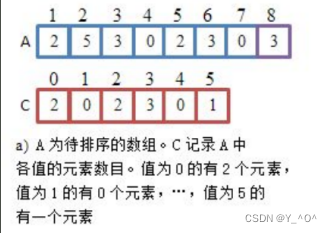
计数排序是这样搞的： 假如现在有这样一个数组待排序： 一共8个数。 对于一组待排序的数据，我们首先要做的是： 统计每个元素出现的次数保存到另一个数组中 那具体要怎么做？ 拿这组数据来说，我们可以先找出它的最大值，这里是5，那我们就开辟一个大小为5+1的数组C，这样最后一个下标值正好是5 ，该数组全部初始化为0。 然后，怎么做呢？ 遍历原数组，原数组的值是几，就让数组C下标为几的元素（初始为0）++，这样遍历一遍过后，<font color = red>数组C存的就是原数组每个元素出现的个数，下标的值就是对应的原数组中的数据。</font>

那统计好次数，下一步怎么做呢？

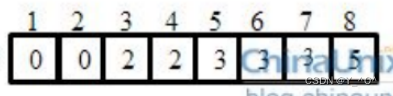
下面就可以进行排序了，怎么排？ 去遍历数组C，下标为0的的值是2，就说明0出现了两次，那就向原数组中（也是从下标为0位置开始），放两个0进去，继续遍历C，下标1位置值是0，就说明原数据没有1，继续向后，下标2的位置值是2，就接着向原数组放两个2... 依次类推，直到遍历完C数组。这时原数组的数据就是排好序之后的：

思考

刚才的例子我们很顺利就排好了，但是呢，还有一些问题值得我们思考一下：

如果待排序的数据大小差别非常大呢？ 比如说最小的数据是5，最大的是50000，那我们如果还按上面的思路进行排序的话是不是也得创建一个非常大的数组啊。 那这样空间的耗费是不是就太严重了啊。 所以呢？ 计数排序一般适用于范围相对集中的数据。

那除此之外，还有一个问题：

就算数据处的范围比较集中，但是数据都比较大怎么办： 比如是这样的，那我们也要开辟一个大小一百多的数组吗？ 是不是也有点不太合适。

思想优化

那这时我们就要想办法优化一下我们的思想了：

怎么优化呢？ 刚才我们统计次数其实是用的待排数据的一个绝对映射，什么意思呢？ 即待排的数据是几，它的次数就保存在了另一个数组下标为几的位置上。 那现在要优化，我们可以考虑使用数据的相对映射来搞： 什么意思呢？ 就拿这组数据来说： 如果还像上面那样的话，我们就得开一个大小为121的数组，因为最大值是120嘛，0到120 就是121个数嘛。 那这样前100个空间是不是都没用上啊。

那现在我们改变一下：

上面这组数据最大值max是120，最小值min是100，所以我们只需开一个大小为（max-min+1）的数组就够了。 那该数组的下标范围就是【0，20】了，如果和上面一样的话100就应该映射到下标为100的位置，那按我们现在的思路100是最小值，就映射到下标为0的位置。 即对于待排数组中的数组arr[i]，就映射到下标为arr[i]-min的位置就行了。

大家再思考一下：

用计数排序如果待排数组中有负数可以吗？ 如果用绝对映射是不是不行，假如有个-5，绝对映射的话-5的次数应该存在下标为-5的位置，这不就越界了，数组下标是不能为负的。 但我们现在用相对映射是不是就可以了。 假如有个负数-5，是最小的一个，那它映射到哪个位置，-5-min即-5-(-5)=0，🆗，下标为0的位置，是不是可以啊。 那剩下其它的步骤就还和原来一样了。

那其实这个优化的作用呢就是能少开一些空间。

代码实现

那我们接下来就来实现一下计数排序的代码：

首先第一步是什么：

1. <font color = red>找最大值最小值，确定我们要开的数组大小 大小是max-min+1，我们上面分析过了：

2. <font color = red>创建用来计数的数组并将全部元素初始化为0 当然这个地方不想手动初始化的话，也可以用calloc，它与malloc的区别就是可以自动将开好的空间初始化为0。

3. <font color = red>统计个数存入count数组

4. <font color = red>排序（遍历count数组按个数往原数组放数据）

5. <font color = red>释放malloc的数组

就写完了：

//计数排序
void CountSort(int* arr, int n)
{
    assert(arr);
    //找最值
    int max = arr[0];
    int min = arr[0];
    for (int i = 1; i < n; i++)
    {
        if (arr[i] > max)
            max = arr[i];
        if (arr[i] < min)
            min = arr[i];
    }
    int range = max - min + 1;
​
    //创建数组
    int* count = (int*)malloc(sizeof(int) * range);
    if (count == NULL)
    {
        perror("malloc fail");
        return;
    }
    memset(count, 0, sizeof(int) * range);
    /*int* count = (int*)calloc(range, sizeof(int));
    if (count == NULL)
    {
        perror("malloc fail");
        return;
    }*/
​
    //统计个数
    for (int i = 0; i < n; i++)
    {
        count[arr[i] - min]++;
    }
​
    //排序(遍历count数组按个数往原数组放数据）
    int j = 0;
    for (int i = 0; i < range; i++)
    {
        //count[i]就是每个数据出现的次数
        while (count[i]--)
        {
            arr[j] = i + min;
            j++;
        }
    }
​
    //释放malloc的数组
    free(count);
    count = NULL;
}

来测试一下： 来测一组带负数的： 没问题，🆗，那我们的计数排序就完成了。

计数排序特性总结

1. <font color = red>计数排序在数据范围集中时，效率很高，但是适用范围及场景有限。

2. <font color = red>时间复杂度：O(N + range)

3. <font color = red>空间复杂度：O(range)

4. <font color = red>稳定性：稳定