二叉树的链式结构及实现
二叉树的链式结构及实现
5.1 二叉树的链式结构
首先再回顾下二叉树的概念,二叉树是:
一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 或者由一个根节点加上两棵别称为左子树和右子树的二叉树组成
- 每个结点,只要不为空,就可以被分为根,左子树,右子树,因此,二叉树是递归定义的。
上面呢我们其实已经了解过二叉树的链式存储了,我们在一起来回忆一下:
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。
通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。
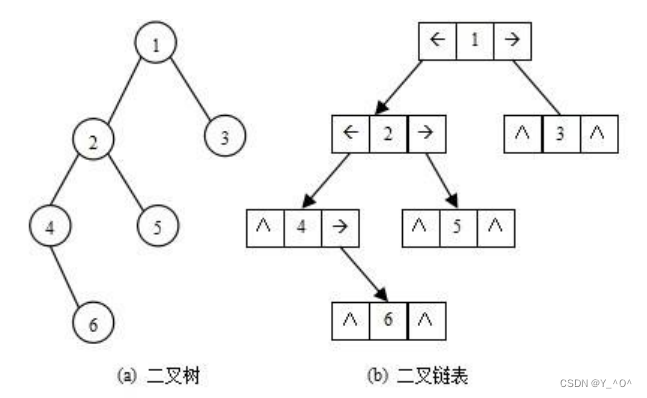
然后我们来学习一下二叉树的遍历:
二叉树遍历(Traversal)是按照某种特定的规则,依次对树中每个结点均做一次且仅做一次访问。
访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,是二叉树上进行其它运算之基础。
5.2 二叉树的前、中、后序遍历
首先我们来学习二叉树的前、中、后序遍历。
前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前,即根,左子树,右子树。
中序遍历(Inorder Traversal ) ——访问根结点的操作发生在遍历其左右子树中间,即左子树,根,右子树。
后序遍历(Postorder Traversal ) ——访问根结点的操作发生在遍历其左右子树之后,即左子树,右子树,根。
1. 举例
下面我们举个栗子来帮助大家理解:
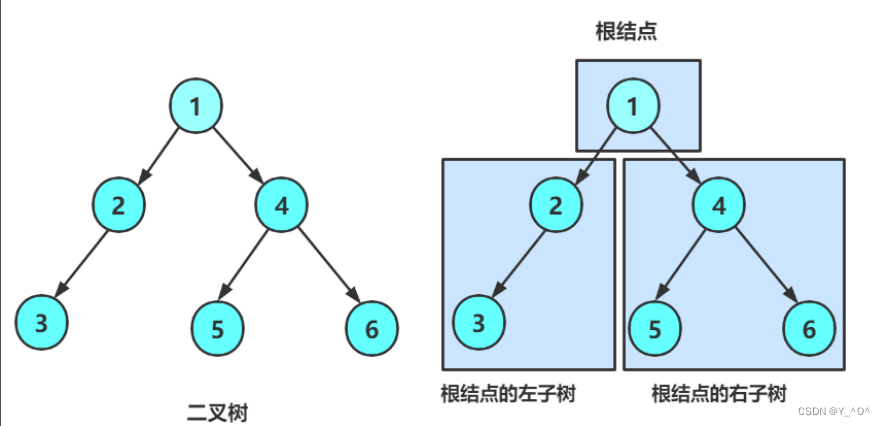
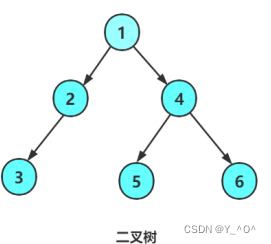
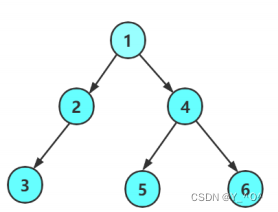
来看这棵二叉树:
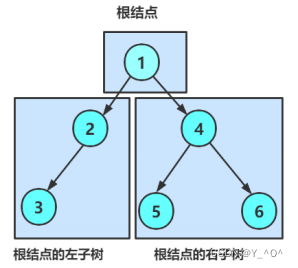
首先按照二叉树的概念可以将它分为3个部分:
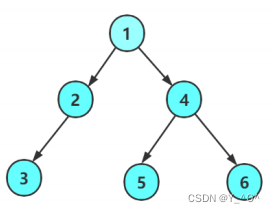
然后它的左右子树还可以再分:
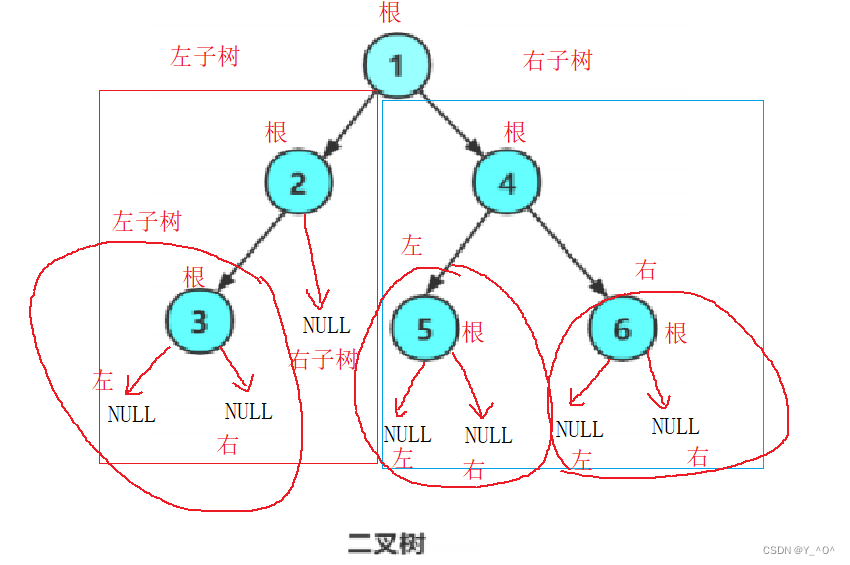
每棵子树都可以被分为根、左子树、右子树,一直分,一直分,直至被分成空(NULL)才停止。
那在遍历时也是一样,每棵子树都要按照相同的规则取遍历它的根,左子树和右子树,除非它是空。
下面我将对他进行前中后三种遍历操作:
首先看前序遍历(根、左子树、右子树):
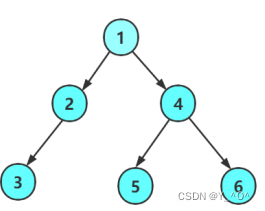
大家对照图,跟着我的思路走。
首先访问根是1:
1
然后1的左子树2,对左子树2同样先访问根
1 2
然后2的左子树3,同样先根
1 2 3
3的根完了是左子树,左子树是空:
1 2 3 NULL
,然后右子树,也是空:
1 2 3 NULL NULL
现在3整个访问完了,相当于2的左子树完了,然后是2的右子树,也是空:
1 2 3 NULL NULL NULL
现在2整个访问完了,相当于1的左子树完了,然后是1的右子树4,同样先根:
1 2 3 NULL NULL NULL 4
然后4的左子树5,同样先根:
1 2 3 NULL NULL NULL 4 5
根之后访问5的左子树,然后右子树,都是空:
1 2 3 NULL NULL NULL 4 5 NULL NULL
5整个访问完了,相当于4的左子树访问完了,然后是4的右子树6,照样先根:
1 2 3 NULL NULL NULL 4 5 NULL NULL 6
然后是6的左子树,然后右子树,都是空:
1 2 3 NULL NULL NULL 4 5 NULL NULL 6 NULL NULL
当然有时候为空的话我们可以省略,那就是这样:
1 2 3 4 5 6
然后是中序和后序:
中序后序我就不像上面那样详细解释了,相信如果大家仔细把上面前序理解透了,中序和后序就没啥问题了:
中序(左子树、根、右子树):
NULL 3 NULL 2 NULL 1 NULL 5 NULL 4 NULL 6 NULL
后序(左子树、右子树、根):
NULL NULL 3 NULL 2 NULL NULL 5 NULL NULL 6 4 1
大家仔细思考写一写,然后对照一下。
2. 代码实现(递归方式)
那如果现在给我们一棵二叉树,我们要对它进行前中后序遍历,代码怎么写?
因为二叉树是递归定义的,所以,用递归来实现也是非常好的。
我们还来参照这棵二叉树,完成代码:
但是我们的代码写出来是对任意一棵二叉树都成立的。
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType val;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
先来看先序遍历:
首先我们要知道空树也是一棵二叉树,如果上来拿到的就是一棵空树,那就直接return,当然这还包含了另一种情况,就是对一棵二叉树的左右子树一直分,一直分,直到分成不可再分的空(NULL)也要结束了。
这两种情况我们可以放在一起,为空时我们可以不做处理,也可以打印一下“NULL”:
if (root == NULL)
{
printf("NULL ");
return;
}
然后就是不为空的情况了:
不为空的话前序遍历那就先访问根,我们就先打印一下根结点的值:
printf("%d ", root->val);
根之后是左子树,那左子树同样可以看成一棵二叉树分成根,左子树右子树。
那就可以看作与原问题规模类似的子问题,那就可以用递归了:
PrevOrder(root->left);
那接下来右子树也是同样的道理:
PrevOrder(root->right);
那就写好了:
//前序遍历
void PrevOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%d ", root->val);
PrevOrder(root->left);
PrevOrder(root->right);
}
代码看起来很简单,但是:
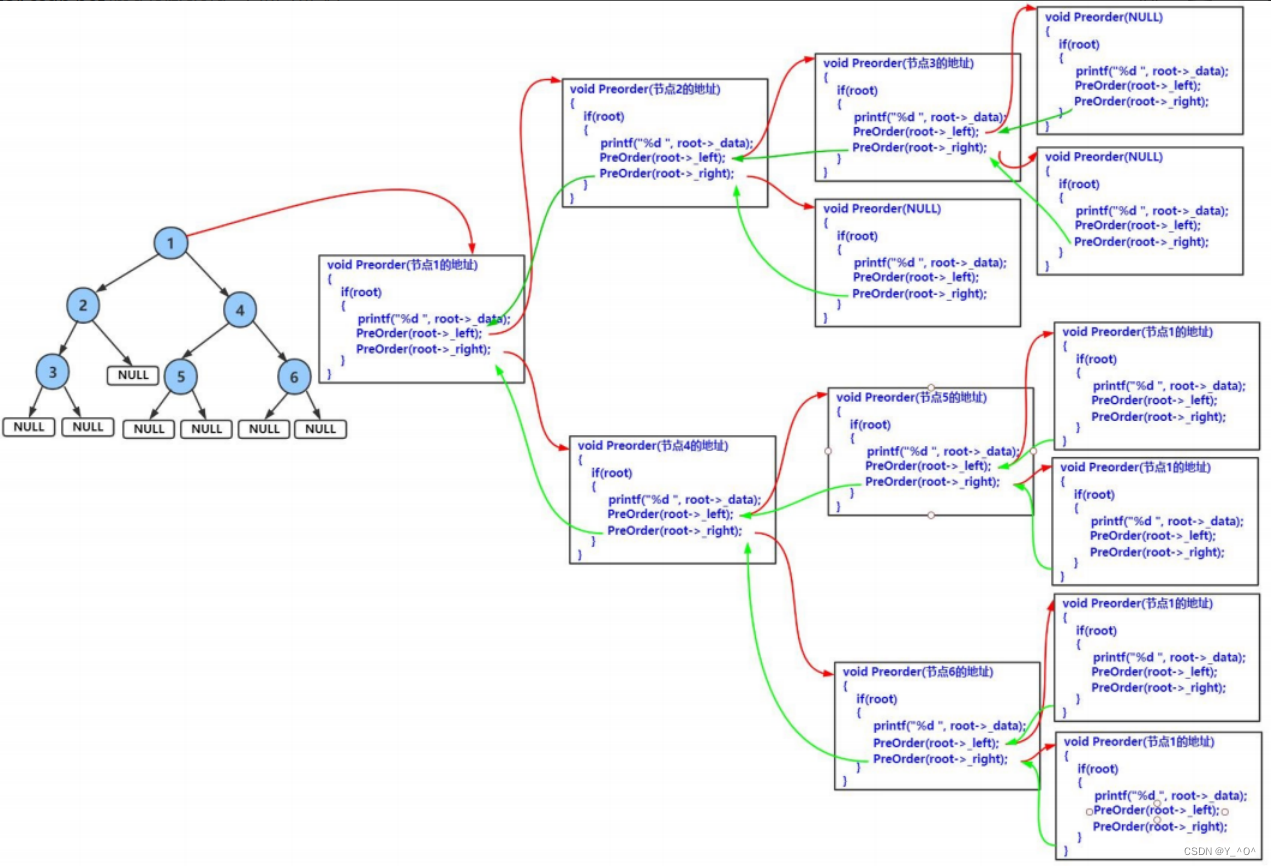
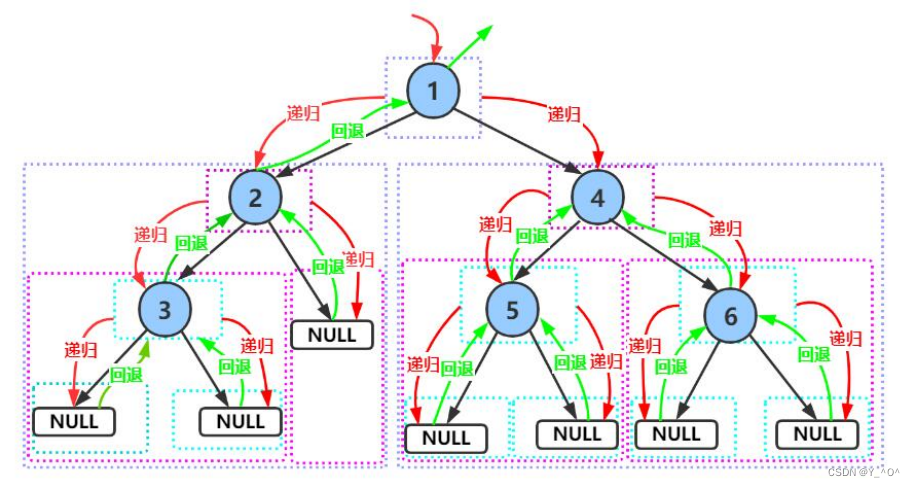
大家对这个递归过程可能还不是特别理解,下面画一下递归展开图帮助大家理解该递归的整个过程:
图中的代码实现跟我们的写法稍有差异,但其实是一样的。
当然,最好的方法还是大家自己去画一遍这个递归展开图,才能理解的更透彻。
那写好了我们来测试一下吧:
测试的话我们要先创建二叉树:
由于现在大家对二叉树结构掌握还不够深入,为了降低大家学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
我们就先手动创建一下上面那棵二叉树:
首先搞一个创建结点的函数:
BTNode* CreateBTNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
perror("malloc fail");
exit(-1);
}
node->val = x;
node->left = node->right = NULL;
return node;
}
然后我们创建对应的结点并按照上面的关系链接,并调用前序遍历函数
int main()
{
BTNode* n1 = CreateBTNode(1);
BTNode* n2 = CreateBTNode(2);
BTNode* n3 = CreateBTNode(3);
BTNode* n4 = CreateBTNode(4);
BTNode* n5 = CreateBTNode(5);
BTNode* n6 = CreateBTNode(6);
n1->left = n2;
n2->left = n3;
n1->right = n4;
n4->right = n6;
n4->left = n5;
PrevOrder(n1);
return 0;
}
运行代码看看结果是否正确:
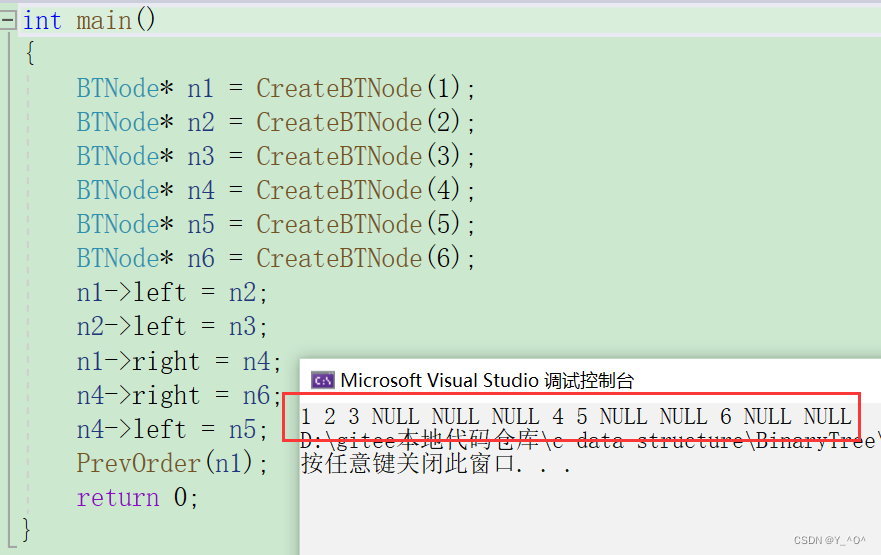
大家可以翻上去看一下,跟我们上面的结果是一样的。
🆗,那把前序搞明白了,后序和中序是不是就soeasy啊,变换一下代码的位置就搞定了,只是打印的顺序问题
//中序遍历
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
printf("%d ", root->val);
InOrder(root->right);
}
//后序遍历
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->val);
}
三个一块验证一下:
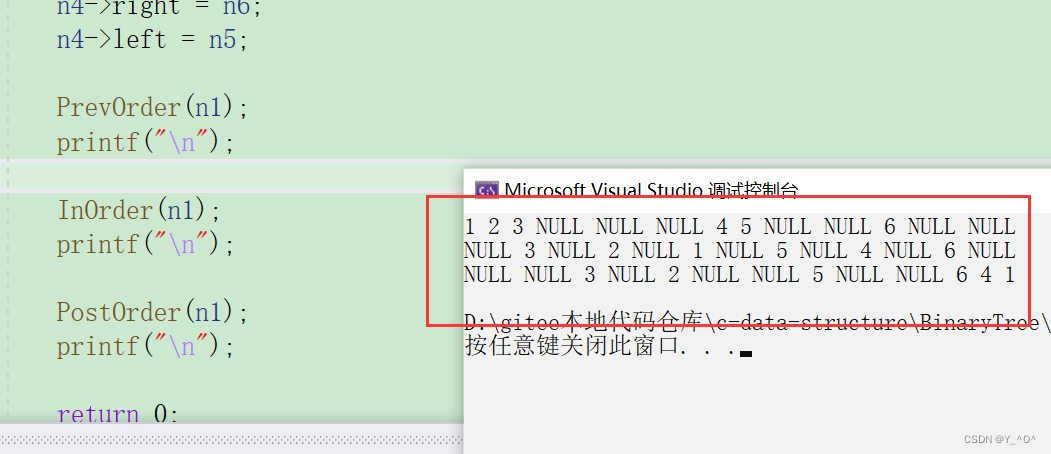


都是正确的。
除了这3种遍历方式,还有一个层序遍历,这个我们放在后面一点再讲,它是非递归的。
5.3 求二叉树结点个数
接下来我们来实现一个函数,要求它能够求出一棵二叉树的结点个数。
怎么搞?
好像不难,我们还是去遍历一遍二叉树(当然这里选择哪种遍历方式都可以),搞一个计数器,遍历到不是空的结点计数器++就行了嘛。
我们来实现一下:
//统计结点个数
int TreeSize(BTNode* root)
{
if (root == NULL)
return 0;
int size = 0;
size++;
TreeSize(root->left);
TreeSize(root->right);
return size;
}
代码就写好了,但这样写对不对呢?
其实简单分析一下就会发现这样写是会有问题的。
啥问题呢?
我们这里还是用了递归的方法,而size是我们定义在函数内部的一个局部变量,每次递归,都会建立新的函数栈帧,那size自然也会随着每次递归在新的函数栈帧中重新创建。
所以,每次递归,size都会重新定义,而每次++的也不是同一个size。
我们可以验证一下:

🆗,确实是错误的,有6个结点,但答案是1。
那如何解决这个问题呢?
我们可能会想到用全局变量或static修饰局部变量size(关于static的作用如果大家遗忘了或者不太清楚可以看之前写的这篇文章 )
链接: link
size被static修饰之后,就不会再存储到栈区了,而是会存储在静态区,静态局部变量的初值是在编译期间就指定的,所以运行期间每次递归都不会在重新创建变量size了,这样我们每次++的就是同一个size了。
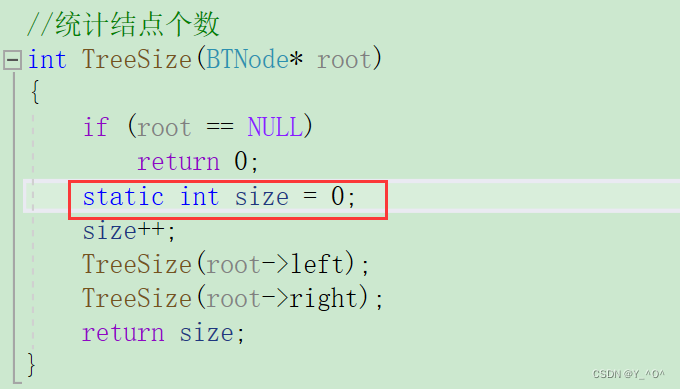
那这下是不是就行了呢?
哦豁,好像确实可以了。
但是,还会有一个问题:
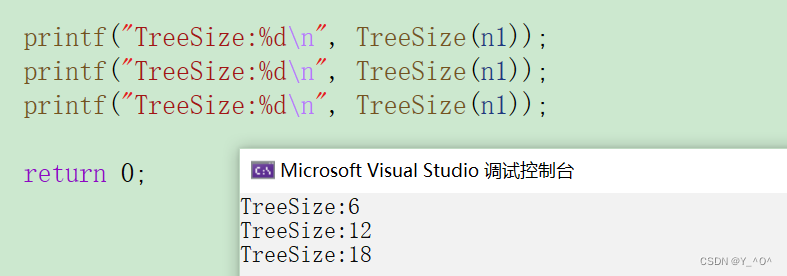
我们多调用几次Tree Size函数:
欸,为什么会这样?
因为size被static修饰后,其生命周期就是整个程序的生命周期,等到程序结束它才会被销毁,用全部变量也是这样。
所以,第一次调用结果没啥问题,后面再去调用,size也不会重新定义,因此结果才会越来越大。
而且static修饰的话中间程序不结束我们还没有办法给size重新赋初值。
如果确实想这样写的话,那就使用把size定义成全局变量,每次调用之前,将size手动置成0。
不过也不太好。
那有没有更优一点的方法来解决这个问题呢?
🆗,既然用static修饰也 不行,用全局变量也不太好,那我们干脆就不用计数器了。
那怎么弄?
直接算啊,如果为空就返回0 ,不为空至少有一个结点,那就返回1+左子树的结点个数+右子树的结点个数:
//统计结点个数
int TreeSize(BTNode* root)
{
return root == NULL ? 0 :
1 + TreeSize(root->left) + TreeSize(root->right);
}
一个三目运算符搞定!
来验证一下:
5.4 求叶子结点个数
接下来我们再来看一个问题,如何求一棵二叉树的叶子结点的个数?
首先回顾一下,啥是叶子结点:
那在链式结构中,就是它的左指针和右指针都指向空的结点。
比如在这棵二叉树中:
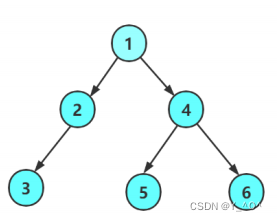
3,5,6就是3个叶子结点。
那思路是什么样的呢?
也很好办:
如果遇到空,就返回0;不是空,那就判断它是不是叶子结点,是的话返回一个1,不是的话,就返回它的左子树的叶子结点个数+右子树的叶子结点个数。
实现一下代码:
//统计叶子结点个数
int TreeLeafSize(BTNode* root)
{
if (root)
{
if (root->left == NULL && root->right == NULL)
return 1;
return TreeLeafSize(root->left) +
TreeLeafSize(root->right);
}
return 0;
}
验证一下:
是3个。
5.5 求二叉树高度/深度
我们接着往下看,如何求一棵二叉树的高度呢?
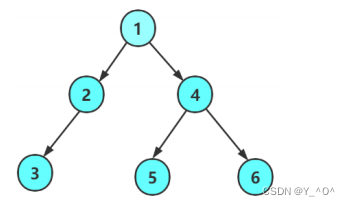
我们来讲一下思路:
首先给大家明确一下,这里我们认为空树高度为0(即认为根结点层次为1)。
那怎么搞呢?
如果是空树,就返回0;
如果不是空树,返回其左右子树高度中的最大值再+1(即加上当前根结点所处的这一层的1个高度)。
好像也不难,我们来实现一下代码:
//求二叉树的高度
int TreeHeight(BTNode* root)
{
if (root)
{
return
TreeHeight(root->left) > TreeHeight(root->right) ?
TreeHeight(root->left)+1 : TreeHeight(root->right)+1;
}
return 0;
}
写好了,测试一下,就来计算上面那棵树的高度:
确实是3。
代码逻辑确实没什么问题,也能正确计算出高度。
但是:
上面那种写法非常不好,看起来很简洁,很省事,但却导致计算效率大大降低。
为什么呢,我们来分析一下:
我们用了一个3目操作符,看起来很简洁。
但是问题出在哪里?
我们前面计算了左右子树的高度,但我们比较完没有保存,后面确定该表达式的最终结果时,又重新进行了计算。
大家可能会觉得这样的话不就算两遍而已,浪费时间不过比原来多一倍罢了。
🆗,我刚开始也是这样想的,但是问题远比你想象的严重很多,这个我用文字不好给大家描述清楚,大家可以自己尝试画一画递归展开图或者调试观察,这样写其实会造成大量大量的重复计算。
所以这样写真的很不好!
我们稍微改进一下,把前面算出来的值保存一下,就会好很多很多很多的。
//求二叉树的高度
int TreeHeight(BTNode* root)
{
if (root)
{
int LeftHeight = TreeHeight(root->left);
int RightHeight = TreeHeight(root->right);
return
LeftHeight > RightHeight ?
LeftHeight + 1 : RightHeight + 1;
}
return 0;
}
5.6 求第K层结点个数(k>=1)
再来,如何求一棵二叉树第K层的结点个数?
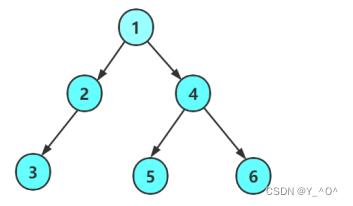
这个问题呢,如果大家第一次见,可能不太好想。
接下来我们讲一下思路:
还是分治思想:
首先如果是空树,不管是求第几层,都是0;
不为空的情况,如果k等于1,那不为空的二叉树,第一层肯定是1个结点,返回1;
如果K大于1,就返回相对于其左子树和右子树的第K-1层的结点个数。
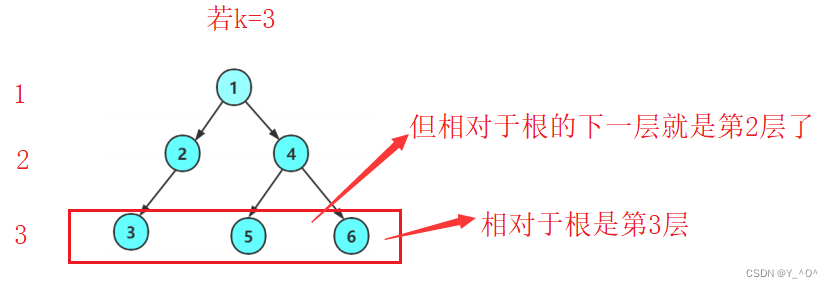
思路清楚了,我们来实现代码:
// 二叉树第k层节点个数
int TreeLevelKSize(BTNode* root, int k)
{
if (root)
{
if (k == 1)
return 1;
return TreeLevelKSize(root->left, k - 1)
+ TreeLevelKSize(root->right, k - 1);
}
return 0;
}
验证一下,第2层是2个结点:

5.7 查找值为x的结点
接着再来看一个问题:如何在一棵二叉树中查找值为X的结点,返回其地址?
假如现在我们要在这棵二叉树中查找值为5的结点。
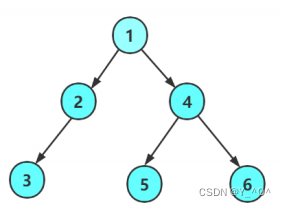
其实也很简单:
跟我们之前在链表中查找一个元素是一样的思路嘛。
这不过这里呢,我们还是用递归去搞。
怎么办?
如果这棵树不为空,那先判断根结点的值是不是等于我们要找的结点的值,等于的话,直接返回根结点地址;
如果根结点不是,那就判断左右子树能不能找到,左子树找不到就接着在右子树找;
左右子树都找不到,那就找不到了,返回NULL。
当然,上面是非空树的情况,如果是空树,那就不用找了,直接返回NULL。
接下来实现一下代码:
// 二叉树查找值为x的结点
BTNode* TreeFind(BTNode* root, BTDataType x)
{
if (root)
{
if (root->val == x)
return root;
BTNode* ret1 = TreeFind(root->left, x);
if (ret1)
return ret1;
BTNode* ret2 = TreeFind(root->right, x);
if (ret2)
return ret2;
return NULL;
}
return NULL;
}
看一下对不对:
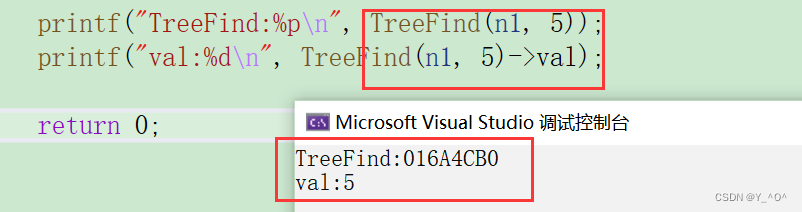
没问题。
5.8 二叉树的创建和销毁
1.创建
我们先来看一个题链接: link

这道题呢,给我们一个二叉树的前序遍历字符串,要求我们重构这棵二叉树,并对重构之后的二叉树进行中序遍历。
怎么做呢?
既然给我们的是前序遍历的字符串,那我们就遍历这串字符串,再以前序遍历的顺序去构建这棵二叉树就行了。
从头遍历给定的字符串,如果不是空,那我们就创建一个结点,结点的值就是对应的字符,然后去递归构建它的左子树,接着是右子树,并把构建好的左右子树的根结点链接在它的左右孩子指针上,如果遍历到字符“#”(根据题意表示空树),直接返回NULL即可。
然后我们实现一下代码:
#include <stdio.h>
#include <stdlib.h>
typedef char BTDataType;
typedef struct BinaryTreeNode
{
BTDataType val;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
} BTNode;
BTNode* CreateBTree(char* arr, int* pi)
{
if (arr[*pi] == '#') {
(*pi)++;
return NULL;
}
BTNode* root = (BTNode*)malloc(sizeof(BTNode));
if (root == NULL) {
perror("malloc fail");
exit(-1);
}
root->val = arr[*pi];
(*pi)++;
root->left = CreateBTree(arr, pi);
root->right = CreateBTree(arr, pi);
return root;
}
void InOrder(BTNode* root)
{
if(root)
{
InOrder(root->left);
printf("%c ",root->val);
InOrder(root->right);
}
}
int main() {
char arr[100];
scanf("%s", arr);
int i=0;
BTNode* root=CreateBTree(arr, &i);
InOrder(root);
return 0;
}
🆗,虽然OJ通过了,但是上面的程序还是有一些问题的,我们创建的二叉树没有销毁。
2. 销毁
那我们创建一棵二叉树,所有结点都是我们动态开辟出来的,所以程序结束之前我们肯定要将这些空间给释放掉的,即销毁二叉树,否则是不是就内存泄漏了啊。
那怎么做呢?
其实呢方销毁的法不止一种,但是比较优的方法是啥呢,是后序遍历去销毁这棵二叉树。
为啥后序比较好呢?
后序是最后访问根,也就是说我们先销毁左右子树,那如果用先序或中序,我们左右子树没销毁完就先把根给销毁了,但是我们找左右子树是不是要通过根结点的左右指针去找啊,这样就不太方便了。
那我们来实现代码:
//销毁
void TreeDestory(BTNode* root)
{
if (root)
{
TreeDestory(root->left);
TreeDestory(root->right);
free(root);
}
}
注意⚠:
这里我们用的是一级指针,传的是指向二叉树根结点的指针,所以销毁完最好将函数外面的root指针置空。
3.代码展示
#include <stdio.h>
#include <stdlib.h>
typedef char BTDataType;
typedef struct BinaryTreeNode
{
BTDataType val;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
} BTNode;
BTNode* CreateBTree(char* arr, int* pi)
{
if (arr[*pi] == '#') {
(*pi)++;
return NULL;
}
BTNode* root = (BTNode*)malloc(sizeof(BTNode));
if (root == NULL) {
perror("malloc fail");
exit(-1);
}
root->val = arr[*pi];
(*pi)++;
root->left = CreateBTree(arr, pi);
root->right = CreateBTree(arr, pi);
return root;
}
void InOrder(BTNode* root)
{
if(root)
{
InOrder(root->left);
printf("%c ",root->val);
InOrder(root->right);
}
}
//销毁
void TreeDestory(BTNode* root)
{
if (root)
{
TreeDestory(root->left);
TreeDestory(root->right);
free(root);
}
}
int main() {
char arr[100];
scanf("%s", arr);
int i=0;
BTNode* root=CreateBTree(arr, &i);
InOrder(root);
TreeDestory(root);
root=NULL;
return 0;
}
- 点赞
- 收藏
- 关注作者



评论(0)