🤵‍♂️ 个人主页: @计算机魔术师
👨‍💻 作者简介：CSDN内容合伙人，全栈领域优质创作者。

@[toc]

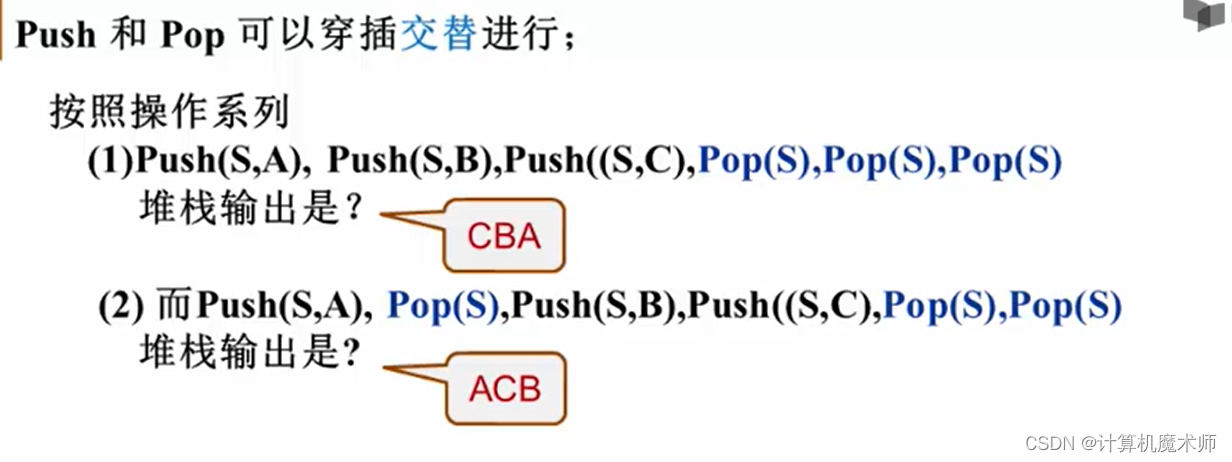
一、堆栈引入

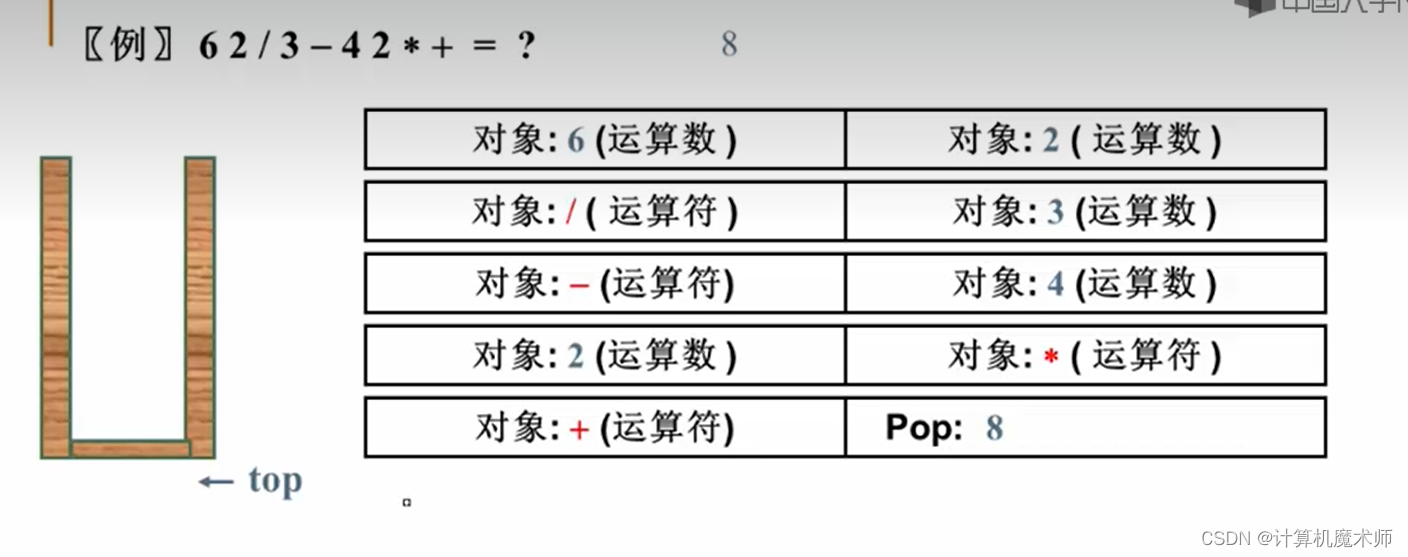
计算机如何进行表达式求值

由于表达式符号是有优先级的，所以这是难点之一

有以下两个表达式

显然后缀表达式更加简单，不用考虑优先级，演示一个例子

对这种求值策略我们有以下启示

这其实便是这节我们要讲的堆栈

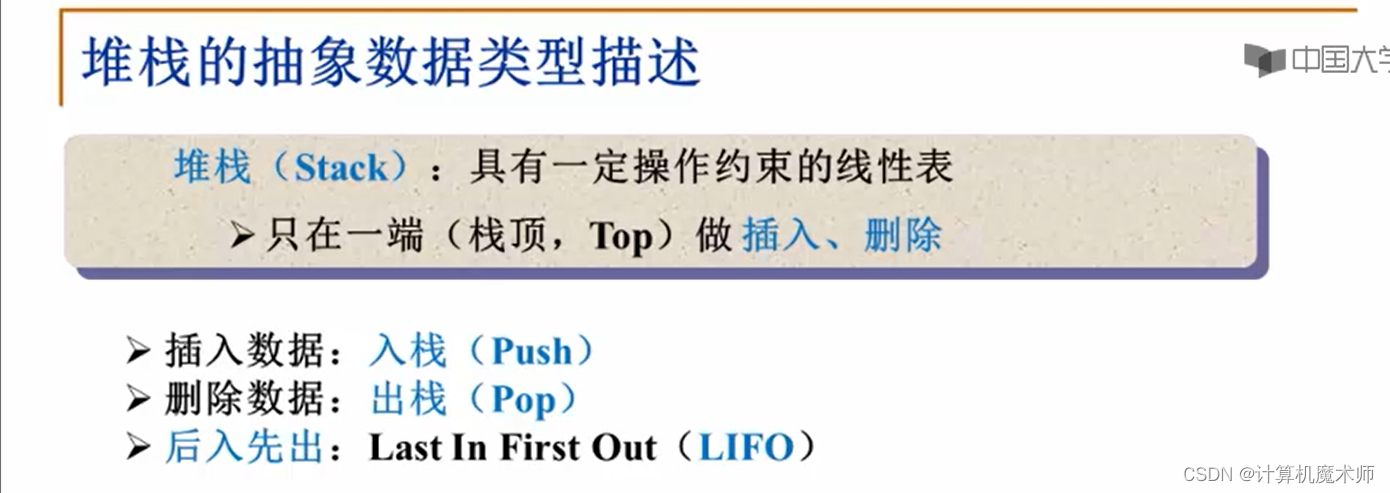
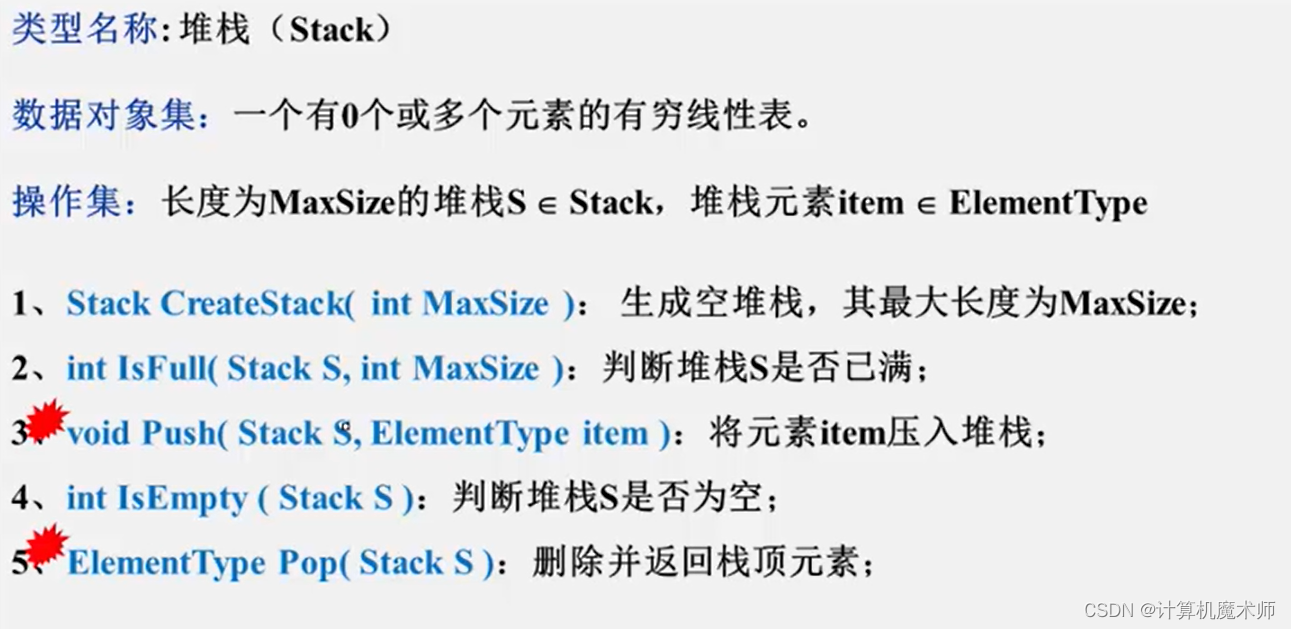
二、 堆栈的抽象数据类型描述

例如我们叠在一起的碗，在使用的清洗都和堆栈的规则

如下图是堆栈的变化图

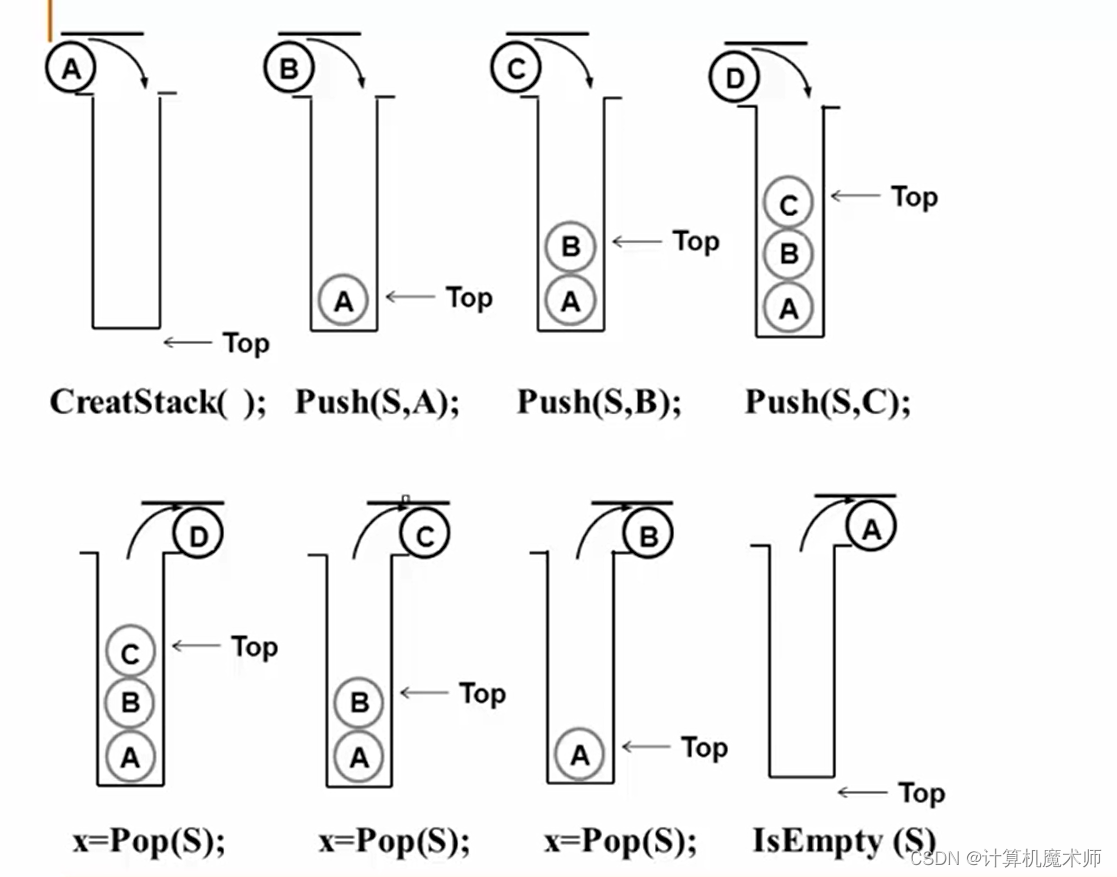
其中

三、堆栈的顺序存储实现

3.1主要操作的实现

入栈

出栈

我们看一个例子

如果简单的将数组对半分，同时从左边往右边存放，那么会出现一个堆栈栈满，一个未满的情况，而此时数组还有空间，我们换一种思路，将两边往中间放

我们看看他们的操作

入栈

出栈

四、堆栈的链式存储结构

由于单链表的性质，我们将链表头作为堆栈指针Top，这样方便与插入删除操作，

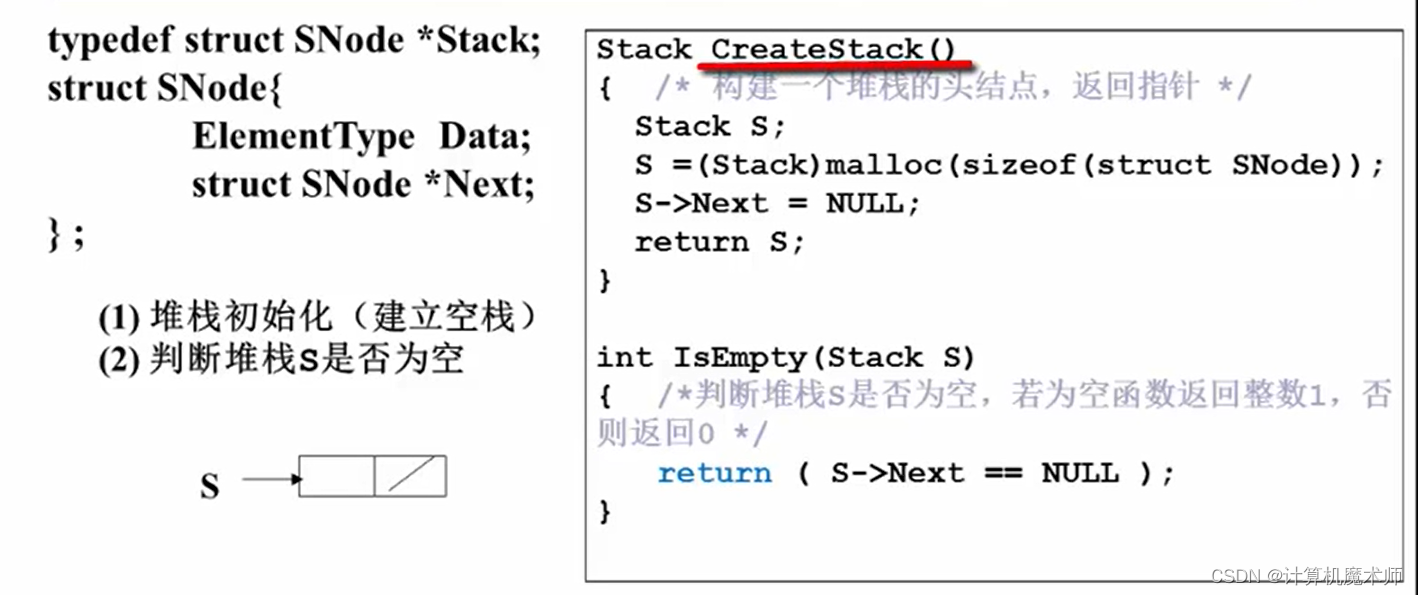
push操作

pop操作

五、表达式求值

回到开头，我们再来 看表达式求值的问题，为了避免运算符中优先级的复杂性，我们使用后缀表达式，并使用堆栈来实现，我们把运算符和运算数丢进堆栈，当为运算符时，pop前两个运算数和运算符运算后再放入栈顶，最后栈顶的运算数便是结果

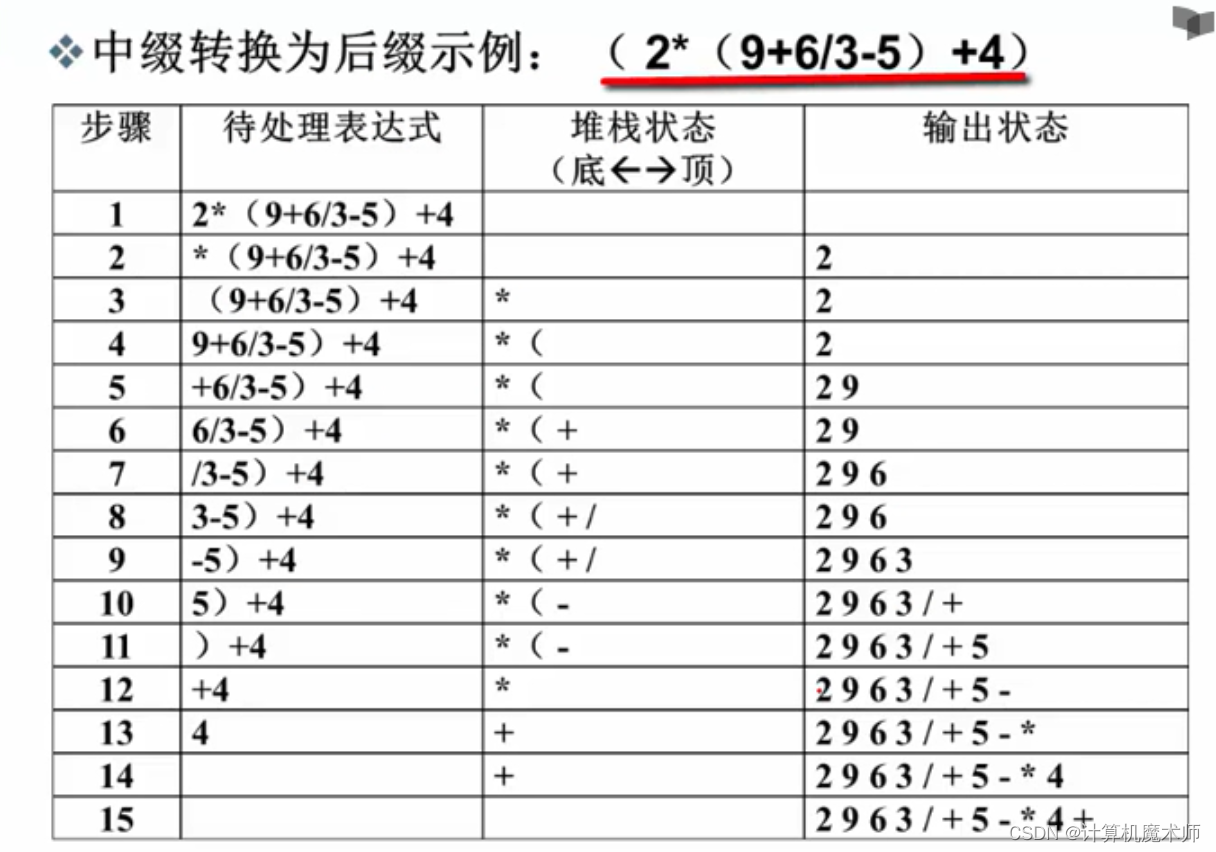
但我们平时所用的都是中缀表达式，所以我们如何把中缀表达式转换成后缀表达式，观察一个例子

其中存储运算符号的结构便是堆栈！那么如果有括号怎么办呢？ 看如下例子

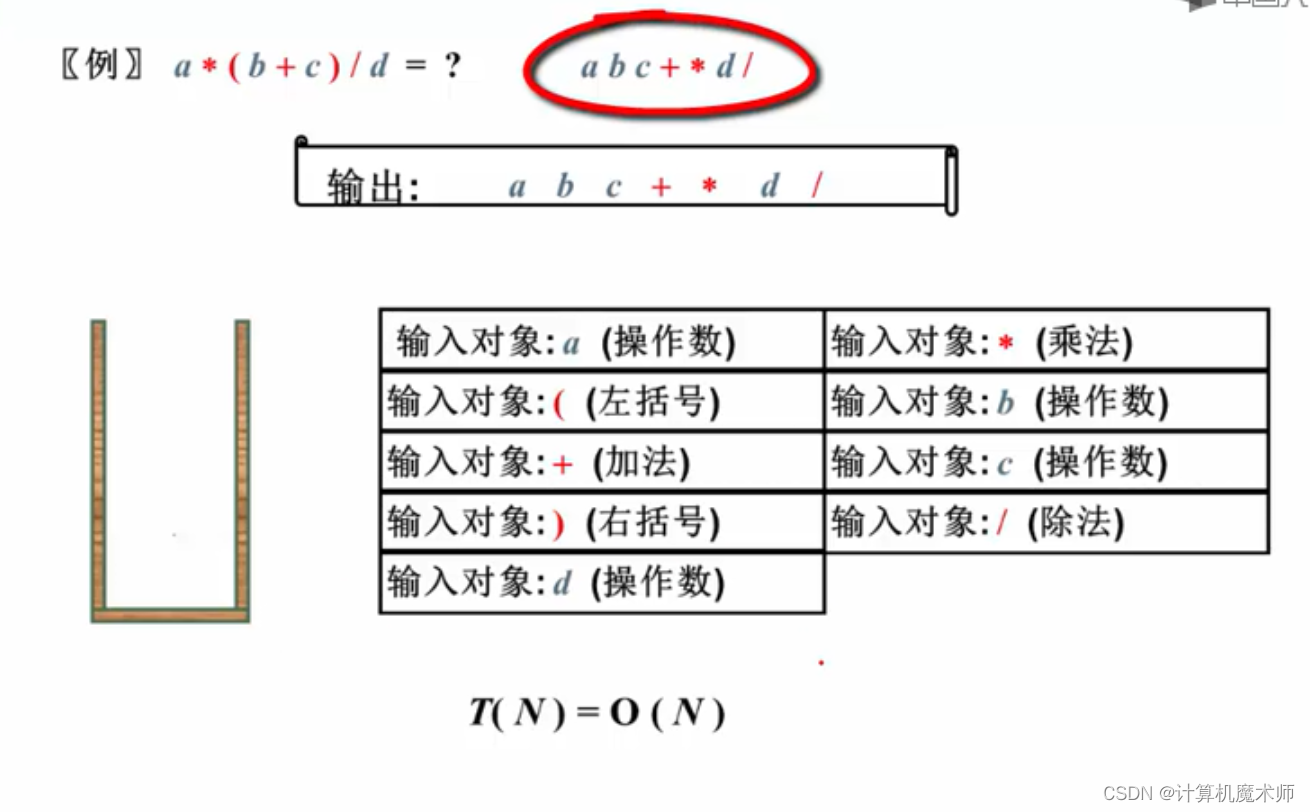
其中运算数保留，遇到左括号时，直到遇到右括号才一直pop栈顶遇到左括号为止，并在括号内做优先级判断，总结如下

小练

除此之外，堆栈还有许多应用

比如函数调用，如果有一系列函数的调用，而我们要保留变量的状态和地址，要实现这些使用堆栈的，且递归函数也是如此，在回溯算法和深度优先搜索（递归）也是如此。

六、队列引入

如上可看到，队列顾名思义，像是平时排队一样，前头服务，后头排队，

七、队列的顺序存储实现

使用数组进行实现

有如下一个例子

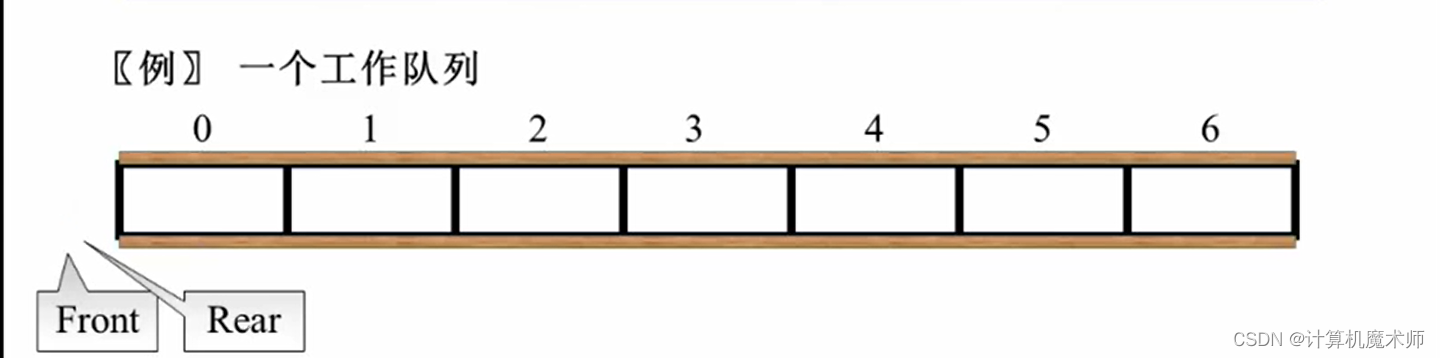
我们以 $-1$ 作为队列为空的标志， 当添加一个工作时，Rear 加一，删除一个工作时，Front加一

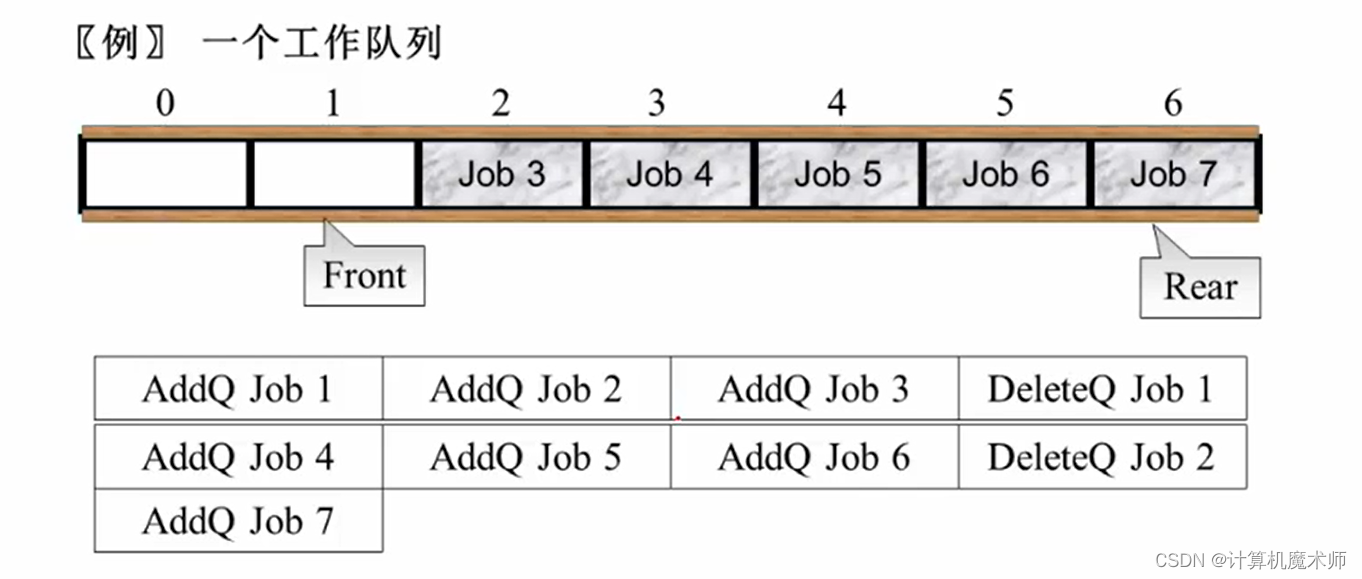
此时队列末尾无法添加了，但实际前面还空着位置，那该如何处理呢？

我们把添加的队列放在Front前面的空位置上，这样就形成循环队列

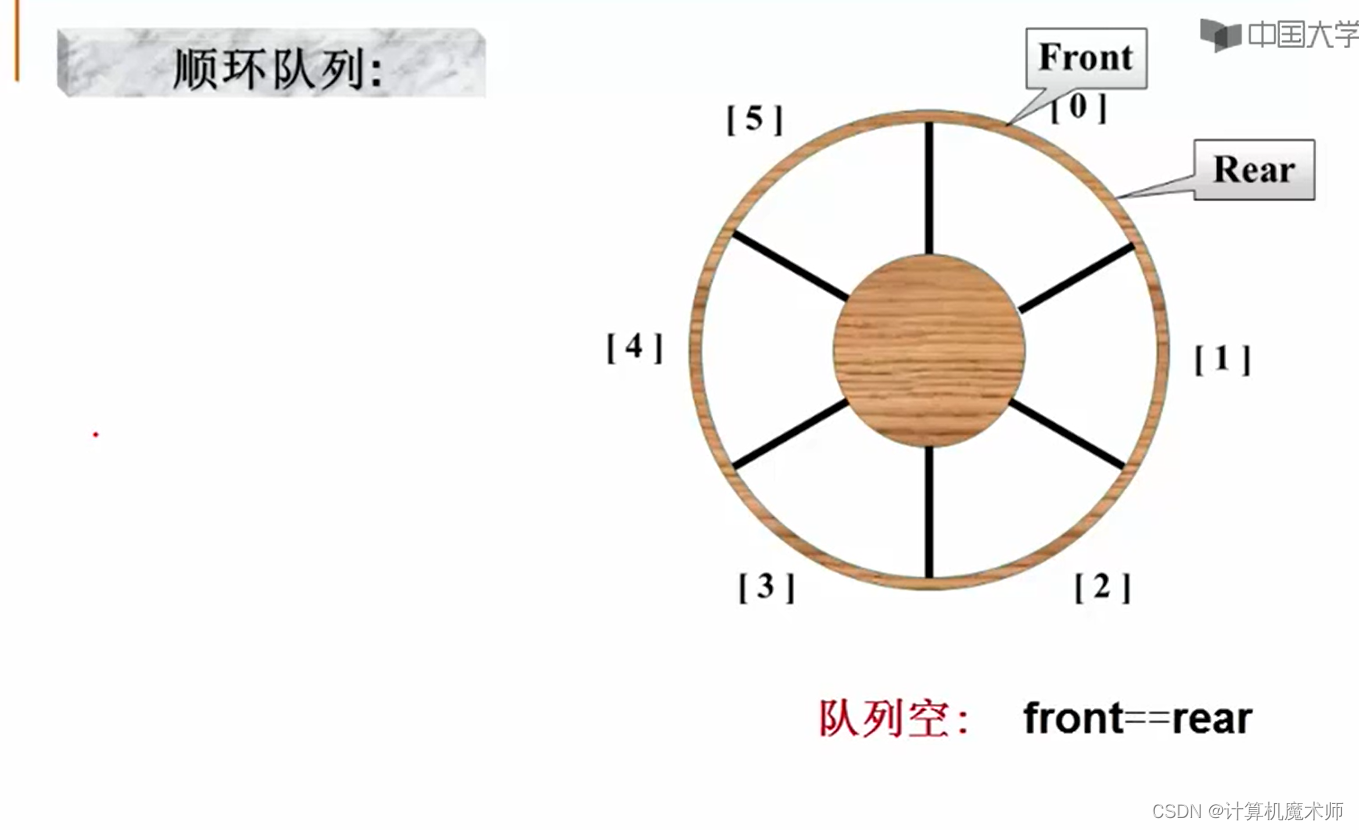
但是这种方式在入队和出队会带来一个问题

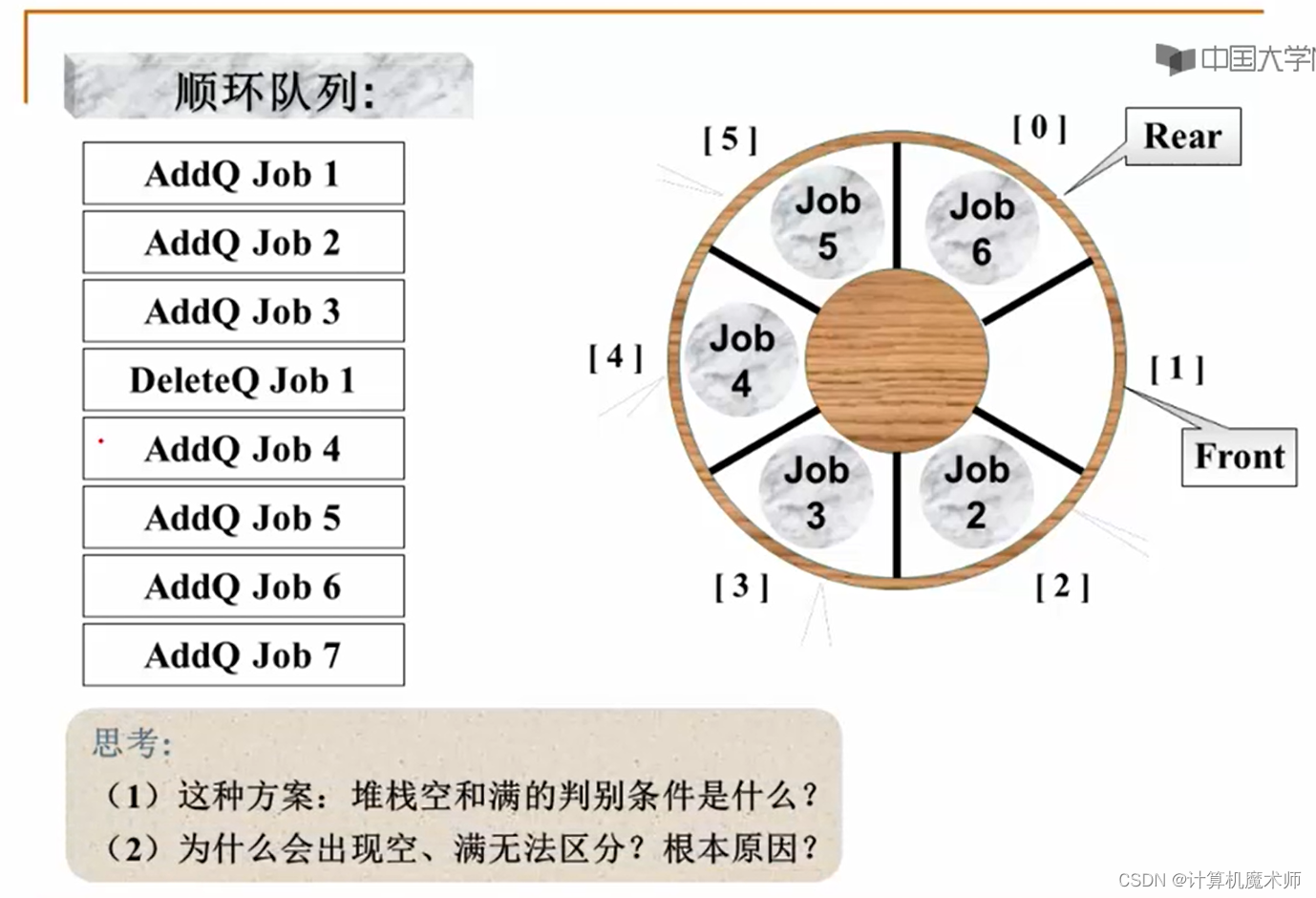
我们观察如下：
数组长度为 n 那么Rear 和 Front 的距离为 0，1，2 ... n-1 总共n种可能，而作为队列装载元素有多少种情况呢？ 有 0,1,2,3,4...n 总共n个装载状态，而装载状态是由 Rear 和 Front 的距离所决定，n种状态无法表达n+1种状态，所以一定会矛盾

解决方法：

1. 使用额外的标记：Size或者tag域
2. 仅使用n-1个数组空间

1）入队列

这里的方法使用了求余方法，使得rear总在 0 ~ MaxSize 中，其中MaxSize是数组长度,当添加一个长度后求余得到结果与队头位置一样，则队列满，

2） 出队列

同样的，首先判断是否为空，不为空，则front往后移动

七、队列的链式存储实现

使用单链表进行实现

对应结构实现，其中队尾的队头指向对应链表首尾

不带头节点的出队操作

当队列只有一个元素，删除时则首位置空，多个元素删除释放空间， 按照这种规则，做入队操作也是如此，添加一个结点，让链表尾指针和rear指向

  ✨谢谢你的阅读，您的点赞和收藏就是我创造的最大动力！✨