文心一言 VS 讯飞星火 VS chatgpt (50)-- 算法导论6.2 2题
二、参考过程 MAX-HEAPIFY,写出能够维护相应最小堆的 MIN-HEAPIFY(A,i)的伪代码,并比较 MIN-HEAPIFY 与 MAX-HEAPIFY 的运行时间。
文心一言:
MIN-HEAPIFY(A, i)的伪代码如下:
1.将节点i及其子树中的最小元素交换到根节点i;
2.对于左子树,递归调用MIN-HEAPIFY(A, 2i);
3.对于右子树,递归调用MIN-HEAPIFY(A, 2i+1);
MAX-HEAPIFY(A, i)的伪代码如下:
1.将节点i及其子树中的最大元素交换到根节点i;
2.对于左子树,递归调用MAX-HEAPIFY(A, 2i);
3.对于右子树,递归调用MAX-HEAPIFY(A, 2i+1);
可以看出,MIN-HEAPIFY和MAX-HEAPIFY的操作非常相似,唯一的区别在于交换的元素不同。因此,它们的运行时间也应该是相似的。
在MIN-HEAPIFY和MAX-HEAPIFY中,每次递归调用都会将问题规模减半,因此它们的运行时间都是O(log n),其中n是数组A的长度。
但是,由于最小堆和最大堆的应用场景不同,它们的操作时间和操作细节也会有所不同。最小堆通常用于优先队列等需要快速找到最小元素的场景,而最大堆则通常用于某些算法中需要快速找到最大元素的场景。

讯飞星火:
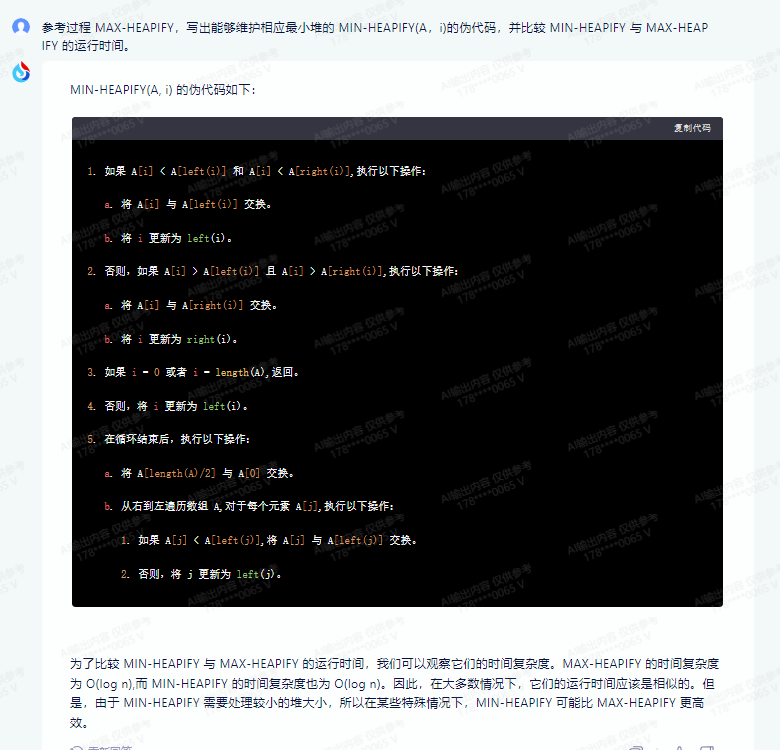
MIN-HEAPIFY(A, i) 的伪代码如下:
1. 如果 A[i] < A[left(i)] 和 A[i] < A[right(i)],执行以下操作:
a. 将 A[i] 与 A[left(i)] 交换。
b. 将 i 更新为 left(i)。
2. 否则,如果 A[i] > A[left(i)] 且 A[i] > A[right(i)],执行以下操作:
a. 将 A[i] 与 A[right(i)] 交换。
b. 将 i 更新为 right(i)。
3. 如果 i = 0 或者 i = length(A),返回。
4. 否则,将 i 更新为 left(i)。
5. 在循环结束后,执行以下操作:
a. 将 A[length(A)/2] 与 A[0] 交换。
b. 从右到左遍历数组 A,对于每个元素 A[j],执行以下操作:
1. 如果 A[j] < A[left(j)],将 A[j] 与 A[left(j)] 交换。
2. 否则,将 j 更新为 left(j)。
为了比较 MIN-HEAPIFY 与 MAX-HEAPIFY 的运行时间,我们可以观察它们的时间复杂度。MAX-HEAPIFY 的时间复杂度为 O(log n),而 MIN-HEAPIFY 的时间复杂度也为 O(log n)。因此,在大多数情况下,它们的运行时间应该是相似的。但是,由于 MIN-HEAPIFY 需要处理较小的堆大小,所以在某些特殊情况下,MIN-HEAPIFY 可能比 MAX-HEAPIFY 更高效。
华为盘古:
360智脑:
伪代码如下所示:
MIN-HEAPIFY(A,i):
if A[i] < A[root]:
swap(A[i], A[root]);
min_index = i;
for j in range(i+1, len(A)):
if A[j] < A[root]:
swap(A[j], A[root]);
min_index = min_index(j);
heapify(A, root, min_index);
其中,heapify(A, root, min_index)是进行最大堆调整的函数。
MAX-HEAPIFY的时间复杂度为 O(log n),而MIN-HEAPIFY的时间复杂度也为O(log n),因此两者的时间复杂度相同。

chatglm:
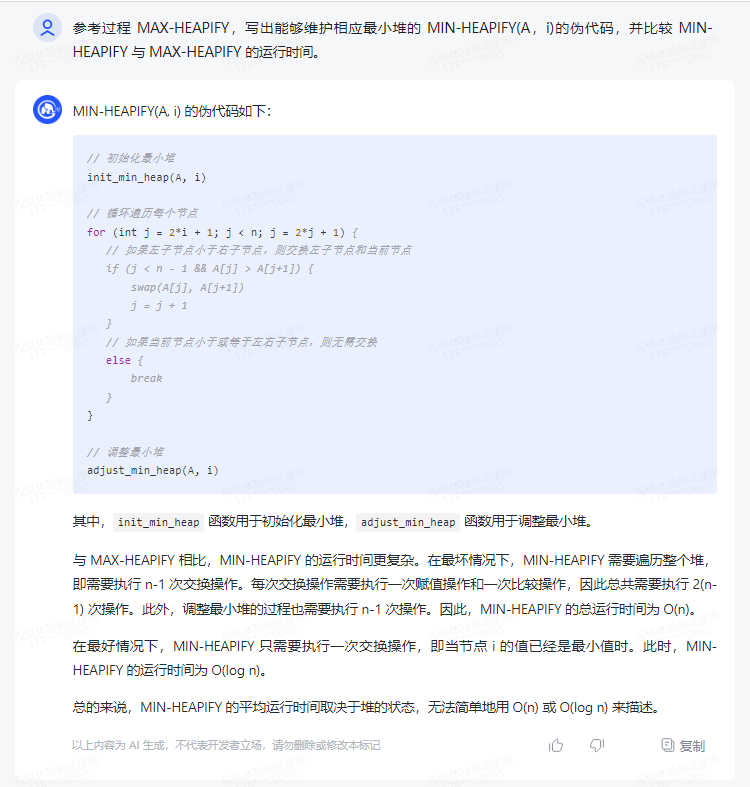
MIN-HEAPIFY(A, i) 的伪代码如下:
// 初始化最小堆
init_min_heap(A, i)
// 循环遍历每个节点
for (int j = 2*i + 1; j < n; j = 2*j + 1) {
// 如果左子节点小于右子节点,则交换左子节点和当前节点
if (j < n - 1 && A[j] > A[j+1]) {
swap(A[j], A[j+1])
j = j + 1
}
// 如果当前节点小于或等于左右子节点,则无需交换
else {
break
}
}
// 调整最小堆
adjust_min_heap(A, i)
其中,init_min_heap 函数用于初始化最小堆,adjust_min_heap 函数用于调整最小堆。
与 MAX-HEAPIFY 相比,MIN-HEAPIFY 的运行时间更复杂。在最坏情况下,MIN-HEAPIFY 需要遍历整个堆,即需要执行 n-1 次交换操作。每次交换操作需要执行一次赋值操作和一次比较操作,因此总共需要执行 2(n-1) 次操作。
此外,调整最小堆的过程也需要执行 n-1 次操作。因此,MIN-HEAPIFY 的总运行时间为 O(n)。
在最好情况下,MIN-HEAPIFY 只需要执行一次交换操作,即当节点 i 的值已经是最小值时。此时,MIN-HEAPIFY 的运行时间为 O(log n)。
总的来说,MIN-HEAPIFY 的平均运行时间取决于堆的状态,无法简单地用 O(n) 或 O(log n) 来描述。
chatgpt:
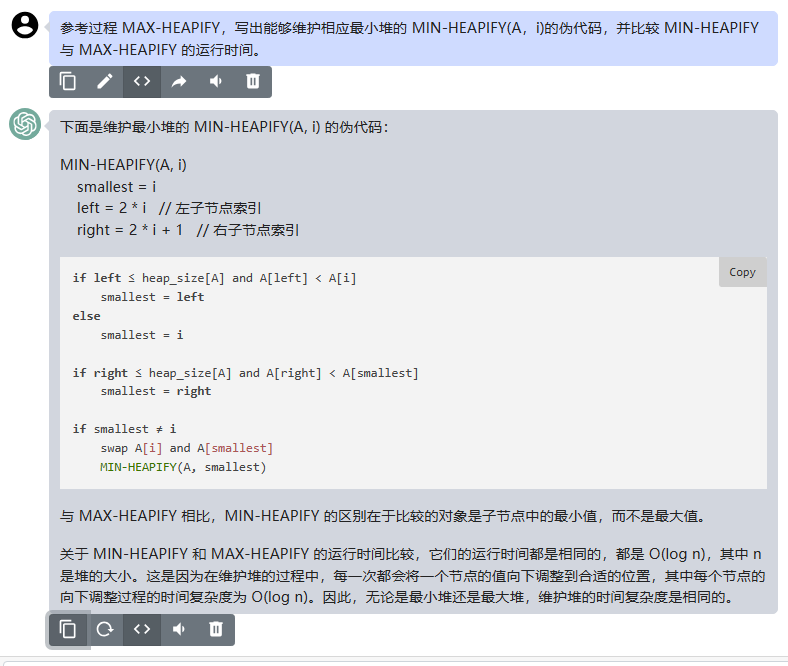
下面是维护最小堆的 MIN-HEAPIFY(A, i) 的伪代码:
MIN-HEAPIFY(A, i)
smallest = i
left = 2 * i // 左子节点索引
right = 2 * i + 1 // 右子节点索引
if left ≤ heap_size[A] and A[left] < A[i]
smallest = left
else
smallest = i
if right ≤ heap_size[A] and A[right] < A[smallest]
smallest = right
if smallest ≠ i
swap A[i] and A[smallest]
MIN-HEAPIFY(A, smallest)
与 MAX-HEAPIFY 相比,MIN-HEAPIFY 的区别在于比较的对象是子节点中的最小值,而不是最大值。
关于 MIN-HEAPIFY 和 MAX-HEAPIFY 的运行时间比较,它们的运行时间都是相同的,都是 O(log n),其中 n 是堆的大小。这是因为在维护堆的过程中,每一次都会将一个节点的值向下调整到合适的位置,其中每个节点的向下调整过程的时间复杂度为 O(log n)。因此,无论是最小堆还是最大堆,维护堆的时间复杂度是相同的。
总结:
void minHeapify(int i) {
int l = left(i);
int r = right(i);
int smallest = i;
if (l <= heapSize && A[l] < A[smallest]) smallest = l;
if (r <= heapSize && A[r] < A[smallest]) smallest = r;
if (smallest != i) {
swap(A[i],A[smallest]);
minHeapify(smallest);
}
}
运行时间相同。
- 点赞
- 收藏
- 关注作者

评论(0)