Latent Diffusion

概述

图像生成是计算机视觉领域的一个重要研究方向，它的目标是根据一些条件（如文本、类别、布局等）来合成逼真的图像。图像生成有很多应用场景，如艺术创作、数据增强、图像修复、图像超分等。

图像生成的方法主要可以分为两大类：基于生成对抗网络（GAN）的方法和基于扩散模型（DM）的方法。GAN是一种利用两个对抗训练的神经网络来生成图像的方法，它可以产生高质量的图像，但也存在一些问题，如训练不稳定、模式崩溃、难以控制等。DM是一种利用一个时序去噪自编码器来生成图像的方法，它可以避免GAN的一些问题，同时也能实现多模态训练和条件生成，但它的缺点是计算代价很高，因为它需要在像素空间上进行多次迭代。

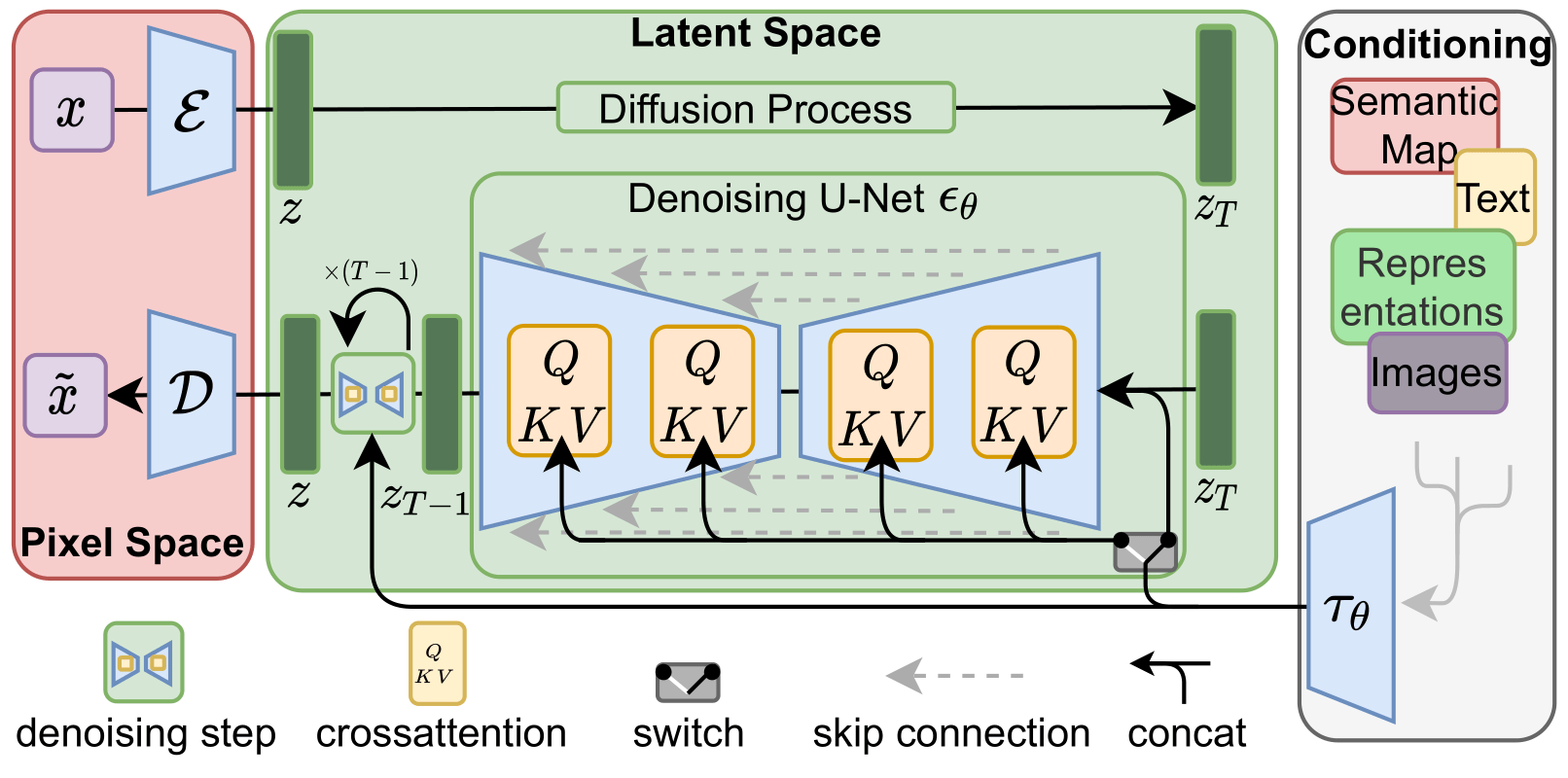
为了解决DM的计算代价问题，潜在扩散模型（Latent Diffusion Models, LDM）提出了一种新的方法。LDM的主要思想是将图像生成过程分解为两个阶段：感知压缩和潜在扩散。感知压缩是指利用一个预训练的自编码器将图像从像素空间压缩到一个低维的潜在表示空间，去除掉高频信息，只保留重要的特征。潜在扩散是指在潜在表示空间上进行扩散操作，通过一个时序去噪自编码器来迭代地“去噪”数据，最后再用自编码器的解码器将潜在表示恢复到原始像素空间。

LDM的优点是可以大幅降低训练和推理阶段的计算复杂度，同时也能达到非常不错的图像生成效果。LDM还引入了交叉注意力机制来实现多模态训练，使得条件图片生成任务也可以实现。LDM在无条件图片生成、图片修复、图片超分等任务上都取得了不错的效果，并且与基于像素的DM相比显著减少了计算资源的需求。

变分编码器

变分编码器(VAE)是一种深度生成模型，可以从数据中学习潜在的特征表示，并用这些特征来生成新的数据。VAE的原理是基于变分贝叶斯推断，利用神经网络来近似真实的后验分布，并最大化数据的边际似然。本文将简要介绍VAE的数学原理和实现方法。

VAE的结构由两个神经网络组成：编码器(encoder)和解码器(decoder)。编码器负责将输入数据 $x$映射到一个潜在空间(latent space)，并输出一个潜在变量 $z$的条件分布 $q(z|x)$，这个分布通常假设为高斯分布，即 $q(z|x)=\mathcal{N}(\mu(x),\Sigma(x))$，其中 $\mu(x)$和 $\Sigma(x)$是编码器的输出。解码器负责根据潜在变量 $z$重构输入数据 $x$，并输出一个重构数据 $x'$的条件分布 $p(x'|z)$，这个分布可以根据数据的类型选择不同的形式，例如对于二值数据可以选择伯努利分布，对于连续数据可以选择高斯分布等。

VAE的目标是最大化输入数据 $x$的边际似然 $p(x)$，即 $p(x)=\int p(x|z)p(z)dz$，其中 $p(z)$是潜在变量 $z$的先验分布，通常假设为标准正态分布，即 $p(z)=\mathcal{N}(0,I)$。然而，由于 $p(x|z)$和 $p(z)$都是非线性函数，直接计算 $p(x)$是非常困难的。因此，VAE采用了一种变分推断(variational inference)的方法，引入了一个近似后验分布 $q(z|x)$来代替真实后验分布 $p(z|x)$，并最小化两者之间的KL散度(Kullback-Leibler divergence)，即

$$\begin{aligned} \text{KL}(q(z|x)||p(z|x))&=\mathbb{E}_{q(z|x)}[\log q(z|x)-\log p(z|x)]\\ &=\mathbb{E}_{q(z|x)}[\log q(z|x)-\log p(x|z)-\log p(z)+\log p(x)]\\ &=\mathbb{E}_{q(z|x)}[\log q(z|x)-\log p(x|z)-\log p(z)]+\log p(x)\\ &=-\mathbb{E}_{q(z|x)}[\log p(x|z)]+\text{KL}(q(z|x)||p(z))+\log p(x) \end{aligned}$$

由于KL散度总是非负的，所以有

$$\begin{aligned} \log p(x)&=\text{KL}(q(z|x)||p(z|x))+\mathbb{E}_{q(z|x)}[\log p(x|z)]-\text{KL}(q(z|x)||p(z))\\ &\geq \mathbb{E}_{q(z|x)}[\log p(x|z)]-\text{KL}(q(z|x)||p(z)) \end{aligned}$$

上式右边被称为证据下界(evidence lower bound, ELBO)，它是 $\log p(x)$的一个下界。因此，最大化 $\log p(x)$等价于最大化ELBO，即

$$\text{ELBO}=\mathbb{E}_{q(z|x)}[\log p(x|z)]-\text{KL}(q(z|x)||p(z))$$

这个目标函数可以通过随机梯度下降法来优化，但是由于 $q(z|x)$是一个不可导的采样过程，所以需要使用一种重参数化(reparameterization)的技巧，即将 $z$表示为一个可导的确定性函数 $g(x,\epsilon)$，其中 $\epsilon$是一个噪声变量，服从标准正态分布。例如，对于高斯分布的 $q(z|x)$，可以令 $g(x,\epsilon)=\mu(x)+\Sigma(x)^{1/2}\epsilon$。这样，ELBO可以写成

$$\text{ELBO}=\mathbb{E}_{\epsilon}[\log p(x|g(x,\epsilon))]-\text{KL}(q(z|x)||p(z))$$

这个目标函数就可以通过反向传播算法来计算梯度，并更新编码器和解码器的参数。

当VAE训练好后，我们可以利用解码器来生成新的数据。具体的过程是从先验分布 $p(z)$中采样一个潜在变量 $z$，然后将其输入解码器得到一个重构数据 $x'$的条件分布 $p(x'|z)$，再从这个分布中采样一个数据 $x'$作为生成数据。

潜在扩散

潜在扩散是LDM的第二个阶段，它主要利用一个时序去噪自编码器来在潜在表示空间上进行扩散操作。扩散操作是指将潜在表示逐渐加入噪声，直到完全变成噪声，然后再逐渐去除噪声，直到恢复成原始潜在表示。这个过程可以看作是一个从数据分布到噪声分布再到数据分布的转换过程，它可以用一个马尔可夫链来描述。扩散操作可以看作是一种随机生成过程，它可以从任意噪声开始，通过反向迭代地去除噪声来生成数据。

扩散操作的实现主要依赖于一个时序去噪自编码器 $\epsilon_\theta\left (z_t, t\right)$ ，它可以用任何深度神经网络来实现，如UNet、Transformer等。论文中使用了一个基于UNet的时序去噪自编码器，并且使用了时间条件（time-conditional）的方法来训练时序去噪自编码器。时间条件是指将时间步t作为一个额外的输入给时序去噪自编码器，从而使得时序去噪自编码器能够根据不同的时间步来调整去噪策略。
给定一个输入图像 x ，我们可以用感知压缩阶段的自编码器将其压缩为一个潜在表示 $z_0=\mathcal {E} (x)$ ，然后用扩散操作将其转换为一个噪声 $z_T$ 。扩散操作可以用以下公式来描述：

$$z_t=\sqrt {1-\beta_t} z_{t-1} + \sqrt {\beta_t} \epsilon_t$$

这里， $t=1,2,...,T$ 是时间步， $T$是扩散操作的总步数， $\beta_t$ 是噪声方差的系数， $\epsilon_t \sim \mathcal {N} (0, I)$ 是一个标准正态分布的噪声。可以看出，当 $t=0$ 时， $z_0=z_0$，即原始潜在表示；当 $t=T$ 时， $z_T \sim \mathcal {N} (0, I)$，即完全的噪声。因此，扩散操作可以看作是一个从 $z_0$ 到 $z_T$ 的转换过程。

反过来，我们也可以用扩散操作将噪声 $z_T$ 转换为潜在表示 $z_0$ ，然后用感知压缩阶段的自编码器将其解压为一个图像 $x$ 。这个过程可以用以下公式来描述：

$$z_{t-1}=\frac {1}{\sqrt {1-\beta_t}} \left (z_t - \sqrt {\beta_t} \epsilon_\theta\left (z_t, t\right) \right)$$

这里， $t=T,T-1,...,1$ 是时间步， $T$ 是扩散操作的总步数， $\beta_t$ 是噪声方差的系数， $\epsilon_\theta\left (z_t, t\right)$ 是时序去噪自编码器的输出。可以看出，当 $t=T$ 时， $z_T=z_T$ ，即任意的噪声；当 t=0 时， $z_0=z_0$ ，即原始潜在表示。因此，扩散操作可以看作是一个从 $z_T$ 到 $z_0$ 的转换过程。

潜在扩散的好处是可以实现高效和灵活的图像生成。高效是指潜在扩散只需要在低维的潜在表示空间上进行操作，而不需要在高维的像素空间上进行操作，从而大大降低了计算复杂度和内存消耗。灵活是指潜在扩散可以从任意噪声开始生成图像，而不需要依赖于特定的数据分布或先验分布，从而增加了生成多样性和可控性。

潜在扩散的实现主要依赖于一个时序去噪自编码器 $\epsilon_\theta\left (z_t, t\right)$，它可以用任何深度神经网络来实现，如UNet、Transformer等。论文中使用了一个基于UNet的时序去噪自编码器，并且使用了时间条件（time-conditional）的方法来训练时序去噪自编码器。时间条件是指将时间步t作为一个额外的输入给时序去噪自编码器，从而使得时序去噪自编码器能够根据不同的时间步来调整去噪策略。

交叉注意力

交叉注意力机制是一种用于实现多模态训练和条件图片生成的技术，它可以使得diffusion模型能够根据不同的输入条件来调整生成图像的内容和风格。交叉注意力机制的原理是利用一个注意力模块来计算不同模态之间的相关性和重要性，从而使得生成图像能够符合给定的条件。比如，如果输入条件是一段文本，那么交叉注意力机制可以使得生成图像能够包含文本中提到的物体、颜色、动作等信息；如果输入条件是一张图像，那么交叉注意力机制可以使得生成图像能够保留图像中的风景、人物、氛围等特征。

交叉注意力机制的实现主要依赖于一个交叉注意力模块 $\mathcal {A}$，它可以用任何深度神经网络来实现，如Transformer等。论文1中使用了一个基于Transformer的交叉注意力模块，并且使用了自注意力（self-attention）和互注意力（cross-attention）的方法来训练交叉注意力模块。自注意力是指在同一模态内部应用注意力机制，从而使得输入能够捕捉自身的结构和语义。互注意力是指在不同模态之间应用注意力机制，从而使得输入能够捕捉不同模态之间的关联和对齐。

给定一个输入图像 x 和一个输入文本 y ，我们可以用感知压缩阶段的自编码器将图像压缩为一个潜在表示 $z_0=\mathcal {E}(x)$，然后用交叉注意力模块将文本编码为一个潜在表示 $w=\mathcal {A}(y)$ ，然后用互注意力机制将两个潜在表示融合为一个潜在表示 $z’_0=\mathcal {A} (z_0, w)$ ，然后用扩散操作将其转换为一个噪声 $z_{T}$，然后再反向扩散操作将其转换为一个潜在表示 $z’_0$，然后再用感知压缩阶段的自编码器将其解压为一个图像 $x’$ 。这个过程可以用以下公式来描述：

$$z’_0=\mathcal {A} (z_0, w) z_T=\sqrt {1-\beta_T} z’_{T-1} + \sqrt {\beta_T} \epsilon_T z’_{t-1}=\frac {1}{\sqrt {1-\beta_t}} \left (z’t - \sqrt {\beta_t} \epsilon\theta\left (z’_t, t, w\right) \right) x’=\mathcal {D} (z’_0)$$

这里，t=T,T-1,…,1 是时间步，T 是扩散操作的总步数，w 是文本的潜在表示，z’_0 是融合后的潜在表示，x’ 是生成的图像。

生成效果示例