“AI Earth”人工智能创新挑战赛：助力精准气象和海洋预测Baseline[2]：数据探索性分析（温度风场可视化）、CNN+LSTM模型建模

1.气象海洋预测-数据分析

数据分析是解决一个数据挖掘任务的重要一环，通过数据分析，我们可以了解标签的分布、数据中存在的缺失值和异常值、特征与标签之间的相关性、特征之间的相关性等，并根据数据分析的结果，指导我们后续的特征工程以及模型的选择和设计。

在本次任务中，将探索赛题中给出的两份训练数据，可视化分析四个气象特征的分布情况，思考如何进行特征工程以及如何选择或设计模型来实现我们的预测任务。

• 学习目标
  1. 学习如何探索并可视化分析气象数据。
  2. 根据数据分析结果思考以下两个问题：
     • 能否构造新的特征？
     • 选择或设计什么样的模型进行预测？

本赛题使用的训练数据包括CMIP5中17个模式提供的140年的历史模拟数据、CMIP6中15个模式提供的151年的历史模拟数据和美国SODA模式重建的100年的历史观测同化数据，采用nc格式保存，其中CMIP5和CMIP6分别是世界气候研究计划(WCRP)的第5次和第6次耦合模式比较计划，这二者都提供了多种不同的气候模式对于多种气候变量的模拟数据。这些数据包含四种气候变量：海表温度异常(SST)、热含量异常(T300)、纬向风异常(Ua)、经向风异常(Va)，数据维度为(year, month, lat, lon)，对于训练数据提供对应月份的Nino3.4指数标签数据。简而言之，提供的训练数据中的每个样本为某年、某月、某个维度、某个经度的SST、T300、Ua、Va数值，标签为对应年、对应月的Nino3.4指数。

需要注意的是，样本的第二维度month的长度不是12个月，而是36个月，对应从当前year开始连续三年的数据，例如SODA训练数据中year为0时包含的是从第1 - 第3年逐月的历史观测数据，year为1时包含的是从第2年 - 第4年逐月的历史观测数据，也就是说，样本在时间上是有交叉的。

另外一点需要注意的是，Nino3.4指数是Nino3.4区域从当前月开始连续三个月的SST平均值，也就是说，我们也可以不直接预测Nino3.4指数，而是以SST为预测目标，间接求得Nino3.4指数。测试数据为国际多个海洋资料同化结果提供的随机抽取的 $N$段长度为12个月的时间序列，数据采用npy格式保存，维度为(12, lat, lon, 4)，第一维度为连续的12个月份，第四维度为4个气候变量，按SST、T300、Ua、Va的顺序存放。测试集文件序列的命名如test_00001_01_12.npy中00001表示编号，01表示起始月份，12表示终止月份。

在本次任务中我们需要用到global_land_mask这个Python库，这个库可以根据输入的纬度和经度判断该点是否在陆地上。

项目链接以及码源见文末

# !unzip -d input /home/aistudio/data/data221707/enso_round1_train_20210201.zip

# 安装global_land_mask
!pip install global_land_mask

import numpy as np
import matplotlib.pyplot as plt
import random
import netCDF4
import seaborn as sns
from global_land_mask import globe
from scipy import interpolate
plt.rcParams['font.sans-serif'] = ['SimHei'] #中文支持
%matplotlib inline

1.1 以SODA数据集为例，探索标签的分布情况

# 读取SODA数据

# 存放数据的路径
path = '/home/aistudio/'
data = netCDF4.Dataset(path + 'SODA_train.nc')
label = netCDF4.Dataset(path + 'SODA_label.nc')
label = np.array(label.variables['nino'])

print(data.variables['sst'].shape)

(100, 36, 24, 72)

label.shape

(100, 36)

可以看到，数据集中的每个样本是以某一年为起始的接下来36个月的气象数据，同样的，标签也是以这一年为起始的接下来36个月中每个月的Nino3.4指数。然而一年只有12个月，怎么会有36个月的数据呢？

我们不妨来查看一下，将每个样本中的12个月进行拼接时，Nino3.4指数的变化曲线。

# 分别将样本中的0-12月、12-24月、24-36月进行拼接，绘制Nino3.4指数的变化曲线
plt.figure(figsize=(8, 10))
plt.subplots_adjust(hspace=0.4, wspace=0.4)
for i in range(3):
    label_all = [label[j, 12*i:12*(i+1)] for j in range(label.shape[0])]
    label_all = np.concatenate(label_all, axis=0)
    plt.subplot(3, 1, i+1)
    plt.plot(label_all, 'k', linewidth=1)
    plt.xlabel('Time / month')
    plt.ylabel('Nino')
    plt.title('nino: month{}-{}'.format(12*i, 12*(i+1)))
plt.show()

/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/matplotlib/font_manager.py:1331: UserWarning: findfont: Font family ['sans-serif'] not found. Falling back to DejaVu Sans
  (prop.get_family(), self.defaultFamily[fontext]))

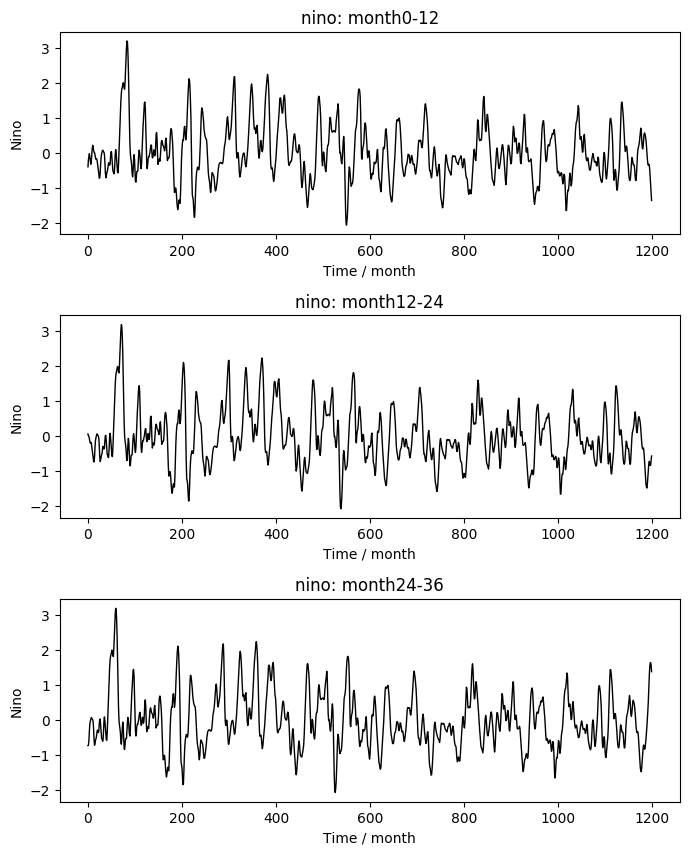
从图中可以看出，三条曲线的变化趋势是完全相同的，只是在时间上有12个月的位移。这说明，重叠部分的标签是相同的，给出这样的样本的目的是可以以前12个月作为模型的输入X、后24个月为预测目标Y构建训练样本。

进一步思考，将每个样本构建一个训练样本，那么我们所能得到的训练数据量就只有4645（CMIP数据）+100（SODA数据）=4745条，这样小的数据量用于模型训练必然是不够的，那么如何增加数据量呢？这个问题留待大家思考。

同样的，我们可以随机抽取三个样本，查看每个样本中的Nino3.4指数变化曲线。

# 随机抽取三个样本，绘制Nino3.4指数变化曲线
plt.figure(figsize=(8, 10))
plt.subplots_adjust(hspace=0.4, wspace=0.4)
for i in range(3):
    y = random.randint(0, label.shape[0])
    plt.subplot(3, 1, i+1)
    plt.plot(label[y], 'k', linewidth=1)
    plt.xlabel('Time / month')
    plt.ylabel('Nino')
    plt.title('nino: year{}'.format(y))
plt.show()

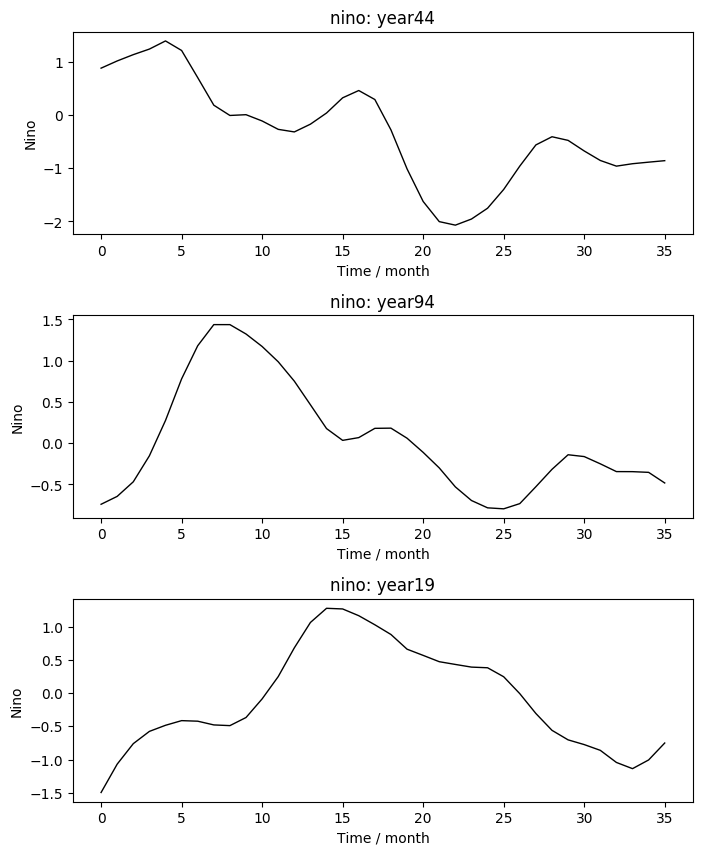
1.2 以SST特征为例，进行海陆掩膜和插值分析

在给定数据中，经度和纬度坐标都是离散的，每隔5度有一个坐标点，在这样的经纬度坐标下的SST值也是离散的，因此我们以样本0第0月的SST数据为例，用插值函数来拟合经纬度坐标与SST值之间的函数关系，得到平滑的SST分布。

lon = np.array(data.variables['lon'])
lat = np.array(data.variables['lat'])

x = lon
y = lat
# 以纬度和经度生成网格点坐标矩阵
xx, yy = np.meshgrid(x, y)
# 取样本0第0月的SST值
z = data.variables['sst'][0, 0]
# 采用三次多项式插值，得到z = f(x, y)的函数f
f = interpolate.interp2d(x, y, z, kind = 'cubic')

x

array([  0.,   5.,  10.,  15.,  20.,  25.,  30.,  35.,  40.,  45.,  50.,
        55.,  60.,  65.,  70.,  75.,  80.,  85.,  90.,  95., 100., 105.,
       110., 115., 120., 125., 130., 135., 140., 145., 150., 155., 160.,
       165., 170., 175., 180., 185., 190., 195., 200., 205., 210., 215.,
       220., 225., 230., 235., 240., 245., 250., 255., 260., 265., 270.,
       275., 280., 285., 290., 295., 300., 305., 310., 315., 320., 325.,
       330., 335., 340., 345., 350., 355.])

经度的实际取值是从-180°到0°到180°，而给定的数据中经度的取值是0°到360度每间隔5°取一个坐标值，因此在之后判断是否为陆地时需要转换为实际的经度。

y

array([-55., -50., -45., -40., -35., -30., -25., -20., -15., -10.,  -5.,
         0.,   5.,  10.,  15.,  20.,  25.,  30.,  35.,  40.,  45.,  50.,
        55.,  60.])

数据中纬度的取值也是每间隔5°取一个坐标值。判断每个经纬度坐标点是否在陆地上，用空值遮盖陆地部分，便于观察海洋上SST的分布。

# 将经度x转换为实际经度重新生成网格点坐标矩阵
lon_grid, lat_grid = np.meshgrid(x-180, y)
# 判断坐标矩阵上的网格点是否为陆地
is_on_land = globe.is_land(lat_grid, lon_grid)
is_on_land = np.concatenate([is_on_land[:, x >= 180], is_on_land[:, x < 180]], axis=1)
# 进行陆地掩膜，将陆地的SST设为空值
z[is_on_land] = np.nan
# 可视化掩膜结果，黄色为陆地，紫色为海洋
plt.imshow(is_on_land[::-1, :])

<matplotlib.image.AxesImage at 0x7f5d009a5950>

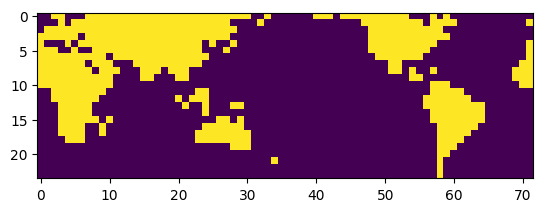
z.shape

(24, 72)

# 可视化海洋上的SST分布
plt.imshow(z[::-1, :], cmap=plt.cm.RdBu_r)

<matplotlib.image.AxesImage at 0x7f5d0090c390>

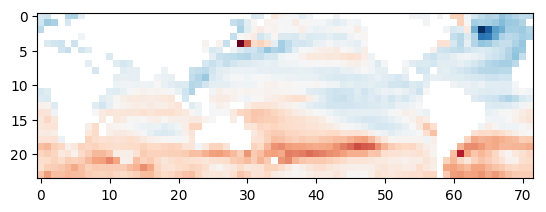
由上图可以看到，SST的分布是离散的，我们用之前得到的插值函数来平滑SST值，可视化平滑后的SST分布。

# 设置间隔为1°的经纬度坐标网格，用插值函数得到该坐标网格点的SST值
xnew = np.arange(0, 356, 1)
ynew = np.arange(-65, 66, 1)
znew = f(xnew, ynew)
lon_grid, lat_grid = np.meshgrid(xnew-180, ynew)
is_on_land = globe.is_land(lat_grid, lon_grid)
is_on_land = np.concatenate([is_on_land[:, xnew >= 180], is_on_land[:, xnew < 180]], axis=1)
# 同样进行陆地掩膜
znew[is_on_land] = np.nan
# 绘制平滑后的SST分布图
plt.imshow(znew[::-1, :], cmap=plt.cm.RdBu_r)

<matplotlib.image.AxesImage at 0x7f5d008efd50>

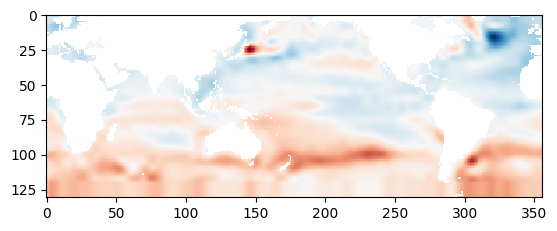
我们用同样的方法绘制样本0中每个月的SST分布图，观察SST分布的变化。

# 绘制0年36个月的海陆掩膜
for i in range(1):
    plt.figure(figsize=(15, 18))
    for j in range(36):
        x = lon
        y = lat
        xx, yy = np.meshgrid(x, y)
        z = data.variables['sst'][i, j]
        f = interpolate.interp2d(x, y, z, kind='cubic')
        
        xnew = np.arange(0, 356, 1)
        ynew = np.arange(-65, 66, 1)
        znew = f(xnew, ynew)
        
        lon_grid, lat_grid = np.meshgrid(xnew-180, ynew)
        is_on_land = globe.is_land(lat_grid, lon_grid)
        is_on_land = np.concatenate([is_on_land[:, xnew >= 180], is_on_land[:, xnew < 180]], axis=1)
        znew[is_on_land] = np.nan
        plt.subplot(9, 4, j+1)
        plt.imshow(znew[::-1, :], cmap=plt.cm.RdBu_r)
        plt.title('sst - year:{}, month:{}'.format(i+1, j+1))

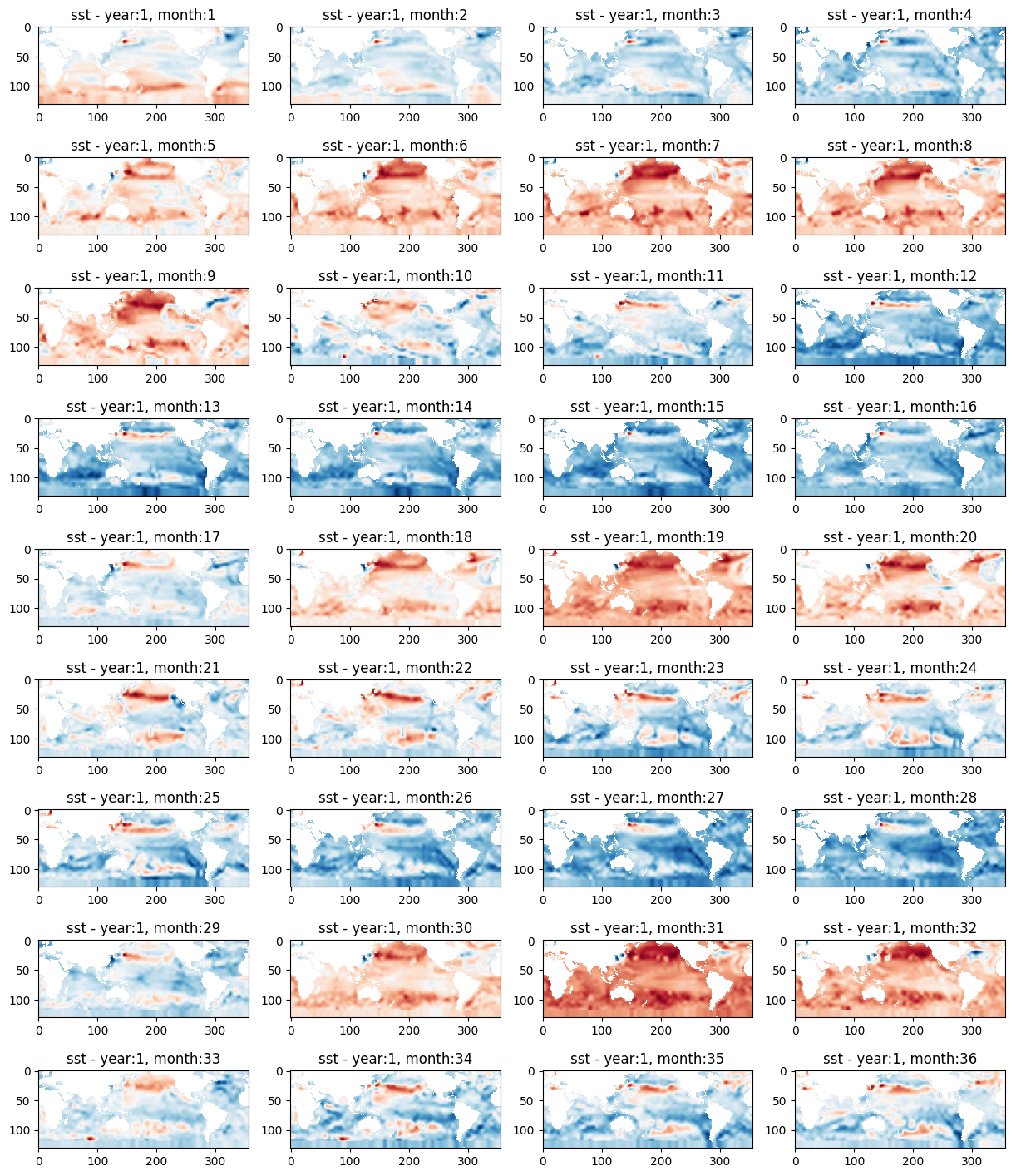
可以看到，SST在每12个月中的前4个月和后4个月都较低，在中间4个月时较高，这说明，海表温度在春季和冬季较低，在夏季和秋季呈现逐渐升高到最高点然后逐渐降低的变化趋势，这与我们的认知常识是相符的。

大家也可以用同样的方法观察分析其它三个气象特征的变化趋势。

1.3以CMIP数据集为例，进行缺失值分析

# 读取CMIP数据

# 存放数据的路径
path = '/home/aistudio/input/enso_round1_train_20210201/'
data = netCDF4.Dataset(path + 'CMIP_train.nc')
label = netCDF4.Dataset(path + 'CMIP_label.nc')
label = np.array(label.variables['nino'])

# 获得陆地的掩膜
lon_grid, lat_grid = np.meshgrid(x-180, y)
is_on_land = globe.is_land(lat_grid, lon_grid)
is_on_land = np.concatenate([is_on_land[:, x >= 180], is_on_land[:, x < 180]], axis=1)
mask = np.zeros(data.variables['sst'].shape, dtype=int)
mask[:, :, :, :] = is_on_land[np.newaxis, np.newaxis, :, :]

# 查看SST特征的缺失值数量
name = 'sst'
data_ = np.array(data.variables[name])
before_nan = np.sum(np.isnan(data_))
print('before:', before_nan)

before: 0

# 查看T300特征的缺失值数量
name = 't300'
data_ = np.array(data.variables[name])
before_nan = np.sum(np.isnan(data_))
print('before:', before_nan)

before: 3055032

# 查看Va特征的缺失值数量
name = 'va'
data_ = np.array(data.variables[name])
before_nan = np.sum(np.isnan(data_))
print('before:', before_nan)

before: 13921123

# 查看Ua特征的缺失值数量
name = 'ua'
data_ = np.array(data.variables[name])
before_nan = np.sum(np.isnan(data_))
print('before:', before_nan)

before: 13921123

四个气象特征中，SST特征不存在缺失值，Va和Ua特征中的缺失值数量最多。

接下来以Ua特征为例，可视化分析缺失值的情况。

# 统计每年每月中Ua特征的缺失值数量
m = np.zeros(data_.shape[0:2])
for i in range(data_.shape[0]):
    for j in range(data_.shape[1]):
        if np.sum(np.isnan(data_[i][j])) != 0:
            m[i, j] = np.sum(np.isnan(data_[i, j]))

# 计算每一年的缺失值
before = np.sum(m, axis=1)
# 可视化每一年的缺失值数量
plt.plot(before, 'k')
plt.ylabel('nan count')
plt.xlabel('year')
plt.show()

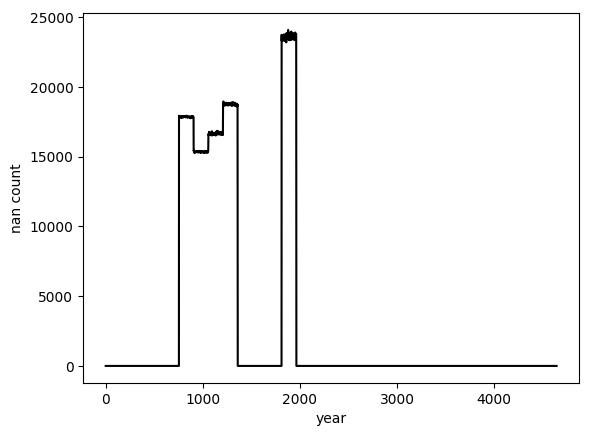
可以看到在某些年份中存在较多缺失值。

# 查看Ua特征中存在缺失值的年数
len(np.where(before!=0)[0])

755

我们取样本1900来观察Ua特征的分布。

# 可视化样本1900中Ua特征的分布
plt.imshow(data_[1900, 0][::-1, :])

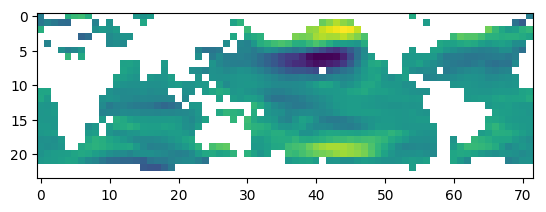
上图中白色部分即为缺失值，可以看到，缺失值多数分布在陆地上，我们将陆地部分进行填充，观察填充后Ua的分布。

# 将陆地位置填0
data_[mask==1] = 0

# 可视化填充后样本1900中Ua特征的分布
plt.imshow(data_[1900, 0][::-1, :])

<matplotlib.image.AxesImage at 0x7f5c18dc4d10>

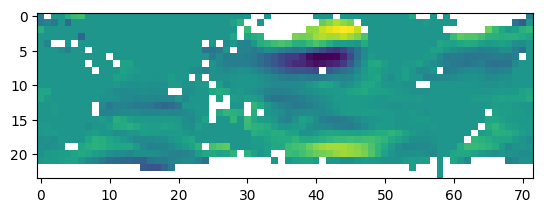
对陆地部分进行填充后缺失值数量大大减少。

# 统计填充后缺失值的数量
after_nan = np.sum(np.isnan(data_))

print('before: %d \nafter: %d \npercentage: %f'%(before_nan, after_nan, 1 - float(after_nan) / before_nan))

before: 13921123 
after: 2440742 
percentage: 0.824673

陆地部分填充处理了82%的缺失值。

# 可视化填充后每一年的缺失值数量
m = np.zeros(data_.shape[0: 2])
for i in range(data_.shape[0]):
    for j in range(data_.shape[1]):
        if np.sum(np.isnan(data_[i, j])) != 0:
            m[i, j] = np.sum(np.isnan(data_[i, j]))
after = np.sum(m, axis=1)
plt.plot(after, 'k')
plt.ylabel('nan count')
plt.xlabel('year')
plt.show()

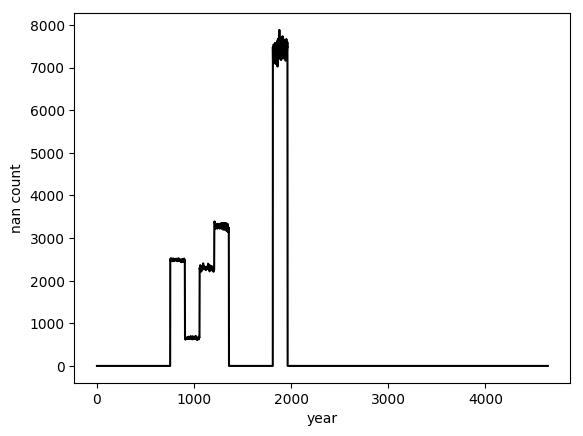
# 对比填充前后每一年缺失值的数量
plt.plot(before, 'k')
plt.plot(after, 'r')
plt.legend(['before', 'after'])
plt.title(name)
plt.ylabel('nan count')
plt.xlabel('year')
plt.show()

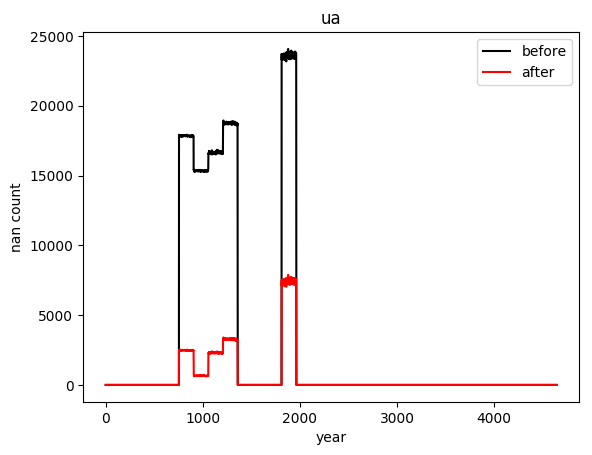
1.4温度场和风场可视化

在气候问题中，温度与风向往往是密切相关的。当温度越高时，气压越低，空气向上流动，温度越低时，气压越高，空气向下流动，于是温度高的地方上方的空气就会向温度低的地方流动，形成风。因此在分析气候问题时，我们往往会把温度和风向放在一起进行可视化。

如何把风向可视化呢？这里我们要用到plt.quiver()这个函数。

plt.quiver()用于绘制二维的向量场，主要输入参数有：

• X：向量起始点的X轴坐标
• Y：向量起始点的Y轴坐标
• U：向量的X轴分量
• V：向量的Y轴分量

# 对温度场SST进行插值，得到插值函数
x = lon
y = lat
xx, yy = np.meshgrid(x, y)
z = data.variables['sst'][0, 0]
f = interpolate.interp2d(x, y, z, kind='cubic')

# 获得陆地掩膜
lon_grid, lat_grid = np.meshgrid(x-180, y)
is_on_land = globe.is_land(lat_grid, lon_grid)
is_on_land = np.concatenate([is_on_land[:,x>=180], is_on_land[:,x<180]], axis=1)

# 对Ua和Va进行陆地掩膜
ua = data.variables['ua'][0, 0]
ua[is_on_land] = np.nan
va = data.variables['va'][0, 0]
va[is_on_land] = np.nan

# 插值后生成平滑的SST分布
xnew = np.arange(0, 356, 1)
ynew = np.arange(-65, 66, 1)
znew = f(xnew, ynew)

# 对平滑后的SST进行陆地掩膜
lon_grid, lat_grid = np.meshgrid(xnew-180, ynew)
is_on_land = globe.is_land(lat_grid, lon_grid)
is_on_land = np.concatenate([is_on_land[:, xnew >= 180], is_on_land[:, xnew < 180]], axis=1)
znew[is_on_land] = np.nan

# 绘制温度场
plt.figure(figsize=(15, 10))
plt.imshow(znew[::-1, :], cmap=plt.cm.RdBu_r)
plt.colorbar(orientation='horizontal') # 显示水平颜色条
# 绘制风向场，其实这里准确来说绘制的是风向异常的向量，而非实际的风向
plt.quiver(lon, lat+65, ua[::-1, :], va[::-1, :], alpha=0.8) # 在坐标(lon, lat)处绘制与sqrt(ua^2, va^2)成正比长度的箭头
plt.title('year0-month0: SST/UA-VA')
plt.show()

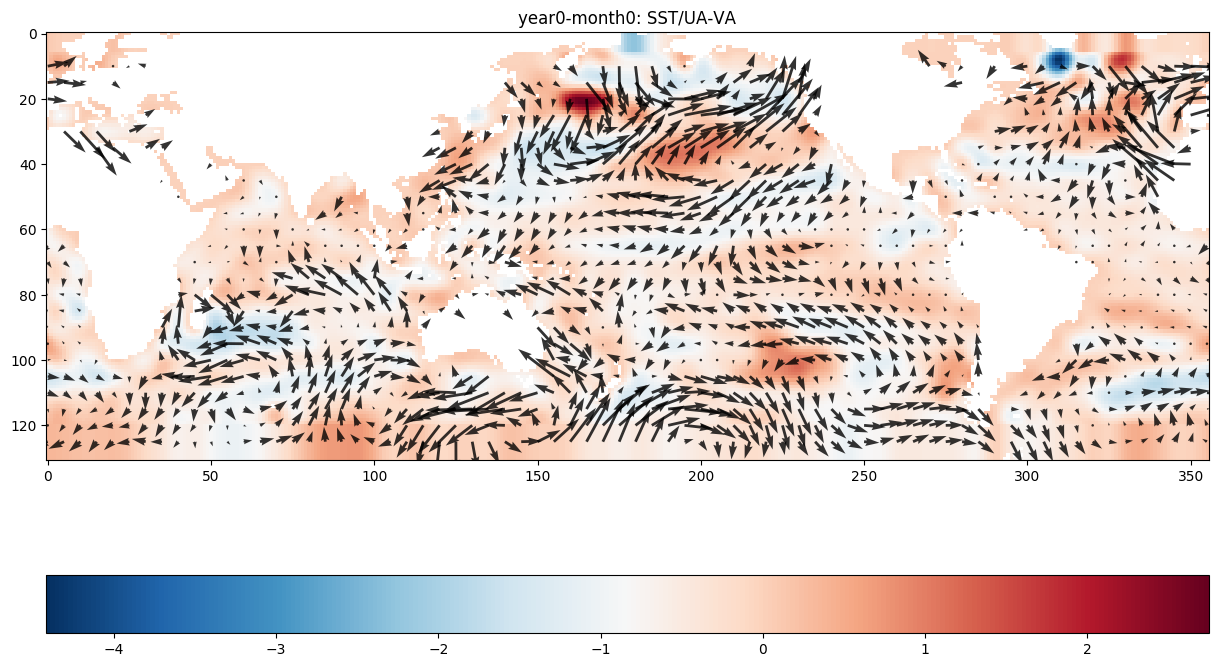
从上图中可以看出，温度异常SST在0值附近时没有明显的风向异常，而在其他区域风向异常通常由SST值大的地方指向SST值小的地方。

ENSO现象是指在温度场上赤道东太平洋温度持续异常增暖，在风向场上热带东太平洋与热带西太平洋气压变化（表现为风向）相反的现象。在上图这个样本中没有出现ENSO现象，大家可以用同样的方法绘制并观察存在ENSO现象（Nino3.4指数连续5个月超过0.5℃）的样本的温度和风场。

1.5 小结

在以上的数据分析中，不难看出我们在分析气象问题时，采用的仍然是通用的数据分析思路：分析标签 -> 分析特征（包括特征分布、特征与特征的关系、特征与标签的关系） -> 分析数据的基本情况（包括缺失值、异常值、重复值等）。这个思路大家可以灵活应用到各种问题的分析中去，不至于拿到数据后无从下手。

通过以上的数据分析，我们可以得到以下结论：

1. 重叠部分的标签是相同的，为了增加数据量，我们可以从每条数据中取固定的12个月拼接起来，用滑窗构建训练数据集。
2. SST特征中没有缺失值，在其他特征中，缺失值基本上在陆地部分，将陆地部分用0填充可以解决绝大部分的缺失值。

现在我们回到开篇的学习目标中提出的第一个问题：能否构造新的特征？目前的答案是不能。从各位TOP选手的方案以及相关的ENSO预测的论文来看，大家的目光都聚焦在如何构建模型上，而鲜少有人会去构造新的特征。这与其说是不能，更不如说是不必要，因为一般我们构造新的特征是为了从给出的特征中得到与预测目标更相关的特征，由此提高模型的学习效果，但是就本赛题而言，构造统计特征或者其他新的特征收效不高，我们更希望通过模型来挖掘给定数据之间在时间和空间上的依赖关系。

于是，解题的重点就落到了第二个问题上：选择或设计什么样的模型进行预测？在接下来的三个任务中，我们就要来学习TOP选手们的建模方案。

2.气象海洋预测-模型建立之CNN+LSTM

本次任务我们将学习来自TOP选手“学习AI的打工人”的建模方案，该方案中采用的模型是CNN+LSTM。

在本赛题中，我们构造的模型需要完成两个任务，挖掘空间信息以及挖掘时间信息。那么，说到挖掘空间信息的模型，我们会很自然的想到CNN，同样的，挖掘时间信息的模型我们会很容易想到LSTM，我们本次学习的这个TOP方案正是构造了CNN+LSTM的串行结构。

2.1 数据处理

该TOP方案的数据处理主要包括四部分：

1. 增加月特征。将序列数据的起始月份作为新的特征。
2. 数据扁平化。将序列数据按月拼接起来通过滑窗增加数据量。
3. 空值填充。
4. 构造数据集。随机采样构造数据集。

# 读取数据
# 存放数据的路径
path = '/kaggle/input/ninoprediction/'
soda_train = nc.Dataset(path + 'SODA_train.nc')
soda_label = nc.Dataset(path + 'SODA_label.nc')
cmip_train = nc.Dataset(path + 'CMIP_train.nc')
cmip_label = nc.Dataset(path + 'CMIP_label.nc')

2.1.2 增加月特征

本赛题的线上测试集是任意选取某个月为起始的长度为12的序列，因此该方案中增加了起始月份作为新的特征。但是使用整数1~12不能反映12月与1月相邻这一特点，因此需要借助三角函数的周期性，同时考虑到单独使用sin函数或cos函数会存在某些月份的函数值相同的现象，因此同时使用sin函数和cos函数作为两个新增月份特征，保证每个起始月份的这两个特征组合都是独一无二的，并且又能够很好地表现出月份的周期性特征。

我们可以通过可视化直观地感受下每个月份所构造的月份特征组合。

months = range(0, 12)
month_labels = ['Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun', 'Jul', 'Aug', 'Sept', 'Oct', 'Nov', 'Dec']
# sin月份特征
months_sin = map(lambda x: math.sin(2 * math.pi * x / len(months)), months)
# cos月份特征
months_cos = map(lambda x: math.cos(2 * math.pi * x / len(months)), months)

# 绘制每个月的月份特征组合
plt.figure(figsize=(20, 5))
x_axis = np.arange(-1, 13, 1e-2)
sns.lineplot(x=x_axis, y=np.sin(2 * math.pi * x_axis / len(months)))
sns.lineplot(x=x_axis, y=np.cos(2 * math.pi * x_axis / len(months)))
sns.scatterplot(x=months, y=months_sin, s=200)
sns.scatterplot(x=months, y=months_cos, s=200)
plt.xticks(ticks=months, labels=month_labels)
plt.show()

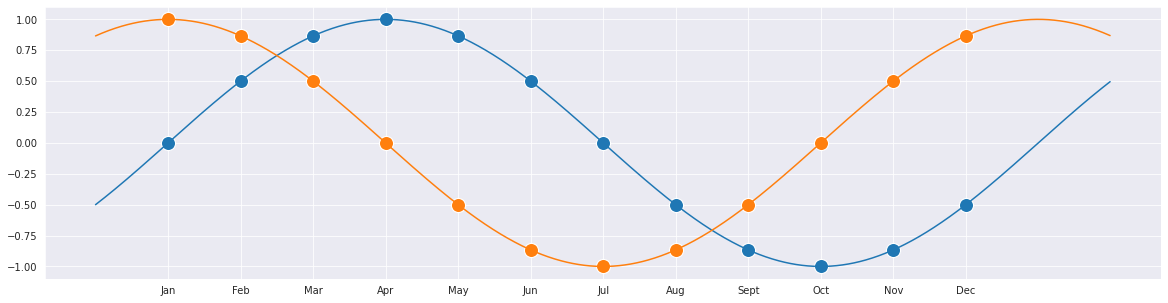
构造SODA数据的sin月份特征。

# 构造一个维度为100*36*24*72的矩阵，矩阵中的每个值为所在月份的sin函数值
soda_month_sin = np.zeros((100, 36, 24, 72))
for y in range(100):
    for m in range(36):
        for lat in range(24):
            for lon in range(72):
                soda_month_sin[y, m, lat, lon] = math.sin(2 * math.pi * (m % 12) / 12)
                
soda_month_sin.shape

(100, 36, 24, 72)

构造SODA数据的cos月份特征。

# 构造一个维度为100*36*24*72的矩阵，矩阵中的每个值为所在月份的cos函数值
soda_month_cos = np.zeros((100, 36, 24, 72))
for y in range(100):
    for m in range(36):
        for lat in range(24):
            for lon in range(72):
                soda_month_cos[y, m, lat, lon] = math.cos(2 * math.pi * (m % 12) / 12)
                
soda_month_cos.shape

(100, 36, 24, 72)

构造CMIP数据的sin月份特征。

# 构造一个维度为4645*36*24*72的矩阵，矩阵中的每个值为所在月份的sin函数值
cmip_month_sin = np.zeros((4645, 36, 24, 72))
for y in range(4645):
    for m in range(36):
        for lat in range(24):
            for lon in range(72):
                cmip_month_sin[y, m, lat, lon] = math.sin(2 * math.pi * (m % 12) / 12)
                
cmip_month_sin.shape

(4645, 36, 24, 72)

构造CMIP数据的cos月份特征。

# 构造一个维度为4645*36*24*72的矩阵，矩阵中的每个值为所在月份的cos函数值
cmip_month_cos = np.zeros((4645, 36, 24, 72))
for y in range(4645):
    for m in range(36):
        for lat in range(24):
            for lon in range(72):
                cmip_month_cos[y, m, lat, lon] = math.cos(2 * math.pi * (m % 12) / 12)
                
cmip_month_cos.shape

(4645, 36, 24, 72)

2.1.2 数据扁平化

在Task2中我们发现，赛题中给出的数据量非常少，如何增加数据量呢？对于时序数据，一种常用的做法就是滑窗。

由于每条数据在时间上有重叠，我们取数据的前12个月拼接起来，就得到了长度为（数据条数×12个月）的序列数据，如图1所示：

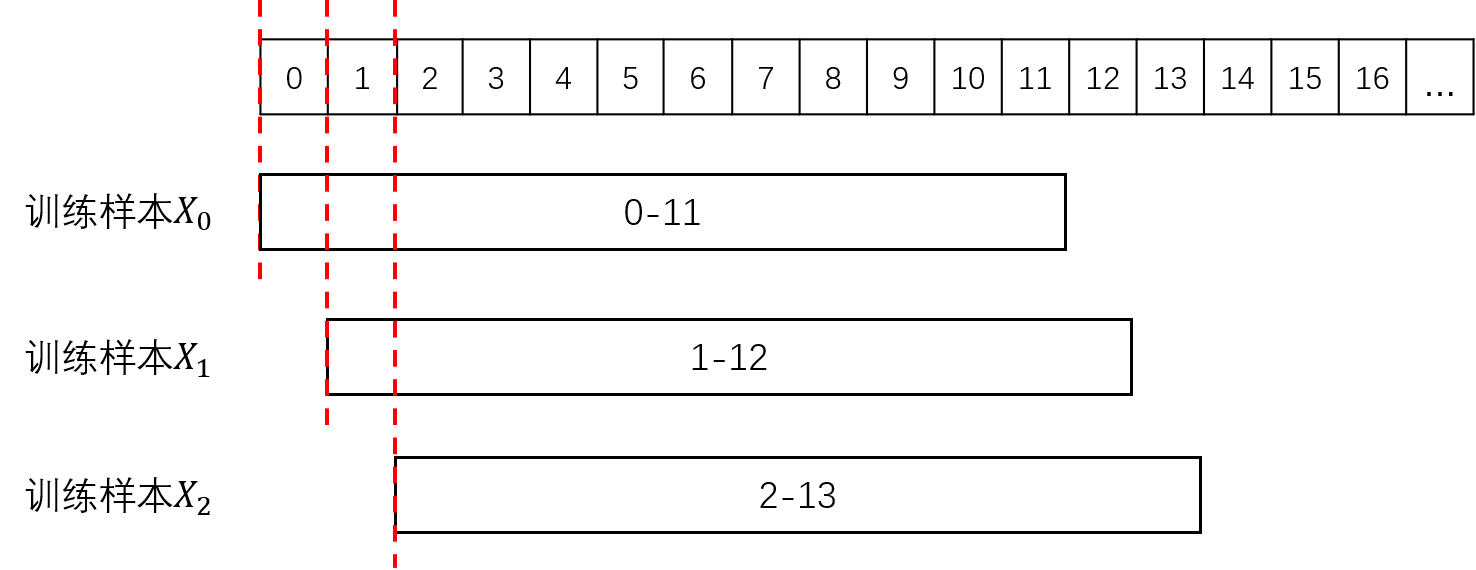
然后我们以每个月为起始月，接下来的12个月作为模型输入X，后24个月的Nino3.4指数作为预测目标Y构建训练样本，如图2所示：

需要注意的是，CMIP数据提供了不同的拟合模式，只有在同种模式下各个年份的数据在时间上是连续的，因此同种模式的数据才能在时间上拼接起来，除去最后11个月不能构成训练样本外，滑窗最终能获得的训练样本数量可以按以下方式计算得到：

• SODA：1种模式×（100年×12-11）=1189条样本
• CMIP6：15种模式×（151年×12-11）=27015条样本
• CMIP5：17种模式×（140年×12-11）=28373条样本

在下面的代码中，我们只将各个模式的数据拼接起来而没有采用滑窗，这是因为考虑到采用滑窗得到的训练样本维度是（数据条数×12×24×72），需要占用大量的内存资源。我们在之后构建数据集时，随机抽取了部分样本，大家在实际问题中，如果资源足够的话，可以采用滑窗构建的全部的数据，不过需要注意数据量大的情况下可以考虑构建更深的模型来挖掘更多信息。

2.1.3 空值填充

在Task2中我们发现，除SST外，其它特征中都存在空值，这些空值基本都在陆地上，因此我们直接将空值填充为0。

2.2 构造数据集

在划分训练/验证集时，一个需要考虑的问题是训练集、验证集、测试集三者的分布是否是一致的。在本赛题中我们拿到的是两份数据，其中CMIP数据是CMIP5/6模式模拟的历史数据，SODA数据是由SODA模式重建的的历史观测同化数据，线上测试集则是来自国际多个海洋资料的同化数据，由此看来，SODA数据和线上测试集的分布是较为一致的，CMIP数据的分布则与测试集不同。在三者不一致的情况下，我们通常会尽可能使验证集与测试集的分布一致，这样当模型在验证集上有较好的表现时，在测试集上也会有较好的表现。

因此，我们从CMIP数据的每个模式中各抽取100条数据作为训练集（这里抽取的样本数只是作为一个示例，实际模型训练的时候使用多少样本需要综合考虑可用的资源条件和构建的模型深度），从SODA模式中抽取100条数据作为验证集。有的同学可能会疑惑，既然这里只用了100条SODA数据，那么为什么还要对SODA数据扁平化后再抽样而不直接用原始数据呢，因为直接取原始数据的前12个月作为输入，后24个月作为标签所得到的验证集每一条都是从0月开始的，而线上的测试集起始月份是随机抽取的，因此这里仍然要尽可能保证验证集与测试集的数据分布一致，使构建的验证集的起始月份也是随机的。

我们这里没有构造测试集，因为线上的测试集已经公开了，可以直接使用，在比赛时，线上的测试集是保密的，需要构造线下的测试集来评估模型效果，同时需要注意线下的评估结果和线上的提交结果是否差距不大或者变化趋势是一致的，如果不是就需要调整线下的测试集，保证它和线上测试集的分布尽可能一致，能够较为准确地指示模型的调整方向。

2.3 模型构建

在模型构建部分的通用流程是：构造评估函数 -> 构建并训练模型 -> 模型评估，后两步是循环的，可以根据评估结果重新调整并训练模型，再重新进行评估。

2.3.1构造评估函数

模型的评估函数通常就是官方给出的评估指标，不过在比赛中经常会出现线下的评估结果和提交后的线上评估结果不一致的情况，这通常是线下测试集和线上测试集分布不一致造成的。

2.3.2模型构造与训练

这部分是赛题的重点，该TOP方案采用的是CNN+LSTM的串行结构，其中CNN用来提取空间信息，LSTM用来提取时间信息，模型结构如下图所示。

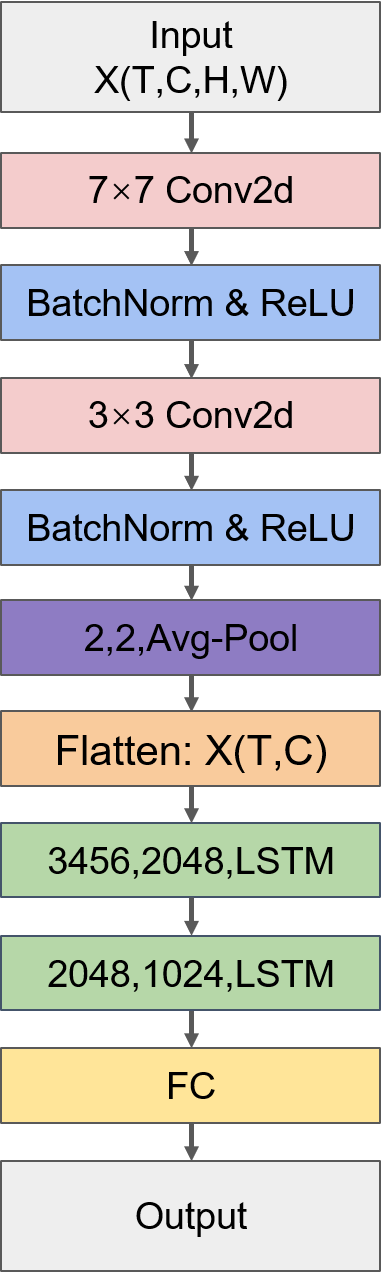
• CNN部分

CNN常用于处理图像信息，它在处理空间信息上也有很好的表现。CNN的输入尺寸是（N,C,H,W），其中N是批量梯度下降中一个批次的样本数量，H和W分别是输入图像的高和宽，C是输入图像的通道数，对于本题中的空间数据，H和W就对应数据的纬度和经度，C对应特征数。我们的训练样本中还多了一个时间维度，因此需要用将输入数据的格式(N,T,H,W,C)转换为(N×T,C,H,W)。

BatchNormalization（后面简称BN）是批标准化层，通常放在卷积层后用于标准化数据的分布，能够减少各层不同数据分布之间的相互影响和依赖，具有加快模型训练速度、避免梯度爆炸、在一定程度上能增强模型泛化能力等优点，是神经网络问题中常用的“大杀器”。不过目前关于BN层和ReLU激活函数的放置顺序孰先孰后的问题众说纷纭，具体还是看模型的效果。关于这个问题的讨论可以参考https://www.zhihu.com/question/283715823

总体来看CNN这一部分采用的是比较通用的结构，第一层采用比较大的卷积核（7×7），后面接多层的小卷积核（3×3），并用BN提升模型效果，用池化层减少模型参数、扩大感受野，池化层常用的有MaxPooling和AveragePooling，通常MaxPooling效果更好，不过具体看模型效果。模型的主要难点就在于调参，目前模型调参没有标准的答案，更多地是参考前人的经验以及不断地尝试。

• LSTM部分

CNN部分经过Flatten层将除时间维度以外的维度压平（即除时间步长12外的其它维度大小相乘，例如CNN部分最后的池化层输出维度是（N,T,C,H,W），则压平后的维度是（N,T,C×H×W）），输入LSTM层。LSTM层接受的输入维度为（Time_steps，Input_size），其中Time_steps就是时间步长12，Input_size是压平后的维度大小。Pytorch中LSTM的主要参数是input_size、hidden_size（隐层节点数）、batch_first（一个批次的样本数量N是否在第1维度），batch_first为True时输入和输出的数据格式为(N,T,input_size/hidden_size)，为数据格式为(T,N,input_size/hidden_size)，需要注意的一点是LSTM的输出形式是tensor格式的output和tuple格式的(h_n,c_n)，其中output是所有时间步的输出(N,T,hidden_size)，h_n是隐层的输出（即最后一个时间步的输出，格式为(1,N,hidden_size)），c_n是记忆细胞cell的输出。因为我们通过多层LSTM要获得的并非一个时间序列，而是要抽取出一个关于输入序列的特征表达，因此最后我们使用最后一个LSTM层的隐层输出h_n作为全连接层的输入。LSTM的使用方法可以参考https://pytorch.org/docs/stable/generated/torch.nn.LSTM.html?highlight=lstm#torch.nn.LSTM

由于LSTM有四个门，因此LSTM的参数量是4倍的Input_size×hidden_size，参数量过多就容易过拟合，同时由于数据量也较少，因此该方案中只堆叠了两个LSTM层。

考虑到本次任务的评价指标score=2/3×accskill-RMSE，其中RMSE是24个月的rmse的累计值，我们这里可以自定义评价指标中的RMSE作为损失函数。

# 采用RMSE作为损失函数
def RMSELoss(y_pred,y_true):
    loss = torch.sqrt(torch.mean((y_pred-y_true)**2, dim=0)).sum()
    return loss

model_weights = './task03_model_weights.pth'
device = 'cuda' if torch.cuda.is_available() else 'cpu'
model = Model().to(device)
criterion = RMSELoss
optimizer = optim.Adam(model.parameters(), lr=1e-3, weight_decay=0.001)  # weight_decay是L2正则化参数
epochs = 10
train_losses, valid_losses = [], []
scores = []
best_score = float('-inf')
preds = np.zeros((len(y_valid),24))

for epoch in range(epochs):
    print('Epoch: {}/{}'.format(epoch+1, epochs))
    
    # 模型训练
    model.train()
    losses = 0
    for data, labels in tqdm(trainloader):
        data = data.to(device)
        labels = labels.to(device)
        optimizer.zero_grad()
        pred = model(data)
        loss = criterion(pred, labels)
        losses += loss.cpu().detach().numpy()
        loss.backward()
        optimizer.step()
    train_loss = losses / len(trainloader)
    train_losses.append(train_loss)
    print('Training Loss: {:.3f}'.format(train_loss))
    
    # 模型验证
    model.eval()
    losses = 0
    with torch.no_grad():
        for i, data in tqdm(enumerate(validloader)):
            data, labels = data
            data = data.to(device)
            labels = labels.to(device)
            pred = model(data)
            loss = criterion(pred, labels)
            losses += loss.cpu().detach().numpy()
            preds[i*batch_size:(i+1)*batch_size] = pred.detach().cpu().numpy()
    valid_loss = losses / len(validloader)
    valid_losses.append(valid_loss)
    print('Validation Loss: {:.3f}'.format(valid_loss))
    s = score(y_valid, preds)
    scores.append(s)
    print('Score: {:.3f}'.format(s))
    
    # 保存最佳模型权重
    if s > best_score:
        best_score = s
        checkpoint = {'best_score': s,
                      'state_dict': model.state_dict()}
        torch.save(checkpoint, model_weights)

# 绘制训练/验证曲线
def training_vis(train_losses, valid_losses):
    # 绘制损失函数曲线
    fig = plt.figure(figsize=(8,4))
    # subplot loss
    ax1 = fig.add_subplot(121)
    ax1.plot(train_losses, label='train_loss')
    ax1.plot(valid_losses,label='val_loss')
    ax1.set_xlabel('Epochs')
    ax1.set_ylabel('Loss')
    ax1.set_title('Loss on Training and Validation Data')
    ax1.legend()
    plt.tight_layout()

training_vis(train_losses, valid_losses)

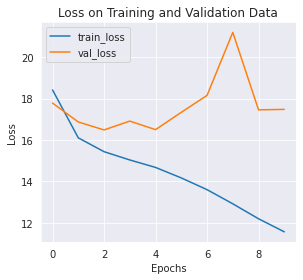
我们通常会绘制训练/验证曲线来观察模型的拟合情况，上图中我们分别绘制了训练过程中训练集和验证集损失函数变化曲线。可以看到，训练集的损失函数下降很快，但是验证集的损失函数是震荡的，没有明显的下降，这说明模型的学习效果较差，并存在过拟合问题，需要调整相关的参数。

2.3.3模型评估

最后，我们在测试集上评估模型的训练结果。

# 加载最佳模型权重
checkpoint = torch.load('../input/ai-earth-model-weights/task03_model_weights.pth')
model = Model()
model.load_state_dict(checkpoint['state_dict'])

<All keys matched successfully>

# 测试集路径
test_path = '../input/ai-earth-tests/'
# 测试集标签路径
test_label_path = '../input/ai-earth-tests-labels/'

import os

# 读取测试数据和测试数据的标签，并记录每个测试样本的起始月份用于之后构造月份特征
files = os.listdir(test_path)
X_test = []
y_test = []
first_months = []  # 样本起始月份
for file in files:
    X_test.append(np.load(test_path + file))
    y_test.append(np.load(test_label_path + file))
    first_months.append(int(file.split('_')[2]))

X_test = np.array(X_test)
y_test = np.array(y_test)
X_test.shape, y_test.shape

((103, 12, 24, 72, 4), (103, 24))

# 构造一个维度为103*12*24*72的矩阵，矩阵中的每个值为所在月份的sin函数值
test_month_sin = np.zeros((103, 12, 24, 72, 1))
for y in range(103):
    for m in range(12):
        for lat in range(24):
            for lon in range(72):
                test_month_sin[y, m, lat, lon] = math.sin(2 * math.pi * ((m + first_months[y]-1) % 12) / 12)
                
test_month_sin.shape

(103, 12, 24, 72, 1)

# 构造一个维度为103*12*24*72的矩阵，矩阵中的每个值为所在月份的cos函数值
test_month_cos = np.zeros((103, 12, 24, 72, 1))
for y in range(103):
    for m in range(12):
        for lat in range(24):
            for lon in range(72):
                test_month_cos[y, m, lat, lon] = math.cos(2 * math.pi * ((m + first_months[y]-1) % 12) / 12)
                
test_month_cos.shape

(103, 12, 24, 72, 1)

# 构造测试集
X_test = np.concatenate([X_test, test_month_sin, test_month_cos], axis=-1)
X_test.shape

(103, 12, 24, 72, 6)

testset = AIEarthDataset(X_test, y_test)
testloader = DataLoader(testset, batch_size=batch_size, shuffle=False)

# 在测试集上评估模型效果
model.eval()
model.to(device)
preds = np.zeros((len(y_test),24))
for i, data in tqdm(enumerate(testloader)):
    data, labels = data
    data = data.to(device)
    labels = labels.to(device)
    pred = model(data)
    preds[i*batch_size:(i+1)*batch_size] = pred.detach().cpu().numpy()
s = score(y_test, preds)
print('Score: {:.3f}'.format(s))

4it [00:00, 65.03it/s]

Score: 14.946

2.4 总结

• 该方案在数据处理部分采用了滑窗来构造数据集，这是序列预测问题中常用的增加数据量的方法。另外，该方案中增加了一组月份特征，个人认为在时序场景中增加的这组特征收益不高，更多的是通过模型挖掘序列中的依赖关系，并且由于维度增加会使得训练数据占用的资源大大增加，对模型的效果提升不明显。不过在其他场景中这种特征构造方法仍然是值得借鉴的。

• 该方案没有选择时空序列预测领域的现有模型，而是选择自己设计模型，方案中的这种构造模型的思路非常适合初学者学习，灵活地将不同模型串行或并行组合能够结合模型各自的优势，这种模型构造方法需要注意的是一个模型的输出维度与另一个模型接受的输入维度要相互匹配。

• 尝试在不增加月份特征的情况下使用CNN+LSTM模型进行预测，同时尝试修改模型参数或层数比较模型在测试集上的评分。

• 未能解决的问题

正如其他参赛者一样，我们碰到最大的问题就是成绩波动问题。即使什么都不变，只是随机数的变化都会使得线上成绩有非常大的变化(10分上下都是可能的)。 我们尝试了许多手段，可能最容易想到的就是SODA和其他两个模式应该不在一个域上，所以需要通过迁移学习或者域自适应来解决这个问题。但是尝试均以失败告终。

• 其他尝试
  • 增加模型层数(对于该问题，层数越多貌似效果越不好)
  • 修改模型中的卷积层，池化层等
  • 更换损失函数和优化器
  • 将SST,T300,Ua,Va分成4通道分别输入模型
  • 只使用SST的特征作为模型的输入
  • 使用域自适应做成一个双输出的模型：1个正常的输出，另一个输出用来区分SODA，CMIP6还是CMIP5。
  • 尝试自注意力机制
  • 收集几个线上分数比较好的模型，然后融合

项目链接以及码源见文末

链接跳转到文末，欢迎订阅

更多文章请关注公重号：汀丶人工智能