二叉树的顺序结构——堆的概念&&实现（图文详解+完整源码 | C语言版）

举报
花想云 发表于 2023/05/31 23:51:02 2023/05/31
【摘要】 堆的概念及实现

​

 ​编辑


目录

0.写在前面

1.什么是堆？

2.堆的实现

2.1 堆的结构定义

2.2 函数声明

2.3 函数实现

2.3.1 AdjustUp（向上调整算法）

2.3.2 AdjustDown（向下调整算法）

2.3.3 HeapCreate（如何建堆）

2.3.4 建堆的时间复杂度

3. 完整源码

Heap.h文件

Heap.c文件 

Test.c文件 

0.写在前面

上一章中介绍了树和二叉树的概念及结构，本章我们将学习堆的实现。其中涉及若干树和二叉树的概念，如需查看，请点击链接跳转。

想要学会二叉树？树的概念与结构是必须要掌握的！快进来看看吧 http://t.csdn.cn/GWQJy

1.什么是堆？

堆是一种完全二叉树。只不过堆是二叉树顺序结构的实现，说白了就是将一个数组看作二叉树。也就是说，堆的逻辑结构是一棵二叉树，存储结构是数组。

堆又分为大堆和小堆：

大堆：树中所有父亲都大于等于孩子；

小堆：树中所有父亲都小于等于孩子。

注意，不满足这两点的二叉树不能称为堆（这点很重要）。

​

2.堆的实现

2.1 堆的结构定义

typedef int HPDataType;

typedef struct Heap
{
	HPDataType* a;  //存储数据
	int size;		//堆有效数据的大小
	int capacity;	//堆的容量
}Heap;

上文讲到，堆其实就是二叉树的顺序结构实现，所以用一个数组来存储数据。

2.2 函数声明

//给出一个数组，对它进行建堆
void HeapCreate(Heap* php, HPDataType* a, int n);
//堆的初始化
void HeapInit(Heap* php);
//对申请的内存释放
void HeapDestroy(Heap* php);
//添加数据
void HeapPush(Heap* php, HPDataType data);
//删除数据
void HeapPop(Heap* php);
//向上调整算法
void AdjustUp(HPDataType* a, int child);
//向下调整算法
void AdjustDown(HPDataType* a, int n, int parent);
//打印堆的数据
void HeapPrint(Heap* php);
//判断堆是否为空
bool HeapEmpty(Heap* php);
//返回堆的大小
int HeapSize(Heap* php);
//返回堆顶的数据
HPDataType HeapTop(Heap* php);
//交换函数
void Swap(HPDataType* p1, HPDataType* p2);

2.3 函数实现

由于堆的实现所用函数较多，这里就挑其中最难也是最重要的进行说明。

2.3.1 AdjustUp（向上调整算法）

当我们要实现在HeapPush（堆中添加数据data时），我们的做法是先将data插入到堆的尾部，再将data进行向上调整，直到它到达合适的位置。

如图，假设现在要将data=60添加到下面这个大堆中。

​

第一步，将60插入到堆的末尾，即数组的末尾。

​

第二步，比较60与它父亲节点的大小。因为要保证插入数据之后堆仍然是大堆，所以如果60大于父亲，则交换位置。

​

第三步，继续比较60与父亲的值，若大于父亲则交换位置。

​

至此，60已经到它正确的位置上了。

以上就是向上调整的过程，来看看代码实现。

void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;

	while (child > 0)
	{
		//建大堆用'>'，小堆用'<'
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

void HeapPush(Heap* php, HPDataType data)
{
	assert(php);
	//如果容量不足就扩容
	if (php->size == php->capacity)
	{
		int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType)*newCapacity);

		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		php->a = tmp;
		php->capacity = newCapacity;
	}
	//添加数据
	php->a[php->size] = data;
	php->size++;
	//将新入堆的data进行向上调整
	AdjustUp(php->a, php->size-1);
}

2.3.2 AdjustDown（向下调整算法）

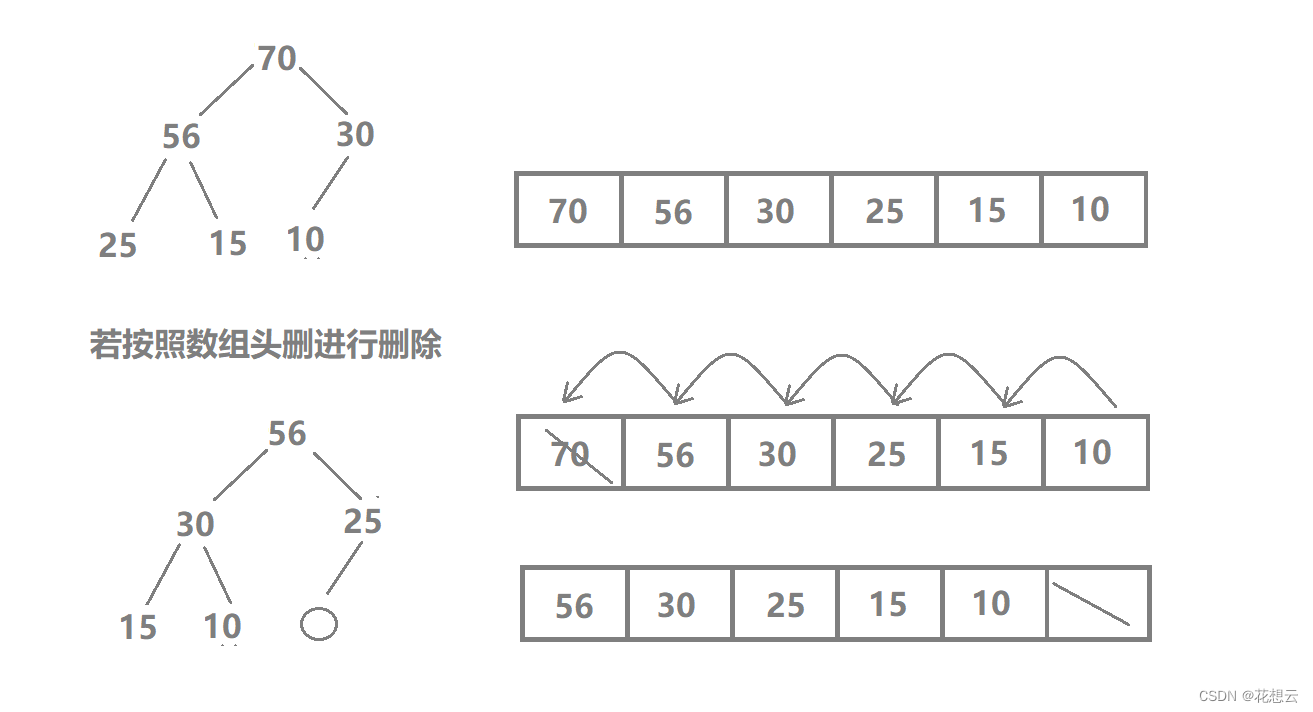
当我们要实现HeapPop（删除堆顶的数据）时，我们不能像往常的数组那样进行头删。因为数组再进行头删时，还要将从第二个位置起的后面的所有元素都向前平移。

但是堆这样行不通，因为随意挪动数据会造成关系的混乱。例如：

​

此时这个二叉树结构就不再是一个大堆了。

那么有什么好的办法不使堆的结构紊乱呢？这就得用到向下调整算法了。

例如，假设此时要删除堆顶的数据：​

第一步，交换堆顶与堆尾的值，并将堆的Size--（相当于删除了末尾的元素）。

​

第二步，对45进行向下调整。找出45的两个孩子中值最大（是小堆就选小的）的那个，如果5小于该数字就与其进行交换。

​

循环此步骤，直至45到达正确的位置。

显然，此时情况较为简单，只用一步就到达了正确位置。（此时70已经不存在了，所以不用比较）

以上就是向下调整的过程，来看看代码的实现。

void AdjustDown(HPDataType* a, int n, int parent)
{
	assert(a);
	//先默认较大的为左孩子
	int child = parent * 2+1;
	while (child<n)
	{
		//如果右孩子比左孩子大，就++
		if (a[child] < a[child + 1] && child + 1 < n)
		{
			child++;
		}
		//建大堆用'>'，小堆用'<'
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapPop(Heap* php)
{
	assert(php);
	assert(php->size>0);

	//将堆顶的数据与堆尾交换
	Swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;
	//将此时堆顶的data向下调整
	AdjustDown(php->a, php->size, 0);
}

特别注意：不管是向上调整还是向下调整，它们都得满足一个前提->

向上调整：进行向上调整的时候，该位置之前的所有数据已经是一个堆了。

向下调整：进行向下调整的时候，该位置的左子树和右子树都已经是堆了。

2.3.3 HeapCreate（如何建堆）

此函数所实现的功能是给出一个数组，对数组进行建堆（建大堆或者小堆）。

先来看看代码实现：

void HeapCreate(Heap* php, HPDataType* a, int n)
{
	php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);
	if (php->a == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	//将数组的内容全部拷贝到php->a中
	memcpy(php->a, a, sizeof(HPDataType) * n);
	php->size = php->capacity = n;

	//建堆算法
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(php->a, n, i);
	}
}

这里采用向下调整算法的的思路是，既然向下调整和向上调整都是有前提的，就不能直接进行使用。但是我们发现即使这个二叉树的数据是紊乱的，但是总有可以当作堆的一部分来使用向下调整（不用向上调整是因为不好控制）。例如：

​

在这个堆的底部（3个黑色圆圈里的部分）可以看作是堆，可以满足进行向下调整的条件。当把底层的三个堆建好以后，我们发现两个红色圆圈中的部分又可以看作满足条件的堆，对这两部分在进行向下调整。

​

完成之后，我们发现堆顶元素的左子树和右子树都已经是堆了，最后再将堆顶的元素进行向下调整，就建好一个完整的堆了。

总结起来就是如下图的步骤：

​

2.3.4 建堆的时间复杂度

因为堆是完全二叉树，而满二叉树也是完全二叉树，此处为了简化使用满二叉树来证明(时间复杂度本来看的就是近似值，多几个节点不影响最终结果)：

​

因此，建堆的时间复杂度为O(N)。

3. 完整源码

Heap.h文件

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<string.h>
#include<stdbool.h>

typedef int HPDataType;

typedef struct Heap
{
	HPDataType* a;   //存储数据
	int size;				//堆有效数据的大小
	int capacity;			//堆的容量
}Heap;

//给出一个数组，对它进行建堆
void HeapCreate(Heap* php, HPDataType* a, int n);
//堆的初始化
void HeapInit(Heap* php);
//对申请的内存释放
void HeapDestroy(Heap* php);
//添加数据
void HeapPush(Heap* php, HPDataType data);
//删除数据
void HeapPop(Heap* php);
//向上调整算法
void AdjustUp(HPDataType* a, int child);
//向下调整算法
void AdjustDown(HPDataType* a, int n, int parent);
//打印堆的数据
void HeapPrint(Heap* php);
//判断堆是否为空
bool HeapEmpty(Heap* php);
//返回堆的大小
int HeapSize(Heap* php);
//返回堆顶的数据
HPDataType HeapTop(Heap* php);
//交换函数
void Swap(HPDataType* p1, HPDataType* p2);

Heap.c文件 

#define _CRT_SECURE_NO_DEPRECATE 1
#include"Heap.h"

void HeapCreate(Heap* php, HPDataType* a, int n)
{
	php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);
	if (php->a == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	//将数组的内容全部拷贝到堆中
	memcpy(php->a, a, sizeof(HPDataType) * n);
	php->size = php->capacity = n;

	//建堆算法
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(php->a, n, i);
	}
}

void HeapInit(Heap* php)
{
	assert(php);

	php->a = NULL;
	php->size = php->capacity = 0;
}

void HeapPrint(Heap* php)
{
	assert(php);

	for (int i = 0; i < php->size; i++)
	{
		printf("%d ", php->a[i]);
	}
}

void HeapDestroy(Heap* php)
{
	assert(php);

	free(php->a);
	php->a = NULL;
	php->capacity = php->size = 0;
}

void HeapPush(Heap* php, HPDataType data)
{
	assert(php);
	//如果容量不足就扩容
	if (php->size == php->capacity)
	{
		int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType)*newCapacity);

		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		php->a = tmp;
		php->capacity = newCapacity;
	}
	//添加数据
	php->a[php->size] = data;
	php->size++;
	//将新入堆的data进行向上调整
	AdjustUp(php->a, php->size-1);
}

void HeapPop(Heap* php)
{
	assert(php);
	assert(php->size>0);

	//将堆顶的数据与堆尾交换
	Swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;
	//将此时堆顶的data向下调整
	AdjustDown(php->a, php->size, 0);
}

void AdjustDown(HPDataType* a, int n, int parent)
{
	assert(a);
	//先默认较大的为左孩子
	int child = parent * 2+1;
	while (child<n)
	{
		//如果右孩子比左孩子大，就++
		if (a[child] < a[child + 1] && child + 1 < n)
		{
			child++;
		}
		//建大堆用'>'，小堆用'<'
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;

	while (child > 0)
	{
		//建大堆用'>'，小堆用'<'
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

HPDataType HeapTop(Heap* php)
{
	assert(php);
	assert(php->size>0);

	return php->a[0];
}

int HeapSize(Heap* php)
{
	assert(php);

	return php->size;
}

bool HeapEmpty(Heap* php)
{
	assert(php);

	return !php->size;
}

void Swap(HPDataType* p1, HPDataType* p2)
{
	HPDataType tmp = *(p1);
	*(p1) = *(p2);
	*(p2) = tmp;
}

Test.c文件 

#define _CRT_SECURE_NO_DEPRECATE 1

#include"Heap.h"

void test()
{
	HPDataType arr[10] = { 12,34,45,78,56,74,3,7,9,5 };
	Heap hp;
	HeapCreate(&hp, arr, 10);
	//HeapInit(&hp);
	//HeapPush(&hp, 10);
	//HeapPush(&hp, 70);
	//HeapPush(&hp, 15);
	//HeapPush(&hp, 30);
	//HeapPush(&hp, 25);
	//HeapPrint(&hp);
	//HeapPop(&hp);
	//HeapPrint(&hp);
	//HeapPop(&hp);
	//HeapPrint(&hp);
	//HeapPop(&hp);
	HeapPrint(&hp);
}
int main()
{
	test();
	return 0;
}

至此，本章的内容就结束了，下一章将进行堆的实际应用——堆排序以及TopK问题的说明。

​

【版权声明】本文为华为云社区用户原创内容，转载时必须标注文章的来源（华为云社区）、文章链接、文章作者等基本信息， 否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱： cloudbbs@huaweicloud.com
二叉树 数据结构
  • 点赞
  • 收藏
  • 关注作者

评论（0）

0/1000
抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认 取消

加入云驻计划，成为创作者

  • 华为云周边好礼
  • 免费体验产品
  • 特殊身份标识
  • 线下官方门票
  • 内部专家零距离
  • 与10000+优质创作者共同成长
立即加入